안녕하세요. 오늘은 ICCV2021에 억셉된 Multiscale Vision Transformers (MViT)에 대해서 소개하도록 하겠습니다.
Multiscale Vision Transformers
We present Multiscale Vision Transformers (MViT) for video and image recognition, by connecting the seminal idea of multiscale feature hierarchies with transformer models. Multiscale Transformers have several channel-resolution scale stages. Starting from
arxiv.org
Background
최근 몇 년 동안 컴퓨터 비전 분야에서는 컨볼루션 신경망(Convolutional Neural Networks, CNN)이 주목받아 왔습니다. CNN은 사람의 시각 피질에서 영감을 받아 개발된 구조로, 이미지와 비디오에서 계층적이고 단계적으로 특징을 추출하는 데 뛰어난 성능을 보였습니다. 간단히 설명하면, CNN의 초기 레이어는 주로 이미지의 가장 간단한 패턴(예: 선, 모서리)을 높은 해상도에서 학습하고, 뒤쪽의 깊은 레이어로 갈수록 더 복잡한 패턴(예: 사물의 형태, 색상, 얼굴 등)을 낮은 해상도에서 학습합니다. 이러한 구조는 인간의 시각 처리 과정(V1→V4→IT)을 잘 따라가는 방식입니다.
**V1 (일차 시각피질): 기본적인 시각 특징 처리; V4 (중간 시각 영역): 형태 및 색상 처리; IT (하측두피질): 복잡한 물체 인식
최근 들어 자연어 처리(NLP)를 위해 개발된 트랜스포머(Transformer) 구조가 컴퓨터 비전에도 활용되기 시작했습니다. 대표적인 예가 Vision Transformer(ViT), Data-efficient Image Transformer(DeiT)입니다. 트랜스포머는 전역적인 자기 주의(global self-attention) 방식을 통해 데이터 내의 멀리 떨어진 관계를 효과적으로 학습합니다. 하지만 기존 트랜스포머 모델은 대규모 데이터셋을 활용한 사전 학습을 필요로 하고, 연산량도 매우 커서 실제로 사용하기에 부담이 컸습니다. 게다가 초기 트랜스포머 모델은 CNN과 달리 다양한 크기의 특징을 동시에 처리하는 다중 스케일(multi-scale) 처리가 어려운 단점이 있었습니다.
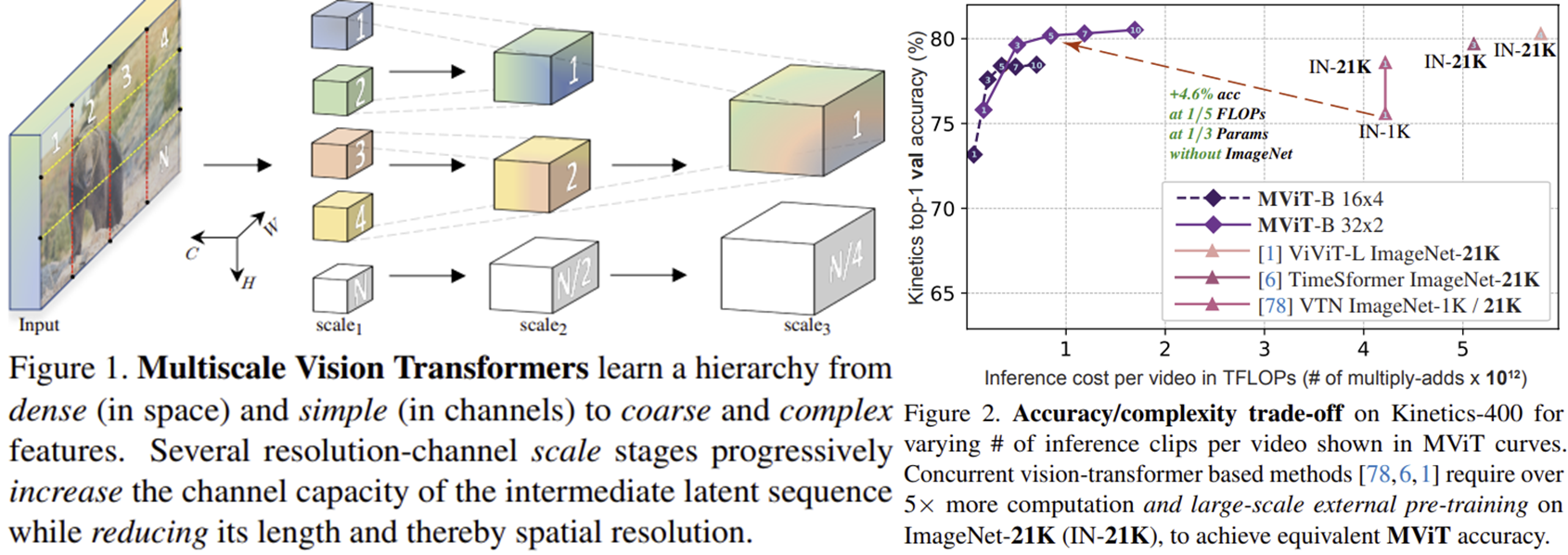
이러한 문제를 해결하기 위해 최근에는 트랜스포머 모델에 다중 스케일 특징을 효율적으로 처리할 수 있도록 통합한 멀티스케일 비전 트랜스포머(Multiscale Vision Transformer, MViT)가 개발되었습니다 (그림 1 참조). 특히, MViT는 "멀티헤드 풀링 어텐션(Multi-Head Pooling Attention, MHPA)"이라는 새로운 메커니즘을 도입하여 계산량을 크게 줄였습니다 (그림 2 참조). 이를 통해 MViT는 적은 연산량과 파라미터로도 이미지 및 비디오 인식 성능에서 뛰어난 결과를 보여주었습니다. 본 논문의 기여를 요약하면 다음과 같습니다.
- 멀티스케일 특징을 효과적으로 처리할 수 있는 멀티스케일 비전 트랜스포머(MViT) 구조 제안
- 계산량을 크게 줄이는 멀티헤드 풀링 어텐션(Multi-Head Pooling Attention, MHPA) 메커니즘 설계
- 기존 방법보다 적은 연산량과 파라미터로 이미지 및 비디오 인식 성능에서 우수한 결과 달성
Proposed Method: Multiscale Vision Transformer (MViT)
1) Multi-Head Pooling Attention (MHPA)
Motivation: 기존의 트랜스포머는 전역적인 자기 주의를 활용하여 모든 요소 간의 관계를 학습하지만, 이 방식은 계산 복잡도가 높아 비디오나 고해상도 이미지와 같은 데이터에 적용하기 어렵습니다. 이러한 문제를 해결하고 효율성을 높이기 위해 MHPA가 제안되었습니다.
Key Idea: 이를 위해 MHPA는 풀링 연산을 Query(Q), Key(K), Value(V)에 개별적으로 적용하여 입력 시퀀스의 길이를 감소시킵니다. 이를 통해 기존 트랜스포머에서 수행되는 자기 주의의 높은 연산 복잡도를 효과적으로 낮추고, 공간적·시간적 정보를 계층적으로 다룰 수 있게 합니다.
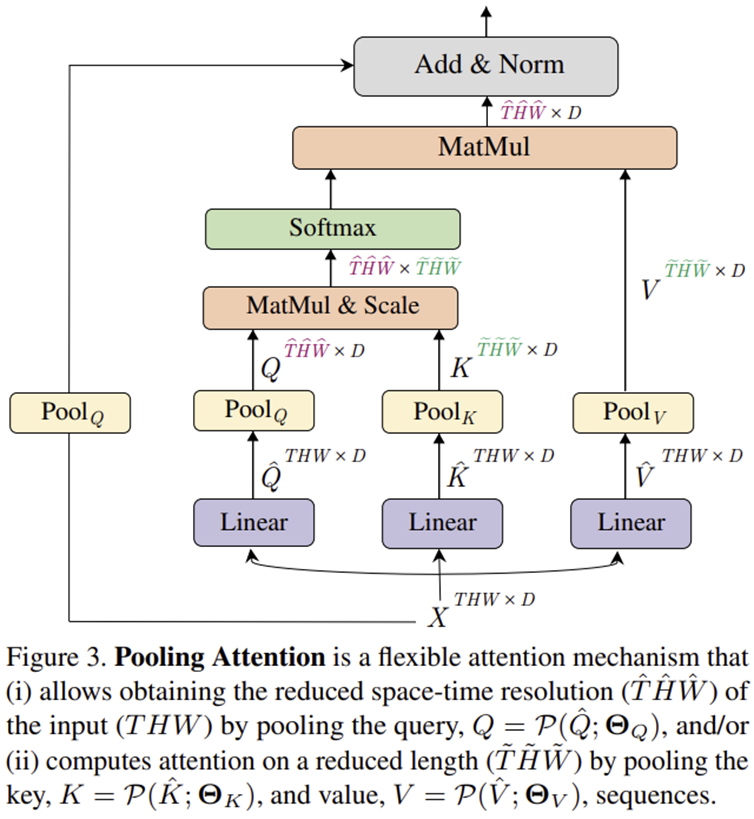
1-2) 풀링 연산(Pooling Operation)과 풀링 어텐션(Pooling Attention)
멀티헤드 풀링 어텐션(MHPA)에서 사용되는 풀링 연산(Pooling Operation)은 입력된 텐서(다차원 배열)를 특정 규칙에 따라 축소시키는 연산입니다. 이 연산을 정의하는 요소는 다음과 같습니다.
- Pooling Kernel Size (풀링 커널 크기) $\mathbf{k} \in \mathbb{R}^{k_{T} \times k_{H} \times k_{W}}$: 풀링을 할 때 한 번에 처리할 데이터의 크기를 나타냅니다.
- Pooling Stride Size (풀링 스트라이드 크기) $\mathbf{s} \in \mathbb{R}^{s_{T} \times s_{H} \times s_{W}}$: 커널이 데이터를 이동할 때 이동하는 간격을 나타냅니다.
- Pooling Padding Size ( 풀링 패딩 크기 ) $\mathbf{p} \in \mathbb{R}^{p_{T} \times p_{H} \times p_{W}}$: 입력 데이터의 경계를 처리하기 위해 추가되는 패딩의 크기 의미합니다.
이 세 가지 요소를 통해 입력 텐서 $\mathbf{L}$ 는 풀링 연산 후 다음과 같은 형태로 출력됩니다.
$$\tilde{\mathbf{L}} = \lfloor \frac{\mathbf{L} + 2\mathbf{p} - \mathbf{k}}{\mathbf{s}} \rfloor + 1$$
여기서 $\lfloor \cdot \rfloor$는 소수점 이하를 버리고 정수 부분만 남기는 연산을 의미합니다. 마지막으로, 풀링 연산이 끝난 후 결과로 얻은 텐서를 일차원으로 펼쳐(flattening), 시퀀스 길이 $\tilde{T} \times \tilde{H} \times \tilde{W}$ 와 hidden dimension $D$ 가진 형태 ($\tilde{T} \times D$) 로 변환하게 됩니다. 이렇게 얻어진 텐서는 자기 주의 연산(self-attention)에 사용되어 다양한 스케일의 시공간적 특징을 효과적으로 학습할 수 있게 합니다. 풀링된 특징맵을 이용해서 흔히 저희가 지금까지 해왔던 자기주의 매커니즘을 적용합니다.
이 과정을 step-by-step으로 요약하면 다음과 같습니다.
STEP1. Q(Query), K(Key), V(Value) 벡터를 초기 텐서에서 각각 추출합니다.
STEP2. 각 텐서(Q, K, V)에 독립적으로 풀링 연산을 적용하여 시퀀스 길이를 줄입니다.
STEP3. 풀링된 결과를 기반으로 축소된 시퀀스 길이를 가진 새로운 텐서를 얻습니다.
STEP4. 축소된 시퀀스를 이용해 자기 주의 연산을 수행하며, 수식적으로는 아래와 같이 표현됩니다:
$$\text{Attention} (Q, K, V) = \text{Softmax} (\frac{QK^{T}}{\sqrt{D}})V = \text{Softmax} (\frac{\mathcal{P}(\hat{Q}; \Theta_{Q}) \mathcal{P}(\hat{K}; \Theta_{K})}{\sqrt{D}}) \mathcal{P} (\hat{V}; \Theta_{V})$$
STEP5. 멀티헤드 구조로 확장되어 병렬적으로 연산됩니다. 각 헤드는 입력 텐서의 채널을 서로 겹치지 않게 나누어 독립적으로 어텐션 연산을 수행하며, 병렬 계산을 통해 효율성을 극대화합니다.
Computational Analysis: 트랜스포머 구조는 자기 주의 연산(self-attention)이 입력 시퀀스 길이에 따라 연산량이 제곱으로 증가하는 특성이 있어 계산 부담이 매우 큽니다. 여기서 Multi-Head Pooling Attention(MHPA)은 Q, K, V 텐서에 풀링 연산을 적용하여 시퀀스 길이를 효과적으로 줄입니다. MHPA를 수행 시 각 텐서의 시퀀스 길이는 풀링의 스트라이드 길이를 곱한 값으로 감소됩니다. 즉 $j \in \{ Q, K, V \}$라고 할 때 다음과 같이 표현할 수 있죠.
$$f_{j} = s^{j}_{T} \cdot s^{j}_{H} \cdot s^{j}_{W} $$
이제 MHPA의 입력 텐서가 $D \times T \times H \times W$의 차원을 가진다고 가정하면, MHPA의 시간 복잡도(run-time complexity)는 헤드(head) 하나당 다음과 같이 나타납니다
$$\mathcal{O} (\frac{THWD}{h} ( D + \frac{THW}{f_{Q}f_{K}} ))$$
또한 메모리 복잡도(memory complexity)는 다음과 같습니다:
$$\mathcal{O} (THWh ( \frac{D}{h} + \frac{THW}{f_{Q}f_{K}} ))$$
이러한 계산량과 메모리 사용량은 채널 수 $D$ 와 시퀀스 길이 $THW$ 간의 상호관계에 따라 결정됩니다. 따라서 채널 수와 헤드의 수, 레이어의 너비와 같은 다양한 구조적 파라미터를 설계할 때 이 상충관계를 고려하여 최적화해야 합니다. MHPA는 이를 통해 트랜스포머 모델의 연산 효율성을 극대화할 수 있습니다.
2) Multiscale Transformer Networks
2-1) Preliminaries: Vision Transformers (ViT)
STEP1. 입력 영상(해상도: $T \times H \times W$)을 겹치지 않는 크기 $1 \times 16 \times 16$의 패치(patch)로 나눕니다.
STEP2. 나누어진 이미지 패치를 1차원으로 펼친 후, 이를 hidden dimension $D$로 변환하기 위해 선형 레이어를 적용합니다.
STEP3. 위치 정보를 나타내는 포지셔널 임베딩(Positional embedding, $\mathbf{E} \in \mathbb{R}^{L \times D}$)을 각 이미지 패치에 추가합니다.
STEP4. 학습 가능한 클래스 임베딩(Class embedding)을 이미지 패치에 덧붙입니다
STEP5. 변환된 패치 시퀀스에 다중 헤드 자기 주의(Multi-Head Self-Attention, MHSA)와 다층 퍼셉트론(MLP)을 적용합니다.
STEP6. 마지막으로 선형 레이어를 통과시켜 최종적으로 원하는 출력 값을 예측합니다.
2-2) Multiscale Vision Transformers (MViT)

MViT는 다중 스케일(multiscale) 특징을 효율적으로 처리하기 위해 고안된 트랜스포머 모델입니다. 초기 레이어에서는 높은 시공간 해상도와 상대적으로 낮은 채널 수로 구성된 미세한 정보를 처리합니다. 이후 단계가 진행될수록 시공간 해상도는 점진적으로 감소시키고 채널의 수는 증가시켜 고차원적이고 복잡한 특징을 추출할 수 있도록 설계되었습니다. 특히 각 단계에서 MHPA를 적용하여 해상도를 조절하고, 계산량과 메모리를 효율적으로 관리하여 성능과 효율성을 동시에 높일 수 있습니다. 이와 같은 구조적 특징은 이미지 및 비디오 데이터에서 다양한 크기의 시각적 특징을 효과적으로 다룰 수 있도록 합니다. 표 1과 표 2는 각각 ViT와 MViT의 각 단계 별 해상도의 차이를 보여주고 있습니다.
Experiment Results
1) Video Recognition


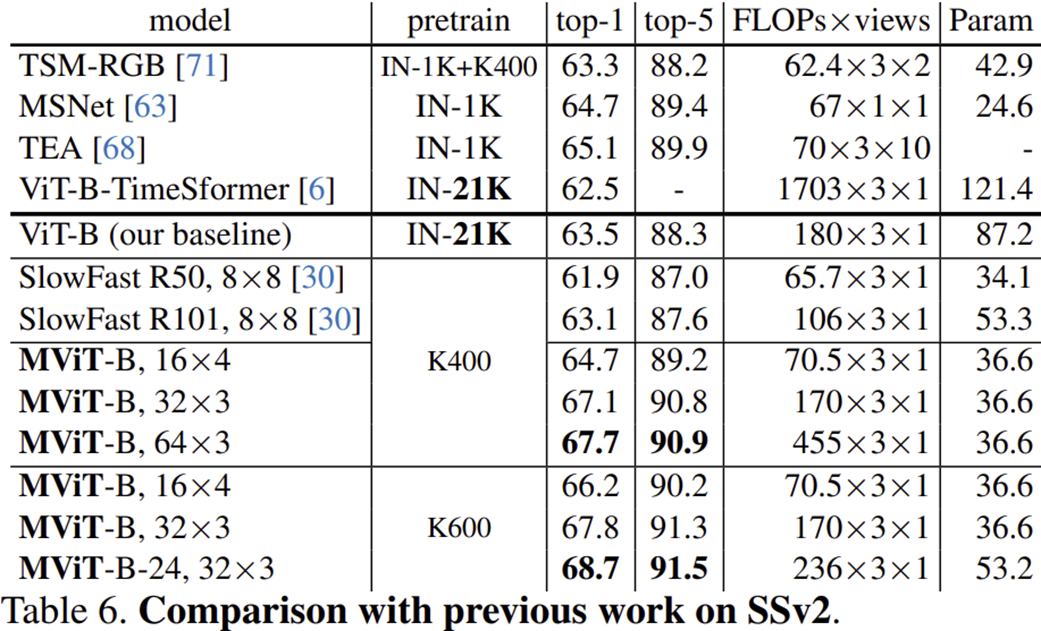


2) Ablation Study
2-1) Shuffling frames in inference

- MViT-B 모델은 입력 비디오 프레임의 시간적 순서를 임의로 섞었을 때, 정확도가 크게 감소했습니다(77.2% → 70.1%, -7.1% 하락).
- 반면, 기존의 ViT-B 모델은 프레임을 섞었을 때 정확도가 거의 변하지 않았습니다(68.5% → 68.4%, 단지 -0.1% 하락).
- 이는 MViT가 비디오 내의 시간적 정보를 적극적으로 활용하고 있음을 나타내며, ViT는 시간적 정보를 무시하고 있음을 시사합니다.
2-2) Query (scale stage) and Key-Value pooling on ViT-B
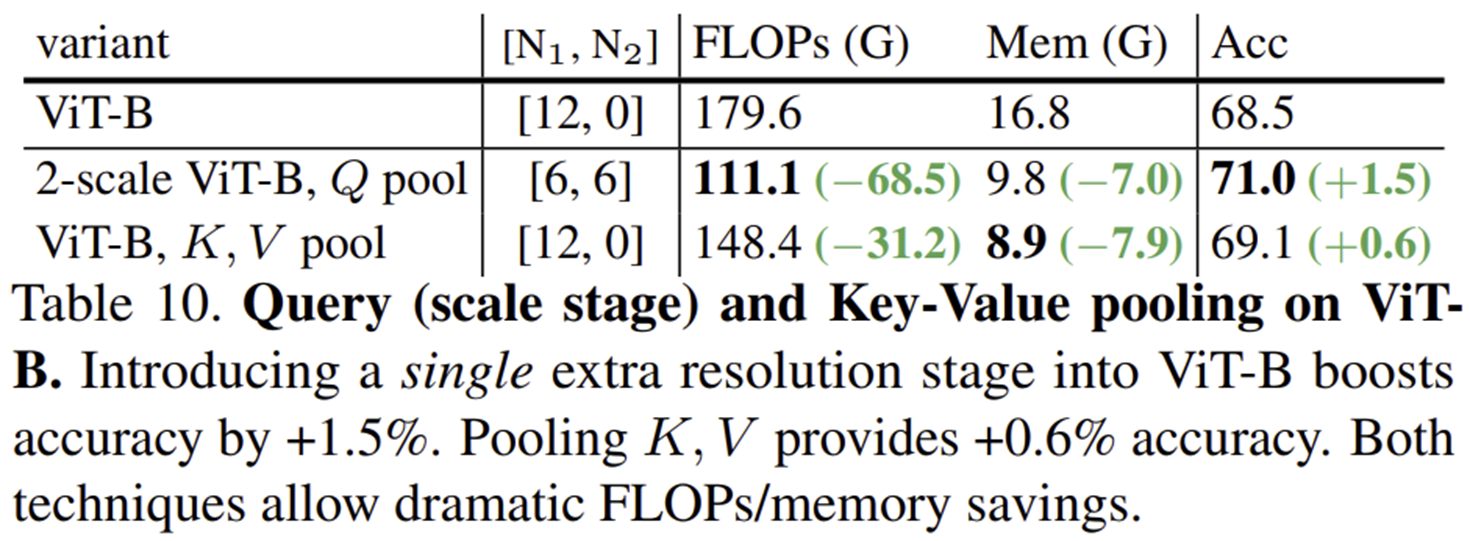
- 기본 ViT-B 모델과 비교하여 두 가지 변형된 구조를 실험했습니다:
- 2-scale ViT-B (Query 풀링 적용): 연산량(FLOPs)이 68.5G 감소하고, 메모리 사용량은 7.0G 감소했으며, 정확도는 1.5% 상승했습니다.
- ViT-B (Key-Value 풀링 적용): 연산량이 31.2G 감소하고 메모리 사용량이 7.9G 감소했으며, 정확도는 0.6% 상승했습니다.
- 위 결과는 ViT-B 모델에 단 하나의 추가적인 스케일 단계를 추가하거나 Key, Value 풀링만 적용해도 정확도 향상과 함께 연산량 및 메모리를 상당히 절약할 수 있음을 나타냅니다. 특히 Query 풀링을 추가한 다중 스케일 구조가 성능과 효율성 모두에서 가장 효과적임을 보여줍니다.
2-3) Space-time positional embedding
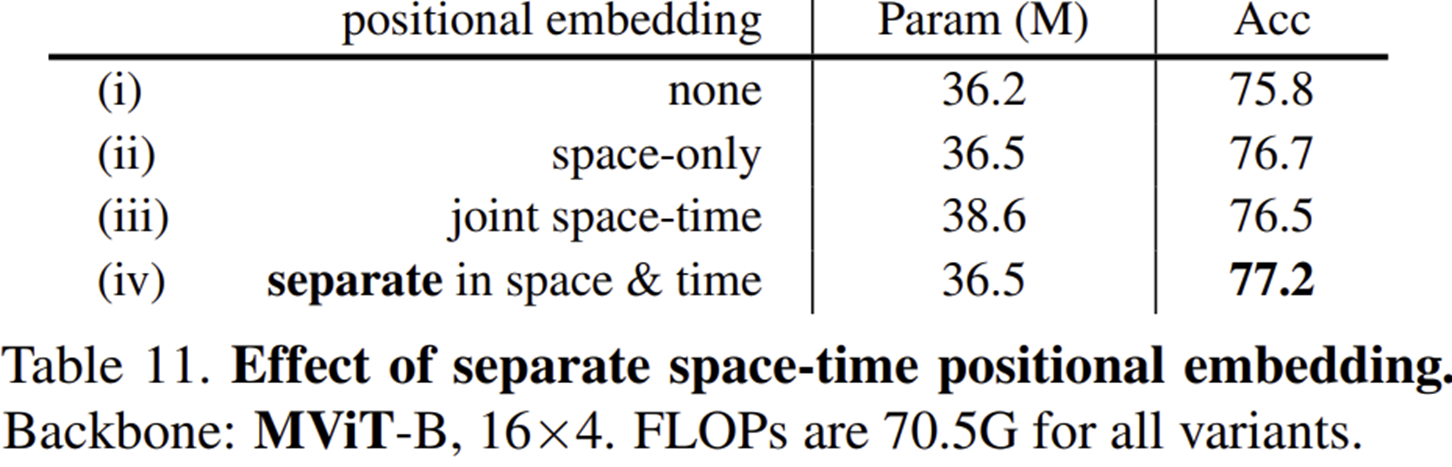
- MViT-B 모델에서 다양한 위치 임베딩 방법의 효과를 비교한 결과입니다.
- 공간과 시간 축을 따로 구분한(separate) 위치 임베딩 방법(iv)이 가장 높은 정확도(77.2%)를 기록했습니다.
- 공간만을 고려한 위치 임베딩(ii) 또한 높은 정확도(76.7%)를 보였으나, 시공간을 함께(joint space-time) 고려한 위치 임베딩(iii)은 정확도가 다소 감소(76.5%)했습니다.
- 위치 임베딩을 전혀 사용하지 않은 경우(i)에는 정확도가 가장 낮았습니다(75.8%).
즉, 시공간적 정보를 따로 구분하여 임베딩하는 방식이 가장 효과적인 방법임을 확인할 수 있습니다.
2-4) Input sampling

- 입력 샘플링 방식에 따라 다양한 시공간 큐브(space-time cube)의 크기와 스트라이드를 실험했습니다.
- 시간적 차원이 1보다 클 때(3 또는 7), 시간 정보를 더 효과적으로 활용하여 정확도가 높아졌습니다.
- 특히, 32×2의 샘플링과 7×7×7 큐브 크기를 가진 방식이 가장 높은 정확도(77.3%)를 달성했습니다.
- 논문의 기본(default) 설정(밑줄 친 부분: 16×4, 큐브 크기 3×7×7, 스트라이드 2×4×4)도 높은 정확도(77.2%)를 보이며, 시간적 큐브 크기를 증가시키는 것이 성능 향상에 유리함을 보여줍니다.
- 전반적으로 공간 및 시간 해상도를 조정하면서도 연산량(FLOPs)과 파라미터(Param)는 거의 동일하게 유지되어 효율적인 성능 향상이 가능합니다.
2-5) Scale blocks
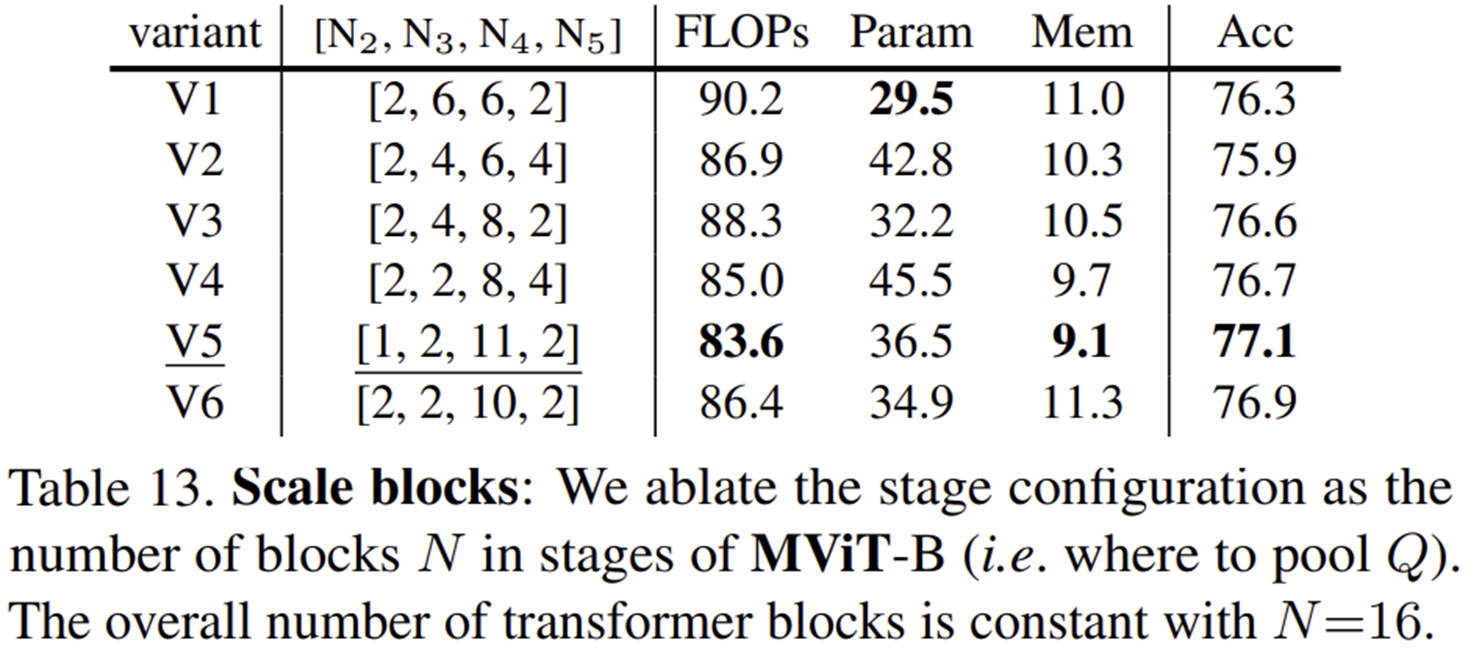
- MViT-B 모델에서 다양한 블록 구성을 통해 성능을 분석한 실험입니다.
- 모든 변형 모델은 Transformer 블록의 총 개수 ($N = 16$) 는 동일하게 유지하며, 각 스케일의 블록 개수 $[N_{2}, N_{3}, N_{4}, N_{5}]$ 를 다르게 구성했습니다.
- 가장 효율적인 구성(V5, [1, 2, 11, 2])은 가장 낮은 연산량(FLOPs: 83.6G)과 가장 적은 메모리 사용량(9.1G)으로도 가장 높은 정확도(77.1%)를 기록했습니다.
- 반면, 블록 개수가 균등하거나 초기 단계에 집중된 구성(V1, V2)은 상대적으로 정확도가 떨어지고 연산량과 메모리 사용량도 증가했습니다.
즉, 네트워크 깊은 단계에 많은 블록을 집중적으로 배치하는 것이 연산 효율성과 정확도를 모두 높이는 데 가장 효과적임을 보여줍니다.
2-6) Key-Value pooling

- Key와 Value에 적용된 풀링 방식에서 stride 크기 ($s = s_{T} \times s_{H} \times s_{W} $)와 adaptive 방식(해상도에 따라 stride를 조정하는 방식)의 효과를 비교한 실험입니다.
- stride를 사용하지 않을 경우 정확도가 가장 높았으나(77.6%), 연산량과 메모리 사용량이 매우 컸습니다(130.8G FLOPs, 16.3G 메모리).
- adaptive 방식을 적용한 경우(특히 2×4×4 stride)는 연산량(83.6G)과 메모리 사용량(9.1G)이 감소하면서도 상대적으로 높은 정확도(77.1%)를 유지하여 효율적임을 보였습니다.
- 가장 낮은 연산량(63.7G)과 메모리 사용량(6.3G)을 보인 adaptive 2×8×8 stride는 정확도 면에서는 다소 감소(75.8%)했습니다.
즉, adaptive stride를 사용하면 연산량과 메모리 사용량을 크게 절약하면서도 정확도의 감소를 최소화할 수 있습니다. 특히 2×4×4의 adaptive stride 설정이 성능과 효율성 간 균형이 뛰어난 것으로 나타났습니다.
2-7) Pooling function

- 여러 가지 풀링 함수(max pooling, average pooling, convolution pooling)와 다양한 커널 크기를 적용한 실험입니다.
- Convolution pooling이 가장 높은 성능을 보였으며, 특히 커널 크기가 고정된 3×3×3 convolution pooling이 가장 높은 정확도(78.4%)를 기록했습니다.
- max pooling과 average pooling은 convolution pooling 대비 상대적으로 낮은 성능을 보였으며, 특히 average pooling은 가장 낮은 정확도(75.4%)를 보였습니다.
- 풀링 커널 크기가 stride와 동일하거나 약간 클 때 (s 또는 s+1), max pooling이 준수한 성능(77.2%)을 나타내었으나, 커널이 너무 커지면 (2s+1) 성능이 오히려 떨어졌습니다.
결과적으로, 학습 가능한 채널별 convolution pooling 방식이 성능 향상에 가장 효과적이었으며, 적절한 커널 크기 설정이 중요함을 확인할 수 있습니다.
3) Efficiency Analysis
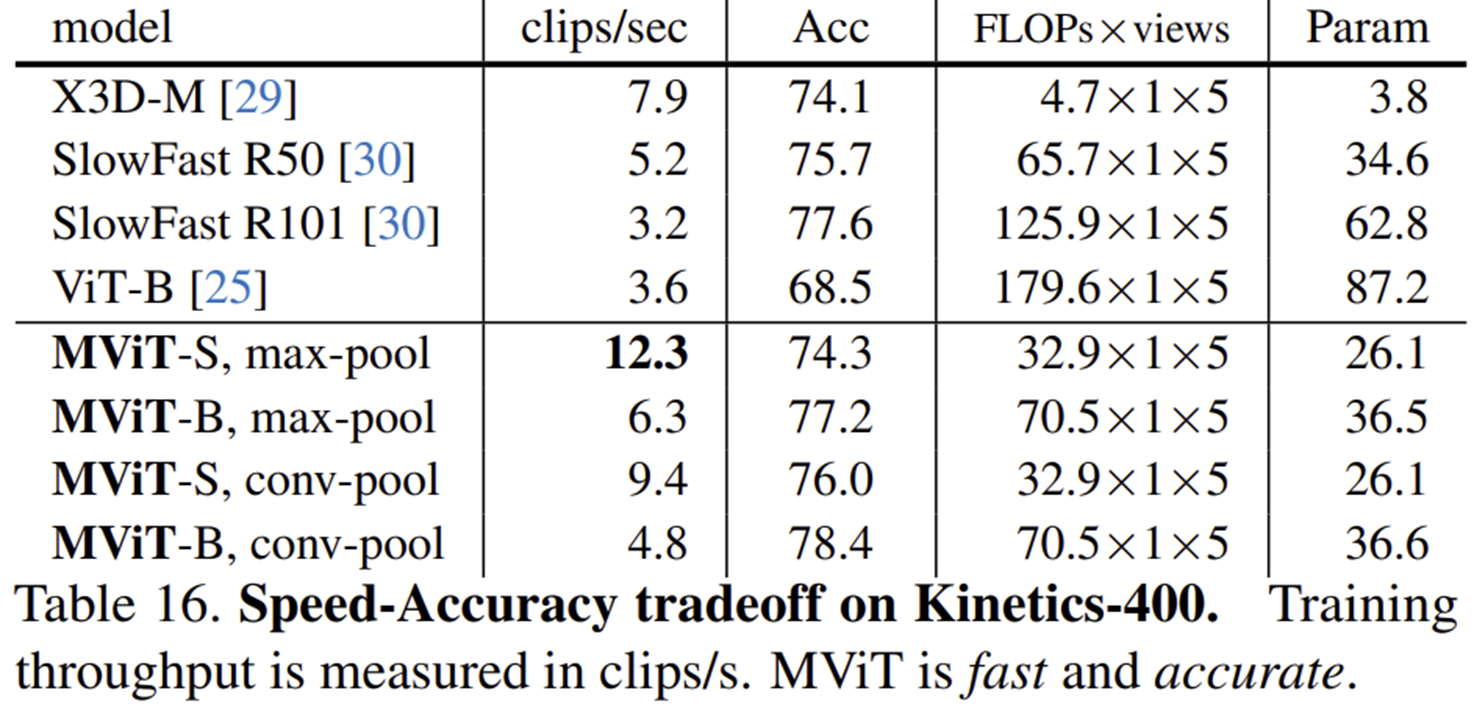
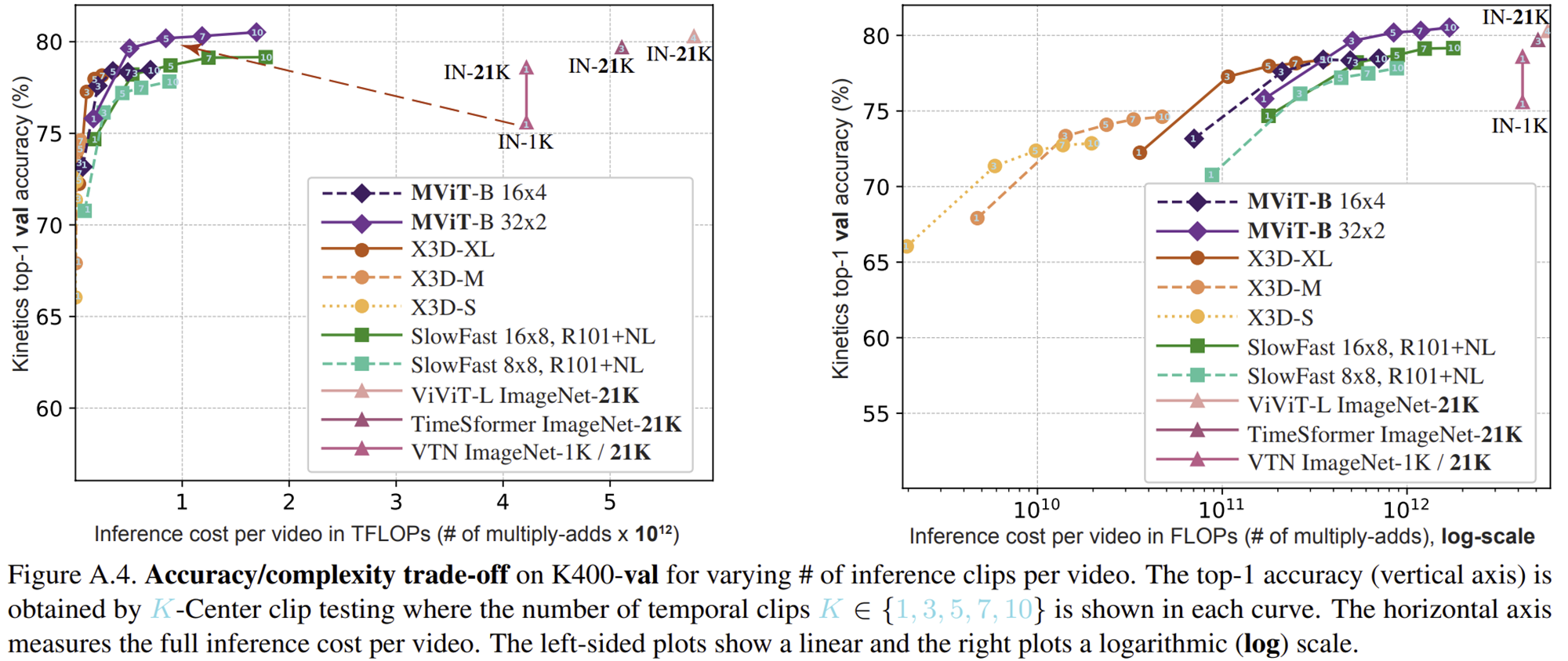
- Kinetics-400 데이터셋에서 비디오당 여러 개의 클립(clip)을 사용하여 테스트한 결과입니다.
- MViT-B 모델(16x4 및 32x2)은 기존의 대표적인 CNN 기반 모델들(X3D, SlowFast) 및 다른 Transformer 기반 모델들(ViViT, TimeSformer, VTN)과 비교하여 더 낮은 연산량(TFLOPs, 클립 당 연산량)으로 더 높은 정확도를 달성했습니다.
- 특히 MViT-B는 상대적으로 낮은 연산량으로도 빠르게 정확도가 상승하여 효율적인 성능을 보였으며, CNN 기반 모델인 X3D 및 SlowFast 대비 정확도와 효율성 모두에서 우수했습니다.
- 또한, ImageNet-21K와 같은 큰 데이터셋에서 사전 학습된 모델(ViViT-L, TimeSformer, VTN)보다도 연산 효율성 측면에서 우수한 성능을 나타냈습니다.
'Paper Review' 카테고리의 다른 글
| MISSFormer: An Effective Medical Image Segmentation Transformer (IEEE TMI2023) (0) | 2025.04.04 |
|---|---|
| Unet++: A Nested U-net Architecture for Medical Image Segmentation (DLMIA2018) (0) | 2025.04.01 |
| Segmenter: Transformer for Semantic Segmentation (ICCV2021) (0) | 2025.03.25 |
| Inception Transformer (NIPS2022) (0) | 2025.03.09 |
| Mobile-Former: Bridging MobileNet and Transformer (CVPR2022) (0) | 2025.02.10 |
