LocalViT: Analyzing Locality in Vision Transformers (arxiv2021)

안녕하세요. Transformer에서 사용하는 FFN이 최근 depth-wise separable convolution을 추가해서 많이 사용하고 있습니다. 오늘은 이를 처음으로 제시한 LocalViT에 대해서 소개하도록 하겠습니다. 

 

LocalViT: Analyzing Locality in Vision Transformers

 

 

Background

최근 몇 년간, 컴퓨터 비전 분야에서 Vision Transformer (ViT)는 뛰어난 성능을 나타내며 큰 주목을 받고 있습니다. CNN이 이미지 처리의 대표적인 아키텍처로 오랜 기간 동안 사용되었지만, Transformer 아키텍처가 이미지 분야로 확장되면서 이미지 분류 및 객체 탐지와 같은 다양한 작업에서 CNN과 비슷하거나 더 뛰어난 성능을 보여주었습니다.

 

하지만 ViT는 일반적으로 많은 양의 데이터로 사전 훈련을 필요로 하며, 작은 규모의 데이터셋에서는 성능이 떨어진다는 단점이 있습니다. 또한, CNN은 국지적(local) 정보를 활용하는 구조를 갖고 있는 반면, ViT는 전체 이미지에 대한 글로벌 어텐션(global attention) 메커니즘을 사용하기 때문에 이미지 내의 지역적 구조와 정보(locality)를 제대로 활용하지 못한다는 문제점이 제기되었습니다.

 

이러한 문제를 해결하기 위해 최근 연구들은 Transformer 아키텍처에 국지적 구조를 도입하는 다양한 방법들을 제안해왔습니다. 예를 들어, Swin Transformer, PVT, TNT 등은 Transformer의 효율성과 성능을 높이기 위해 다양한 local attention 메커니즘을 활용하였으며, 이를 통해 모델이 지역적 정보를 더 효과적으로 활용할 수 있게 하였습니다.

 

본 논문에서는 이러한 기존 연구에서의 국지적(local) 및 전역적(global) 정보 활용 방식을 분석하고, Transformer 구조 내에서 지역성(locality)이 어떤 역할을 하는지 체계적으로 탐구하는 연구를 수행했습니다. 이를 통해, ViT 구조에서 locality를 더욱 효과적으로 활용할 수 있는 설계 원리를 제시하고 있습니다. 본 논문의 기여도를 정리하면 다음과 같습니다. 

 

• 기존의 FFN을 sequence 관점과 lattice 관점으로 서로 다르게 해석하여 이를 MobileNet의 Inverted Residual Block과의 유사성을 기반으로 FFN에 locality를 주입할 수 있는 아주 쉬운 방법을 제시하였습니다. 
• Transformer의 구조 내에 locality를 명시적으로 도입한 다양한 변형 아키텍처(LocalViT)를 설계하고, 각 변형 모델의 성능을 여러 데이터셋과 작업에서 체계적으로 비교 및 평가하여 locality의 효과를 정량적으로 검증하였습니다.

 

 

Proposed Method: LocalViT

1) Input Interpretation

 

그림 2는 본 논문에서 FFN의 동작과정을 두가지로 해석할 수 있음을 보여주고 있습니다. (a)는 sequence 관점으로 해석한 것이고 (b)는 lattice (격자) 관점으로 해석하였습니다. 그럼 하나씩 살펴보도록 하겠습니다. 

 

1-1) Sequence Perspective

일반적으로 ViT를 컴퓨터 비전 분야에 적용할 때를 다시 떠올려보도록 하겠습니다. 일반적으로 입력 영상 $\mathbf{X} \in \mathbb{R}^{C \times H \times W}$이 주어지면 이를 패치로 나눈 뒤 각 패치를 토큰 $\{ \hat{\mathbf{X}}_{i} \in \mathbb{R}^{d} | i = 1, 2, \dots, N \}$으로 임베딩하는 과정이 들어가죠. 여기서 $d = C \times p^{2}$이고 $N = \frac{H}{p} \times \frac{W}{p}$로 각각 hidden dimension과 토큰의 개수로 정의됩니다. 

 

다음 단계는 각 토큰들을 query $\mathbf{Q}$, key $\mathbf{K}$, 그리고 value $\mathbf{V}$로 매핑한 뒤 self-attention을 적용합니다. 이 과정을 통해 모든 토큰, 즉 패치들 간의 상관성을 이해하여 global context information을 추출할 수 있는 것 이죠.

 

$$\mathbf{Z} = \text{Softmax} \left( \frac{\mathbf{Q}\mathbf{K}^{T}}{\sqrt{d}} \right) \mathbf{V}$$ 

 

여기서 $\mathbf{Q} = \hat{\mathbf{X}} \mathbf{W}_{Q}, \mathbf{K} = \hat{\mathbf{X}} \mathbf{W}_{K}, \mathbf{V} = \hat{\mathbf{X}} \mathbf{W}_{V}$로 얻을 수 있습니다. 그리고, 각 linear projection matrix $\mathbf{W}_{Q}, \mathbf{W}_{K}, \mathbf{W}_{V} \in \mathbb{R}^{R}^{d \times d}$로 정의됩니다. 마지막으로 두 개의 fully-connected layer로 구성된 Feed-Forward Network (FFN)에 입력되어 학습의 안정성을 향상시킵니다. 

 

$$\mathbf{Y} = f(\mathbf{Z} \mathbf{W}_{1}) \mathbf{W}_{2}$$

 

여기서 $\mathbf{W}_{1} \in \mathbb{R}^{d \times \gamma d}$ 그리고 $\mathbf{W}_{2} \in \mathbb{R}^{\gamma d \times d}$인 linear projection으로 정의되며 $\gamma$는 MLP의 expansion ratio입니다. 마지막으로 $f(\cdot)$는 non-linear activation function입니다. 

 

1-2) Lattice Perspective

지금까지는 sequence 관점에서 보았으니 이를 lattice, 즉 image의 관점에서 해석을 해보면 어떨까요? 이는 FFN을 수행하기 전에 sequence token을 image로 reshape만 해주면 됩니다. 즉, $\mathbf{Z} \in \mathbb{R}^{N \times d}$를 2D lattice $\mathbf{Z}^{r} \in \mathbb{R}^{h \times w \times d}$로 reshape하는 것이죠. 이 과정을 $\mathbf{Z}^{r} = \text{Seq2Img}(\mathbf{Z})$라고 표현하였으며 $h = \frac{H}{p}$ 그리고 $w = \frac{W}{p}$로 정의됩니다. 이를 통해 sequence 였던 토큰들이 기존의 위치정보를 되찾았으므로 token들 사이의 proximity 즉, locality를 추출할 수 있게 되었습니다. 따라서, 이를 $1 \times 1$ convolution으로 다음과 같이 수행할 수 있습니다. 

 

$$\begin{cases} &\mathbf{Y}^{r} = f(\mathbf{Z}^{r} * \mathbf{W}^{r}_{1}) * \mathbf{W}^{r}_{2} \\ &\mathbf{Y} = \text{Img2Seq}(\mathbf{Y}^{r}) \end{cases}$$

 

여기서 $\mathbf{W}^{r}_{1} \in \mathbb{R}^{d \times \gamma d \times 1 \times 1}$ 그리고 $\mathbf{W}^{r}_{2} \in \mathbb{R}^{\gamma d \times d \times 1 \times 1}$로 정의되며 이는 합성곱 연산의 커널로 활용됩니다. 그리고 다음 단계에서 self-attention 연산을 위해 다시 image에서 sequence로 변환하는 $\text{Img2Seq}(\cdot)$을 적용하는 것을 볼 수 있죠. 

 

2) Locality

 

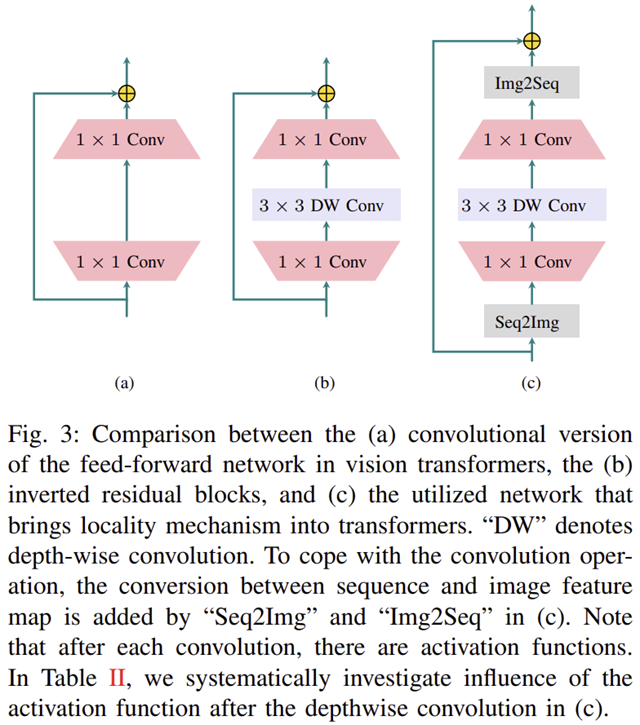
하지만 $1 \times 1$ 합성곱으로는 FFN에 locality를 충분히 주입할 수 없습니다. 이를 위해 본 논문에서 집중한 것인 MobileNet의 Inverted Residual Block입니다. 그림 3에서 (a)는 합성곱 기반의 FFN 그리고 (b)는 Inverted Residual Block을 보여주고 있습니다. 굉장히 구조적으로 유사한 것을 볼 수 있습니다. 오직 다른점은 중간에 $3 \times 3$ depth-wise convolution이기 때문에 이를 추가하여 최종적으로 그림 3 (c)와 같은 구조를 만들어주었습니다. 

 

3) Class Token

보통 Transformer 기반으로 image classification을 수행할 때는 class token이라는 learnable token을 하나 더 추가해주게 됩니다. 따라서, $\hat{\mathbf{X}} \leftarrow \text{Concat}(\mathbf{X}_{cls}, \hat{\mathbf{X}})$와 같이 되죠. 여기서, $\mathbf{X}_{cls} \in \mathbb{R}^{1 \times d}$로 class token을 의미합니다. 따라서, 새롭게 만들어지는 sequence는 $\hat{\mathbf{X}} \in \mathbb{R}^{(N + 1) \times d}$로 총 $N + 1$개의 토큰이 존재합니다. '

 

하지만, 이를 영상의 크기로 2D로 reshape하는 것은 불가능합니다. 따라서, 이를 해결하기 위해 FFN에 통과시키기 전에 class token을 따로 분리시켜줍니다.

 

$$(\mathbf{Z}_{cls}, \mathbf{Z}) \leftarrow \text{Split} (\mathbf{Z})$$

 

그리고 $\mathbf{Z}$만 FFN에 넣어서 $\mathbf{Y}$를 얻고 이를 다시 하나로 합쳐주는 것이죠 

 

$$\mathbf{Y} \leftarrow \text{Concat}(\mathbf{Z}_{cls}, \mathbf{Y})$$

 

Experimental Results

1) Ablation Study

1-1) Influence of the Locality

 

실험은 Vision Transformer(DeiT-T)에 지역성(locality)을 추가한 모델(LocalViT-T)의 성능을 평가하기 위한 것입니다. 특히 Depthwise Convolution과 활성화 함수(ReLU6)를 도입하여 locality 효과를 분석했습니다.

• Patch 크기(γ)가 4일 때:
  • 기존 모델(DeiT-T)의 Top-1 정확도는 72.2%였으나, locality를 추가한 모델(LocalViT-T)은 같은 파라미터 수(5.7M)로 정확도가 72.5%(+0.3%)로 소폭 향상되었습니다.
  • Depthwise Convolution과 ReLU6 활성화를 추가한 모델(LocalViT-T*)은 파라미터 수가 조금 증가(5.8M)하면서 정확도가 73.7%(+1.5%)로 더 뚜렷하게 증가했습니다.
• Patch 크기(γ)가 6일 때:
  • DeiT-T의 정확도는 73.1%였으며, locality를 도입한 LocalViT-T는 같은 파라미터 수(7.5M)에서 정확도가 74.3%(+1.2%)로 향상되었습니다.
  • Depthwise Convolution과 ReLU6 활성화를 적용한 LocalViT-T*는 파라미터가 7.7M으로 약간 늘어났지만, 정확도가 76.1%(+3.0%)로 상당히 크게 개선되었습니다.

결론적으로, 이 실험은 Depthwise Convolution을 활용하여 Vision Transformer에 locality를 추가하는 것이 모델 성능을 뚜렷하게 향상시킬 수 있음을 보여줍니다. 특히 Depthwise Convolution과 ReLU6 활성화의 결합이 가장 큰 성능 향상을 이끌어낸다는 점을 명확하게 확인할 수 있습니다.

 

1-2) Activation Functions

 

이 실험은 Vision Transformer (DeiT-T 모델)에 다양한 비선형 활성화 함수(Non-linear activation function)와 채널 어텐션 메커니즘(SE, ECA)을 적용했을 때 성능 변화를 비교한 것입니다. (Patch 크기(γ)는 4로 고정)

• 기존 DeiT-T 모델의 Top-1 정확도는 72.2% (5.7M) 입니다.
• 활성화 함수를 ReLU6로 바꿀 경우 정확도가 73.7%(+1.5%)로 증가했습니다(5.8M).
• h-swish(HS) 활성화를 사용할 경우 정확도는 74.4%(+2.2%)로 더욱 향상되었습니다(5.8M).
• HS 활성화에 추가로 ECA (Efficient Channel Attention) 모듈을 적용하면, 성능이 74.5%(+2.3%)로 소폭 개선되었습니다(5.8M).
• Squeeze-and-Excitation(SE) 모듈을 다양한 압축률(reduction ratio)로 적용했을 때, 압축률이 낮아질수록 정확도가 더욱 증가하는 경향을 보였습니다:
  • SE-192 사용 시 정확도는 74.8%(+2.6%) (5.9M)
  • SE-96 사용 시 정확도는 동일하게 74.8%(+2.6%) (6.0M)
  • SE-48 사용 시 정확도는 75.0%(+2.8%) (6.1M)
  • 압축률을 크게 낮춘 SE-4 사용 시 정확도는 가장 높은 **75.8%(+3.6%)를 기록했으나, 파라미터 수도 9.4M으로 상당히 증가하였습니다.

결론적으로, 비선형 활성화로 h-swish(HS)를 사용하고 SE 모듈을 적절한 압축률로 적용하면, 모델의 정확도를 상당히 높일 수 있으며, 압축률을 크게 낮추면 정확도는 높아지지만 파라미터 수도 크게 증가하는 trade-off를 보입니다.

 

1-3) Placement of Locality and Expansion Ratio

 

 

본 실험은 Transformer 내에서 지역성(locality)을 추가하는 위치가 성능에 미치는 영향을 조사한 것으로, Depth-wise convolution을 Transformer의 어떤 레이어 위치에 적용할 때 성능이 가장 좋은지를 분석한 것입니다.

• 높은 레이어 (9~12)에 locality를 적용하면 성능이 가장 낮아져 정확도가 69.1%로 떨어졌습니다.
• 중간 레이어 (5~8)에 locality를 적용할 때 정확도는 72.1%로 다소 향상됩니다.
• 낮은 레이어 (1~4)에 적용했을 때 정확도는 73.1%로 더욱 좋아졌습니다.
• 레이어의 범위를 더 넓혀 낮은 레이어에 적용하면 정확도는 더 높아져서 74.0%를 기록합니다.
• 모든 Transformer 레이어(1~12)에 depth-wise convolution을 적용하면 파라미터 수가 조금 더 늘어나며(5.91M) 연산량(FLOPs)도 다소 증가하지만, 성능이 가장 높은 74.8%로 나타났습니다.

결론적으로, 지역성을 Transformer의 모든 레이어에 적용하는 것이 최상의 성능을 보이지만, 파라미터와 연산량 증가를 고려할 때, 낮은 레이어 또는 낮은~중간 레이어에만 적용하는 것이 효율적이면서도 뛰어난 성능을 얻을 수 있는 전략임을 시사합니다.

 

 

Feed-forward 네트워크의 확장 비율을 높이면 성능은 명확히 향상되며, 여기에 SE 모듈을 추가로 적용할 경우 성능이 더욱 개선됩니다. 다만 파라미터 수와 연산량이 함께 증가하는 trade-off를 고려할 필요가 있습니다.

 

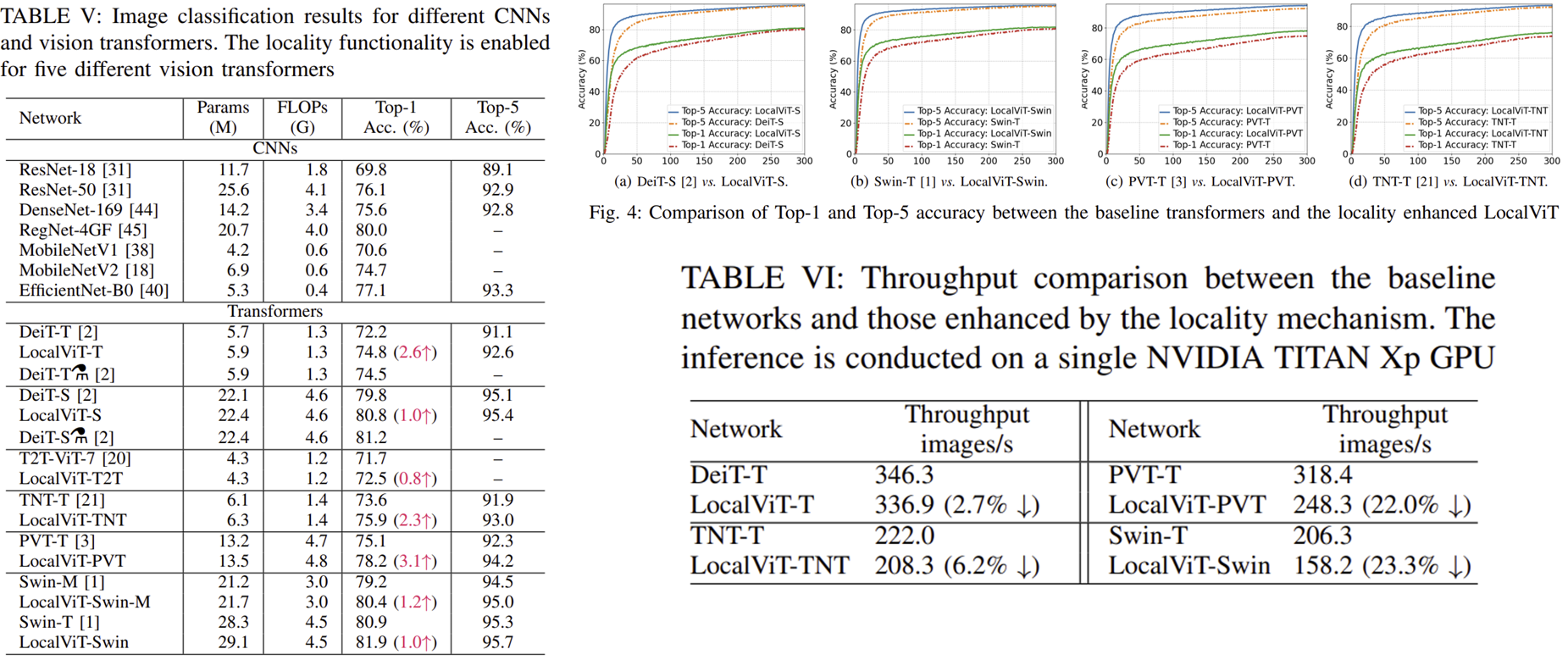
2) Generalization and comparison with state-of-the-art

 

3) Feature Visualization