안녕하세요. 오늘은 CNN과 Transformer의 parallel한 방식으로 혼합하고자했던 TransFuse에 대한 소개를 하도록 하겠습니다.
Background
의료 영상 분할을 대장내시경, 현미경, 초음파, CT, MRI 등 다양한 모달리티 영상에서 폴립, 세포, 유방암, 폐 감염 등 관심 영역을 분할하는 것을 목표로 하고 있습니다. 이를 통해, 진단 보조 시스템과 함께 향후 치료 계획을 수립할 수 있으며 로봇 수술 시에도 중요한 역할을 하고 향후 종양의 성장세를 파악하여 얼마나 약화시킬 수 있는지도 예측할 수 있습니다.
이러한 중요성으로 이전부터 딥 러닝을 이용한 의료 영상 분할을 꾸준히 연구되어 왔습니다. 가장 대표적인 모델이 이전에 제가 소개했던 UNet, UNet++, AttentionUNet일 것 입니다. 이 모델들의 가장 중요한 특징 중 하나는 모든 계층이 합성곱 계층으로 구성되어 있다는 점 입니다. 최신 연구에 따르면 합성곱 계층은 주로 입력 영상 내의 텍스쳐 및 엣지 정보를 기반으로 최종판단을 진행하는 것으로 알려져있습니다. 하지만, 영상의 전체적인 정보 (global context information)을 고려하지 않기 때문에 최적이 아닌 성능을 가지게 되죠. 이러한 문제점을 해결하기 위해 최근 Transformer의 self-attention 매커니즘을 활용하는 모델들도 많이 제시되었습니다. 가장 대표적인 모델이 SwinUNet으로 모든 계층을 오직 Swin Transformer로만 구성한 모델입니다. 이를 통해, 모든 계층에서 성공적으로 입력 영상의 전체적인 정보를 활용할 수 있었지만 CNN이 가지고 있는 중요한 역할인 지역적 특징을 추출하지 못하는 문제점이 있습니다.
이러한 문제점이 입각하여 TransUNet은 CNN에서 추출한 정보를 ViT에게 넘겨 지역적 특징과 전역적 특징을 동시에 고려하였습니다. 하지만, 이는 cascade한 구조로 입력 영상 자체의 전역적 특징을 추출하지 못한다는 문제점이 있습니다. 이러한 문제를 해결하기 위해 오늘 소개하는 TransFuse는 서로 다른 두 모델인 CNN과 Transformer를 병렬로 연결하고 이를 BiFusion이라고 하는 방법으로 이질적인 두 모델의 특징을 결합하는 방식을 제공합니다. 본 논문은 2D과 3D 데이터셋에서 모두 높은 성능을 달성하였습니다.
Proposed Method: TransFuse
1) Overall Architecture
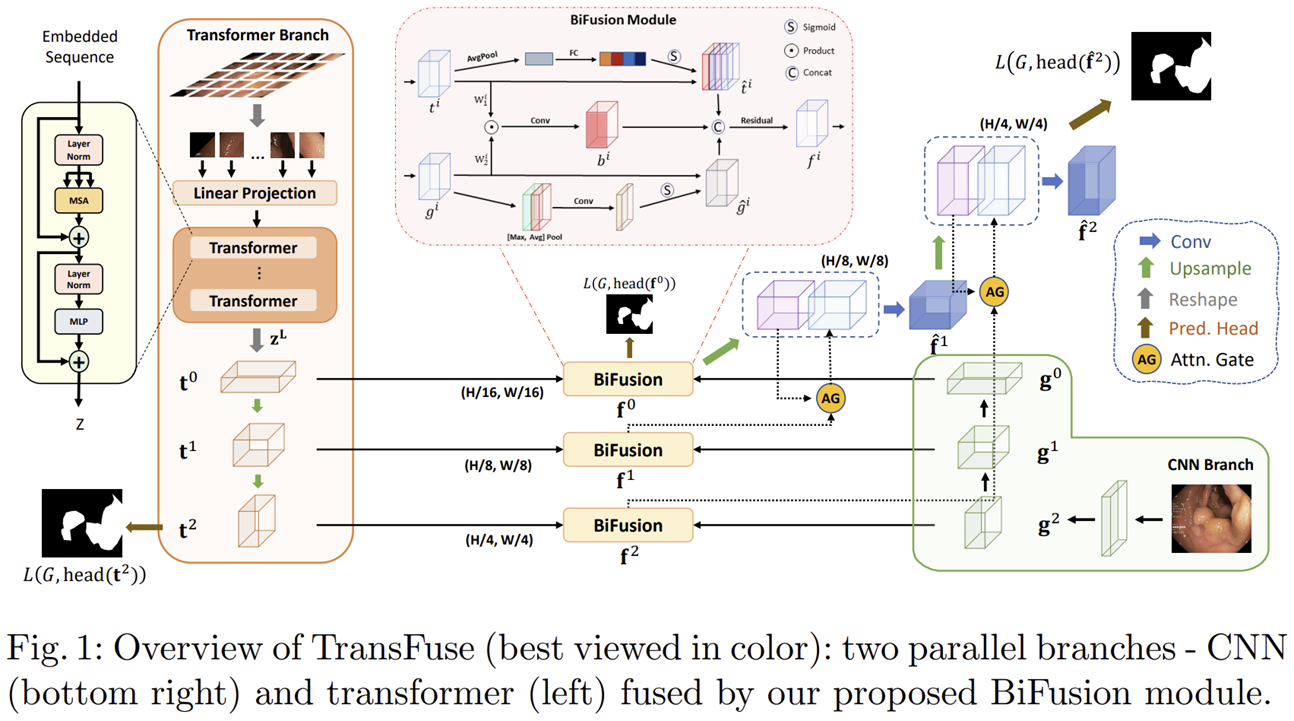
그림 1은 TransFuse의 전체적인 구조를 보여주고 있습니다. 총 4개의 구조로 Transformer Branch, CNN Branch, BiFusion Module 그리고 Attentional Gate Decoder입니다. 사실 본 논문에서 사용되는 매커니즘들은 전부 이전 연구들의 모델 구조를 차용하여 설계하였기 때문에 굉장히 쉽게 이해할 수 있으실거라고 생각됩니다.
2) Transformer Branch
본 논문에서는 기존의 Transformer 구조를 그대로 차용하여 사용하였습니다. 따라서, 입력 영상 $\mathbf{x} \in \mathbb{R}^{H \times W \times 3}$을 $N = \frac{H}{S} \times \frac{W}{S}$개의 균일한 패치로 분할하는 것부터 시작하죠. 여기서 $S = 16$을 사용하였으므로 각 패치의 크기는 $16 \times 16$입니다. 다음으로 각 패치들을 flatten하고 linear projection을 통해 $D_{0}$차원으로 임베딩하여 $\mathbf{e} \in \mathbb{R}^{N \times D_{0}}$로 만들어줍니다. 그리고 지역적 사전정보를 보존하기 위해 positional embedding을 $\mathbf{e}$에 더해주죠. 다음은 저희가 잘 알고 있는 self-attention을 통해 각 토큰들 간의 전역적인 정보를 이해합니다. 이 과정은 총 $L$개의 Transformer 계층으로 구성되고 마지막 계층에서는 Layer Normalization을 적용하여 최종 출력 $\mathbf{z}^{L}$을 얻을 수 있습니다.

이제 Transformer의 최종 출력 $\mathbf{z}^{L}$ 으로부터 예측 마스크를 얻기 위해 Progressive Upsampling (PUP) 구조를 사용하게 되는 데 이는 SETR이라고 하는 Transformer 기반 의미론적 분할 모델에서 차용하였습니다. 위 그림이 SETR에서 사용되는 PUP 구조입니다. 단순히 연속적인 합성곱 디코더로 구성되어있죠. 이를 위해서 먼저 $\mathbf{z}^{L}$의 형상을 2D 특징 맵으로 바꾸어 $\mathbf{t}^{0} \in \mathbb{R}^{\frac{H}{16} \times \frac{W}{16} \times D_{0}}$로 바꾸어줍니다. 다음으로 2개의 연속적인 CNN 디코더를 통과시키며 spatial resolution을 점차 회복시켜 $\mathbf{t}^{1} \in \mathbb{R}^{\frac{H}{8} \times \frac{W}{8} \times D_{1}}$과 $\mathbf{t}^{2} \in \mathbb{R}^{\frac{H}{4} \times \frac{W}{4} \times D_{2}}$을 얻어줍니다. 그리고 $\mathbf{t}^{0}, \mathbf{t}^{1}, \mathbf{t}^{2}$는 모두 저장되어 이후 CNN branch의 특징 맵들과 융합됩니다. 여기서 마지막 특징 맵인 $\mathbf{t}^{2}$에는 $1 \times 1$ 합성곱을 적용하여 Transformer Branch에서의 예측 결과를 얻게 됩니다.
3) CNN Branch
본 논문에서는 기존의 ResNet 블록을 이용하여 설계하기 때문에 이 역시 깊은 설명은 굳이 필요없을 거 같습니다. 다만, Transformer는 일반적으로 4개의 스테이지고 ResNet은 5개의 스테이지이기 때문에 본 논문에서는 ResNet의 마지막 스테이지를 제거하고 사용합니다. 초기 Stem 계층에서 얻는 초기 특징 맵을 제외하고 총 3개의 특징 맵들 $\mathbf{g}^{0} \in \mathbb{R}^{\frac{H}{16} \times \frac{W}{16} \times C_{0}}, \mathbf{g}^{1} \in \mathbb{R}^{\frac{H}{8} \times \frac{W}{8} \times C_{1}} , \mathbf{g}^{2} \in \mathbb{R}^{\frac{H}{4} \times \frac{W}{4} \times C_{2}} $을 얻을 수 있습니다.
4) BiFusion Module

마지막 단계는 Transformer branch와 CNN branch의 결과를 하나로 융합하는 BiFusion Module이 적용됩니다. 이 과정도 사실 아주 쉽게 동작합니다. Transformer branch의 특징 맵에서는 채널 간의 상관성을 이해하기 위해 SE Block을 적용하고 CNN branch에서는 특징 맵에서 공간 정보를 이해하기 위해 CBAM을 적용합니다. 그리고 두 특징 간의 상관성을 고려하기 위해 하나로 fusion한 $\mathbf{b}^{i}$와 함께 세 개의 특징 맵들을 융합한 뒤 마지막으로 residual block을 거쳐 다음 스테이지에 전달이 됩니다.
Experiment Results
1) Comparison with State-of-the-Art Methods
1-1) Quantative Results
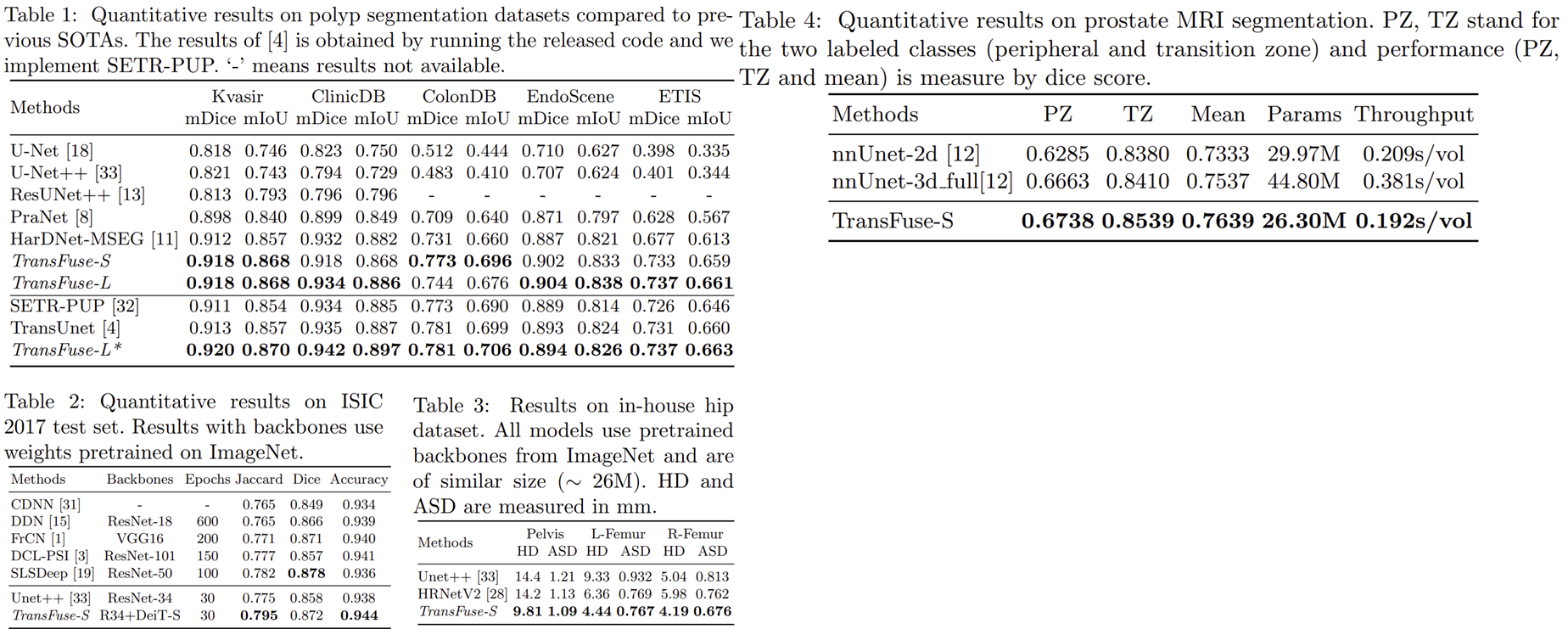
1-2) Qualitative Results

2) Ablation Study
2-1) Parallel-in-Branch Design

2-2) BiFusion Module

'Paper Review' 카테고리의 다른 글
| Fast Fourier Convolution (NIPS2020) (0) | 2025.04.24 |
|---|---|
| EEG Conformer: Convolutional Transformer for EEG Decoding and Visualization (IEEE TNSRE2023) (0) | 2025.04.22 |
| LocalViT: Analyzing Locality in Vision Transformers (arxiv2021) (0) | 2025.04.14 |
| ThiNet: Pruning CNN Filters for a Tinner Net (IEEE TPAMI2018) (0) | 2025.04.08 |
| Deformable Convolutional Networks (ICCV2017) (0) | 2025.04.05 |
