안녕하세요. 오늘은 NIPS2020에 게재되었던 기존의 합성곱 연산을 바꿔 주파수 도메인 관점에서 해석한 Fast Fourier Convolution (FFC)에 대해 소개하도록 하겠습니다.
Background
최근 컴퓨터 비전 기술은 객체 인식, 이미지 분할, 객체 탐지 등 다양한 분야에서 뛰어난 성과를 보여주고 있습니다. 특히, 이미지 내에 있는 객체의 위치나 형태를 정확히 인식하고 구분하는 기술은 자율주행, 보안 감시, 의료 영상 분석 등 많은 실생활 응용 분야에서 필수적입니다. 특히, 최근에 많이 활용되는 합성곱 신경망 (Convolutional Neural Network; CNN)은 이미지의 지역적 (local) 특징을 잘 포착하는 데 강점을 가지고 있습니다. 이러한 지역적 특징을 가진 합성곱 계층을 여러 개 쌓고 점진적인 다운샘플링을 적용함으로써 최종적으로는 특징 맵의 전역적인 정보를 이해할 수 있다고 알려져 있죠. 하지만 이와 같은 비명시적 전역적인 정보로는 충분한 성능을 낼 수 없다고 본 논문에서는 주장하고 있습니다. 이때, 본 논문에서 특히 관심을 가진 부분은 Fourier Transform입니다.
$$f(x, y) * g(x, y) \Leftrightarrow F(u, v) \cdot G(u, v)$$
위 수식은 Convolution Theorem입니다. 간단하게 설명하면 spatial domain인 합성곱 ($f(x, y) * g(x, y)$)은 spectral domain의 곱 ($F(u, v) \cdot G(u, v)$)와 동일하다는 정리입니다. 이 과정에서 spectral domain에 어떤 값을 딱 하나만 변화를 준다고 가정하면 이는 spatial domain의 모든 값에 영향을 주기 때문에 non-local receptive field를 활용할 수 있을 것으로 볼 수 있습니다. 본 논문에서는 Fourier Transform의 이러한 특징을 이용해서 모델을 설계하여 Fast Fourier Convolution (FFC)라는 새로운 합성곱 연산 기법을 제안하였습니다.
Proposed Method: Fast Fourier Convolution
1) Architecture Design

그림 1은 FFC의 전체적인 구조를 보여주고 있습니다. 크게 두 가지 경로 (local branch와 global branch)로 구성되어 있습니다. 그리고 local branch의 경우 사용되는 변환 $f_{l}(\cdot)$은 기존의 합성곱 연산을 동일하게 사용하여 지역적인 특징을 추출합니다. 그리고 local branch에서 global branch로 옮겨질때 사용되는 변환 $f_{l \rightarrow g}(\cdot)$과 그 반대의 변환 $f_{g \rightarrow l}(\cdot)$은 역시도 기존의 합성곱 연산을 동일하게 사용합니다. 따라서 본 논문의 핵심은 global path 내에서 사용되는 $f_{g} (\cdot)$입니다. 이 변환은 오직 spectral domain에서만 수행됩니다.
일단 일차적으로 입력 특징맵 $\mathbf{X} \in \mathbb{R}^{H \times W \times C}$를 채널 중심으로 두 개의 특징맵 $\mathbf{X} = \{ \mathbf{X}^{l}, \mathbf{X}^{h} \}$로 분해합니다. 여기서 $\mathbf{X}^{l} \in \mathbb{R}^{H \times W \times (1 - \alpha_{\text{in}})C}$는 지역적인 특징을 얻을 것을 기대하고 $\mathbf{X}^{g} \in \mathbb{R}^{H \times W \times \alpha_{\text{in}}C}$는 전역적인 특징을 이해할 것이라고 기대합니다. 이때, $\alpha_{\text{in}} \in [0, 1]$은 global branch에 할당되는 채널의 비율을 의미합니다.
다음으로 $\mathbf{X} = \{ \mathbf{X}^{l}, \mathbf{X}^{h} \}$에 대해서 본 논문에서 제안하는 FFC를 다음과 같이 적용합니다.
$$\begin{cases} &\mathbf{Y}^{l} = \mathbf{Y}^{l \rightarrow l} + \mathbf{Y}^{g \rightarrow l} = f_{l}(\mathbf{X}^{l}) + f_{g \rightarrow l} (\mathbf{X}^{g}) \\ &\mathbf{Y}^{g} = \mathbf{Y}^{g \rightarrow g} + \mathbf{Y}^{l \rightarrow g} = f_{g}(\mathbf{X}^{g}) + f_{l \rightarrow g} (\mathbf{X}^{l}) \end{cases}$$
2) Implementation Detalils
본 논문의 목표는 최대한 효율적인 방식으로 receptive field를 최대한 늘리는 것 입니다. 이를 위해 본 논문에서는 convolution theorem을 기반으로 동작하는 FFC를 제안하기로 하였죠. 여기서 핵심은 local branch와 global branch로 분해할 때 global branch 내의 연산인 $f_{g}(\cdot)$이라고 볼 수 있습니다.
일단 ResNet에서 bottleneck 구조에서 영감을 받아 본 논문에서도 연산 앞뒤에 $1 \times 1$ 합성곱 계층을 도입하여 효율적인 연산을 수행할 수 있도록 하겠습니다. 다음에 진행되는 연산이 $f_{g}(\cdot)$, 즉 spectral Transformer라고 불리는 새로운 합성곱 연산으로 Fourier Unit (FU) 와 Local Fourier Unit (LFU)로 구성되어 있습니다. 여기서 Fourier Unit은 전역적인 receptive field로 동작하며 Local Fourier Unit은 준-전역적인 receptive field로 전역적인 특징과 지역적인 특징의 중간의 연산으로 구성됩니다.
LFU는 사실 FU를 기반으로 동작하기 때문에 FU만 이해하면 아주 쉽게 이해할 수 있습니다. 기본적으로 주어진 특징 맵을 spectral domain으로 바꾸어줍니다. 이 과정에서 본 논문에서는 Cooley-Tukey Algorithm 기반의 DFT를 사용하는 데 이는 DFT의 연산 속도를 향상시키는 핵심 알고리즘입니다. 하지만 여기서는 범위를 벗어나기 때문에 이후에 시간이 된다면 설명을 하도록 하겠습니다. 다음 단계에서는 spectral data를 update를 수행한 뒤 inverse DFT를 이용해서 다시 spatial domain으로 되돌려주면 됩니다. 여기서 궁금증이 있습니다. 일반적으로 DFT를 적용하면 실수부와 허수부가 나와서 어떻게 이 복소수를 처리하는 지가 pytorch의 연산과 연동할 수 있는 지에 대한 큰 관건일 것 입니다.

이를 위해 본 논문에서는 위의 의사코드와 같이 실수부와 허수부를 채널 레벨로 하나로 concat하고 일반적인 합성곱을 진행합니다. 그리고 두 개를 다시 분해한 뒤 inverse DFT를 적용하여 다시 spatial domain으로 되돌리죠. 여기서 이상한 점은 연산을 오직 $\lfloor \frac{W}{2} \rfloor$에서만 진행하는 것을 볼 수 있죠? 이는 DFT의 특성상 임의의 실수값을 가지는 신호에 DFT를 취하면 항상 Hermitian Matrix이 나오기 때문에 원점을 중심으로 대각선 방향은 대칭상태이기 때문입니다. 따라서 아래는 굳이 연산을 하지 않는 것을 볼 수 있죠. 또한, spectral domain에서의 값을 하나만 변경해도 그에 대응되는 spatial domain은 모든 영향을 받기 때문에 본 논문에서는 $1 \times 1$ 합성곱을 적용합니다. 그럼에도 불구하고 spatial domain에서는 전역적인 receptive field로 수행되는 것과 마찬가지인거죠.

마지막 단계는 LFU입니다. 사실 이는 입력 특징 맵을 4개로 다시 분할하고 이를 채널 단위로 다시 합친뒤 FU를 거치는 것과 동일하기 때문에 더 자세한 설명은 하지 않아도 될 거 같습니다.
3) Computational Complexity

Experiment Results
1) Ablation Study
1-1) Different Ratios on ImageNet

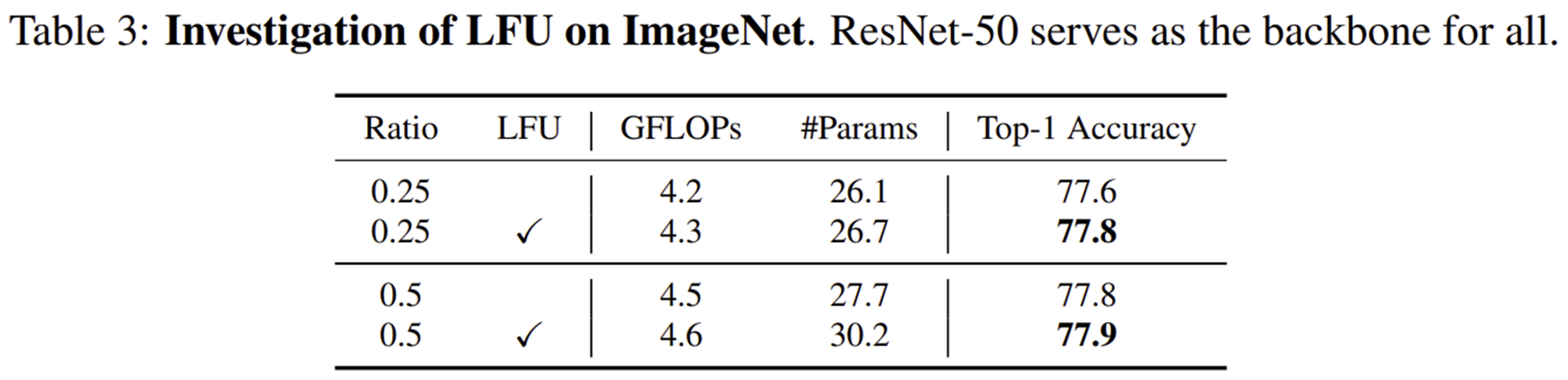
1-2) Investigation of LFU on ImageNet
2) Image Classification

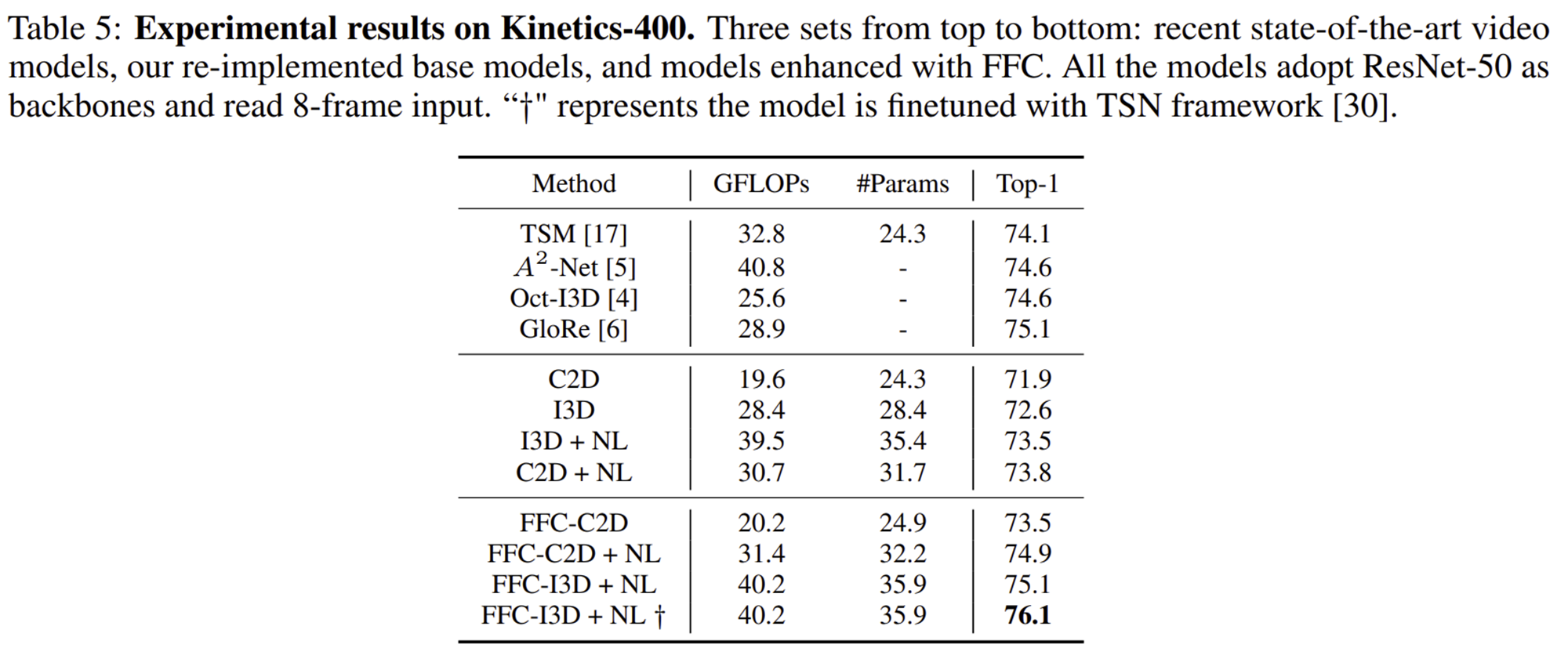
3) Video Recognition
4) Human Key Point Detection

