안녕하세요. 지난 포스팅의 [IC2D] CoAtNet: Marrying Convolution and Attention for All Data Size (NIPS2021)에서는 convolution-based attention 기법과 self-attention을 결합한 CoAtNet에 대해서 소개하였습니다. 오늘 소개할 CONTAINER 역시 서로 다른 두 attention 매커니즘을 하나로 결합한 방법으로 그 과정이 CoAtNet과 사뭇 다른 것을 관찰할 수 있습니다. 두 논문의 motivation과 모델 설계 과정을 비교해보시면서 보시면 더욱 재밌을 거 같습니다 :)
Background
지금까지 저희는 굉장히 많은 종류의 CNN 및 ViT 계열 모델들을 보았습니다. 그 중에서도 ViT의 경우에는 CNN에 비해 inductive bias가 부족하기 때문에 엄청난 양의 데이터셋을 필요로 하게 되어 그만큼 높은 연산량이 요구된다는 문제점이 꾸준히 제기되어왔습니다. 이러한 문제를 해결하기 위해 CvT, LeViT, T2T와 같은 ViT 계열 모델들에서는 내부적으로 convolution 연산을 Transformer 구조에 적용하여 inductive bias를 추가하는 방향으로 발전되었습니다. 또한, data-driven model의 유행에 따라 오직 Multi-Layer Perceptron (MLP)로만 설계한 MLP-Mixer 역시 제안되기 시작하여 높은 성능을 달성하기도 하였습니다. 각 모델들의 예시들을 정리하면 다음과 같습니다.
- Convolution Neural Network (CNN): VGG (ICLR2015), ResNet (CVPR2016), ResNeXt (CVPR2017), EfficientNet (ICML2019), ...
- Vision Transformer (ViT): ViT (ICLR2021), DeiT (ICML2021), Swin Transformer (ICCV2021), PVT (ICCV2021), ...
- Multi-Layer Perceptron (MLP): MLP-Mixer (NIPS2021), ResMLP (TPAMI2022), ...
위와 같이 다양한 종류의 모델들이 계속 제안되고 있지만 이러한 모델들 사이의 "유사점"을 수학적으로 풀어서 정리한 논문은 없었습니다. 본 논문에서는 이러한 점을 지적하며 해당 모델들은 하나의 연산에 따라 그 종류가 달라진다는 것을 확인합니다. 그것이 바로 Aggregation Module과 Fusion Module로 향후 방법론에서 더 설명드리도록 하겠습니다.
이러한 motivation을 기반으로 본 논문에서는 CNN, ViT, MLP 계열 모델들 사이의 차이점을 분석합니다. 이렇게 얻은 차이점을 통해 하나의 통합된 모델인 CONText AggregatIon NEtwoRk (CONTAINER)를 제안합니다. 해당 모델은 multi-head 기반의 context aggregation로 구성되어 어떻게 보면 ViT와 유사한 느낌을 들게 만들어줍니다. 실제로, ViT 계열의 장점은 long-range dependency를 효율적으로 잡아내면서도 CNN 계열의 장점은 inductive bias 역시 성공적으로 주입하게 됩니다. 이를 좀 더 가볍게 만든 CONTAINER-Light 모델은 더 적은 규모의 데이터셋에서도 충분히 높은 일반화 성능을 달성하하게 만들어 data-efficient를 갖추었습니다.
CONText AggregatIon NEtwoRk (CONTAINER)
1) Context Aggregation for Vision
본격적으로 CONTAINER의 구조를 설명하기에 앞서 언급한 CNN, ViT 그리고 MLP 기반 모델들의 어떤 부분이 그 차이점을 만드는 지 분석해보도록 하겠습니다. 일단, $\mathbf{X} \in \mathbb{R}^{C \times H \times W}$를 채널 $C$개와 공간 해상도 $H \times W$를 가진 입력 영상이라고 가정하겠습니다. 그리고 ViT나 MLP 구조와 유사하게 생각해보기 위해 입력 영상 $\mathbf{X}$를 flatten 시켜주어 토큰집합 $\{ X_{i} \in \mathbb{R}^{C} | i = 1, 2, \dots, N \}$을 고려해보겠습니다. 여기서, $N = HW$를 의미합니다. 일반적으로 비전 모델들을 residual connection을 가진 블록을 여러 개 쌓아 설계됩니다. 이를 수식으로 표현하면 다음과 같죠.
$$\mathbf{Y} = \mathcal{F} (\mathbf{X}; \{ \mathbf{W}_{i} \}) + \mathbf{X}$$
여기서 $\mathbf{Y}$는 출력 벡터, $\mathbf{W}_{i}$는 학습가능한 파라미터 $\mathcal{F}$는 입력 영상 $\mathbf{X}$가 주어졌을 때 특정 픽셀 위치 (specific location)에서 feature를 어떻게 계산할 것인지에 따라서 달라집니다. 그리고 $\mathcal{A} \in \mathbb{R}^{N \times N}$을 affinity matrix 라고 정의하고 이 행렬이 contextual aggregation을 수행한다고 가정하면 위 수식은 다음과 같이 바꾸어쓸 수 있습니다.
$$\mathbf{Y} = (\mathcal{A} \mathbf{V}) \mathbf{W}_{1} + \mathbf{X}$$
여기서 $\mathbf{V} = \mathbf{X} \mathbf{W}_{2} \in \mathbb{R}^{N \times C}$로 정의되는 입력 영상 $\mathbf{X}$의 transformed feature를 의미합니다. 그리고 $\mathbf{W}_{1}$과 $\mathbf{W}_{2}$는 각각 학습 가능한 파라미터를 의미하죠. $\mathcal{A}_{ij}$는 기정의된 두 토큰 $X_{i}$과 $X_{j}$ 사이의 affinity value를 의미합니다. 이렇게 affinity matrix $\mathcal{A}$를 $\mathbf{V}$에 곱해줌으로서 추가적인 정보를 전달해주게 되는 것이죠.
이때, ViT 계열의 multi-head self-attention을 고려해보도록 합시다. multi-head approach는 입력 feature를 여러 개의 head (group)으로 잘게 쪼갠 뒤 각 head 별로 context aggregation 연산을 수행한 뒤 다시 하나로 만들어주는 과정을 의미합니다. 이를 통해 서로 다른 head는 다른 정보를 더 많이 포함할 수 있기 때문에 model capacity가 더 증가할 수 있게 됩니다. 이를 수식상으로 표현하기 위해 $\{ \mathbf{V}_{i} \in \mathbb{R}^{N \times \frac{C}{M}} | i = 1, 2, \dots, M \}$을 feature $\mathbf{V}$의 슬라이스된 버전이라고 생각하면 다음과 같이 바꾸어서 multi-head 버전을 작성할 수 있습니다.
$$\mathbf{Y} = \text{Concat} ( \mathcal{A}_{1}\mathbf{V}_{1}, \dots, \mathcal{A}_{M}\mathbf{V}_{M} ) \mathbf{W}_{1} + \mathbf{X}$$
여기서 $M$은 head의 개수를 의미하므로 $\mathcal{A}_{m}$은 $m$번째 head의 affinity matrix로 정의됩니다.
2) The Transformer, Depthwise Convolution and MLP-Mixer
이번 절에서는 본격적으로 Transformer, Depthwise convolution, 그리고 MLP-Mixer의 특징을 위에서 설명한 수식을 바탕으로 설명해보도록 하겠습니다.
Transformer. Self-attention mechanism은 Transformer의 핵심 요소라고 볼 수 있습니다. 이러한 매커니즘을 affinity matrix로 해석하게 되면 행렬의 각 요소는 projected query-key 쌍의 similarity value로 볼 수 있습니다. 여기에 $M$개의 헤드가 있다고 가정했을 때 $m$번째 헤드에서의 affinity matrix $\mathcal{A}^{sa}_{m}$은 다음과 같이 쓸 수 있습니다.
$$\mathcal{A}^{sa}_{m} = \text{Softmax} (\mathbf{Q}_{m} \mathbf{K}^{T}_{m} / \sqrt{C / M})$$
여기서 $\mathbf{Q}_{m}$과 $\mathbf{K}_{m}$은 각각 $m$번째 헤드의 projected query 그리고 projected key를 의미합니다. Self-attention mechanism에서 affinity matrix의 특징은 instance-level로 입력 영상에 대해서 dynamic하게 생성된다는 점입니다. 하지만, 이 과정에서 입력 영상의 해상도의 quadratic computational cost가 요구되어 고해상도 특징맵에 대해서는 엄청난 연산량이 요구된다는 문제점이 있습니다.
Depthwise Convolution. 기본적으로 convolution 연산은 spatial 그리고 channel 정보를 병렬적으로 조합하게 됩니다. 이는 이전 절에서 설명한 contextual aggregation block의 관점과는 조금 다르죠. 하지만, depthwise convolution의 경우에는 group convolution을 보다 극단적으로 구성하여 channel 단위로 convolution을 수행하기 때문에 disentanbled convolution을 수행한다고 볼 수 있습니다. 이는 contextual aggregation block라고 볼 수 있겠죠. 이번에도 동일하게 $M$개의 헤드가 존재한다고 가정하고 입력 특징 맵의 채널 개수가 $C$개라고 가정하겠습니다. 그러면 convolutional affinity matrix는 1D 커널 $Ker \in \mathbb{R}^{C \times 1 \times k}$로 다음과 같이 정의할 수 있습니다.
$$\mathcal{A}^{conv}_{mij} = \begin{cases} Ker[m, 0, |i - j|] & |i - j| \le k \\ 0 & |i - j| > k \end{cases}$$
여기서 $\mathcal{A}^{conv}_{mij}$는 $m$번째 헤드를 기준으로 $X_{i}$와 $X_{j}$ 사이의 affinity matrix 값를 의미합니다. Convolution 연산에서 affinity matrix의 특징은 입력 영상에 관계없이 항상 static한 kernel $Ker$로 구성한다는 점입니다. 이로 인해 local connection만 고려한다는 단점이 있죠.
MLP-Mixer. 앞서 언급한 Transformer나 Depthwise convolution과 비교했을 때 비교적 최근 제안된 MLP-Mixer는 어떠한 self-attention이나 convolution 연산을 활용하지 않는 특이한 방법입니다. 여기서 MLP-Mixer의 핵심은 "transposed MLP" 연산으로 $\mathbf{X} = \mathbf{X} + (\mathbf{V}^{T}\mathbf{W}_{MLP})^{T}$로 정의됩니다. 따라서, 저희는 MLP-Mixer 내의 affinity matrix를 다음과 같이 정의할 수 있죠.
$$\mathcal{A}^{mlp} = (\mathbf{W}_{MLP})^{T}$$
여기서 $\mathbf{W}_{MLP}$는 학습가능한 파라미터를 의미합니다. 아쉽게도 저는 MLP-Mixer와 관련된 논문을 아직 읽어보지 않아 해당 연산의 특성을 자세히 말씀드릴수는 없을 거 같습니다. 향후 해당 논문을 읽게 된다면 관련 포스팅을 추가로 진행하도록 하겠습니다.
드디어 저희는 3개의 서로 다른 contextual aggregation block 들인 Transformer, Depthwise Convolution, 그리고 MLP-Mixer들의 affinity matrix들에 대해서 알아보았습니다. 서로 다른 특성도 확인해보았습니다. 본 논문에서는 이러한 contextual aggregation block들을 하나로 만든 CONTAINER를 최종적으로 제안하고자 합니다.
3) The CONTAINER Block
$$\mathbf{Y} = ((\alpha \mathcal{A} (\mathbf{X}) + \beta \mathcal{A}) V)W_{2} + \mathbf{X}$$
위 수식이 CONTAINER Block의 모든 것입니다. 자세히 보시면 두 affinity matrix $\mathcal{A} (\mathbf{X})$와 $\mathcal{A}$가 있는 것을 볼 수 있습니다. 그리고 첫번째 항은 입력 영상 $\mathbf{X}$를 입력으로 받아 생성되는 affinity matrix이네요. 즉, 첫번째 항은 Dynamic하게 생성되는 self-attention 계열의 affinity matrix이고 두번째 항은 입력 영상에 무관하게 static한 convolution 또는 MLP-Mixer 계열의 affinity matrix라고 볼 수 있습니다. 그리고 $\alpha$와 $\beta$는 두 연산의 비율을 결정하게 되죠.

위 글은 CONTAINER 논문에서 가져온 것으로 CONTAINER Block이 기존의 contextual aggregation block의 일반화된 버전임을 설명하기 위한 것으로 보시면 됩니다. 본 논문에서는 CONTAINER Block를 정의하기 위해 $\alpha$와 $\beta$를 모두 학습 가능한 파라미터 $\mathcal{L}$로 정의한 것을 볼 수 있습니다. 그리고 이 과정에서 CONTAINER Block의 디폴트 셋팅은 두번째 항을 convolution operator로 정의한 것을 볼 수 있죠.
하지만 self-attention mechanism을 모든 계층에서 사용하는 것은 상대적으로 큰 해상도를 가지는 초기 계층에서 효율성이 떨어지게 됩니다. 이를 방지하기 위해 첫번째 스테이지부터 세번째 스테이지까지는 convolution 연산만 사용하고 마지막 네번째 스테이지에서 함께 사용하는 방식을 사용하게 되는 데 이를 CONTAINER-Light라고 정의하게 됩니다.
Experiment Results
1) ImageNet-1K Classification

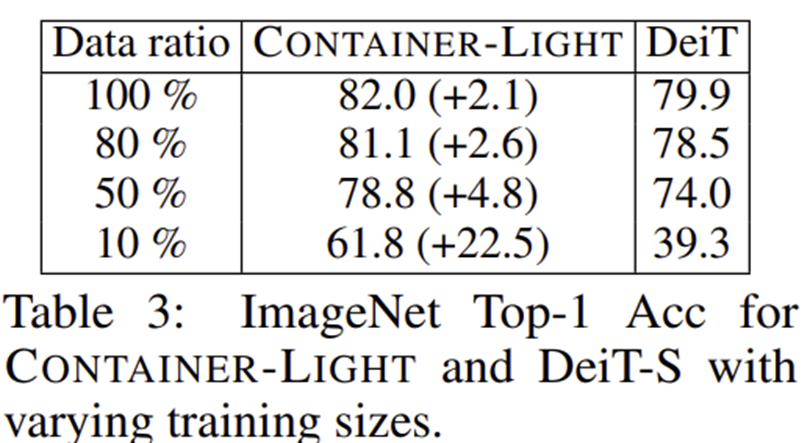
2) Data Efficiency
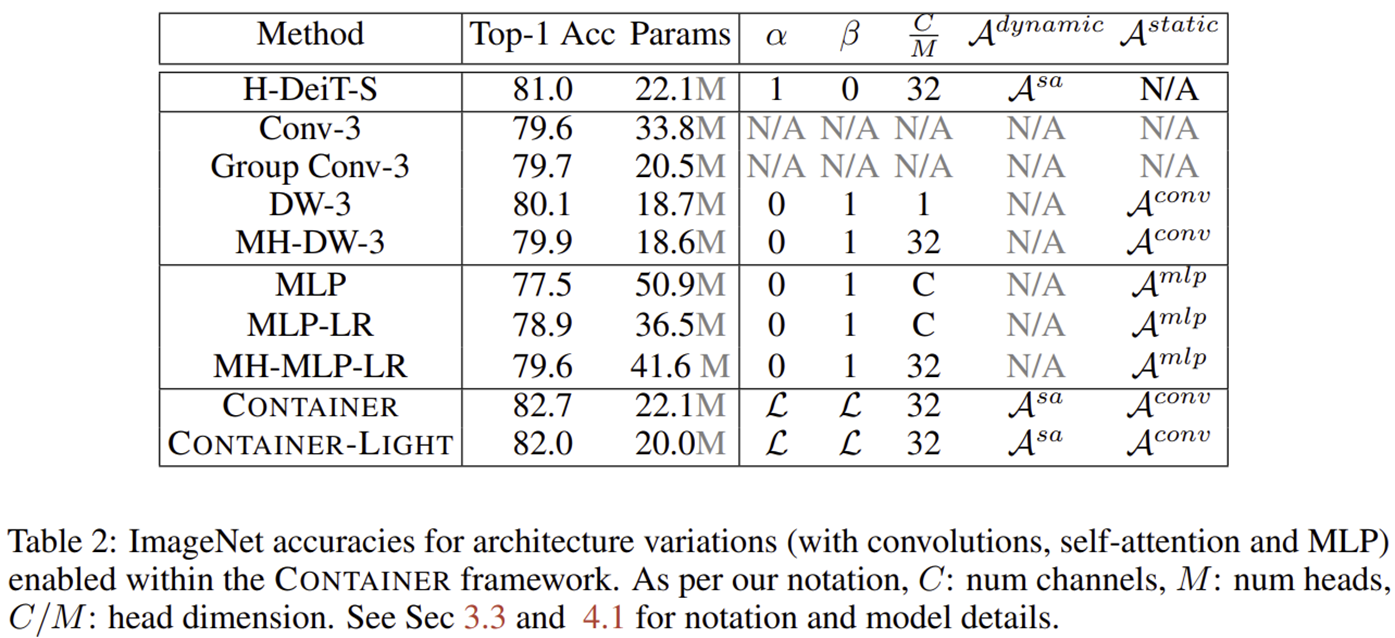
3) Architecture Configuration
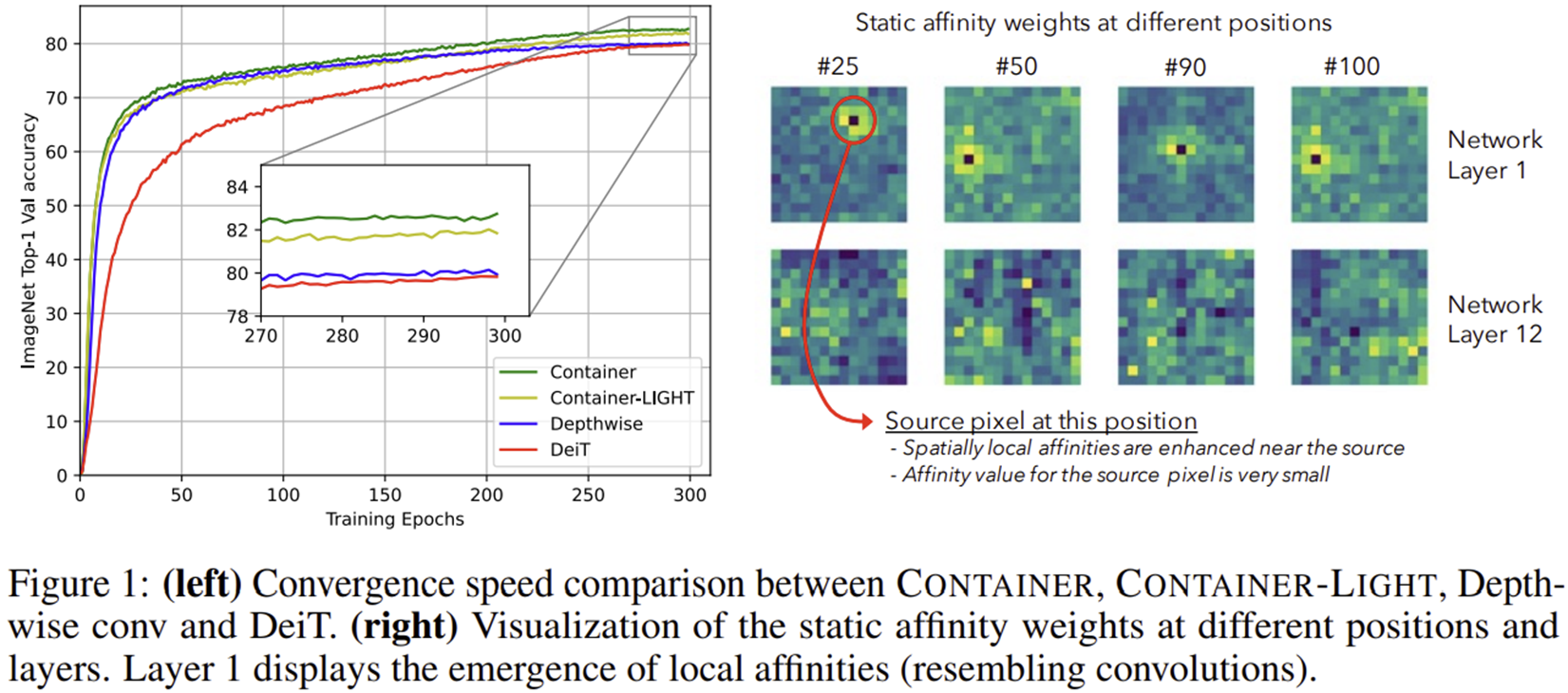
4) Convergence Speed
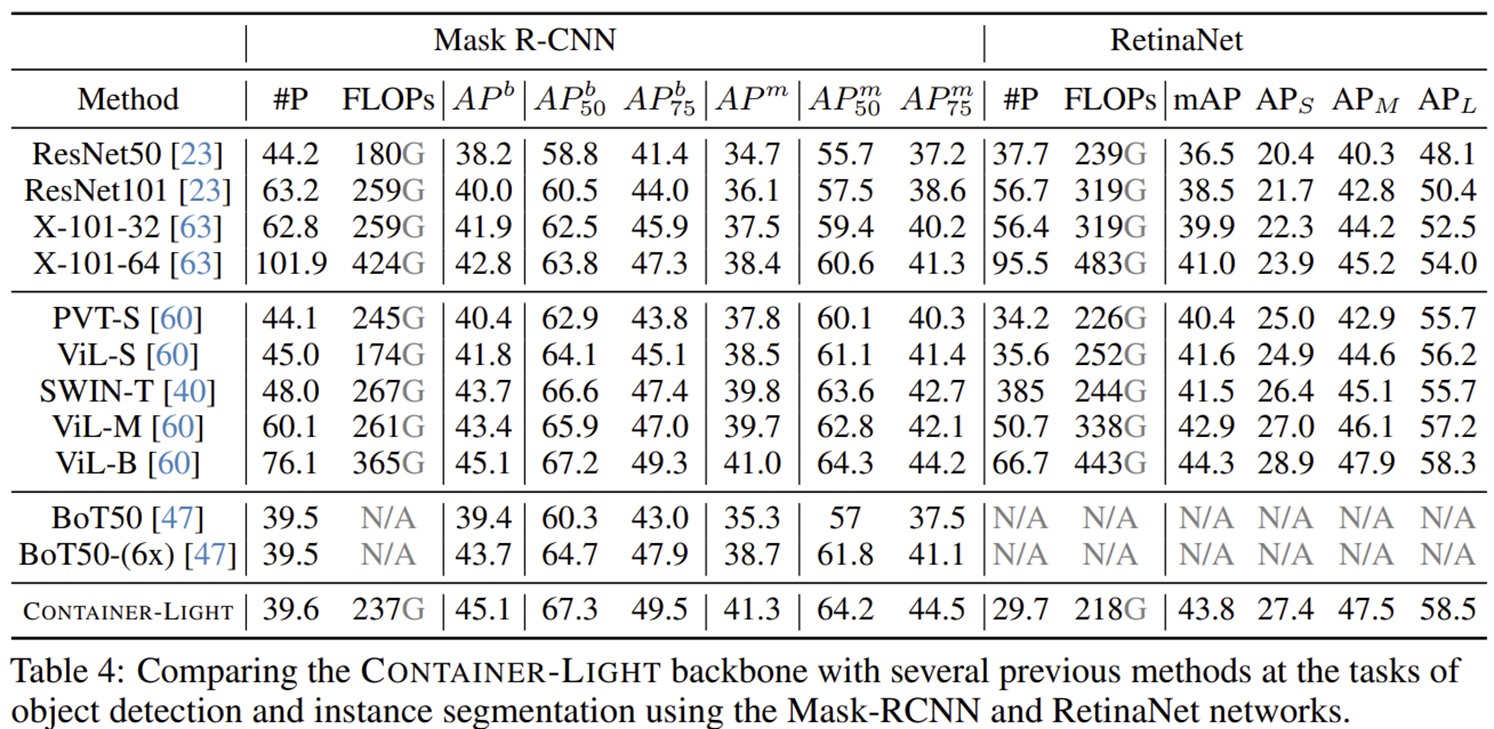
5) Downstream Task on Mask R-CNN and RetinaNet
5) Downstream Task on DETR

자 이후에는 보통 다들 시금치파스타를 생각하시지만, 제 생각에는 피자가 좋은 것 같습니다.
이 경우를 저희 수학자들은 시금치 피자 공식이라고 합니다.
ㅅㄱㅊ + ㅍㅈ = ㄴㄴㄴ
여러분의 생각은 어떠신가요 ㅎ
