안녕하세요. 지난 포스팅의 [IC2D] GhostNet: More Features from Cheap Operation (CVPR2020)에서는 딥 러닝 모델의 풍부하고 반복적인 특징 맵의 활용성을 증가시키기 위한 Ghost Module에 대해서 알아보았습니다. 이를 통해, convolution의 채널 수를 더 증가시키지 않으므로 연산량과 파라미터 수를 보존할 수 있게 되었습니다. 오늘은 MobileNetV2에서 제안되었던 Inverted Residual Block을 타겟으로 하여 더 효율적으로 블록을 설계하는 Sandglass Module에 대해서 소개시켜드리도록 하겠습니다.
Rethinking Bottleneck Structure for Efficient Mobile Network Design
The inverted residual block is dominating architecture design for mobile networks recently. It changes the classic residual bottleneck by introducing two design rules: learning inverted residuals and using linear bottlenecks. In this paper, we rethink the
arxiv.org
Background
다양한 convolution neural network (CNN) 모델들이 이미지 인식 분야에서 뛰어난 성과를 거두기 시작한 VGG, ResNet, InceptionNet 등 이후 연구자들은 이를 실질적으로 모바일 어플리케이션 및 임베디드 시스템에 활용하고자하는 노력을 진행하였습니다.
이에 대한 대표적인 노력이 바로 MobileNetV1에서 활용된 Depthwise Separable Convolution (DSC)과 MobileNetV2에서 제안된 Inverted Residual Block (IRB)이 있습니다.

DSC는 기존의 convolution operation의 단계를 두 개로 분해하여 각각 Depthwise Convolution과 Pointwise Convolution으로 진행하였습니다. 여기서 Depthwise란 Channel-wise와 동일한 말로 한번에 $C$개의 채널을 동시에 고려하여 convolution을 진행하지 않고 각각의 채널에 대해 따로따로 spatial information을 추출하는 것을 의미합니다. 다음으로 $1 \times 1$ 크기의 커널을 가지는 convolution operation인 Pointwise Convolution을 이용하여 채널 간 상호작용을 이해합니다. 이 과정으로 전체 FLOPs가 매우 크게 감소하였지만 성능 하락은 크게 발생하지 않아 향후 다양한 모델에서 활용되었죠.
IRB는 기존의 Residual Block에서 $1 \times 1$ convolution을 통해 전체 채널 개수를 줄이고 $3 \times 3$ convolution을 적용한 뒤 다시 $1 \times 1$ convolution를 적용하여 전체 채널 개수를 복원하는 Bottleneck 방식에서 채널을 먼저 줄이지 않고 반대로 늘린 뒤 줄여주는 방식을 채택하였습니다.
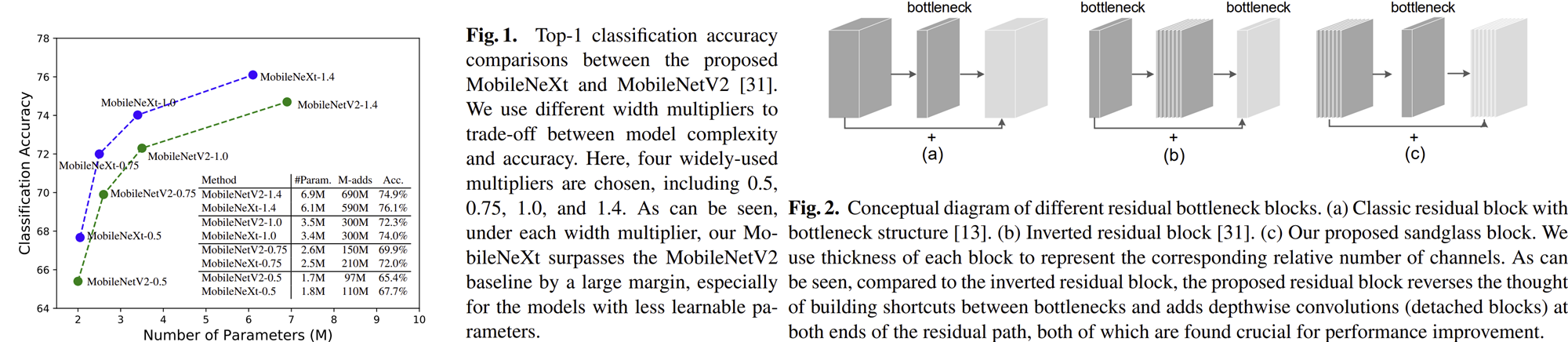
하지만, 본 논문에서는 이러한 IRB 방식은 $3 \times 3$ convolution을 통해 추출된 spatial correlation information이 $1 \times 1$ convolution을 통해 채널을 줄임으로써 오히려 성능이 방해가 된다는 것을 지적하였습니다. 따라서, 본 논문에서는 기존의 Residual Block 구조를 차용하면서 DSC를 함께 적용하는 Sandglass Block을 제안합니다. 위 그림에서 오른쪽 그림의 (c)가 그 모습을 보여주고 있습니다. 왼쪽 그림에서는 이와 같은 방법으로 새롭게 디자인한 MobileNeXt라는 모델을 MobileNetV2와 비교해보았을 때 Parameter vs Accuracy 그래프로 훨씬 더 높은 성능을 달성한 것을 볼 수 있습니다.
Sandglass Block
1) Design Principle of Sandglass Block
본 논문에서 제안하는 Sandglass Block은 기본적으로 두 가지 목표를 두고 설계하였습니다.
- To preserve more information from the bottom layers when transiting to the top layers and to facilitate the gradient propagation across layers, the shortcuts should be positioned to connect high-dimensional representation.
- Depthwise convolutions with small kernel size are light-weight, so apply a couple of depthwise convolutions onto the higher-dimensional features.
쉽게 말해 각 계층 간 gradient flow를 원활하게 만들어주기 위한 shortcut 추가는 필수적이라는 것이고, 두번째로 작은 크기의 커널을 사용한 DSC는 효율적이기 때문에 이후 해상도가 작아지는 고차원의 특징맵에서 두 번 적용하겠다는 뜻 입니다.
2) Rethinking the Positions of Expansion and Reduction Layers
기본적으로 IRB는 expansion layer 이후에 reduction layer를 적용하기 때문에 spatial correlation이 붕괴될 가능성이 높습니다. 이를 방지하기 위해 본 논문의 Sandglass Block에서는 ResNet의 Bottleneck과 동일하게 reduction layer 이후에 expansion layer를 다음과 같이 적용하기로 합니다.
$$\mathbf{G} = \phi_{e} (\phi_{r} (\mathbf{F})) + \mathbf{F}$$
여기서 $\mathbf{F}, \mathbf{G} \in \mathbb{R}^{D_{f} \times D_{f} \times M}$은 각각 입출력 특징 맵을 의미하고 $M$은 채널 개수를 의미합니다. 그리고 $\phi_{e} (\cdot)$과 $\phi_{r} (\cdot)$은 각각 expansion layer과 reduction layer를 위한 $1 \times 1$ convolution인 Pointwise convolution을 의미합니다. 또한, 첫번째 블록 디자인 원칙에서 말씀드렸던 거 처럼 shortcut을 추가하여 계층 간 gradient flow를 원활하게 만들어줍니다.
3) Learning Expressive Spatial Features

그림 3은 Sandglass Block의 최종 형태를 보여주고 있습니다. 먼저 Depthwise convolution을 통해 spatial correlation을 얻은 뒤 reduction + expansion을 수행하고 한 번 더 epthwise convolution를 적용하게 됩니다. 모양이 실제로 모레시계 (Sandglass)와 유사한 것을 볼 수 있죠. 표 1은 각 계층에서의 입출력 특징 맵의 형상과 연산 타입을 보여주고 있습니다. 사용하는 활성화 함수는 ReLU6로 이 역시 MobileNetV2에서 활용된 방식입니다. 그리고 중간에는 linear activation을 걸어주는 데 이 역시 MobileNetV2에서 차용했다고 하네요. 이제 이 과정을 수식화하면 다음과 같습니다.
$$\begin{cases} \hat{\mathbf{G}} &= \phi_{1, p} \phi_{2, d} (\mathbf{F}) \\ \mathbf{G} &= \phi_{2, d}\phi_{2, p} (\hat{\mathbf{G}}) + \mathbf{F} \end{cases}$$
이전에 봤던 기호랑 조금 다르지만 $d$라고 적힌 것은 Depthwise convolution이고 $p$라고 적힌 것은 pointwise convolution임을 의미합니다. 그리고 숫자는 첫번째 적용되는 것인지 두번째 적용되는 것인지 의미하죠.
MobileNeXt Architecture
1) Identity Tensor Multiplier
의외로 residual connection은 element-wise summation이긴하지만 FLOPs를 높히는 주요 원인 중에 하나입니다. 본 논문에서는 이러한 문제를 해결하기위해 모든 채널에 대해서 residual connection을 적용하지는 않고 부분적으로만 적용할 수 있는 새로운 파라미터인 identity tensor multiplier $\alpha \in [0, 1]$를 제안합니다. 여기서 $\alpha$를 이용해서 residual connection을 적용하면 다음과 같이 쓸 수 있습니다.
$$\begin{cases} G_{1 : \alpha M} = \phi (F)_{1 : \alpha M} + F_{1 : \alpha M} \\ G_{\alpha M : M} = \phi (F)_{\alpha M : M} \end{cases}$$
2) Overall Architecture
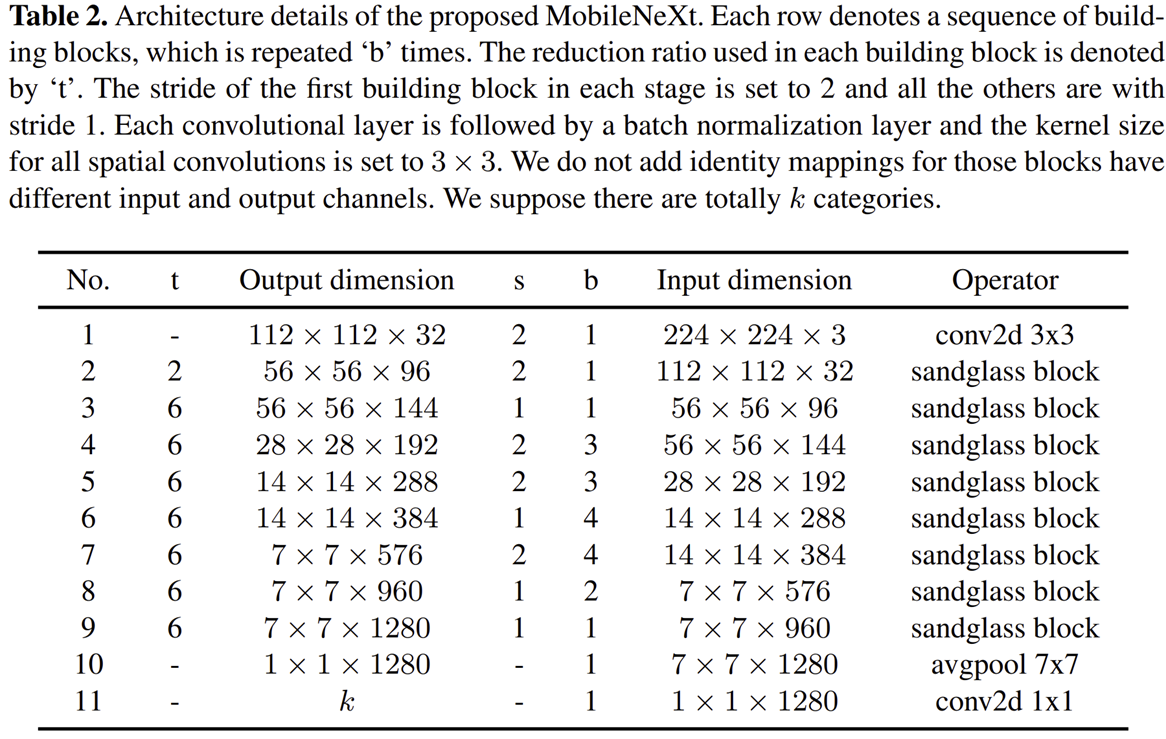
Experimental Results
1) Comparison with MobileNetV2

2) Comparison with other SOTA

3) Downstream Task - Object Detection

4) Network Architecture Searching with Sandglass Block

5) Ablation Study

