안녕하세요. 지난 포스팅의 [Transformer] TinyVit: Fast Pretraining Distillation for Small Vision Transformers (ECCV2022)에서는 새롭게 Fast Knowledge Distillation frame을 제안하여 보다 작은 규모의 Transformer인 TinyViT 만들 수 있게 되었습니다. 오늘은 주로 네트워크 구조 자체에 집중한 MobileViT를 소개하도록 하겠습니다.
MobileViT: Light-weight, General-purpose, and Mobile-friendly Vision Transformer
Light-weight convolutional neural networks (CNNs) are the de-facto for mobile vision tasks. Their spatial inductive biases allow them to learn representations with fewer parameters across different vision tasks. However, these networks are spatially local.
arxiv.org
Background
기본적으로 저희가 보았던 Transformer 기반 모델들 (ViT, DeiT, SwinT, CvT, ...)은 모두 너무 큰 모델 사이즈와 Pretraining 시 요구되는 대규모 데이터셋 (ImageNet-21K, JFT-300M)으로 인해 모바일 또는 IoT 계열에서 적합하지 않는다는 문제점이 있습니다. 이러한 문제점은 CNN에서 제안되었던 MobileNet과 마찬가지로 Lightweight Transformer를 만드는 것에 목표를 두게 되었습니다. 하지만, CNN과 다르게 Transformer는 컴퓨터 비전 분야에 필수적인 가정인 Inductive Bias가 CNN에 비해 부족하기 때문에 대용량의 데이터를 이용하여 이를 암시적으로 얻는 방법밖에 없습니다. 최근에는 이러한 문제점을 해결하기 위해 Convolution 연산을 결합한 하이브리드 구조도 제안되었죠. 대표적으로 PVT나 CvT와 같은 모델들이 있겠네요. 하지만, 이러한 모델들은 여전히 heavy-weight 구조와 data augmentation을 방식에 민감하게 성능이 달라진다는 문제점이 있었습니다.
본 논문에서는 이러한 문제를 해결하기 위한 새로운 Light-weight Transformer 구조인 MobileViT를 제안합니다. 네트워크 구조적 특이점은 Convolution을 함께 사용했다는 점에 PVT와 CvT와 유사해보일 수 있겠으나 이와 함께 Transformer Block에 입력하기 전에 특징 맵을 Unfold하여 spatial correlation을 잃지않게 만들어준다는 것이 중요합니다. 또한, 다양한 Transformer 모델에서는 학습 시 Multi-Scale Training Strategy를 사용하게 되는 데 본 논문에서는 효율적인 GPU 메모리 배분을 위한 DDP 방법론도 함께 제공합니다.
Mobile Vision Transformer (MobileViT)
1) Overall Framework

그림 1은 (a) 기존 ViT와 (b) 본 논문에서 제안하는 MobileViT 및 MobileViT Block의 전체적인 블록 다이어그램을 보여주고 있습니다. 어떤 부분에서 ViT와 달라졌는 지 차근차근 알아보도록 하겠습니다.
2) MobileViT Block
본 논문에서 제안하는 MobileViT Block의 목적은 더 적은 파라미터를 이용하여 지역적 특징과 전역적 특징을 동시에 모델링할 수 있도록 하는 것 입니다. 또한, 복잡하지 않은 단순한 data augmentation 만을 이용하여 높은 성능을 달성함과 동시에 Semantic Segmentation 및 Object Detection과 같은 downstream task에 성공적으로 적용하는 것을 목표로 합니다. 이를 위해 MobileViT Block은 다음과 같이 동작합니다.
STEP1. 입력 특징 맵 $\mathbf{X} \in \mathbb{R}^{H \times W \times C}$에 $n \times n$ 크기의 커널을 이용한 convolution과 pointwise convolution ($1 \times 1$)를 이용하여 Local Representation $\mathbf{X}_{L} \in \mathbb{R}^{H \times W \times d}$를 얻습니다. 이때, 처음에 사용된 $n \times n$ 크기의 커널을 이용한 convolution을 통해 특징 맵에 local spatial information을 인코딩시킬 수 있습니다. 그리고 pointwise convolution을 통해 high-dimensional space로 projection 시킬 수 있습니다. 즉, $C < d$라고 보시면 될 거 같습니다.
STEP2. $\mathbf{X}_{L} \in \mathbb{R}^{H \times W \times d}$를 $N$개의 non-overlapping flattened patch로 unfolding하여 $\mathbf{X}_{U} \in \mathbb{R}^{P \times N \times d}$를 얻습니다. 여기서 $P = wh$로 $w$와 $h$는 각각 쪼개진 패치들의 높이과 너비로 정의됩니다. 다음으로 $N = \frac{HW}{P}$는 전체 패치의 개수입니다. 이때, $n$은 STEP1에서 사용한 합성곱 연산의 커널 크기를 의미합니다. 실제 코드 상에서는 $n = 3$이라서 더 작은 $w = h = 2$로 설정한 것을 볼 수 있었습니다.
STEP3. 이제 각 패치 $p \in \{ 1, 2, \dots, P \}$에 대해서 패치 간 관계성 (inter-patch relationship)을 얻기 위해 다음과 같이 Transformer Block을 적용합니다.
$$\mathbf{X}_{G} = \text{Transformer} (\mathbf{X}_{U} (p)) \in \mathbb{R}^{P \times N \times d} $$
위 과정을 통해 global information까지 특징 맵에 인코딩할 수 있게 됩니다.
STEP4. 이제 다시 특징 맵 $ \mathbf{X}_{G} $을 원래 크기로 folding 시켜 $\mathbf{X}_{F} \in \mathbb{R}^{H \times W \times d}$를 얻습니다.
STEP5. 다음으로 STEP1에서 수행된 pointwise convolution으로 인해 전체 채널의 개수가 $d$만큼 증가하였으므로 $C$로 다시 줄여줍니다. 그리고 마지막으로 입력 특징 맵 $\mathbf{X}$와 concatenation한 뒤 $n \times n$ 크기의 커널을 가진 convolution을 통해 최종 특징 맵을 얻게 됩니다.

그림 4는 MobileViT의 Receptive Field를 보여주고 있습니다. 결국 해당 블록을 사용하게 되면 빨간색 픽셀을 중심으로 모든 영역을 커버하여 학습할 수 있다는 것을 알려주고 있습니다.
- Relationship to Convolution: 일반적인 convolution 연산은 Unfolding + Matrix Multiplication + Folding의 연산 순으로 진행된다고 합니다. 이 과정은 MobileViT에서도 동일하게 진행되는 것을 볼 수 있죠. 하지만, Matrix Multiplicatoin을 Transformer Block으로 변경하여 global processing을 가능하게 만들었습니다. 이러한 특징은 Transformer를 마치 (like) convolution 연산처럼 활용했다는 점에서 Transformer as Convolution이라고 부르게 되었습니다.
3) MobileViT Architecture
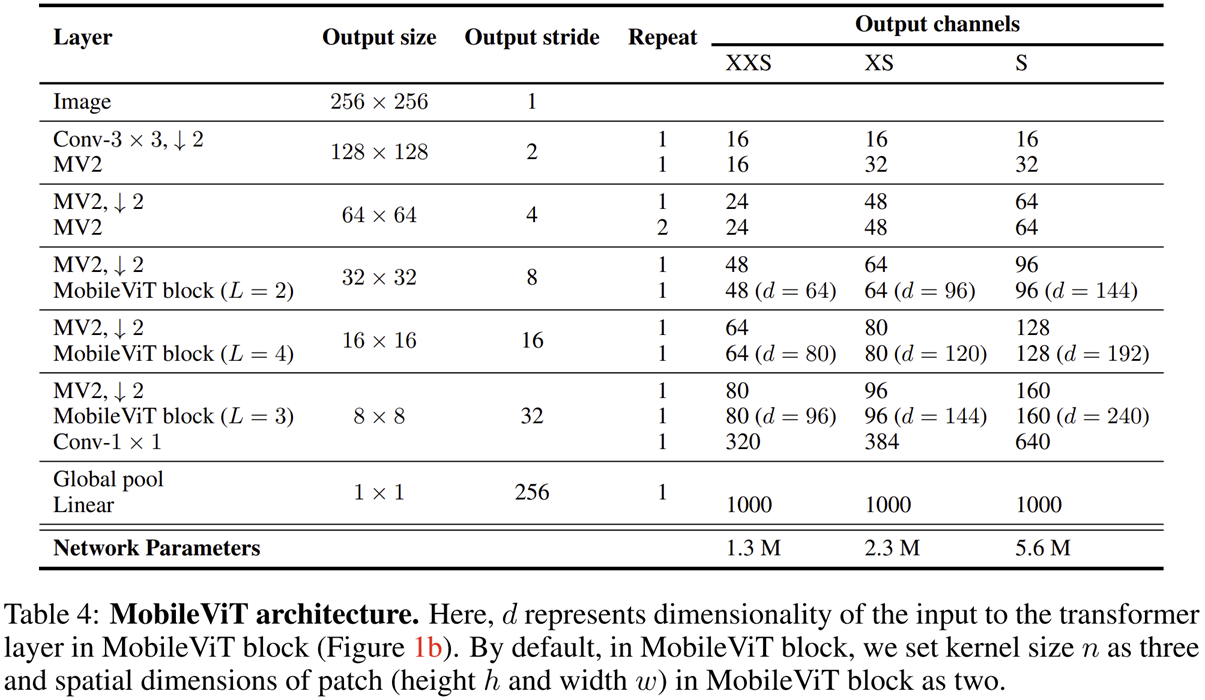
그림 1 (b)에서 볼 수 있지만 MobileViT는 모든 계층에서 MobileViT Block을 활용하지는 않았습니다. 아무래도 Transformer Block에 내재된 Self-Attention 연산이 해상도의 제곱만큼 복잡도가 요구되기 때문이겠죠. 따라서, 초기 계층에서는 MobileNetV2 (MV2)에서 사용한 블록 구조를 활용해주고 Stage 3부터 MobileViT Block을 활용하기 시작합니다. Stage 3, Stage 4, Stage 5에서는 각각 MobileViT Block을 $L = \{ 2, 4, 3 \}$번만큼 반복하여 사용한 것을 볼 수 있죠. 그리고 여타 다른 Transformer 모델과 마찬가지로 모델의 규모에 따라 MobileViT-XXS, MobileViT-XS, MobileViT-S를 설계하였습니다. 각각 달라지는 것은 내부 hidden dimension $d$를 각 Stage별로 어떻게 설정하는 지에 따라서 달라집니다. 그리고 각 스케일별 파라미터는 1.3M, 2.3M, 5.6M으로 굉장히 적은 양의 파라미터만 필요한 것을 볼 수 있죠.
4) Multi-Scale Sampler For Training Efficiency
이번에는 Multi-Scale Training Strategy를 이용하여 학습 시 효율적인 GPU 메모리 배분을 위한 DDP 방법론을 제시합니다. 먼저 학습하게 되는 다양한 입력 해상도 집합 $\mathcal{S} = \{ (H_{1}, W_{1}), (H_{2}, W_{2}), \dots, (H_{n}, W_{n}) \}$이 주어졌다고 가정하겠습니다. 이때 입력 해상도 집합 $\mathcal{S}$는 내부적으로 오름차순 정렬되었으며 $(H_{n}, W_{n})$을 학습하게 되는 가장 큰 해상도를 의미하게 됩니다. 그리고 $t$번째 training iteration에서 $(H_{t}, W_{t}) \in \mathcal{S}$를 선택하여 학습하게 될 때 사용되는 배치 사이즈 $b_{t} = \frac{H_{n}W_{n}b}{H_{t}W_{t}}$로 설정하게 됩니다. 여기서 $b$는 미리 설정된 배치 사이즈라고 가정하겠습니다. 그러면 $(H_{t}, W_{t})$가 작게 되면 $b_{t}$는 커지게 되어 더 많은 배치 사이즈를 가지고 학습하게 됩니다. 따라서 학습 속도가 빨라지겠죠. 반대로 $(H_{t}, W_{t})$가 커지게 되면 $b_{t}$는 작아지게 되어 더 적은 배치 사이즈를 가지고 학습하게 됩니다. 따라서, 한계 GPU 메모리 안에서 효율적으로 학습할 수 있게 될 겁니다.

그림 5는 본 논문에서 제시하는 Multi-Scale Sampler와 Standard Sampler 사이의 성능과 속도 비교를 하고 있습니다. 결과적으로 Multi-Scale Sampler를 사용하게 되면 전체 Update가 수가 줄어들기 때문에 Epoch 시간이 현저하게 감소하게 됩니다. 또한 성능도 배치 사이즈를 유동적으로 관리하기 때문에 0.5% 정도 향상되었다고 하네요.
Experiment Results
1) Image Classification (ImageNet-1K)



2) Object Detection (COCO)

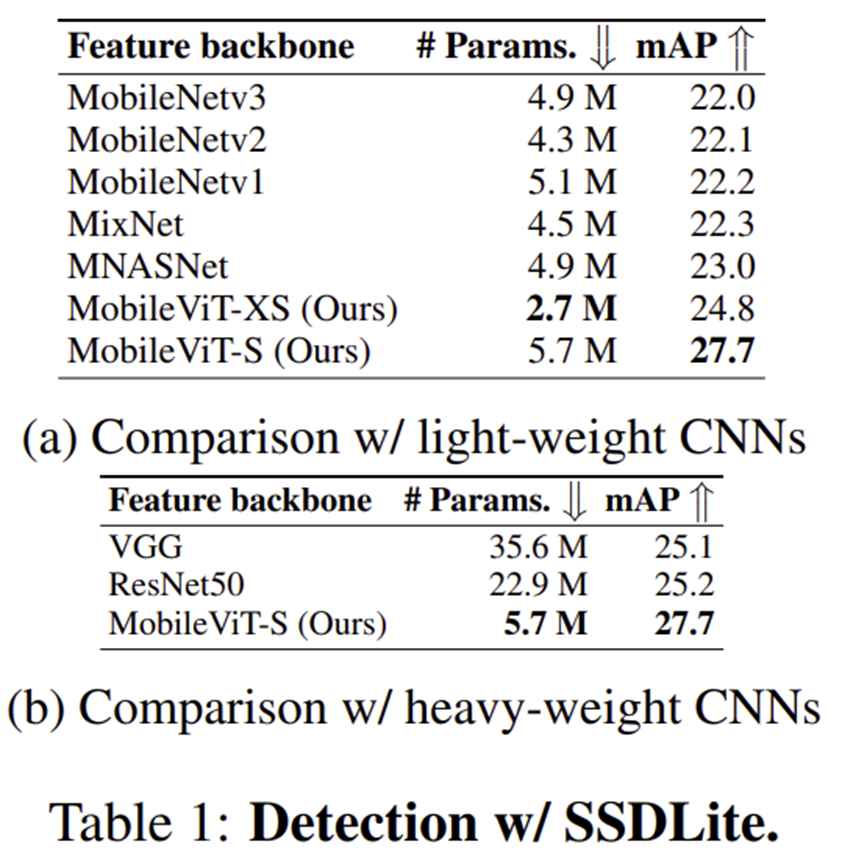

3) Semantic Segmentation (PASCAL VOC)


4) Efficiency Analysis

