안녕하세요. 지난 포스팅의 [Transformer] MobileViT: Light-weight, General Purpose, and Mobile-friendly Vision Transformer (ICLR2022)에서는 TinyViT와 유사하게 효율성을 강조한 Transformer인 MobileViT에 대해서 알아보았습니다. 결국 Transformer를 작은 규모에서 충분히 좋은 성능을 이끌어내기 위해서는 convolution이 가진 inductive bias를 최대한 활용해야한다는 공통점이 있었죠. 오늘은 이러한 중요성을 바탕으로 설계되어 convolution과 self-attention을 결합한 CoAtNet에 대해서 소개하도록 하겠습니다.
CoAtNet: Marrying Convolution and Attention for All Data Sizes
Transformers have attracted increasing interests in computer vision, but they still fall behind state-of-the-art convolutional networks. In this work, we show that while Transformers tend to have larger model capacity, their generalization can be worse tha
arxiv.org
Background
지금까지 저희는 굉장히 많은 종류의 CNN 및 ViT 계열 모델들을 보았습니다. 그 중에서도 ViT의 경우에는 CNN에 비해 inductive bias가 부족하기 때문에 엄청난 양의 데이터셋을 필요로 하게 되어 그만큼 높은 연산량이 요구된다는 문제점이 꾸준히 제기되어왔습니다. 이러한 문제를 해결하기 위해 CvT, LeViT, T2T와 같은 ViT 계열 모델들에서는 내부적으로 convolution 연산을 Transformer 구조에 적용하여 inductive bias를 추가하는 방향으로 발전되었습니다.
본 논문에서는 convolution 연산과 self-attention을 융합하기 위해 체계적인 방식으로 실험을 진행하였습니다. 특히, 본 논문에서는 모델의 Generalization Ablity와 Model Capacity의 측면에서 모델의 전체적인 레이아웃을 결정하였습니다. 이를 기반으로 convolution과 self-attention을 결합한 Depthwise Convolution and Self-Attention Network (CoAtNet)은 서로 다른 데이터셋 사이즈를 가지는 경우에도 CNN 기반 모델들과 거의 동등한 정도의 성능을 내게 되었습니다.
Convolution and Self-Attention Network (CoAtNet)
본 논문의 핵심은 어떻게 최적으로 convolution과 transformer의 장점을 결합한 모델을 만들것이냐 입니다. 이를 위해 본 논문에서는 다음과 같이 두 가지 질문을 던집니다.
(a) How to combine the convolution and self-attention within one basic computational block?
(b) How to vertically stack different types of convolutional blocks together to form a complete network?
(a) 질문은 하나의 연산 블록에 convolution 연산과 self-attention을 동시에 적용하는 방법에 대한 질문으로 단일 블록에 한정되어 있습니다. (b) 질문은 이러한 설계된 블록을 기반으로 모델의 레이아웃을 짤 때 어떤식으로 설계해야 좋을까에 대한 질문으로 모델의 전체 구조로 확장됩니다.
1) Merging Convolution and Self-Attention
MobileNet V2와 EfficientNet의 등장으로 많은 논문들에서 MBConv라는 convolution block을 활용합니다. MBConv의 핵심은 depthwise convolution을 활용하여 feature map의 spatial interaction을 추출하는 것에 있습니다. 본 논문에서도 MBConv를 핵심 블록으로 사용하게 되는 데 이에 대한 이유로는 두 가지가 있습니다. Transformer의 핵심 연산은 FFN입니다. 첫번째는 두 연산 모두 "inverted bottleneck"의 형태를 띄고 있습니다. 쉽게 말하면 채널 개수를 줄였다가 늘리는 일반적인 resnet block이 아니라 반대로 채널 개수를 늘렸다고 줄이는 inverted 구조를 가지는 bottleneck 형태이죠. 두번째는 depthwise convolution과 self-attention 모두 pre-defined receptive field에서 차원 당 가중치의 합으로 표현될 수 있습니다. 이러한 구조적, 연산적 특성으로 인해 본 논문에서는 MBConv에 집중하기로 하죠.
먼저, MBConv와 Self-Attention을 단순하게 수식으로 정리하면 다음과 같습니다.
$$y_{i} = \sum_{j \in \mathcal{L}(i)} w_{i - j} \odot x_{j} - (1)$$
$$y_{i} = \sum_{j \in \mathcal{G}} \frac{\text{exp} (x_{i}^{T} x_{j})}{\sum_{k \in \mathcal{G}} \text{exp} (x_{i}^{T} x_{k})} x_{j} - (2) $$
(1)번 식은 MBConv를 나타낸 것으로 depthwise convolution을 의미합니다. 여기서 공통적으로 $x_{i}, y_{i} \in \mathbb{R}^{D}$로 $i$번째 spatial position에 해당하는 입력 및 출력 텐션를 의미합니다. 그리고 $\mathcal{L} (i)$는 $i$번째 spatial position를 중심으로 하는 주변 영역을 의미합니다. 예를 들어 $3 \times 3$ 크기의 커널을 사용하는 것과 동일하다고 생각하시면 될 거 같네요! (2)번 식은 self-attention을 수식적으로 표기하였습니다. 여기서 $\mathcal{G}$는 입력 텐션의 global spatial space를 의미합니다. 이제 두 연산을 하나로 결합하기 전에 기본적으로 두 연산이 가지는 장단점을 분석해보도록 하겠습니다.
- MBConv의 입력 텐선와 무관하게 가중치는 학습가능하게 설계 (input-independent parameter)되어 있지만 self-attention의 가중치는 feature map의 pixel과 pixel 사이의 관계성을 기반으로 설계되어 input에 따라 동적인 attention mask가 생성 (input-dependent parameter) 됩니다. 따라서, self-attention은 서로 다른 spatial position 사이의 복잡한 관계성을 MBConv보다 더 잘 이해할 수 있습니다. 하지만, 데이터가 제한되어 적은 경우 과적합 (overfitting)의 가능성이 높죠.
- MBConv는 특정 spatial position $(i, j)$가 주어졌을 때 가중치 $w_{i - j}$는 상대적인 위치 차이 ($i - j$)만 고려합니다. 이는 흔히 convolution의 inductive bias 중 하나인 translation equivalence에 해당하죠. 이러한 이유로 convolution 연산은 Transformer에 비해 적은 데이터셋에서도 generalizability가 높은 것이죠. ViT는 absolution positional embedding을 사용하지만 이는 단순히 패치간 관계성만 이해하기 때문에 convolution 연산보다는 상대적으로 약한 inductive bias를 가지게 됩니다.
- 두 연산은 가장 큰 차이는 바로 receptive field입니다. MBConv에서는 제한된 영역 $\mathcal{L} (i)$ 내에서만 관계성을 고려하는 데 반해 Self-Attention의 경우 global spatial space $\mathcal{G}$를 고려하죠 따라서, Transformer 기반 모델들은 convolution 연산에 비해 더 큰 receptive field를 제공하기 때문에 더 많은 정보를 추출할 수 있고 이는 modal capacity가 증가하게 되는 이유가 될 수 있습니다. 하지만, 문제점은 receptive field가 커질 수록 self-attention에서 요구되는 연산량이 feature map의 spatial resolution의 제곱만큼 커진다는 것이죠.

지금까지 내용을 토대로 표로 정리하면 표 1과 같습니다. 결과적으로 저희가 원하는 모델은 3가지 property들을 동시에 만족해야하죠. 이를 위해 본 논문에서 선택한 방법은 global static convolution kernel을 adaptive attention matrix에 합쳐주는 것이죠. 이는 매우 단순하지만 3가지 property들을 만족해주는 아주 효율적인 방법입니다. 다만 여기서, global static convolution kernel을 adaptive attention matrix에 더해줄 때 softmax 연산 이전 (pre)에 할지 또는 이후 (post)에 할지로 나뉘게 됩니다.
$$y_{i}^{\text{pre}} = \sum_{j \in \mathcal{G}} \left( \frac{\text{exp} (x_{i}^{T} x_{j} + w_{i - j})}{\sum_{k \in \mathcal{G}} \text{exp} (x_{i}^{T} x_{k} + w_{i - k})} \right) x_{j} $$
$$y_{i}^{\text{post}} = \sum_{j \in \mathcal{G}} \left( \frac{\text{exp} (x_{i}^{T} x_{j})}{\sum_{k \in \mathcal{G}} \text{exp} (x_{i}^{T} x_{k})} + w_{i - j} \right) x_{j} $$
여기서 효과 측면에서 $y_{i}^{\text{pre}}$의 경우 pixel-pixel의 상대적 연관성이 $w_{i - j}$를 더해줌으로써 추가되고 어텐션 가중치 $A_{i, j}$가 input-dependent로 바뀌게됩니다. 다만, self-attention의 특성 상 global spatial space $\mathcal{G}$를 고려하기 때문에 연산량을 어느정도 보존해주어야합니다. 이를 위해 본 논문에서는 $w \in \mathbb{R}^{\mathcal{O}(|\mathcal{G}|)}$와 같이 벡터가 아닌 스칼라의 형태로 가지게 만들어줍니다. 이를 통해, 모든 $(i, j)$에 대해 $w_{i - j}$는 pairwise dot-product attention에 의해 계산되기 때문에 계산비용이 크게 감소합니다.
즉, Transformer Block에 pre-normalization relative attention을 추가하여 만든 모델이 바로 CoAtNet 라고 이해하시면 될 거 같습니다! 이를 통해, 저희는 처음에 언급한 질문 (a)에 대한 답변을 완료하였습니다. 이제부터는 해당 블록을 이용해 어떻게 모델을 설계할 지 생각해봐야합니다. (질문 (b))
2) Vertical Layout Design
Convolution과 Transformer의 장점을 모았다고 하더라도 모델의 구조에 따라 전체적인 generalization ability와 model capacity는 달라지게 됩니다. 또한, 기본적으로 해당 모델은 Transformer 기반이기 때문에 내재된 Self-Attention의 특성 상 복잡도는 입력 feature map의 resolution에 quadratic하게 늘어납니다. 그렇다면 이를 줄이는 방법을 있을까요? 본 논문에서는 3가지의 방법을 고려해본다고 합니다.
Option A) 입력 feature map의 spatial size를 downsampling 한 뒤 global receptive field를 활용하기 위한 Transformer 블록을 적용한다.
Option B) Global receptive field는 전체 연산량을 너무 많이 차지하니 local field로 제한하여 local attention의 형태로 설계하자.
Option C) Softmax Attention Mechanism를 spatial size에 대해 linear complexity를 가지는 다른 Self-Attention으로 바꾼다.
본 논문에서는 실험 결과를 보여주지는 않았지만 Option C)는 성능이 안좋아 폐기했다고 합니다. 그리고 Option B) 같은 경우에는 global spatial space를 활용하지 못하기 때문에 model capacity가 훼손될 가능성이 있어 기존의 global attention의 장점이 없어지는 문제가 있습니다. 이러한 문제로 인해 본 논문에서는 Option A)를 이용해서 복잡도를 줄이고자 합니다.
그렇다면 얼마나 downsampling을 하고 Transformer 블록을 적용하는 게 generalization ability와 model capacity 측면에서 효율적일까요? 본 논문에서는 이를 위한 실험을 진행합니다. $\text{ViT}_{\text{Rel}}$은 Relative Attention을 적용한 Transformer이라고 하겠습니다. 그리고 convolution과 Transformer를 혼합하여 사용한다고 했을 때 각 스테이지의 이름을 $S_{0}, S_{1}, S_{2}, S_{3}, S_{4}$라고 하겠습니다. 여기서 $S_{0}$는 단순히 2개의 convolution 연산으로 이루어진 Stem Block입니다. 그리고 $S_{1}$은 MBConv와 SE Block이 결합되었습니다. 나머지들 ($S_{2}, S_{3}, S_{4}$)은 MBConv 또는 Transformer로 정의됩니다. 따라서, $S_{0}$를 제외하고 작성했을 때 총 4가지의 변형 (C-C-C-C, C-C-C-T, C-C-T-T, C-T-T-T)이 존재합니다. 여기서 C는 Convolution을 사용한 경우를 의미하고 T는 Transformer를 사용한 경우를 의미합니다.
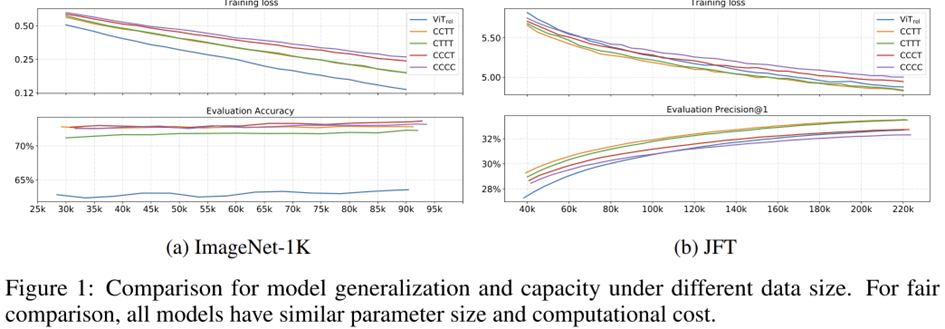
본 논문에서는 Generalization ability와 Modal capacity 측면에서 전체 구조의 성능을 분석합니다.
Generalization ability는 쉽게 말해 과적합의 정도라고 볼 수 있습니다. 이는 training loss와 evaluation accuracy 사이의 gap으로 어느정도 유추할 수 있죠. 이를 기반으로 했을 때 그림 1 (a)의 결과는 다음과 같습니다.
$$\text{C-C-C-C} = \text{C-C-C-T} > \text{C-C-T-T} > \text{C-T-T-T} >> \text{ViT}_{\text{Rel}}$$
Model capacity는 대규모 데이터셋으로 훈련했을 때 얼마나 잘 fit할 수 있는지로 측정할 수 있습니다. 이를 위해 본 논문에서는 google에서만 사용할 수 있는 JFT-300M을 이용해서 실험을 진행하였습니다. 이를 기반으로 했을 때 그림 1 (b)의 결과는 다음과 같습니다.
$$\text{C-C-T-T} = \text{C-T-T-T} > \text{ViT}_{\text{Rel}} > \text{C-C-C-T} > \text{C-C-C-C}$$

결국 $ \text{C-C-T-T} $와 $ \text{C-T-T-T} $가 Generalization ability와 Model capacity 측면에서 어느정도 성능이 있음을 확인하였습니다. 최종적으로 레이아웃을 사용할 지 결정하기 위해 Transferability를 측정하였습니다. 이는 JFT-300M에 학습된 모델을 ImageNet-1K에 fine-tuning했을 때 실험결과로 보여줍니다. 결과적으로 $ \text{C-C-T-T} $가 더 높은 성능을 가지므로 해당 레이아웃으로 다음과 같이 모델 설계을 하였습니다.



Experiment Results

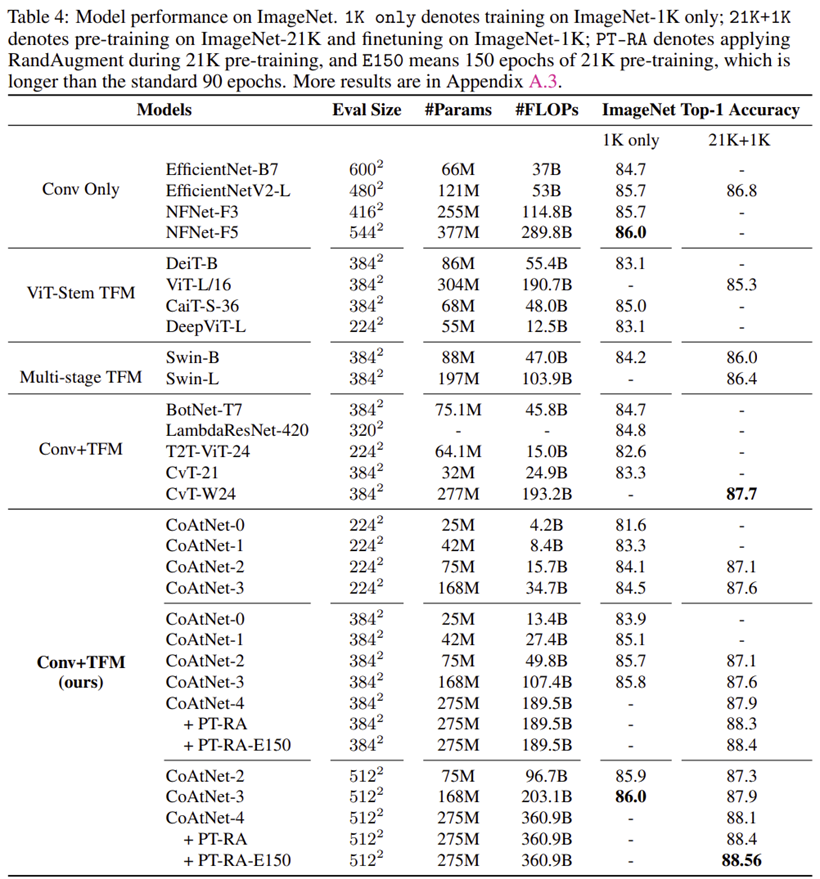
1) ImageNet-1K Classification


2) Ablation Study
2-1) Relative Attention

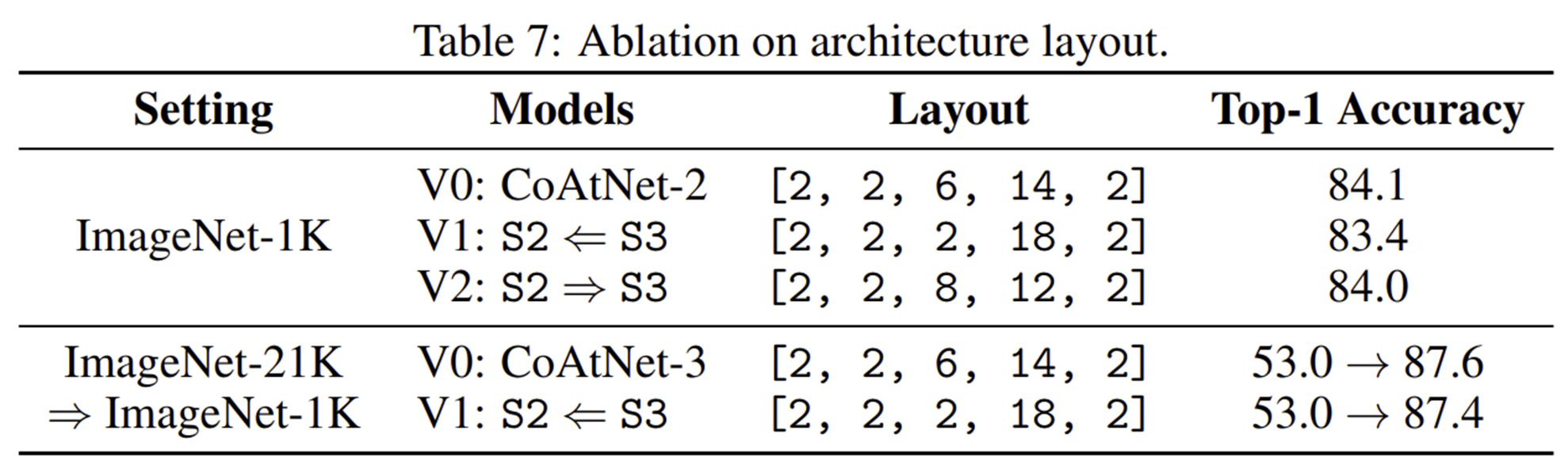
2-2) Architecture Layout
2-3) Head Size & Normalization Type

