안녕하세요. 지난 포스팅의 [IC2D] CONTAINER: Context Aggregation Network (NIPS2021)에서는 Transformer, Convolution, MLP-Mixer 사이의 관계성을 수학적으로 분석하고 이를 하나의 모델로 결합한 CONTAINER라는 모델에 대해서 소개하였습니다. 결국, CoAtNet과 마찬가지로 Self-Attention과 Convolution을 각각 적용한 뒤 두 특징을 Aggregation하는 것이 핵심이였죠. 오늘은 잠시 주제를 바꾸어 Inference Speed를 향상시키기 위해 제안된 Resolution Adaptive Network (RANet)에 대해서 소개시켜드리도록 하겠습니다.
Background
지금까지 저희가 보았던 수많은 모델들은 대부분 단순히 모델의 복잡도 (깊이, 너비, cardinality, scale 등)을 향상시킴으로써 성능을 최대한 올리는 것을 목표로 하였습니다. 하지만 성능을 강조한 모델들은 현재 다양한 어플리케이션에서의 활용이 제한된다는 문제점이 있습니다. 이러한 문제를 해결하기 위해 MobileNetV1을 시작으로 수많은 효율성을 강조한 모델들이 제안되었습니다. 대표적으로 MobileNetV2, MobileNetV3, ShuffleNetV1, ShuffleNetV2, EfficientNet, CondenseNetV1, CondenseNetV2 등이 있죠. 또는 Network Architecture Searching (NAS) 기법을 적용한 NASNet과 PNASNet도 효율적으로 동작할 수 있게 만들었습니다. 이러한 모델들은 모두 Light-weight 구조를 위한 모델들이라고 볼 수 있죠. 물론, 효율적인 모델 자체를 설계하는 것도 한가지 방법이 될 수 있지만, 일단 대규모 모델을 만들어놓고 이를 효율적으로 만드는 Network Pruning, Weight Quantization, Adaptive Inference 기법 등을 적용할 수 있습니다.
본 논문에서는 이 중에서 Adaptive Inference을 통한 효율적인 모델 설계를 수행하였습니다. 핵심은 입력 인스턴스 별로 어떤 입력이 "쉬운" 데이터 샘플이고 "어려운" 데이터 샘플 인지를 구분하는 것 입니다. 그리고 만약 쉬운 샘플이라면 더 복잡한 모델 흐름으로 적용하지 않고 그대로 출력을 내보내고 어려운 샘플이라면 더 복잡한 모델 흐름으로 연결하여 정교한 특징을 추출할 수 있도록 도와주게 됩니다. 이러한 특성은 아래의 그림에서 더욱 자세하게 볼 수 있습니다. 본 논문에서는 이러한 구조를 가진 새로운 모델 형태인 Resolution Adaptive Network (RANet)을 제안하였습니다. 이와 같은 모델의 구조는 이전의 DenseNet과 동일한 형태를 가지지만 이전 light-weight 모델과 같은 model-centric이 아닌 데이터 샘플에 집중하기 때문에 data-centric한 방법이라고 볼 수 있습니다.

Method
1) Adaptive Inference Setting
본 논문에서는 먼저 다음과 같이 Adaptive Inference를 위한 모델 셋팅을 설계합니다.
$$\mathbf{p}_{k} = f_{k} (\mathbf{x}; \theta_{k}) = [p^{k}_{1}, \dots, p^{k}_{C}] \in \mathbb{R}^{C}$$
여기서 $\theta_{k}$는 $k$번째 classifier $f_{k} (\cdot)$의 가중치로 정의됩니다. 따라서, 각각의 분류기는 모두 서로 다른 가중치로 설정되어 있는 것을 알 수 있죠. 그리고 $p^{k}_{c}$는 $c$번째 클래스에 대응되는 예측에 대한 신뢰도로 볼 수 있습니다.
기본적으로 Adaptive Inference에서는 주어진 입력 데이터 샘플의 복잡도에 따라 자원량을 다르게 할당해줍니다. 본 논문에서는 데이터 샘플의 복잡도를 정량적으로 해석하기 위해 softmax output의 신뢰도를 기반으로 decision basis를 설정합니다. 이 과정을 수식으로 작성하면 다음과 같습니다.
$$\begin{cases} k^{*} = \text{min} \{ k | \text{max}_{c} p^{k}_{c} \ge \epsilon \} \end{cases}$$
여기서 $\epsilon$은 임계점으로 분류기의 성능과 효율성 사이의 trade-off를 부여합니다. 만약 높은 $\epsilon$을 사용한다고 가정하면 이는 높은 신뢰도를 보장하기를 원하는 것과 동일하기 때문에 상대적으로 높은 정확도를 얻을 수 있지만 그만큼 자원을 많이 소비하게 될 겁니다. 반대로 작은 $\epsilon$을 사용한다면 낮은 신뢰도를 보장하는 대신 자원을 훨씬 덜 소비하게 될테죠.
2) Overall Architecture

그림 2는 RANet의 전체적인 구조를 보여줍니다. 총 3개의 핵심적인 서브 모듈로 구성되어 있죠. 각각 Initial Layer, Sub-Network, Classifier입니다.
2-1) Initial Layer
본 논문의 제목인 "Resolution Adaptive"라고 불릴 수 있는 핵심적인 구조가 여기에 포함되어 있습니다. 입력 영상은 그림 2와 같이 총 $S$개의 스케일 branch로 구성된 Initial Layer를 통과하여 $H$개의 base feature를 만들어줍니다. 그리고 이 단계에서 사용되는 Convolution 계층은 두 가지로 Regular-Conv Layer와 Strided-Conv Layer가 있습니다. 두 계층의 가장 큰 차이점은 입출력 특징맵의 해상도가 유지되는 지입니다. 위 그림에서는 빨간색 화살표가 Regular-Conv Layer이고 파란색 화살표가 Strided-Conv Layer로 정의됩니다. 여기서 해상도를 줄이기 위해 stride가 2인 Strided-Conv Layer를 사용했다고 하네요. 그리고 Regular-Conv Layer는 Bottleneck 구조가 포함되어 있습니다.
2-2) Sub-Networks with Different Scales
Initial Layer로부터 추출된 $S$개의 특징 맵 뭉치들은 이제 각 scale에 배정된 Sub-Network에 입력됩니다. 하지만, 여기서 중요한 것은 만약 낮은 해상도에서 얻은 예측 결과가 낮은 신뢰도를 보일 때 더 높은 해상도의 계층에서 진행이 됩니다. 다만, 이전 낮은 해상도에 대응되는 Sub-Network의 특징을 현재 높은 해상도의 Sub-Network로 특징을 결합시켜주어 예측 신뢰도를 높힐 수 있도록 도와줍니다. 하지만, 가장 낮은 해상도를 가지는 마지막 Sub-Network에서는 결합되는 특징이 없기 때문에 따로 설명을 하도록 하겠습니다.
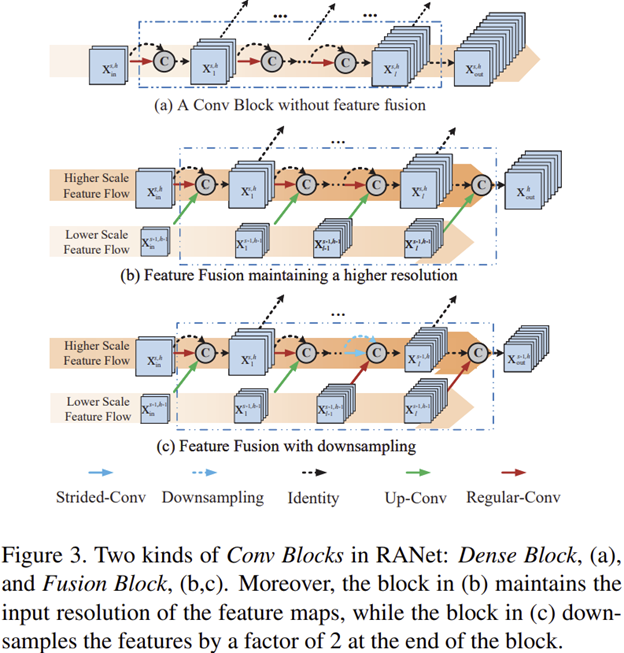
Sub-Network 1 with Input $\mathbf{x}^{1, 1}_{0}$ 해당 계층은 가장 낮은 해상도를 입력으로 받고 기본적으로 $l$개의 Dense Block을 가질 수 있도록 설계가 되었습니다. 그림 3 (a)에서 그 예시를 볼 수 있습니다. 그리고 만약, 해당 흐름에서 결과가 신뢰도가 너무 낮다면 더 높은 해상도 흐름으로 그 특징 맵들이 재사용되어 더 높은 해상도의 예측 신뢰도가 향상될 수 있도록 도와줍니다.
Sub-Network on Larger-scale features 해당 계층들은 낮은 해상도의 특징 맵들을 fusion하는 모듈이 포함되어 있습니다. 다만, 이 과정에서 본 논문에서는 그림 3 (b)와 (c) 같이 서로 다른 구조를 추가적으로 제안합니다. 기본적으로 두 구조 모두 입력되는 특징들을 모두 concat을 취한 뒤 convolution 연산을 하는 과정은 동일합니다. 그리고 Sub-Network $h - 1$이 총 $b_{h - 1}$개의 블록을 가지고 있다고 가정하면 Sub-Network $h$의 처음 $b_{h - 1}$개의 블록에서 fusion module이 적용됩니다. 그리고 나머지 블록들은 일반적인 Dense Block을 차용하죠. 그리고 그림 3 (b)와 (c)는 fusion module에서 연산량을 감소하기 위해 downsampling을 적용하는 지가 그 핵심차이라고 볼 수 있습니다.
2-3) Transition Block
해당 블록은 DenseNet과 동일한 형태로 각 Sub-Network에 모두 포함되어 있는 블록입니다. $1 \times 1$ convolution + Batch Normalization + ReLU로 구성되어 있는 블록으로 dense하게 연결된 특징 맵들의 복잡도를 줄이고 non-linearity를 추가적으로 부여하여 효율성을 증가시켜줄 수 있습니다.
2-4) Classifier and Loss Function
Classifier의 경우 모든 계층에서 적용되지는 않고 각 Sub-Network에서 마지막 몇 블록에서만 적용해줍니다. 그리고 학습 단계에서는 전체 네트워크가 가중치가 업데이트가 되어야하기 때문에 Sub-Network 1부터 Sub-Network $H$까지 각각 예측결과를 뽑은 뒤 각 classifier에 대해서 cross-entropy를 적용하여 손실함수를 계산한 뒤 파라미터 업데이트를 수행합니다.
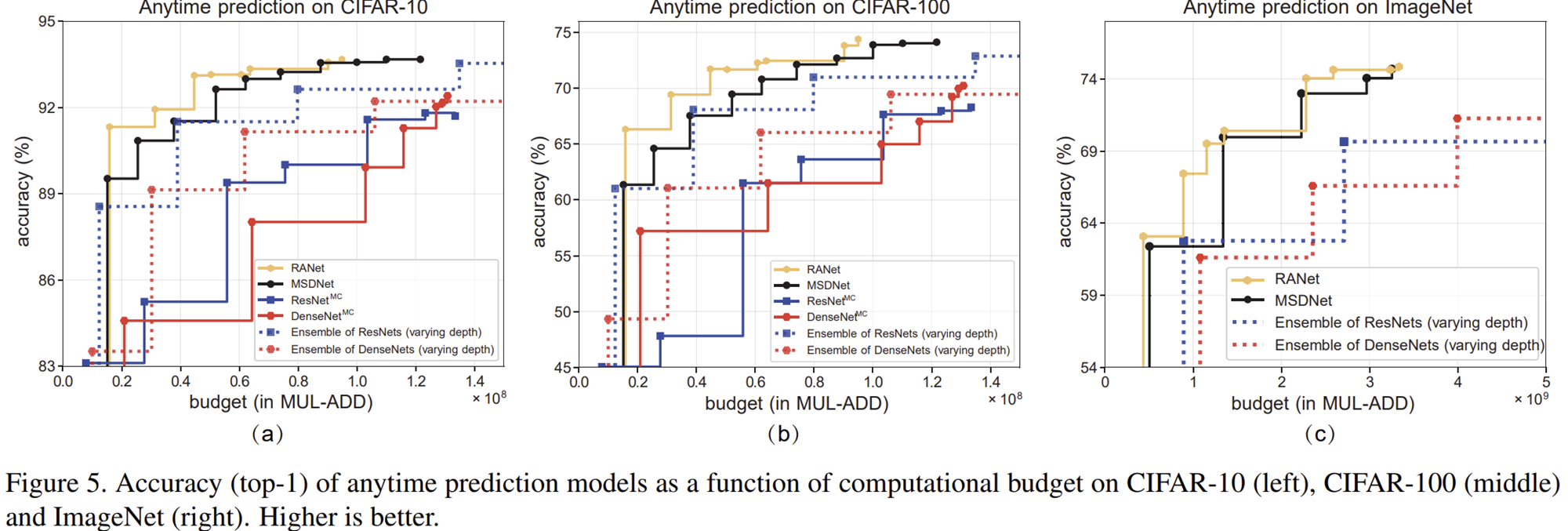
Experimental Results