안녕하세요. 지난 포스팅의 [IC2D] Attentional Feature Fusion (WACV2021)에서는 다중 스케일 특징 맵 간의 어텐션을 수행할 때 적응적으로 어텐션 맵을 추출하는 AFF 모듈에서 대해서 알아보았습니다. 오늘은 CVPR2020에 게재 승인된 GhostNet에 대해서 알아보도록 하겠습니다.
Background
지금까지 제안된 효율성을 강조한 다양한 모델들을 보았습니다. 가장 대표적으로 MobileNet, ShuffleNet, CondenseNet, NASNet 등이 있었죠. 이러한 모델들의 공통점은 모두 성능을 최대한 보존하면서 파라미터 개수나 latency 및 FLOPs를 줄임으로써 스마트폰 또는 자율주행 자동차에 모델을 사용할 수 있게 만드는 것을 목표로 하였습니다. 본 논문에서 제안된 GhostNet 역시 효율성을 강조한 모델입니다. 기존 모델들과는 전혀 다른 방식으로 접근하죠.
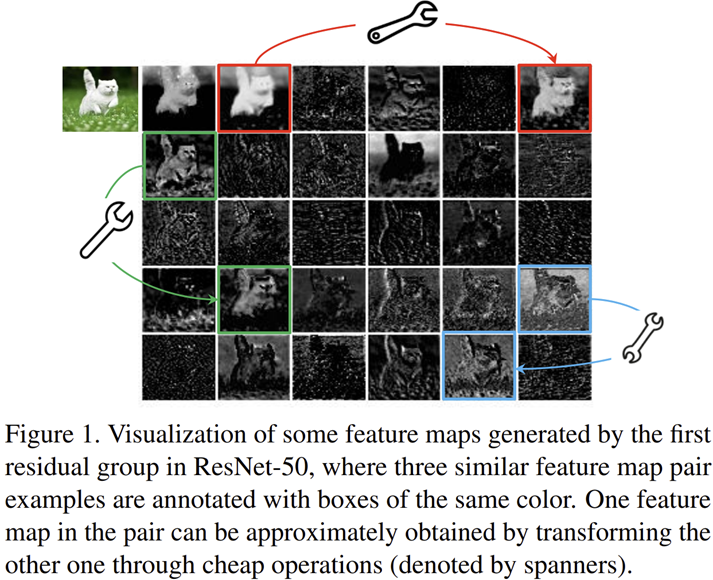
그림 1은 ResNet-50을 ImageNet으로 학습했을 때 얻은 중간 계층의 특징 맵들을 보여주고 있습니다. 위 그림에서 빨간색, 초록색, 파란색 사각형으로 쳐진 특징 맵들은 굉장히 유사한 구조를 지니고 있는 것을 볼 수 있죠. 즉, 딥 러닝 모델은 풍부하고 반복적인 특징 맵의 정보를 활용하여 입력 데이터에 대한 포괄적인 이해를 하는 것으로 이해할 수 있습니다. 이러한 해석을 통해 GhostNet에서는 256개의 특징 맵을 만들 때 64개의 대표 특징 맵만 만들어놓고 해당 특징 맵들에 단순한 선형 변환을 적용한다면 보다 파라미터 개수를 더 줄이면서 효율적으로 모델의 표현력을 늘릴 수 있음을 동기부여로 삼습니다.
Approach
1) Ghost Module for More Features
MobileNet과 ShuffleNet는 각각 Depthwise Separable Convolution 그리고 Shuffle Operation을 제안하여 모델의 효율성을 향상시킵니다. 하지만, 불필요한 $1 \times 1$ convolution (point-wise operation)의 반복적인 사용으로 인해 메모리와 FLOPs를 더 차지한다는 문제점이 있죠.
따라서, 본 논문의 저자는 $1 \times 1$ convolution 사용을 줄이는 방향으로 진행합니다. 이를 위해 기존의 convolution operation을 수식으로 작성하면 다음과 같습니다.
$$Y = X * f + b$$
여기서 $X \in \mathbb{R}^{c \times h \times w}$는 입력 특징 맵으로 해상도 $h \times w$ 그리고 채널 개수 $c$개를 가집니다. 그리고 $f \in \mathbb{R}^{c \times k \times k \times n}$는 convolution operation $*$를 위한 커널로 $k \times k$ 크기의 윈도우로 구성되고 $c$개의 채널을 이용하여 $n$개의 출력 채널을 만들게 됩니다. $Y \in \mathbb{R}^{h^{'} \times w^{'} \times n}$는 출력 특징 맵을 의미하죠. 마지막으로 $b$는 편향 (bias) 항을 의미합니다.
이와 같은 연산에서 FLOPs는 $n \cdot h^{'} \times w^{'} \times c \times k \times k$로 계산되죠. 여기서 FLOPs의 크기가 커지는 데 가장 많은 기여를 하는 항은 $n$과 $c$ 입니다. 각각 입력 및 출력 특징 맵의 채널 개수로 보통 64, 128, 256, 512, 1024 등 큰 값으로 정의되기 때문이죠. 여기서 핵심은 그림 1에서 보았던 중복된 특징 맵을 만들어주어야합니다. 만약, 256개의 특징 맵을 만들어야한다고 가정했을 때 64개만 만들고 단순한 선형 연산으로 192개의 특징 맵을 만들어준다면 해당 계층은 기존 convolution 연산보다 약 4배 감소한 FLOPs를 가지게 되는 것이죠!
이를 위해 Ghost Module에서는 기존의 convolution operation을 두 개의 단계로 나누어 줍니다. 첫번째 단계는 저희가 적용하던 convolution operation을 그대로 적용하면 됩니다. 다만 훨씬 더 적은 개수의 채널을 가지도록 설계하죠. 편의를 위해 편향 항을 생략하도록 하겠습니다.
$$Y^{'} = X * f^{'}$$
여기서 $f^{'} \in \mathbb{R}^{c \times k \times k \times m}$ 이고 $Y^{'} \in \mathbb{R}^{h^{'} \times w^{'} \times m}$의 크기를 가집니다. 또한 $m < n$임을 꼭 기억해주세요. 그리고 합성곱 연산을 통해 얻는 출력 특징 맵의 해상도를 유지하기 위해 stride, padding과 같은 하이퍼파라미터는 동일하게 셋팅했다고 가정하겠습니다. 이렇게 얻은 $m$개의 특징 맵을 intrinsic feature map이라고 하겠습니다.
다음 단계는 $m$개의 intrinsic feature map을 이용해서 $n$개의 특징 맵을 만들어주어야합니다. 이렇게 얻은 특징 맵을 ghost feature map이라고 하도록 하죠.
$$y_{ij} = \Phi_{i, j} (y^{'}_{i})$$
여기서 $i = 1, 2, \dots, m$이고 $j = 1, 2, \dots, s$로 $i$번째 intrinsic feature map $y^{'}_{i}$를 이용하여 $j$번째 선형 변환 $\Phi_{i, j} (\cdot)$을 적용하는 것을 볼 수 있습니다. 따라서, $y^{'}_{i}$는 1개 또는 여러 개의 ghost feature map $\{ y_{ij} \}_{j = 1}^{s}$를 가질 수 있습니다. 그리고 $\Phi_{i, s} (\cdot)$는 intrinsic feature map을 보존하기 위해 identity mapping으로 정의됩니다. 이렇게 얻은 feature map은 $Y = [y_{11}, y_{12}, \dots, y_{ms}]$로 총 $n = m \times s$개의 채널로 구성됩니다.
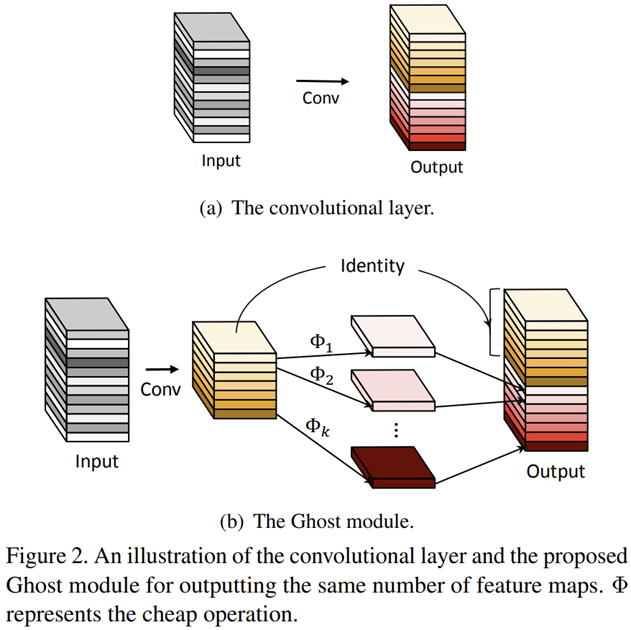
그림 2는 기존의 convolution operation과 Ghost Module 사이의 비교를 보여주고 있습니다.
2) Building Efficient CNNs
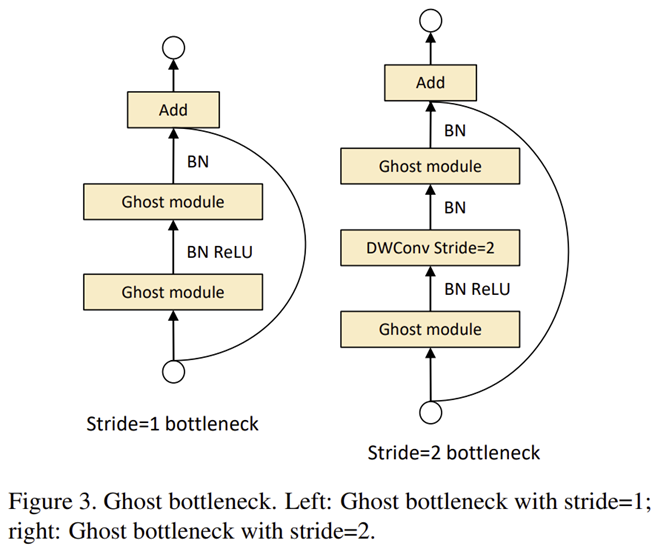
그림 3은 Ghost Module을 이용하여 구성한 Ghost Bottleneck을 보여주고 있습니다. 이와 같은 설계를 통해 다음과 같은 GhostNet을 설계하게 됩니다.
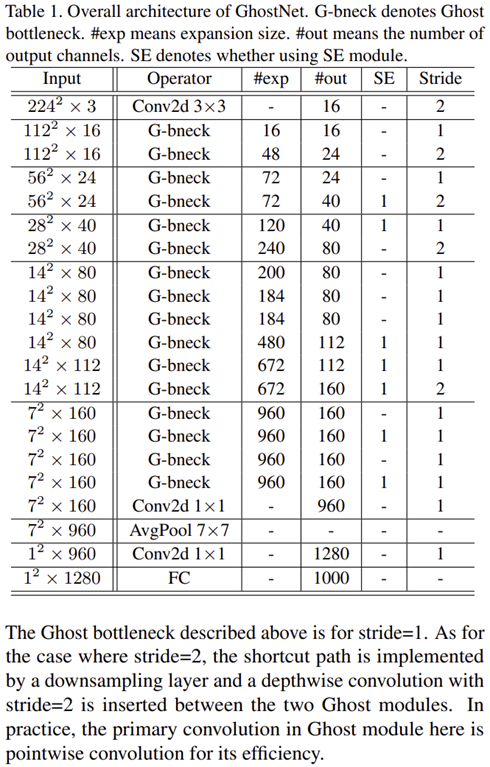
Experiment Results