안녕하세요. 지난 포스팅의 [IC2D] CondenseNet V2: Sparse Feature Reactivation for Deep Networks (CVPR2021)에서는 기존의 CondenseNet을 확장한 CondenseNet V2에 대해서 알아보았습니다. 핵심은 Sparse Feature Reactivation을 통해 DenseNet과 같이 모든 feature map들을 활성화하지 않고 feature importance를 기반으로 어떤 layer로부터 온 feature map들을 activation할 지 adaptive할 게 결정하는 것이였습니다. 오늘은 Attentional Feature Fusion (AFF)에 대해서 알아보도록 하겠습니다.
Background
지금까지 보았던 다양한 딥 러닝 모델들은 깊이를 더 깊게 하거나 너비를 넓게 만들거나 어텐션 매커니즘을 도입하여 CNN의 성능을 향상시켰습니다. 물론 이러한 방법들 역시 좋은 방법이지만 본 논문에서는 기존의 연구 흐름과는 다르게 feature fusion이라는 방식을 제안하고자 합니다. 그렇다고 해서 feature fusion 자체가 완전히 새로운 개념은 아닙니다. 예를 들어 InceptionNet, ResNet, FPN만 하더라도 다양한 feature map들을 하나의 feature map으로 fusion하는 과정이 존재하죠.
한편, SKNet과 ResNeSt에서는 동적으로 각 group 간 feature map들 간의 weighted averaging으로 feature fusion을 달성하였죠. 하지만 이러한 방법들은 동일한 스케일 간의 fusion만 고려하기 때문에 다중 스케일을 무시한다는 문제점이 있죠. 본 논문에서는 이러한 문제점을 지적하여 Attention Feature Fusion (AFF)를 제안합니다. 또한, AFF를 모듈화하여 반복적으로 적용할 수 있는 iterative AFF (iAFF)도 함께 제안하였습니다. 핵심은 Multi-Scale Channel Attention Module (MS-CAM)으로 다중 스케일 정보를 고려한 채널 어텐션을 통해 CNN의 표현력을 향상시킨 것 입니다.
Multi-Scale Channel Attention
1) Revisiting Channel Attention in SENet

채널 어텐션에 있어 가장 기본이 되는 SENet을 다시 한번 분석해보도록 하겠습니다. 입력 feature map $\mathbf{X} \in \mathbb{R}^{C \times H \times W}$가 주어졌을 때 채널 어텐션 맵 $\mathbf{w} \in \mathbb{R}^{C}$는 다음과 같이 얻을 수 있습니다.
$$\mathbf{w} = \sigma (\mathbf{g} (\mathbf{X})) = \sigma (\mathcal{B} (\mathbf{W}_{2} \delta (\mathcal{B} (\mathbf{W}_{1} (g(\mathbf{X}))))))$$
여기서 $\mathbf{g} (\mathbf{X}) \in \mathbb{R}^{C}$는 global feature context이고 $g(\mathbf{X}) = \frac{1}{H \times W} \sum_{i = 1}^{H} \sum_{j = 1}^{W} \mathbf{X}_{[:, i, j]}$로 Global Average Pooling (GAP)로 정의됩니다. 그리고 $\delta (\cdot)$과 $\mathcal{B} (\cdot)$은 각각 ReLU와 배치 정규화 (Batch Normalization)을 의미하죠. 마지막으로 $\sigma (\cdot)$은 시그모이드 함수로 정의되고 $\mathbf{W}_{1} \in \mathbb{R}^{\frac{C}{r} \times C}, \mathbf{W}_{2} \in \mathbb{R}^{C \times \frac{C}{r}}$은 각각 Fully-Connected Layer의 가중치로 reduction ratio $r$에 의해 복잡도 (파라미터 개수)가 결정됩니다.
SE Block은 기본적으로 GAP를 통해 다차원의 벡터를 단일 스칼라로 압축하게 됩니다. 이는 채널에서 추출했을 지도 모를 작은 객체에 대한 정보를 잃어버릴 수 있는 문제점이 있죠. 이러한 문제를 해결하기 위해 본 논문에서는 Multi-Scale feature context를 활용할 것을 제안합니다.
2) Aggregating Local and Global Contexts

위 그림은 본 논문의 핵심이 되는 MS-CAM의 블록 다이어그램입니다. 이번 절의 제목에서도 볼 수 있다싶이 Local Context와 Global Context를 하나로 합치는 것이 중요한 문제입니다. 이를 위해 본 논문에서는 두 개의 흐름으로 나뉘게 됩니다. 먼저 Local Context를 추출하기 위해 다음과 같이 진행됩니다. 이는 오른쪽 흐름에 해당합니다.
$$\mathbf{L}(\mathbf{X}) = \mathcal{B} (\text{PWConv}_{2} \delta (\mathcal{B} (\text{PWConv}_{1} (\mathbf{X})))) $$
여기서 $ \text{PWConv}_{1} $와 $ \text{PWConv}_{2} $는 Point-wise Convolution으로 $1 \times 1$ Convolution을 의미합니다. 그리고 각 연산은 $\frac{C}{r} \times C \times 1 \times 1$ 그리고 $C \times \frac{C}{r} \times 1 \times 1$의 커널 사이즈로 구성됩니다. 이는 Fully-Connected를 사용하는 SE Block과 동일하게 연산량을 줄이기 위한 reduction ratio $r$이 존재하게 됩니다. Global Context에 해당하는 $\mathbf{G} (\mathbf{X})$ 같은 경우에는 $\mathbf{L}(\mathbf{X})$에서 앞에 GAP를 먼저 통과시켜 channel descriptor를 추출한 뒤 진행하면 됩니다. 다음으로 두 결과를 하나로 종합하여 채널 어텐션 맵을 통해 어텐션을 수행합니다.
$$\mathbf{X}^{'} = \mathbf{X} \otimes \mathbf{M} (\mathbf{X}) = \mathbf{X} \otimes \sigma (\mathbf{L} (\mathbf{X}) \oplus \mathbf{G} (\mathbf{X}) )$$
Attentional Feature Fusion
이전 절에서는 입력 feature map $\mathbf{X}$에 대해 연산하는 과정을 보았지만 여전히 두 개 이상의 feature map을 조합하는 feature fusion이 수행되지는 않았습니다. 이번 절에서는 이 과정이 어떻게 수행되는 지 확인해보도록 하겠습니다.
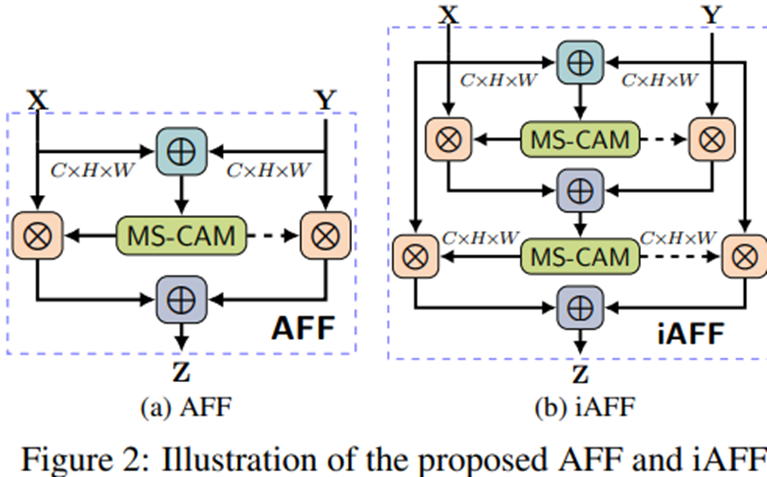
그림 2에서는 AFF와 iAFF를 보여주고 있습니다. 일단, AFF부터 보도록 하죠. 여기서 $\oplus$는 원소별 덧셈을 의미합니다. 즉, 처음에 두 개의 feature map $\mathbf{X}$와 $\mathbf{Y}$를 입력받으면 두 feature map을 더한 뒤 MS-CAM을 적용하는 것을 볼 수 있죠. 아주 간단합니다! 이를 수식으로 정리하면 다음과 같이 쓸 수 있습니다.
$$\mathbf{Z} = \mathbf{M} (\mathbf{X} \uplus \mathbf{Y}) \otimes \mathbf{X} + (1 - \mathbf{M} (\mathbf{X} \uplus \mathbf{Y})) \otimes \mathbf{Y}$$
여기서 $\uplus$는 initial feature integration operation으로 본 논문에서는 단순 합으로 정의하였습니다. iAFF는 AFF를 여러번 더 반복하는 것을 의미합니다. 이 경우에는 $\uplus$를 다음과 같이 정의합니다.
$$\mathbf{X} \uplus \mathbf{Y} = \mathbf{M} (\mathbf{X} + \mathbf{Y}) \otimes \mathbf{Y} + (1 - \mathbf{M} (\mathbf{X}) + \mathbf{Y}) \otimes \mathbf{Y}$$
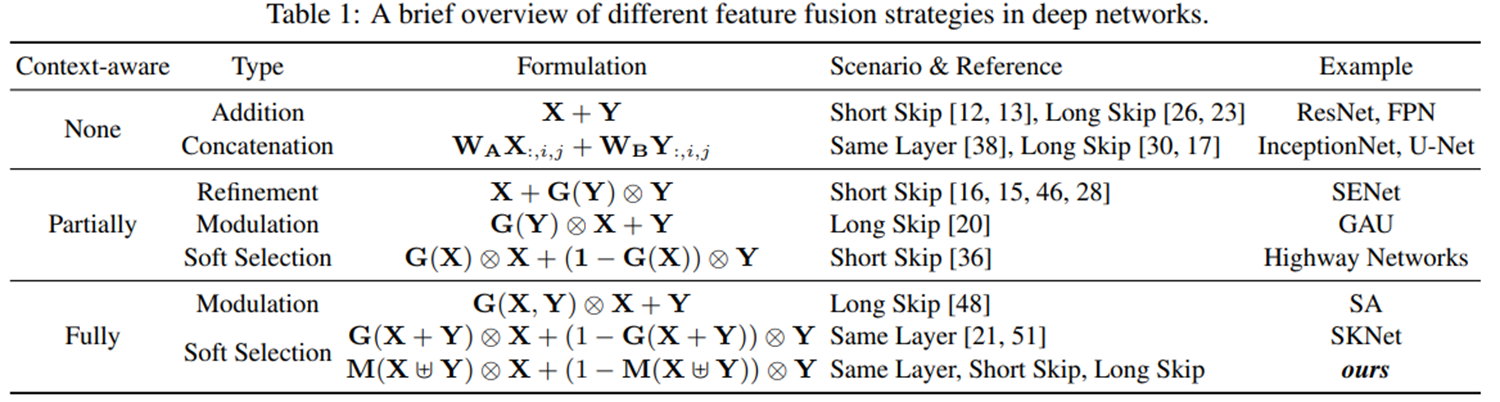
표 1은 지금까지 제안된 다양한 채널 어텐션 모듈들과 본 논문에서 제안된 AFF의 수식적인 차이를 보여주고 있습니다.
Experiment Results
1) Ablation Study


먼저 본 논문에서는 그림 4와 같이 Global + Global 그리고 Local + Local Feature Aggregation 변형 모델을 구현한 뒤 Global + Local Feature Aggregation의 효과에 대해서 보여주고 있습니다. 이는 AFF 모듈을 InceptionNet, ResNet, FPN에 적용한 결과를 표 3에서 볼 수 있습니다. 결과적으로 Global + Local Feature를 사용하는 것이 전체적으로 성능이 좋은 것을 볼 수 있습니다.
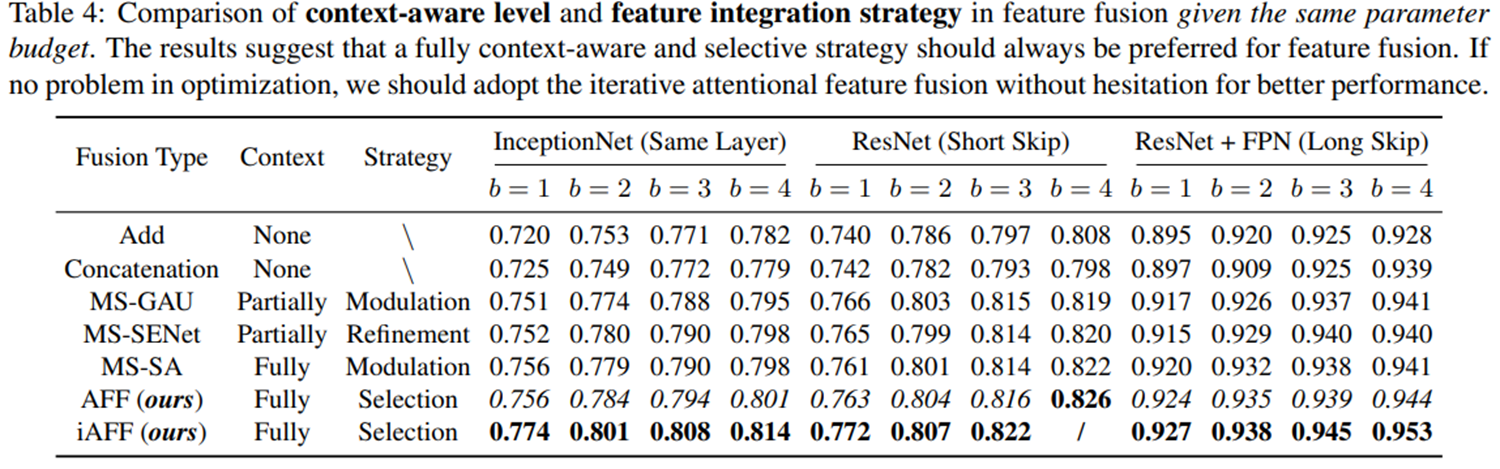

다음으로 그림 5와 같이 표 1에서 보았던 기존 채널 어텐션 모델들인 GAU와 SE Block, SA Block 등의 형태로 실험을 진행하였습니다. 결과적으로 AFF와 iAFF의 형태로 했을 때 가장 좋은 성능을 보이네요.
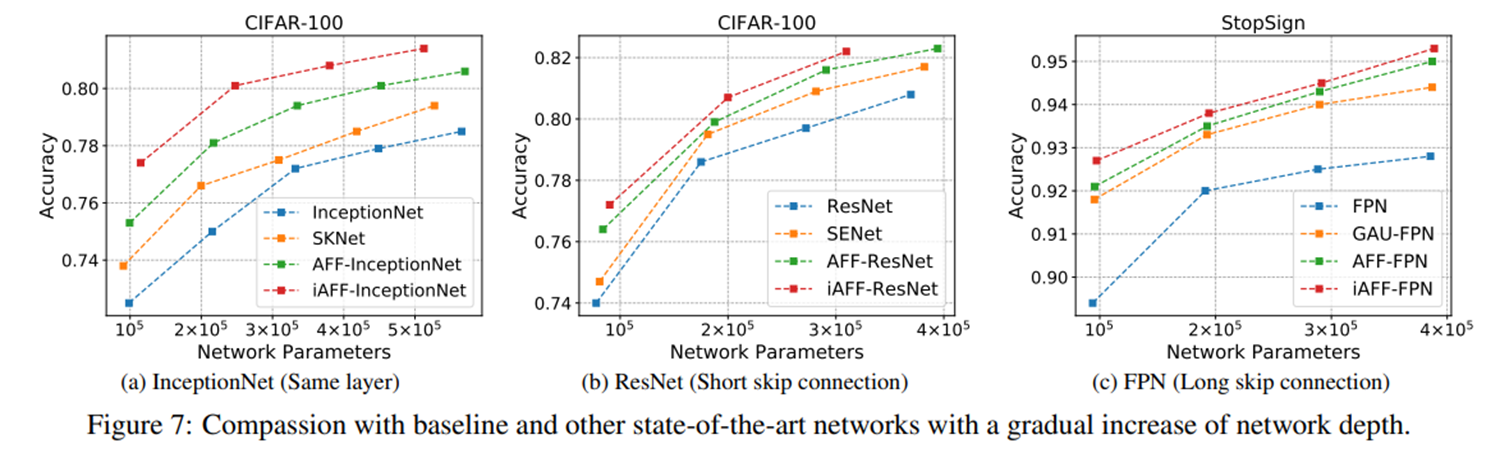
뿐만 아니라 그림 7에서와 같이 전체적으로 efficiency도 잘 보존되는 것을 볼 수 있습니다.
2) ImageNet Classification

'Paper Review' 카테고리의 다른 글
| GhostNet: More Features from Cheap Operations (CVPR2020) (0) | 2024.06.26 |
|---|---|
| Transformer in Transformer (NIPS2021) (0) | 2024.05.20 |
| RefineNet: Multi-Path Refinement Networks for High Resolution Semantic Segmentation (CVPR2017) (0) | 2024.05.04 |
| Pyramid Scene Parsing Network (CVPR2017) (1) | 2024.05.01 |
| CondenseNet V2: Sparse Feature Reactivation for Deep Networks (CVPR2021) (0) | 2024.04.27 |
