안녕하세요 지난 포스팅의 [Transformer] Tokens-to-Token ViT: Training Vision Transformer from Scratch on ImageNet (ICCV2021)에서는 Soft-Split 기반의 Tokenization을 적용한 T2T에 대해서 알아보았습니다. 오늘은 패치뿐만 아니라 패치 내의 서브 패치들간 관계성을 함께 학습하는 TNT에 대해서 소개해드리도록 하겠습니다.
Background
자연어 처리 분야에서 높은 관심을 받고 있던 Transformer를 비전 분야에 최초로 적용한 ViT를 시작으로 수많은 Transformer들이 컴퓨터 비전 분야에 활용되기 시작하였습니다. 이는 기본적으로 입력 영상을 패치들로 나누어 각 패치들간 관계성을 학습하기 때문에 Global Dependency 또는 Long-range Dependency를 학습하는 데 CNN 기반 모델들보다 효율적이라는 사실에 기반하죠. 하지만, 컴퓨터 비전 분야에서 다루는 영상은 자연어와는 다르게 입출력 간 의미론적 차이가 상이하고 동일 패치 내에서도 상이한 정보가 많이 포함된 경우가 많습니다.
본 논문에서는 이러한 문제점을 지적하며 입력 영상의 패치를 한번 더 나누어 서브패치를 구성한 뒤 학습하는 Transformer iN Transformer (TNT)를 제안합니다. 이는 서브패치의 관계성을 패치 내에서 한번 더 이해하고 이에 포함되는 패치로 어텐션을 한번 더 수행하기 때문에 Transformer는 보다 복잡한 형태의 영상에서도 강건한 학습을 진행할 수 있습니다. 뿐만 아니라 TNT에서 수행하는 연산량은 성능향상에 비해 생각보다 적기 때문에 효율성도 달성하였다고 볼 수 있습니다.
Proposed Method
Standard ViT의 전체적인 설명는 이전 포스팅의 ViT (ICLR2021)을 참고해주시길 바랍니다. 핵심 키워드는 Multi-head Self-Attention (MSA), Multi-Layer Perceptron (MLP), Layer Normalization (LN)입니다.
1) Overall Architecture

그림 1은 TNT의 전체적인 구조를 보여주고 있습니다. 사실 전체적인 개념은 굉장히 단순합니다. ViT에서는 패치를 한번 나누고 끝이지만 TNT에서는 나눈 패치를 한번 더 서브패치로 나눈다는 게 핵심이죠. 이를 자연어 처리의 개념과 엮기 위해 패치를 Visual Sentence라고 하고 서브패치를 Visual Word라고 하겠습니다. Sentence안에 Word가 포함되어 있으니 어느정도 합당한 용어 설정인 거 같습니다.
2) Word Level Processing
먼저 Visual Word에서 수행되는 연산과정은 다음과 같습니다.
STEP1. 2D 영상이 주어졌을 때 $(p, p)$ 크기의 해상도를 가지는 $n$개의 패치로 나누어줍니다.
$$\mathcal{X} = [X^{1}, X^{2}, \dots, X^{n}] \in \mathbb{R}^{n \times p \times p \times 3}$$
여기서 $\mathcal{X}$는 Visual Sentence를 의미합니다.
STEP2. 각각의 Visual Sentence $X^{i}$를 다시 한번 $(s, s)$ 크기의 해상도를 가지는 $m$개의 서브패치 $x^{i, j} \in \mathbb{R}^{s \times s \times 3}$로 나누어줍니다.
$$X^{i} = [x^{i, 1}, x^{i, 2}, \dots, x^{i, m}]$$
여기서 $x^{i, j}$는 $i$번째 Visual Sentence $X^{i}$에 포함된 $j$번째 Visual Word에 해당합니다.
STEP3. Visual Word를 임베딩시켜줍니다.
$$y^{i, j} = \text{FC} (\text{Vec} (x^{i, j})) \in \mathbb{R}^{c}$$
여기서 $\text{Vec} (\cdot)$는 Flatten으로 Visual Word를 벡터화 (Vectorization)시켜주는 연산 $\text{FC} (\cdot)$는 Linear Projection을 위한 Fully-Connected Layer를 의미합니다.
STEP4. 임베딩시킨 벡터들의 집합을 $Y^{i} = [y^{i, 1}, y^{i, 2}, \dots, y^{i, m}]$을 Transformer에 $L$번 반복하여 연산을 수행합니다.
$$\begin{cases} &Y^{' i}_{l} = Y^{i}_{l - 1} + \text{MSA} (\text{LN} (Y^{i}_{l - 1})) \\ &Y^{i}_{l} = Y^{' i}_{l} + \text{MLP} (\text{LN} (Y^{' i}_{l})) \end{cases}$$
이와 같이 Transformer 연산을 $l$번째 반복한 Visual Word $\mathcal{Y}_{l} = [Y^{1}_{l}, Y^{2}_{l}, \dots, Y^{m}_{l}]$을 Inner Transformer Block의 출력이라고 볼 수 있습니다.
3) Sentence Level Processing
다음으로 Visual Sentence에서 수행되는 연산과정은 클래스 토큰을 만드는 과정을 포함하여 ViT와 거의 동일합니다. 일단, 입력 영상을 $n$개의 패치로 나누는 과정이 포함되고 거기에 클래스 토큰을 concatentation하여 입력 토큰 $\mathcal{Z}_{0}$를 만들어줍니다. 이때, 클래스 토큰 $Z_{\text{class}}$는 0으로 초기화됩니다.
$$\mathcal{Z}_{0} = [Z_{\text{class}}, Z_{0}^{1}, Z_{0}^{2}, \dots, Z_{0}^{n}] \in \mathbb{R}^{(n + 1) \times d}$$
본격적인 ViT 기반의 Transformer 연산을 진행하기 전에 Word Level Processing 과정에서 얻은 $i$번째 패치의 서브 패치에 대한 연산결과 $Y^{i}_{l}$를 더해줍니다.
$$Z^{i}_{l - 1} = Z^{i}_{l - 1} + \text{FC} (\text{Vec} (Y^{i}_{l})) \in \mathbb{R}^{d}$$
여기서 $d$는 linear projection되는 hidden dimension을 의미합니다. 그리고 다음 단계는 저희가 알고 있는 Transformer Block을 통과시켜주면 됩니다.
$$\begin{cases} &Z^{'}_{l} = Z_{l - 1} + \text{MSA} (\text{LN} (Z_{l - 1})) \\ &Z_{l} = Z^{'}_{l} + \text{MLP} (\text{LN} (Z^{'}_{l})) \end{cases}$$
이렇게 얻은 $\mathcal{Z}_{l} = [Z^{1}_{l}, Z^{2}_{l}, \dots, Z^{n}_{l}]$을 Outer Transformer Block의 출력이라고 볼 수 있습니다. 따라서 최종적으로 TNT의 출력은 $\mathcal{Y}_{l}, \mathcal{Z}_{l} = \text{TNT} (\mathcal{Y}_{l - 1}, \mathcal{Z}_{l - 1})$이 됩니다. 또한, Visual Sentence와 Visual Word level 별로 positional encoding을 따로 해주면 됩니다.
$$\mathcal{Z}_{0} = \mathcal{Z}_{0} + E_{\text{sentence}}$$
$$Y^{i}_{0} = Y^{i}_{0} + E_{\text{word}}$$
여기서 $E_{\text{sentence}} \in \mathbb{R}^{(n + 1) \times d}$이고 $E_{\text{word}} \in \mathbb{R}^{m \times c}$입니다.
4) Network Architecture

Experiment Results
1) Training Settings

2) ImageNet Classification

3) Efficiency Analysis

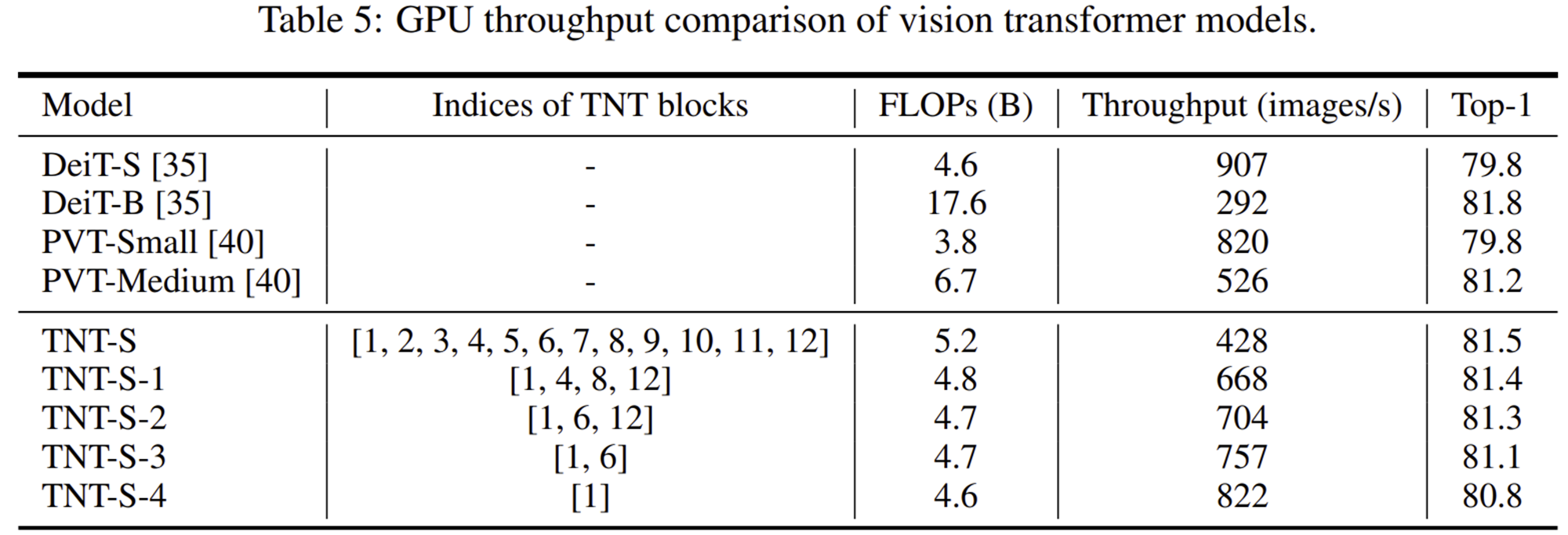
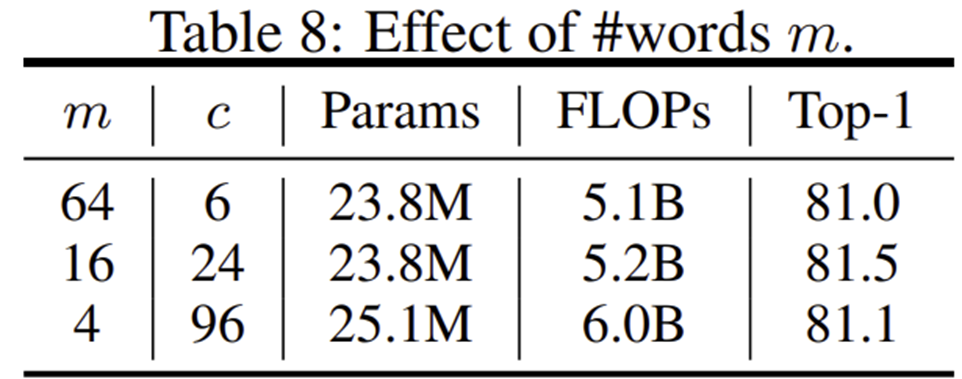
4) Ablation Study


'Paper Review' 카테고리의 다른 글
| Escaping the Big Data Paradigm with Compact Transformers (arxiv2021) (0) | 2024.07.24 |
|---|---|
| GhostNet: More Features from Cheap Operations (CVPR2020) (0) | 2024.06.26 |
| Attention Feature Fusion (WACV2021) (0) | 2024.05.16 |
| RefineNet: Multi-Path Refinement Networks for High Resolution Semantic Segmentation (CVPR2017) (0) | 2024.05.04 |
| Pyramid Scene Parsing Network (CVPR2017) (1) | 2024.05.01 |
