안녕하세요. 지금까지 Transformer가 유명하다는 것은 알았지만 게을러서 공부를 안하고 있다가 최근 연구실에서 Transformer를 공부할 일이 생겨 차근차근 정리를 해보기 위해 트랜스포머 관련 논문을 리뷰하기로 하였습니다. 해당 카테고리에는 영상 분류 (Image Classification) 및 영상 분할 (Image Segmentation)을 Transformer 로 사용한 모든 논문들을 포함시킬 예정입니다. 다만, 이후에 분류를 위해 태그에 영상 분류인 경우 IC2D, 영상 분할인 경우 IS2D와 같이 추가하도록 하겠습니다. 오늘은 Transformer 를 영상 인식을 위해 적용한 가장 유명한 논문인 Vision Transformer에 대해서 소개하도록 하겠습니다. 이전에 Transformer는 다음 포스팅을 보고 오시길 추천드립니다.
16-01 트랜스포머(Transformer)
* 이번 챕터는 앞서 설명한 어텐션 메커니즘 챕터에 대한 사전 이해가 필요합니다. 트랜스포머(Transformer)는 2017년 구글이 발표한 논문인 Attention i…
wikidocs.net
An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale
While the Transformer architecture has become the de-facto standard for natural language processing tasks, its applications to computer vision remain limited. In vision, attention is either applied in conjunction with convolutional networks, or used to rep
arxiv.org
Background
Natural Language Processing (NLP)에서 Transformer 기반의 self-attention은 computational efficiency하고 scalable하기 때문에 대규모 말뭉치 (Corpus) 데이터셋에서 학습한 뒤 소규모 데이터셋으로의 fine-tuning 시 잘 동작한다고 합니다. 하지만, Computer Vision 분야에서는 여전히 Convolutional Neural Network (CNN)가 지배적인 영상 인식 모델로 자리잡고 있습니다. 물론 이전에 Transformer가 NLP에 적용되어 기계 번역 분야에서 큰 성능 향상을 보인 이후 아래 그림과 같이 self-attention 매커니즘을 CNN에 도입 (Non-Local Block)하거나 CNN 및 Transformer의 융합 구조를 적용 (DETR)하는 사례는 존재하였습니다.

하지만, 이러한 방법들은 효율적이지 못하기 때문에 본 논문에서는 오직 Transformer 구조만을 영상 인식 분야에 적용하기 위한 Vision Transformer (ViT)를 제안합니다.
Method
1). Vision Transformer

그림 1은 ViT의 전체적인 구조입니다. 일단, Transformer에 대해서 공부하셨다면 기본적으로 1D sequence 데이터를 입력으로 받아야한다는 것을 알게 되셨을겁니다. 하지만, 영상은 주로 2차원 (Gray) 또는 3차원 (Color) 행렬로 이루어져있기 때문에 이를 적절하게 변형하는 것이 중요하겠죠.
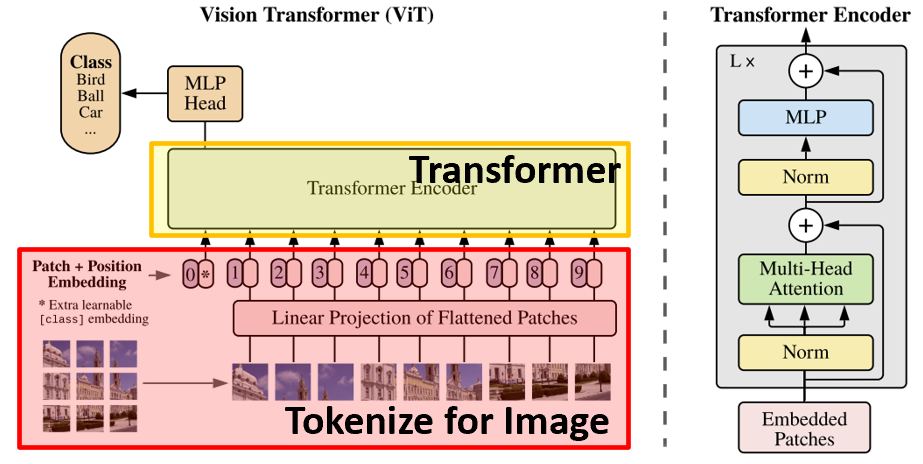
따라서 본 논문에서는 위 그림과 같이 입력 영상을 미리 정의된 패치 크기에 따라 패치로 쪼개줍니다. 이 과정을 Tokenize라고 하겠습니다. 그러면 입력 영상 $\mathbf{x} \in \mathbb{R}^{H \times W \times C}$은 $N$개의 패치로 이루어진 $\mathbf{x} \in \mathbb{R}^{N \times (P^{2} \cdot C)}$로 나누어집니다. 이때, 각 패치는 $(P, P)$ 크기로 구성되고 전체 패치의 개수는 $N = HW / P^{2}$임을 알 수 있죠.
하지만, 여전히 각 패치는 2차원 또는 3차원 행렬로 구성되어 있기 때문에 이를 1차원 벡터로 변형하기 위해 flatten을 적용 한 뒤 linear projection을 통해 hidden dimension $D$로 바꾸어줍니다. 즉, $i$번째 패치 $\mathbf{x}^{i}_{p} \in \mathbb{R}^{P^{2} \cdot C}$에 대해 linear projection $\mathbf{E} \in \mathbb{R}^{(P^{2} \cdot C) \times D}$을 적용하는 것이죠. 그러면 각 패치는 $\mathbf{x}^{i}_{p}\mathbf{E} \in \mathbb{R}^{D}$가 됩니다. 이러한 연산을 전체 패치의 개수 $N$번 만큼 반복하기 때문에 linear projection을 통해 $[\mathbf{x}^{1}_{p}\mathbf{E}, \dots, \mathbf{x}^{N}\mathbf{E}] \in \mathbb{R}^{N \times D}$와 같이 각 임베딩된 패치가 1차원 데이터인 결과를 얻을 수 있습니다. 이때, hidden dimension $D$는 Transformer 내부의 모든 계층에서 동일하게 적용되는 차원의 크기입니다.
저는 Computer Vision을 주로 연구하기 때문에 BERT에 대해 자세히 알지는 못하지만 본 논문에 따르면 BERT와 마찬가지로 첫번째 토큰 $\mathbf{z}_{0}^{0} = \mathbf{x}_{\text{class}}$으로 [class] 정보를 추가해준다고 합니다. 그러면 최종적으로 얻을 수 있는 linear projection 결과는 다음과 같습니다.
$$[\mathbf{x}_{\text{class}}, \mathbf{x}^{1}_{p}\mathbf{E}, \dots, \mathbf{x}^{N}_{p}\mathbf{E}] \in \mathbb{R}^{(N + 1) \times D}$$
여기서 중요한 점은 class 토큰 역시 $D$개의 원소로 이루어진 1D 벡터라는 것이죠. 이 벡터는 이후에 학습과정에서 이미지 전체에 대한 표현을 나타낸다고 합니다. 다음으로 Transformer가 패치 간 위치 정보를 이해하기 위해 positional encoding을 적용해줍니다. 방식은 Transformer와 동일하게 행렬 합으로 인코딩됩니다. 그러면 Transformer에 입력되기 전까지 진행과정은 다음과 같죠.
$$\mathbf{z}_{0} = [\mathbf{x}_{\text{class}}, \mathbf{x}^{1}_{p}\mathbf{E}, \dots, \mathbf{x}^{N}_{p}\mathbf{E}] + \mathbf{E}_{pos}$$
사실 다음 단계부터는 Transformer의 인코딩 과정에 동일하기 때문에 크게 어렵지 않습니다. 전체적인 과정은 Multi-head Self-Attention (MSA)와 Multi-Layer Perceptron (MLP)로 구성되어 연산이 진행됩니다. 이 과정에서 Layer Normalization와 GELU 활성화함수 그리고 residual connection도 함께 적용됩니다. 이와 같은 연산이 총 $L$번 반복되면 $\mathbf{z}_{L}^{0} \in \mathbb{R}^{D}$에는 영상에 대한 잠재 정보가 임베딩 된다고 합니다. 따라서, 해당 벡터를 최종 영상 분류를 위한 MLP head에 통과 시켜 $C$개의 클래스 중 하나로 예측하게 됩니다.
지금까지 말씀드린 과정을 수식으로 나타내면 다음과 같습니다.

2). Inductive Bias
기본적으로 CNN은 커널 기반의 합성곱 연산과 풀링연산을 수행하기 때문에 Locality, 2D Neighborhood Structure, Translation Equivariance와 같은 특성을 가지고 있습니다. 하지만, ViT는 Inductive Bias가 CNN 보다 상대적으로 약한 편 입니다. 이러한 문제를 해결하기 위해 data-driven training을 통해 데이터의 양으로 밀어붙여 이러한 문제를 해결하고자 합니다.
3). Hybrid Architecture
기본적으로 입력 영상 자체로부터 패치로 나누어 진행할 수도있지만 CNN의 출력 특징 맵을 추출된 패치로 보고 CNN + Transformer의 융합 구조도 적용해볼 수 있습니다.
4). Transformer Model Variants
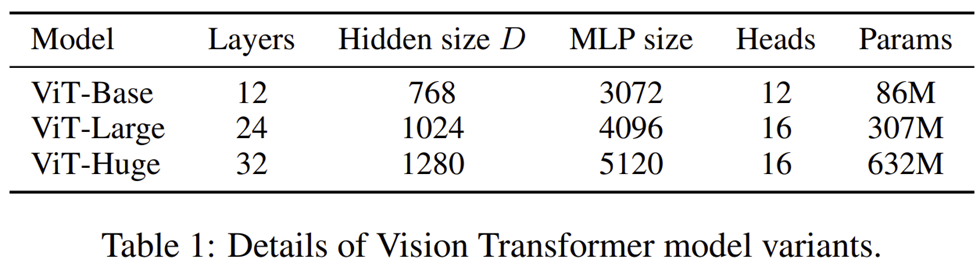
ViT는 사용하는 Transformer의 개수 (Layers), hidden dimension $D$, MLP의 개수, Head의 개수에 따라 Base, Large, Huge로 나눌 수 있습니다. 모델 구조에 따라 파라미터의 개수는 86M부터 632M까지 차이가 나는 것을 볼 수 있습니다.
Experiment Results
1). Experiment Settings

표3은 ViT과 ResNet의 학습 세팅을 보여주고 있습니다.
2). ImageNet Classification Results
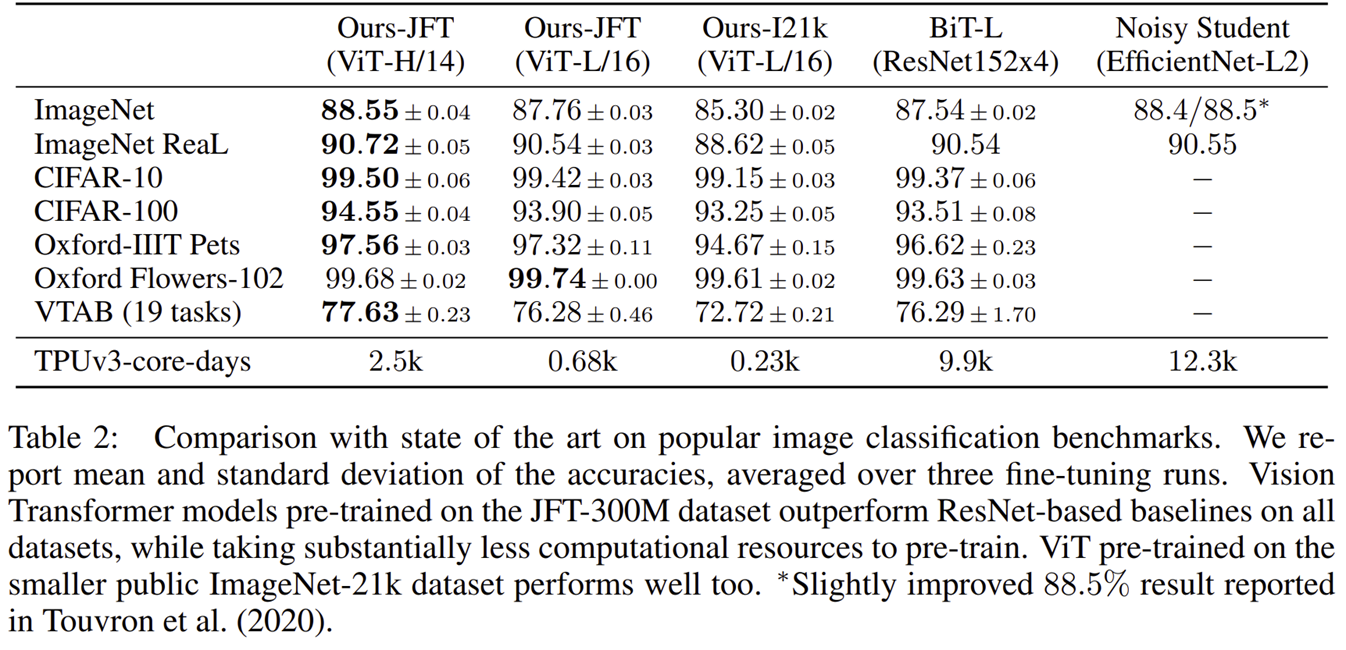
실험 결과는 기존의 CNN 구조의 ResNet-152보다 높은 성능을 보이고 있습니다.
