안녕하세요. 지난 포스팅의 [IC2D] Searching for MobileNetV3 (ICCV2019)에서는 MobileNetV2와 MNAS + NetAdapt 알고리즘을 결합하여 좀 더 효율적인 모델인 MobileNetV3를 제안하였습니다. 오늘은 새로운 합성곱 연산인 OctConv에 대해서 소개하고자 합니다.
Drop an Octave: Reducing Spatial Redundancy in Convolutional Neural Networks with Octave Convolution
In natural images, information is conveyed at different frequencies where higher frequencies are usually encoded with fine details and lower frequencies are usually encoded with global structures. Similarly, the output feature maps of a convolution layer c
arxiv.org
Background
심층 신경망을 효율적으로 구성하기 위해서는 CNN으로부터 추출한 특징 맵의 중복되는 쓸모없는 특징 맵들을 줄이는 것이 중요합니다. 이를 위해 크게 2가지 방식으로 나누어 연구가 진행되었습니다. 첫번째 전략은 모델의 파라미터를 조밀하게 연결하지 않고 sparse하게 구성하여 중복 특징 맵들이 삭제되기를 바랍니다. 대표적으로 DSD, ThiNet, Clip-Q 등과 같은 논문들이 이러한 방식을 채택하고 있다고 합니다. 아직 저는 해당 논문들을 안읽어봐서 해당 접근방식은 잘 이해하고 있지 않습니다. 두번째 전략은 추출된 특징 맵의 채널의 차원을 줄이는 것 입니다. 대표적으로 ResNext, MobileNet, XCeptionNet이 있었죠. 저희는 주로 두번째 전략에 대해서 많이 이야기를 해왔습니다.
하지만, 이러한 모델들이 간과하고 있는 것이 한가지 있습니다. 특징 맵의 채널 간에 중복되는 정보가 존재할 수 있다면 같은 공간을 기준으로도 중복되는 정보들이 존재할 수도 있지 않을까요? 본 논문에서는 이러한 점을 지적하였습니다.

위 그림을 한번 봐주시길 바랍니다. 일반적으로 신호에서 저주파 및 고주파 신호를 나누듯이 영상에서도 위와 같이 나누어서 생각해볼 수 있습니다. 이때, 저주파 영상은 주로 주변 픽셀값 사이의 차이가 크게 나지 않은 smooth한 영역을 의미합니다. 반대로 고주파 영상은 차이가 큰 sharp한 영역을 의미하죠. 그래서 위 그림과 같이 고주파 영상은 주로 객체의 가장자리 영역을 얻게 됩니다. 이때, 중복되는 특징을 많이 가지는 부분은 어디일까요? 아무래도 저주파 영역이 고주파 영역보다 유사한 정보들이 더 많이 모여있을 것 으로 예상됩니다. 따라서, 본 논문에서 제안하는 새로운 합성곱 연산은 2개의 단계로 나눌 수 있습니다. 1). 저주파 및 고주파로 분해한 뒤 2). 각 저주파 및 고주파 영상에 대한 합성곱 연산을 수행하는 것이죠.
Method
1). Octave Feature Representation
일단 Vanilla 합성곱 연산은 커널의 크기가 3일 때 stride = 1, padding = 1로 잡으면 입력 및 출력 특징 맵의 해상도가 동일하게 됩니다. 이러한 합성곱 연산의 특징은 공간을 기준으로 픽셀에 대한 중복되는 특징이 생길 가능성이 높다는 것을 의미합니다. 이러한 문제를 해결하기 위해 본 논문에서 새로운 특징인 Octave Feature Representation을 제안합니다. 이 특징은 기본적으로 Background에서도 설명드렸다싶이 저주파 및 고주파로 분해되어있습니다. 혹시, 웨이블릿 변환 (Wavelet Transform)에 대해서 들으셨을 지 모르겠습니다. 본 논문에서는 웨이블릿 변환의 기본 이론 중 하나인 Scale-Space Theorem을 활용하여 저주파와 고주파 특징 사이의 옥타브 (octave)가 하나를 차이나게 구성합니다. 이때, 옥타브는 두 특징 맵의 차이가 가로 및 세로로 절반씩 줄어들었다는 것을 의미합니다. 원래 웨이블릿 변환에서는 총 n번의 변환을 하여 최종적으로 $2^{n}$배만큼 감소한 해상도를 가지는 저주파 이미지를 얻을 수 있지만 본 논문에서는 $n = 1$일 경우에 집중합니다.
지금까지는 해상도, 즉 공간에 대한 기준을 설명했습니다. 하지만 저희는 총 $c$개의 채널을 가지는 특징 맵 $X \in \mathbb{R}^{c \times h \times w}$에 대해서 다루어야합니다. 이를 위해 본 논문에서는 하이퍼파라미터로 $\alpha \in [0, 1]$를 도입합니다. $\alpha$는 $c$개의 채널 중 얼마나 저주파 특징으로 삼을 것인지에 대한 비율을 의미합니다. 따라서, 저주파 및 고주파 특징 맵의 크기는 각각 $X^{L} \in \mathbb{R}^{\alpha c \times \frac{h}{2} \times \frac{w}{2}}$와 $X^{H} \in \mathbb{R}^{(1 - \alpha)c \times h \times w}$가 됩니다. 저주파 특징 맵의 크기가 고주파에 비해 절반인 이유는 이전 문단에서 설명했으니 넘어가도록 하겠습니다. 저희가 지금까지 한 것은 입력 특징 맵 $X$를 두 개의 주파수로 분해하는 과정에 대해서 설명하였습니다.
2). Octave Convolution
저희는 현재 분해된 두 입력 특징 맵인 $X = \{ X^{H}, X^{L} \}$을 통해 두 출력 특징 맵 $Y = \{ Y^{H}, Y^{L} \}$을 구해야합니다. 물론 가장 단순한 방법은 $X^{H}$만 합성곱 연산을 통해 $Y^{H}$를 구하고 $X^{L}$만 합성곱 연산을 통해 $Y^{L}$을 구하는 방식으로 할 수 있습니다. 하지만, 이렇게 되면 각 주파수 간의 중요한 정보가 소실될 수 있기 때문에 본 논문에서는 서로 다른 주파수 간의 정보 교환을 수행할 수 있도록 하기 위한 Octave Convolution을 제안하는 것이죠. 이것은 본 논문의 핵심입니다. 이를 수식으로 나타내면 다음과 같이 쓸 수 있습니다.
$$\begin{align*} \begin{cases} Y^{H} &= Y^{H \rightarrow H} + Y^{L \rightarrow H} \\ Y^{L} &= Y^{L \rightarrow L} + Y^{H \rightarrow L} \end{cases} \end{align*}$$
이때, 윗첨자에서 같은 문자로 표시되어 있는 것은 intra-frequency update 그리고 다른 문자로 표시되어 있는 것은 inter-frequency communication이라고 언급하고 있습니다. 따라서, 저희는 총 4개의 출력 특징 맵 $Y^{H \rightarrow H}, Y^{H \rightarrow L}, Y^{L \rightarrow H}, Y^{L \rightarrow L}$을 얻어야합니다. 이를 위해 합성곱 필터 $W$ 역시 $\{ W^{H \rightarrow H}, W^{L \rightarrow H}, W^{H \rightarrow L}, W^{L \rightarrow L} \}$과 같이 4개로 나누어줍니다. 그러면 각 필터는 저희가 얻고 싶은 4개의 출력 특징 맵을 얻게 되는 것이죠.
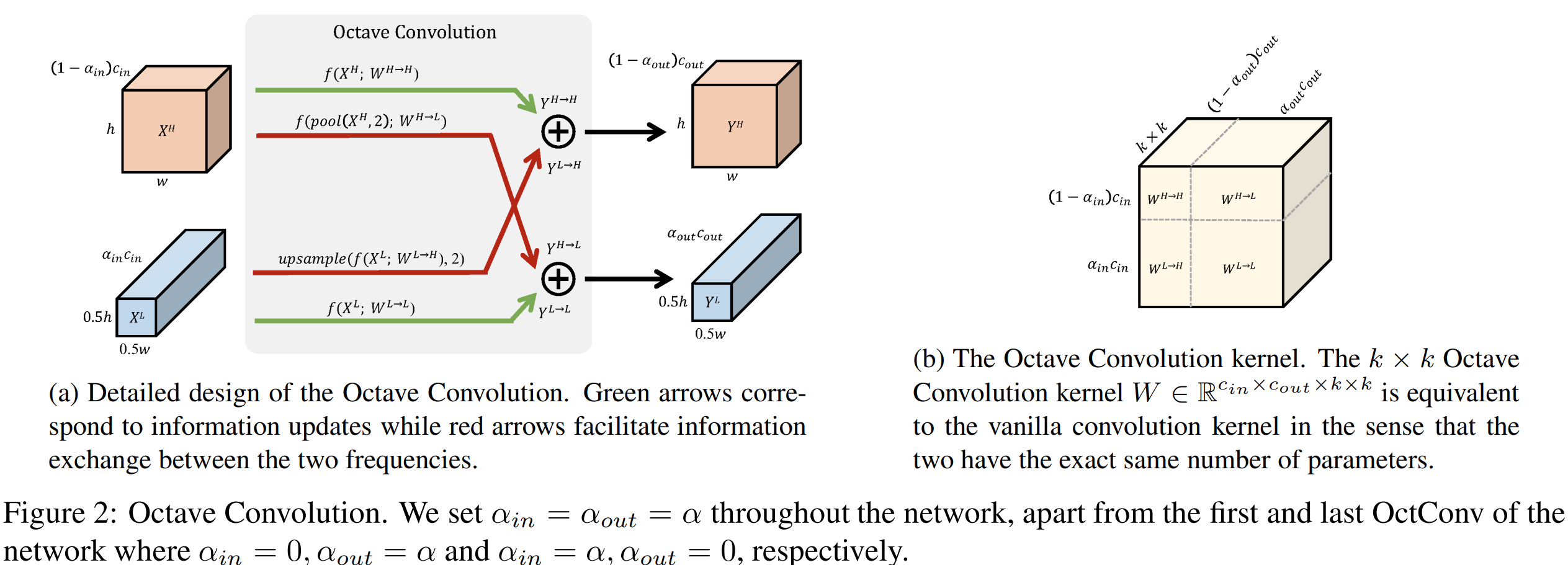
그림2는 이 과정을 전체적으로 요약하고 있습니다. 왼쪽 그림부터 보시면 $Y^{H}$를 얻기 위해 $X^{H}$에서 필터 $W^{H \rightarrow H}$를 통해 합성곱을 수행한 결과와 $X^{L}$에서 필터 $W^{L \rightarrow H}$를 통해 합성곱을 수행한 뒤 해상도가 절반 정도 차이나기 때문에 2배 업샘플링을 한 뒤 더해주는 것을 볼 수 있습니다. 그와는 반대로 $Y^{L}$를 얻기 위해 $X^{L}$에서 필터 $W^{L \rightarrow L}$를 통해 합성곱을 수행한 결과와 $X^{H}$를 먼저 절반으로 줄인 뒤 필터 $W^{H \rightarrow L}$를 통해 합성곱을 수행한 뒤 더해주는 것을 볼 수 있습니다.


위 수식은 지금까지 말씀드린 과정을 수식으로 정리한 것 입니다. 방정식 (3)에서 한 가지 문제점이 있습니다. 바로 인덱스인 $\{ (2 * p + 0.5 + i), (2 * q + 0.5 + j) \}$가 정수가 아니라는 점이죠. 본 논문에서는 stride = 2로 하여 이를 정수 인덱스로 근사시킬 수도 있다고 하였으나 이 경우 misalignment 문제가 발생하여 성능이 하락되었다고 합니다. 따라서, 합성곱을 수행하기 전에 평균 풀링을 적용하는 것이죠.
이러한 OctConv의 장점 중 하나는 Group Convolution이나 Depth-wise Convolution와 동일하게 다른 CNN 기반 모델에 쉽게 적용할 수 있는 점입니다.

표1은 OctConv의 하이퍼파라미터인 $\alpha$에 따른 연산 비용에 대해서 말하고 있습니다. $\alpha$는 결국 저주파 영역을 얼마나 사용할 것인지에 대한 파라미터였습니다. 그리고 저희는 절반으로 4개의 합성곱 연산 중 2개는 절반만큼 줄어든 해상도에 대해서 합성곱 연산을 적용하기 때문에 당연히 $\alpha$가 커질수록 연산량이 줄어들 것이라는 것을 알 수 있습니다.
Experiment Results
1). Ablation Study on ImageNet

본 논문에서는 먼저 OctConv를 다양한 CNN 기반 모델에 적용하여 $\alpha \in \{ 0.125, 0.25, 0.5, 0.75 \}$에 따른 FLOPs vs Accuracy 그래프를 보여주고 있습니다. 눈에 띄는 특징 중에 하나는 모든 CNN 모델에 대해서 오목한 그래프를 보여주고 있습니다. 또한, $\alpha = 0.125$로 했을 때 가장 높은 성능을 얻을 수 있습니다. 하지만, $\alpha = 0.5$로 하게 되면 FLOPs는 거의 절반으로 줄어들지만 성능은 거의 차이가 없거나 더 높은 것을 볼 수가 있죠. 이러한 결과는 실제로 OctConv가 효율적으로 공간 중복 특징을 제거했다는 것을 의미합니다.

또한, 그림4와 같이 분해된 두 특징 맵의 출력의 주파수에 대한 분석을 해보았을 때 고주파 영역에는 주로 고주파가, 저주파 영역에는 주로 저주파로 잘 분해되어 있는 것을 볼 수 있습니다.
2). ImageNet Classification Results


'Paper Review' 카테고리의 다른 글
| An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale (ICLR2021) (2) | 2023.10.01 |
|---|---|
| Selective Kernel Networks (CVPR2019) (0) | 2023.09.28 |
| Searching for MobileNetV3 (ICCV2019) (0) | 2023.09.11 |
| Semantic Image Segmentation with Deep Convolutional Nets and Fully Connected CRFs (ICLR2015) (0) | 2023.09.08 |
| Progressive Neural Architecture Search (ECCV2018) (0) | 2023.09.05 |
