안녕하세요. 지난 포스팅의 [IC2D] Gather-Excite: Exploiting Feature Context in Convolutional Neural Networks (NIPS2018)에서는 Gather-Excite Block이라는 어텐션 모듈에 대해 소개하였습니다. 기본적인 컨셉은 SE Block의 일반화를 목표로하는 것이였습니다. 오늘 알아볼 ECA Block은 이러한 SE Block을 보다 효율적으로 구성하는 방법에 대해서 알려주고 있습니다.
Background
지금까지 저희는 다양한 어텐션 모듈을 보았습니다. 가장 대표적으로 SE Block (CVPR2018)은 입력 특징 맵으로부터 channel descriptor를 얻는 Squeeze 연산과 두 개의 Fully-Connected (FC) Layer로 구성된 서브 모듈에서 가중치를 추출하는 Excite 연산으로 구성되어 있었습니다. 뿐만 아니라 Residual Attention Network (RAN, CVPR2018), Bottleneck Attention Module (BAM, BMVC2018), Convolutional Block Attention Module (CBAM, ECCV2018), Gather-Excite Block (GE Block, NIPS2018)에 대해서도 소개하였습니다. 하지만 이러한 어텐션 모듈들은 점점 더 복잡해져 실용적이지 않다는 문제점이 존재합니다.
따라서, 본 논문의 저자들은 다음과 같은 질문을 던집니다.
Can one learn effective channel attention in a more efficient way?
즉, channel attention 관점에서 어텐션 모듈을 좀 더 효율적으로 바꿀 수 있는 방식에 대해서 생각해보고 있습니다. 이를 위해 본 논문에서는 SE Block의 각 핵심 연산의 필요성을 재검토합니다. 다음으로 필요없는 연산을 제거하여 최종적으로 Efficient Channel Attention (ECA) Block을 제안하게 되는 것이죠. 본 논문의 기여를 정리하면 다음과 같습니다.
- CNN을 위한 ECA Block 제안
- Dimensionality reduction 과정 제거
- 효율적으로 인접 채널 간 상호작용 고려
- Channel attention을 위한 영역을 적응적으로 결정 가능
Revisiting Channel Attention in SE Block
먼저 기존의 SE Block을 분석해보도록 하겠습니다. $\mathcal{X} \in \mathbb{R}^{W\ times H \times C}$를 이전 합성곱 계층으로부터의 출력 특징 맵이라고 하겠습니다. 여기서 $W, H, C$는 각각 특징 맵의 너비, 높이 그리고 채널의 개수를 의미합니다. 일반적으로 저희는 SE Block의 채널 어텐션 맵을 다음과 같이 추출할 수 있습니다.
$$\omega = \sigma (f_{\{ \mathbf{W}_{1}, \mathbf{W}_{2} \}} (g (\mathcal{X}))) - (1)$$
여기서 $g( \cdot )$는 channel descriptor를 추출하는 연산으로 SE Block 기준으로 Global Average Pooling에 해당되어 $g(\mathcal{X}) = \frac{1}{HW} \sum_{i = 1, j = 1}^{H, W} \mathcal{X}_{ij}$로 정의됩니다. 그리고 $\sigma (\cdot)$는 sigmoid 함수를 의미하죠. 마지막으로 $f_{\mathbf{W}_{1}, \mathbf{W}_{2}} ( \cdot )$은 excitation 연산을 수행할 수 있는 서브 모듈이라고 하겠습니다. 그러면 SE Block 기준으로 가중치 $\mathbf{W}_{1}$과 $\mathbf{W}_{2}$를 가지는 두 개의 FC layer라고 할 수 있겠습니다. 식을 단순하게 만들기 위해 $\mathbf{y} = g (\mathbf{X})$라고 하죠. 그러면 저희는 기존의 식 (1)을 다음과 같이 바꿀 수 있습니다.
$$\omega = \sigma (f_{\{ \mathbf{W}_{1}, \mathbf{W}_{2} \}} ( \mathbf{y} )) - (2)$$
한편 SE Block에서는 효율적은 excitation 연산을 수행하기 위해 FC 계층의 가중치 형상을 reduction ratio $r$만큼 줄여 연산을 수행합니다. 따라서, $\mathbf{W}_{1} \in \mathbb{R}^{C \times \frac{C}{r}}$ 그리고 $\mathbf{W}_{2} \in \mathbb{R}^{\frac{C}{r} \times C}$와 같은 형상이 되죠. 이는 모델의 복잡도를 줄여주는 데 놀라운 효과를 보이고 실제로 현재 다양한 곳에서 사용되는 테크닉입니다. 하지만 이는 기존의 특징 맵이 가지고 있던 채널의 특성을 붕괴시키기 때문에 실제로 채널 어텐션을 수행 시 채널-가중치 간 정보 불일치가 발생한다는 문제점이 있죠.
Efficient Channel Attention Module
1) Overall Architecture
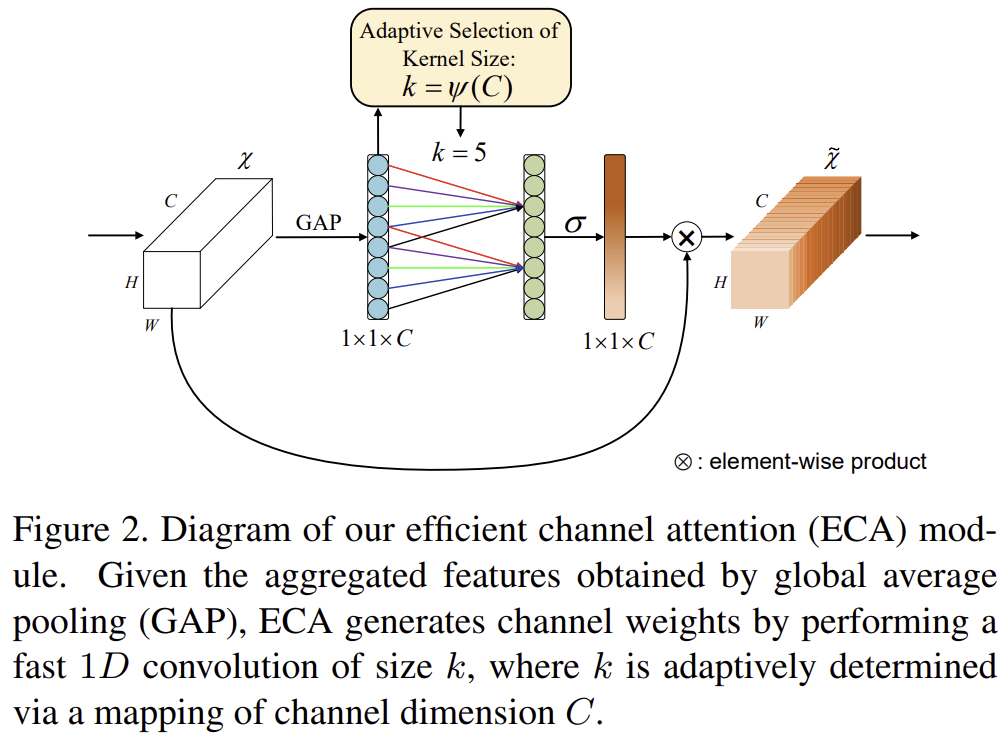
그림 2는 ECA Block의 전체적인 구조를 보여주고 있습니다.

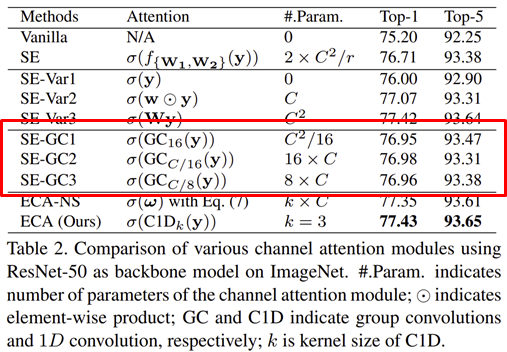
표 1은 기존 어텐션 모듈들간 비교를 Dimensionality Reduction의 유무, Channel 간 상호작용, Efficiency 강조 유무 등을 이용해서 비교하고 있습니다.
2) Avoiding Dimensionality Reduction
먼저, 본 논문의 저자들은 SE Block를 좀 더 깊게 이해하기 위해 3개의 변형 구조를 만들어 ImageNet에 실험해보았습니다.
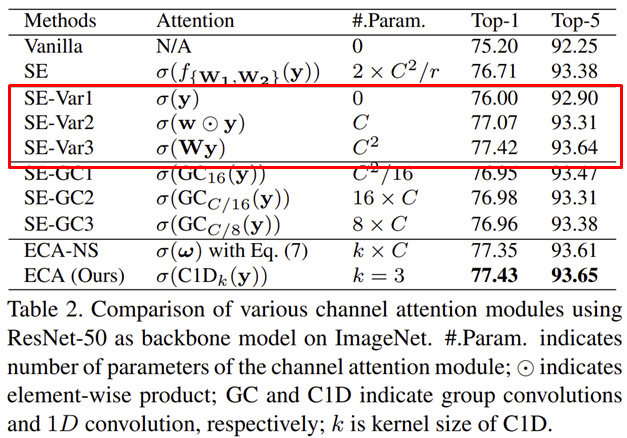
각 모델의 구조는 다음과 같이 설명됩니다.
- SE-Var1: $\sigma (\mathbf{y})$로 파라미터 없이 GAP를 이용하여 channel descriptor를 추출한 뒤 곧바로 Attention 수행
- SE-Var2: $\sigma (\mathbf{w} \odot \mathbf{y})$로 파라미터 $\mathbf{w}$를 벡터로 정의하여 채널간 상호작용은 고려하지 않고 어텐션으로 수행하는 방식. 입력 특징 맵의 채널의 개수가 $C$개라고 할 때 원소별 곱을 위해 파라미터의 개수도 $C$개가 되어야합니다.
- SE-Var3: $\sigma (\mathbf{W}\mathbf{y})$로 파라미터 $\mathbf{W}$를 행렬로 정의하여 모든 채널간 상호작용을 고려하여 어텐션을 수행하는 방식. 모든 채널을 고려한 행렬 연산을 위해 총 $C^{2}$의 파라미터가 필요합니다.
각 변형 구조의 실험 결과를 분석해보면 SE-Var1은 파라미터 기반 모델이 아닌 자기만의 채널 정보를 이용하여 어텐션 했음에도 불구하고 기존 Vanilla보다 0.80%의 성능 향상을 보여주고 있습니다. 이는 실제로 channel attention 자체가 CNN의 성능 향상에 있어 도움을 준다는 것을 의미하죠. 다음으로 SE-Var2의 경우에는 기존의 SE Block보다 적은 파라미터 개수에도 불구하고 0.36%의 아주 약간의 성능 향상을 보여주고 있습니다. 마지막으로 SE-Var3의 경우 단일 FC Layer를 사용하였기 때문에 dimensionality reduction이 없는 상태입니다. 이로 인해 채널-가중치가 정보가 일치할 수 있는 상태가 만들어지기 때문에 기존 SE Block보다 0.71% 더 향상된 성능을 보여주고 있습니다. 이와 같은 결과를 통해 dimensionality reduction의 제거 필요성을 보다 강하게 뒷받침하게 됩니다.
3) Local Cross-Channel Interaction
이제 이전 실험을 통해 dimensionality reduction을 없애야한다는 점을 알았습니다. 그런데 이전 실험에서 SE-Var2와 SE-Var3를 잘 보면 다음으로 하나의 수식으로 통합하여 써볼 수 있습니다.
$$\omega = \sigma (\mathbf{W} \mathbf{y})$$
여기서 $\mathbf{W}$는 아래와 같이 정의할 수 있습니다.
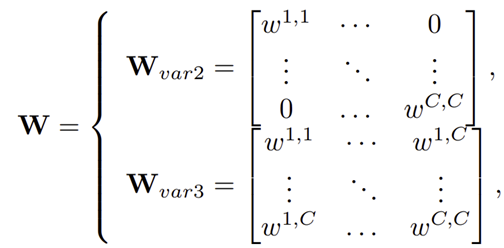
즉, SE-Var2에 해당하는 $\mathbf{W}_{var2}$는 diagonal matrix로 정의되어 채널간 상호작용은 고려하지 않게 되는 것이죠. 다음으로 SE-Var3에 해당하는 $\mathbf{W}_{var3}$는 full matrix로 정의되어 모든 채널간 상호작용을 고려하게 됩니다. 이로 인해 이전 실험에서도 보셨다싶이 모든 채널간 상호작용을 고려하는 SE-Var3가 SE-Var2보다 높은 성능을 얻게 되는 것이라고 볼 수 있습니다. 하지만, SE-Var3는 $C^{2}$개의 파라미터가 필요하기 때문에 이 부분이 문제입니다.
한 가지 대안으로는 다음과 같이 Group Convolution의 형태로 만들어볼 수도 있습니다.
$$\mathbf{W}_{G} = \begin{bmatrix} \mathbf{W}^{1}_{G} & \cdots & \mathbf{0} \\ \vdots & \ddots & \vdots \\ \mathbf{0} & \cdots & W^{G}_{G} \end{bmatrix}$$
위와 같은 방법은 채널을 그룹단위로 묶어 동일한 파라미터로 학습될 수 있도록 하기 때문에 어느정도 효율성을 보장될 수 있습니다. 하지만, 여전히 그룹 간 상호작용을 하지 못하기 때문에 성능이 떨어질 수 밖에 없습니다.
위 실험들과 같이 결국 핵심은 채널 또는 그룹들 간 상호작용을 하는 것이 중요하다는 것입니다. 이를 만족하기 위해서 본 논문에서는 아래와 같은 Band Matrix $\mathbf{W}_{k}$를 사용할 것을 제안합니다.

이는 현재 채널 $c$를 중심으로 주변 $k$개의 채널을 고려하여 SE-Var2와 SE-Var3의 절충안이라고 볼 수 있습니다. 이를 수식으로 표현하면 다음과 같죠. 저희는 이를 ECA-NS (Non-Sharing)이라고 부르겠습니다.
$$\omega_{i} = \sigma \left( \sum_{j = 1}^{k} w_{i}^{j} y_{i}^{j} \right)$$
여기서 $y_{i}^{j} \in \omega_{i}^{j}$로 어텐션되는 영역의 범위를 의미합니다. 그런데 저희는 이 수식에서 한 번더 모든 채널들이 동일한 파라미터를 가진다고 가정해버리면 다음과 같이 쓸 수 있습니다.
$$\omega_{i} = \sigma \left( \sum_{j = 1}^{k} w^{j} y_{i}^{j} \right) = \sigma (\text{C1D}_{k} (\mathbf{y}))$$
결국 저희는 2개의 FC Layer를 가지고 연산해야했던 결과를 1개의 1D Convolution 연산만으로도 충분히 가능하다는 것을 볼 수 있습니다. 그리고 파라미터의 개수는 $k$와 채널의 개수인 $C$에 의존하여 $C^{2}$보다는 작게 됩니다.
4) Coverage of Local Cross-Channel Interaction
하지만, 한가지 문제점이 있습니다. $k$는 현재 $c$번째 채널 기준으로 몇 번째 채널까지로 고려하여 어텐션 맵을 추출할 지에 대한 파라미터입니다. $k = 3$이라고 가정하면 과연 $C = 1028$일 때 3개의 채널을 고려하는 것과 $C = 128$일 때 3개의 채널을 고려하는 것은 똑같을까요? 이러한 문제를 해결하기 위해 본 논문에서는 채널의 개수 $C$에 대해 적응적으로 $k$를 바꿀 수 있는 방법도 함께 제시해줍니다. 이를 위해 $C = \phi (k)$를 정의해두도록 하겠습니다. 이는 현재 채널의 개수와 $k$ 사이의 비율로도 해석할 수 있습니다.
가장 간단하게 $k$의 개수를 바꿀 수 있는 방법은 채널의 개수에 따라 다음과 같이 선형적으로 바꾸는 것일 겁니다.
$$C = \phi (k) = \gamma k - b$$
하지만 이와 같은 방식은 일반적으로 급수의 형태로 채널의 개수가 증가하는 CNN의 특성 상 맞지않습니다. 따라서, 이를 해결하기 위해 다음과 같이 비선형성을 도입합니다.
$$C = \phi (k) = 2^{\gamma k - b}$$
이제 이를 $k$에 대한 식으로 바꾸면 다음과 같은 식을 얻을 수 있습니다.
$$k = \psi (C) = \left| \frac{\log_{2} (C)}{\gamma} + \frac{b}{\gamma} \right|_{odd}$$
여기서 $|t|_{odd}$는 현재 $t$를 기준으로 할 때 가장 가까운 홀수 숫자를 선택한다는 것을 의미합니다. 본 논문에서는 $\gamma = 2$ 그리고 $b = 1$로 설정하였습니다.
5) ECA Module for Deep CNNs

그림 3은 ECA Block을 CNN에 적용하기 위한 Pytorch 코드를 보여주고 있습니다.
Models and Experiments
- Dataset
- ImageNet-1K: 1.28 million training images & 50K validation images with 1,000 classes
- Data Augmentation
- Optimization: Stochastic Gradient Descent
- momentum: 0.9
- weight decay
- ResNet50, ResNet101, ResNet512: 0.0001
- MobileNetV2: 0.00004
- learing rate:
- ResNet50, ResNet101, ResNet512: initial learning rate is set to 0.1 and is reduced by a factor of 10 for every 30 epoch
- MobileNetV2: initial learning rate is set to 0.045 and is linearly reduced by a factor of 0.98
- initial learning rate is set to 0.1 and is reduced by a factor of 10 each time the loss plateaus
- batch size
- ResNet50, ResNet101, ResNet512: 256
- MobileNetV2: 96
- epochs
- ResNet50, ResNet101, ResNet512: 100
- MobileNetV2: 400
- GPU 타입 명시 X