[IC2D] MNASNet: Platform-Aware Neural Architecture Search for Mobile (CVPR2019)

안녕하세요. 지난 포스팅의 [IC2D] EfficientNetV2: Smaller Models and Faster Training (ICML2021)에서는 EfficientNetV1을 좀 더 깊게 분석하고 모델의 경량화를 발전시키기 위한 몇 가지 테크닉이 적용된 EfficientNetV2에 대해서 알아보았습니다. 이때, EfficientNetV2의 baseline 모델을 찾기 위해 EfficientNetV1-B4에서 MNASNet을 적용한 것을 볼 수 있었습니다. 오늘은 MNASNet에 대한 간단한 설명을 진행하도록 하겠습니다. 

 

MnasNet: Platform-Aware Neural Architecture Search for Mobile

 

Background

기본적으로 심층 신경망 모델들은 영상 인식 분야에서 엄청난 성공을 거두게 되었습니다. 이를 위한 밑바탕으로는 보다 큰 규모의 모델을 큰 규모의 데이터셋 (ImageNet) 학습하는 것입니다. 하지만, 모델의 규모가 커질수록 그만큼 모델의 복잡도가 증가하는 것은 당연합니다. 이러한 문제는 최근 제안되고 있는 강력한 성능을 가지는 심층 신경망 모델들을 모바일 및 작은 칩과 같은 자원이 극도로 제한된 플랫폼에서는 사용하기 어렵게 만듭니다. 

 

이와 같이 효율적인 심층 신경망 모델을 만들기 위해 알려진 유명한 모델이 바로 Depth-wise Separable Convolution을 제안한 MobileNetV1이 있습니다. 그리고 Group Convolution 시 channel shuffling을 통해 채널 간 상관성을 향상시킨 ShuffleNetV1도 있었죠. 또한, Automated Neural Architecture Search (NAS) 역시 관련 분야에서 큰 두각을 나타내었습니다. 기존의 MobileNetV1이나 ShuffleNetV1의 경우에는 일일히 최적화된 모델을 수동으로 찾아야 하지만 NAS에서는 이 과정을 자동화하여 자원이 한정된 플랫폼이 주어졌을 때 성능을 최적화할 수 있는 모델을 찾을 수 있죠. 대표적으로 NASNet과 PNASNet이 있었습니다. 하지만, 기존 NAS 기반 모델들의 큰 문제점은 타겟 플랫폼에 대한 inference latency를 FLOPs를 이용하여 간접적으로 구한다는 것 입니다. 이는 실제로 MobileNetV1과 NASNet의 FLOPs는 각각 575M과 564M으로 어느 정도 유사하나 실제 latenecy는 113ms와 183ms로 매우 큰 차이를 보여주고 있습니다. 본 논문에서는 이러한 문제점을 지적하여 실제 inference latency를 직접적으로 구하기 위해 모바일 디바이스를 NAS 과정에 추가하여 최적화를 수행합니다. 

 

본 논문의 핵심 기여는 다음과 같이 정리할 수 있습니다. 

 

- Multi-objective optimization 문제를 수식적으로 정의하여 성능과 직접적인 inference latency를 동시에 고려

 

- Factorized Hierarchical Search Space를 도입하여 NAS 시 모델의 다양성 증대

 

- ImageNet에서 MobileNetV2와 NASNet에 비해 각각 x1.8 그리고 x2.3배 빠른 SOTA 모델 제시

 

- COCO에서 SSD300 모델의 backbone 모델로 MNASNet에서 찾은 모델을 사용했을 때 inference latency와 mAP 모두에서 MobileNetV2 보다 뛰어난 성능 달성

 

Problem Formulation

기본적으로 MNAS에서는 높은 정확도 (high-accuracy)와 낮은 inference latency를 동시에 만족하는 CNN 모델을 찾는 것을 목표로 하고 있습니다. 따라서, 이는 Multi-Objective Search Problem이라고 할 수 있죠. 이 과정에서 MNAS는 기존 Search 기반 방법들과는 다르게 real-world inference latency를 직접적으로 고려하게 됩니다. 이를 위해, 미리 준비된 모바일 디바이스로 샘플링된 모델을 넣고 해당 디바이스에서의 inference latency를 본 논문에서 제안하는 새로운 objective function에 넣어주면 되죠. 

 

 

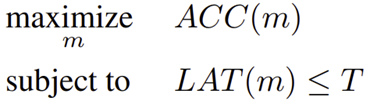
위 수식은 기존 Search 기반 방법들에서 사용되는 latency-constrained objective function입니다. 위 수식에서 $ACC(m)$는 샘플링된 모델 $m$에 대한 타겟 태스크의 정확도, $LAT(m)$는 샘플링된 모델 $m$에 대한 타겟 모바일 플랫폼에서의 inference latency, 그리고 $T$는 타겟 inference latency가 됩니다. 이 최적화 문제의 가장 큰 문제는 단순히 inference latency를 constrained 조건으로만 부여했기 때문에 본 논문에서 목표로 하고자 하는 $ACC(m)$와 $LAT(m)$을 동시에 최적으로 학습할 수 있습니다. 이와 같은 어떤 제한된 자원에 대한 최적화 결과를 Pareto Optimal Solution이라고 하죠. 즉, 위 최적화 문제는 Pareto Optimal Solution을 제공해주지 못합니다. 

 

 

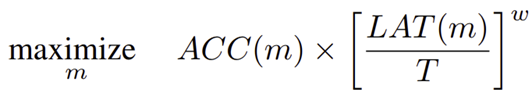
이 문제를 해결하기 위해 본 논문에서는 최적화 식을 제시합니다. 결국 inference latency를 objective function에 넣어줍으로써 동시에 고려할 수 있게 되는 것이죠. 다만, $\frac{LAT (m)}{T}$는 낮아지는 방향으로 학습이 되어야하기 때문에 $w \le 0$인 값으로 사용하게 됩니다. 여기서 $w$는 다음과 같이 정의되는 값입니다. 

 

$$w = \begin{cases} \alpha &\text{ if } LAT(m) \le T \\ \beta &\text{ Otherwise } \end{cases}$$

 

결국에는 $\alpha$와 $\beta$ 값을 정해야하겠죠? 이를 위해 본 논문의 저자들은 경험적으로 inference latency가 2배가 늘어났을 때 모델의 성능이 상대적으로 5%가 향상되었다는 점에 주목하였습니다. 이 결과가 Pareto Optimal Solution을 보장할 수 있도록 하기 위해 다음과 같은 방정식으로 바꿀 수 있습니다. 

 

$$Reward(M1) = a \cdot (1 + 5\%) \cdot \left( \frac{2l}{T} \right)^{\beta} \approx a \cdot \left( \frac{l}{T} \right)^{\beta} = Reward(M2)$$

 

이 방정식을 풀어주면 $\beta = -0.07$을 얻을 수 있습니다. 본 논문에서는 $\alpha = \beta = -0.07$로 고정하여 최적화 문제를 만들었습니다. 

 

 

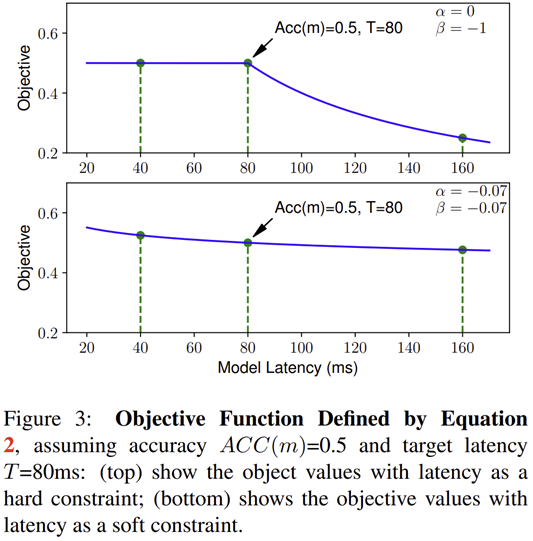
그림 3은 $\alpha$와 $\beta$ 값에 따른 Objective의 감소를 볼수 있습니다. $\alpha = 0, \beta = -1$를 먼저 보겠습니다. 이 말은 $LAT(m) \le T$이면 (샘플링된 모델 $m$의 inference latency가 target inference latency보다 낮은 경우) $\alpha = 0$이고 이는 $w = 0$임을 의미하기 때문에 objective function에서 inference latency $LAT (m)$은 고려되지 않습니다. 이는 기존의 본 논문에서 목표로 하고자 하는 Multi-Objective Search가 수행되지 않을뿐더러 그림 3의 위에 있는 그림과 같이 중간에 non-smoothing point가 생겨 최적화를 어렵게 만들게 됩니다. 따라서, 이러한 문제를 해결할 수 있는 것이 위 방정식을 풀어서 얻은 $\alpha = \beta = -0.07$이 되는 것이죠. 실제로 그림 3의 아래에 있는 그림과 같이 objective function의 수렴은 느리지만 상대적으로 훨씬 부드러워 최적화가 잘 될 수 있을 것 입니다. 

 

Mobile Neural Architecture Search

1). Factorized Hierarchical Search Space 

 

 

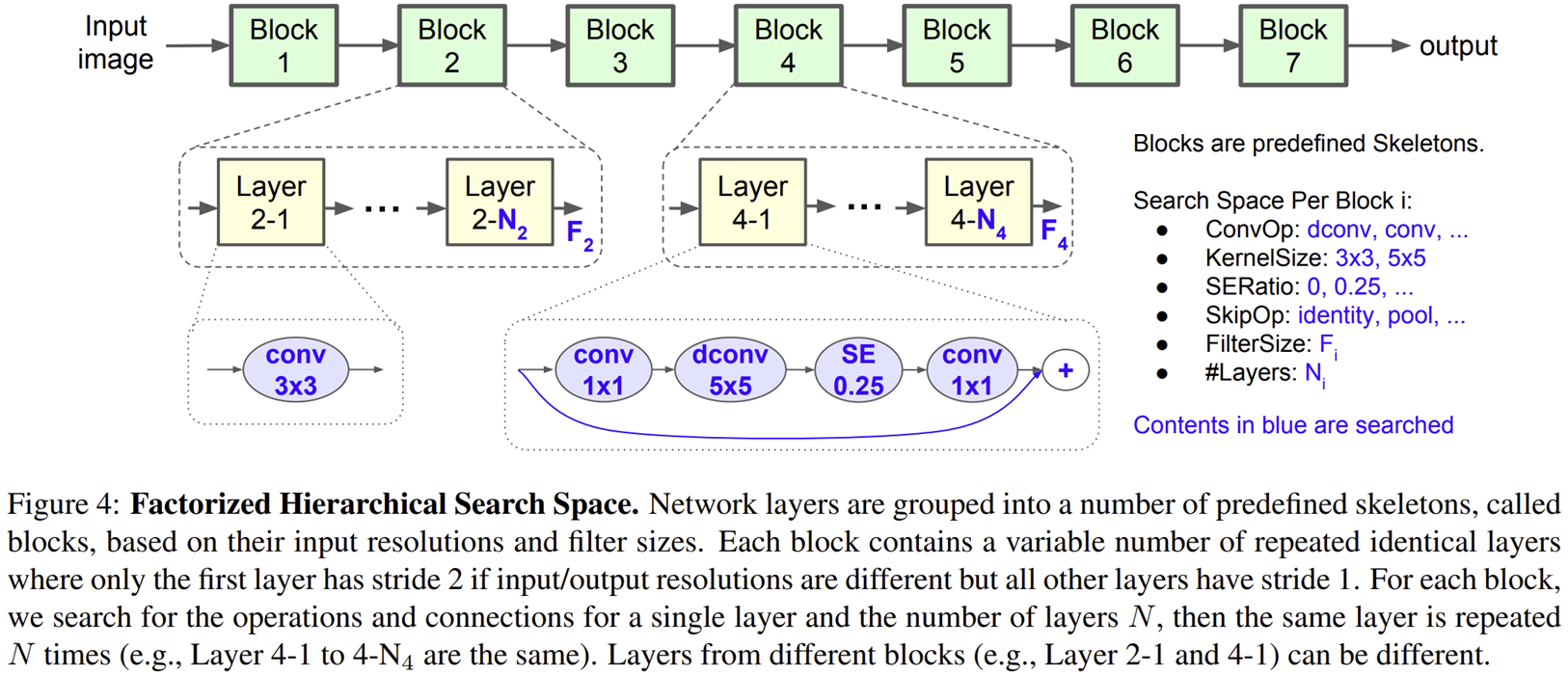
기존 Search 기반 모델들의 Search Space는 몇몇 복잡한 셀을 이용하여 동일한 셀이 반복되어 사용됩니다. 이는 결과적으로 매 샘플링 시 얻는 모델들의 다양성이 떨어진다는 문제점을 얻게 되며 최종적으로 최적화된 모델을 얻기 어려워지게 됩니다. 본 논문에서는 이러한 문제점에 주목하여 CNN 모델을 각각의 독립된 블록 단위로 쪼개줍니다. 그리고 각 블록 단위에서 operation과 connection 탐색을 수행하죠. 이는 서로 다른 블록에서 서로 다른 계층의 구조가 사용되어 보다 다양한 모델이 샘플링될 수 있도록 도와줍니다. 

 

이때, 저희는 모바일 디바이스에서 모델의 성능과 inference latency 간의 적절한 균형을 맞추는 것을 목표로 하기 때문에 Depthwise Separable Convolution을 사용하는 경우 커널 크기 $K$와 필터 크기 (출력 채널의 개수) $N$ 사이의 적절한 선택이 필요합니다. 

 

이를 통해 얻는 최종 Search Space는 $S^{B \times N}$으로 $S$는 각 블록이 가지고 있는 sub-search space의 크기, $B$는 블록의 개수 그리고 $N$은 블록 내의 layer의 개수를 의미합니다. 본 논문에서는 $S = 432, B = 5, N = 3$을 사용하여 총 $10^{13}$ 정도의 검색 공간을 가지게 되죠. 

 

 

위 사진은 MNAS에서 사용하는 연산 및 파라미터의 종류를 보여주고 있습니다. 

 

2). Search Algorithm

최종적으로 저희가 얻은 Search Space는 $10^{13}$으로 기존의 모델들보다 많이 감소하여 강화학습 기반으로 했을 때 효율적으로 최적화할 수 있습니다. 또한, 강화학습은 보상에 대한 사용자화가 쉽기 때문에 다양한 방법들에서 사용되죠.

 

 

그림 1은 MNAS의 전체적인 학습 개략도를 보여주고 있습니다. 구성원은 다음과 같습니다. 

 

- RNN-based Controller

- Trainer to obtain model accuracy

- Mobile phone-based inference engine for measuring the latency

 

또한, 본 논문에서 사용하는 Search Algorithm은 많이 사용되는 Sample-Eval-Update Loop를 사용한다고 합니다. 이를 통해 RNN Controller의 파라미터를 업데이트를 수행하죠. 수행되는 과정은 다음과 같습니다. 

 

STEP1. 현재 파라미터 $\theta$를 기반으로 RNN Controller가 모델 여러 개를 샘플링. 이때, RNN Controller로부터 얻은 Softmax를 기반으로한 token들의 sequence를 예측하면서 수행

 

STEP2. 샘플링된 모델 $m$을 통해 target task 에 대해서 모델을 학습하여 성능 $ACC(m)$을 얻음

 

STEP3. 해당 모델을 실제 모바일 디바이스에서 동작했을 때 나오는 inference latency $LAT(m)$을 얻음

 

STEP4. 본 논문에서 제안하는 Multi-Objective function을 기반으로 Reward $R(m)$을 계산

 

STEP5. Proximal Policy Optimization을 이용해 기대 보상값을 최대화하는 방향으로 RNN Controller의 파라미터 $\theta$를 업데이트

 

END Condition: 반복횟수가 최대에 도달하거나 파라미터 $\theta$가 수렴하는 경우

 

Experiment Results

1). Neural Architecture Search Settings

• Directly perform NAS on ImageNet training set but with fewer training steps (5 epochs)
• Randomly selected 50K images from the training set as the fixed validation set
• Use same RNN Controller as NASNet 
• NAS takes 4.5 days
• 64 TPU V2 
• Measure real-world latency of each sampled model by running it on the single-thread big CPU core of Pixel 1 phones
• RNN Controller samples 8K models during NAS
• Only 15 top-performing models are transferred to the full ImageNet and only 1 model is transferred to COCO

2). Image Classification

• Dataset
  • ImageNet-1K: 1.28 million training images & 50K validation images with 1,000 classes
• Data Augmentation (Same as InceptionNet)
• Optimization: RMSProp
  • momentum: 0.9
  • weight decay: 0.00001
  • learing rate: increase from 0 to 0.256 in the first 5 epochs & decay by 0.97 every 2.4 epochs
• batch size: 4K (4,096)
• epochs: -
• 64 TPU V2 

 

 

 

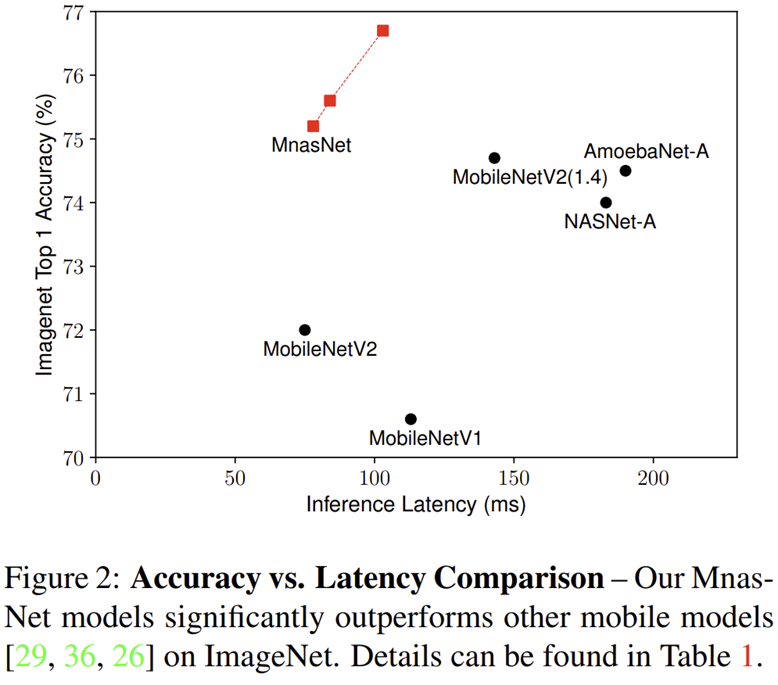
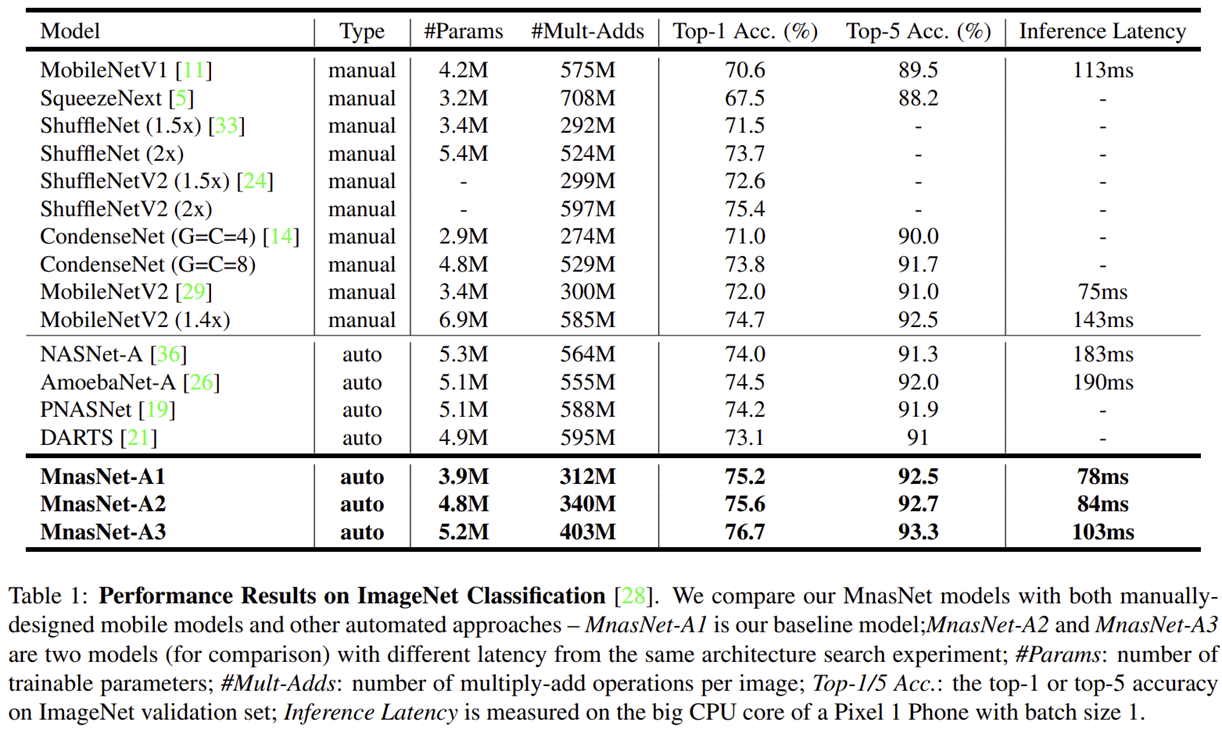
- 그림 2은 MNASNet, MobileNetV1, MobileNetV2,  NASNet, AmoebaNet과의 inference latency vs ImageNet Top-1 Accuracy의 성능을 보여주고 있습니다. 표 1은 보다 다양한 모델들 (SqueenzeNext, ShuffleNet, CondenseNet, PNASNet, DARTS)와의 정량적인 비교를 추가하였습니다. 이때, MNASNet의 가장 소규모 모델인 MNASNet-A1은 MobileNetV2와 유사한 inference latency인 0.75ms를 target inference latency로 두고 탐색을 수행하였습니다.

 

- 유사한 inference latency를 가지는 MobileNetV2와 성능이 약 3% 정도 향상된 것을 볼 수 있습니다. 또한, MNASNet-A1과 유사한  ImageNet Top-1 Accuracy을 가지는 MobileNetV2와 AmoebaNet-A 보다 inference latency는 거의 2배 이상 감소하였습니다.

 

 

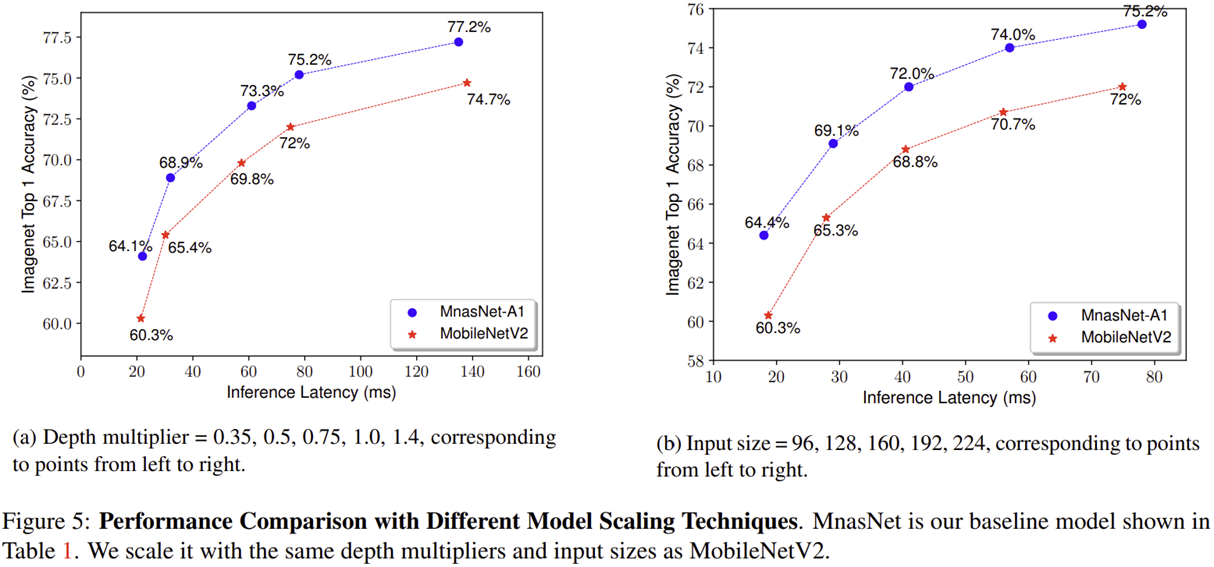
- 그림 5는 MNASNet의 Model Scaling 시얻는 성능을 MobileNetV2와 비교하고 있습니다. (a)는 깊이 (Depth)에 대한 Scaling을 수행했을 때 (b)는 입력 영상의 해상도 (input resolution)에 대한 Scaling을 수행했을 때 입니다.

 

- 두 scaling 방법 모두 MNASNet이 MobileNetV2이 더욱 뛰어난 성능을 보이고 있습니다. 

 

 

 

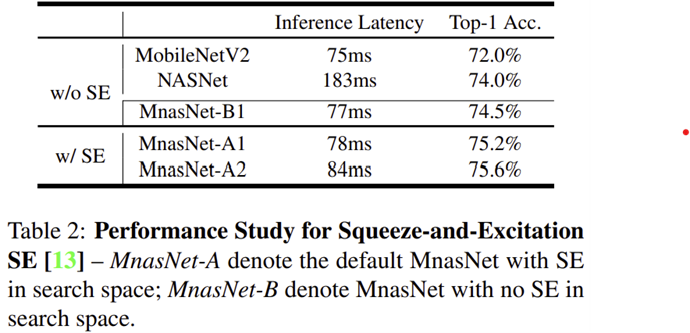
- 표 2는 당시 (2019년)에 각광받던 Squeeze-and-Excitation Block을 Search Space에 추가했을 때 성능을 보여주고 있습니다. 

 

- 기존 모델들인 MobileNetV2와 NASNet은 SE Block을 추가하지 않았지만 SE Block을 추가하여 학습하는 MNASNet은 보다 낮은 inference latency로 높은 성능을 가질 수 있다는 것을 보여주고 있습니다. 이는 SE Block이 NAS 시 성능에 큰 영향을 미치는 것을 보여줍니다. 

 

 

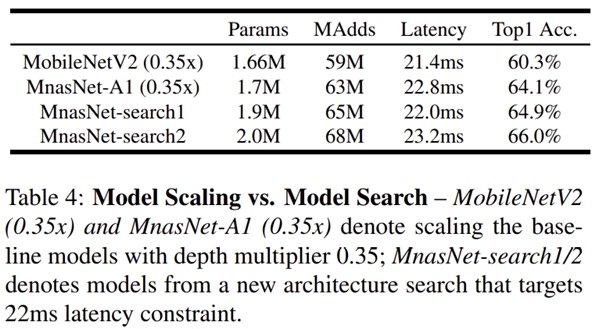
- 표 4는 Scaling과 Search 중 어떤 방법론이 더 좋은지에 대한 성능을 평가하고 있습니다. 

 

- 결과적으로 Search를 적용한 모델들 (MNASNet-Search1과 MNASNet-Search2)에서 더 높은 성능을 얻을 수 있다는 것을 보여줍니다. 

 

3). Object Detection

• Dataset: COCO train2017 (train dataset) & COCO val2017 (evaluation)
  • 118k training images & 5k validation images
• Object Detection model: SSDLite (Modified resource-efficient version of SSD)
• Optimizer: -
  • momentum: -
  • weight decay: -
  • learing rate: -
• batch size: -
• epochs: -
• 64 TPU V2 

 

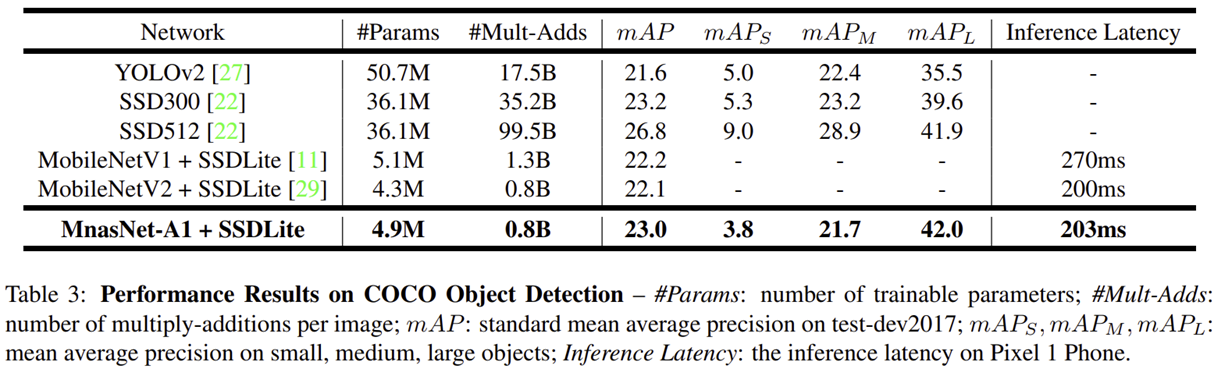
- 표 3은 ImageNet에 학습된 MNASNet을 SSDLite의 backbone 모델로 적용했을 때 기존 모델들과의 비교를 보여주고 있습니다. 

 

- MobileNetV2와 비교해보면 거의 유사한 inference latency로 0.9% 높은 mAP를 얻게 됩니다. 

 

- 기존 SSD 512보다는 성능은 많이 떨어지지만 FLOPs와 파라미터의 개수가 극단적으로 감소한 것을 볼 수 있습니다. 

 

Ablation Study

1). Soft vs Hard Latency Constraint

 

 

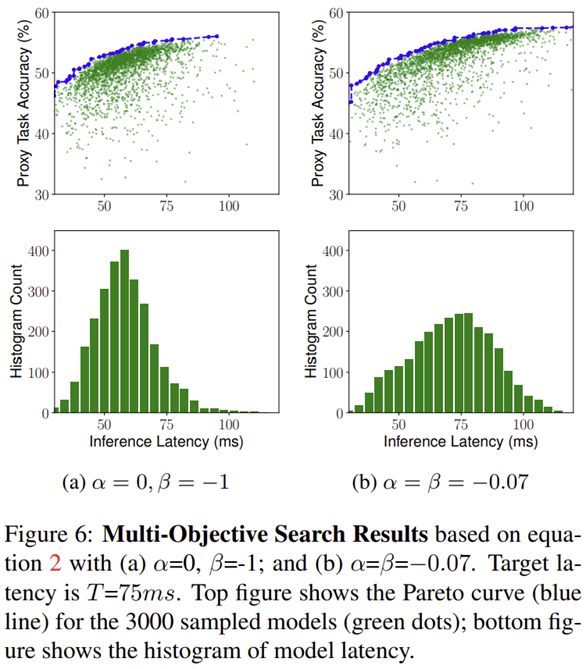
MNASNet의 Pareto Optimal Solution을 보장하기 위해 $\alpha = \beta = -0.07$로 고정한다는 것을 기억하시나요? 본 논문에서는 Hard Latency Constraint ($\alpha = 0, \beta = -1$)와 Soft Latency Constraint ( $\alpha = \beta = -0.07$) 사이의 성능 비교를 보여주고 있습니다. 

 

가장 큰 차이점은 Soft로 하게 되면 샘플링되는 모델들의 inference latency가 MNASNet에서 목표로 하는 target inference latency인 $T = 0.75$ms를 평균으로 하는 가우시안 분포 모양을 따르게 됩니다. 이는 target inference speed를 중심으로 더욱 많은 샘플링된 모델을 유도할 수 있기 때문에 보다 빠른 최적화가 가능하겠죠. 반면에 Hard로 하게 되면 Sampling 시 $LAT(m) \le T$이면 (샘플링된 모델 $m$의 inference latency가 target inference latency보다 낮은 경우) objective function에서 inference latency $LAT (m)$은 고려되지 않아 상대적으로 낮은 inference latency를 가지는 모델들에 대한 샘플링이 수행됩니다. 이는 기본적으로 inference latency가 성능에 직접적으로 영향을 끼친다는 것으로 알려져있기 때문에 target inference latency를 유지하면서 성능을 극대화할 수 있는 Soft Latency Constraint가 보다 최적화에 좋다는 것을 볼 수 있습니다. 

 

2). Disentangling Search Space and Reward

 

표 5는 Single Objective vs Multi Objective 그리고 Cell based search space vs Block based search space의 성능을 비교하고 있습니다. 일단, Multi-Objective 기반 최적화 결과가 inference latency도 동시에 고려할 수 있기 때문에 최종적으로 얻는 inference latency를 Single-Objective에 비해 많이 감소하는 것을 볼 수 있습니다. 하지만, Top-1 성능도 약 2% 정도로 떨어진 것을 볼 수 있죠. 이는 Cell-based로 수행하게 되면 상대적으로 샘플링되는 모델의 다양성을 보장할 수 없기 때문에 발생하는 문제로 볼 수 있습니다. 이때, MNASNet에서 제안하는 블록 기반 Searching Space로 변경하게 되면 보다 다양한 모델들을 샘플링함으로써 sub-optimal에 빠질 확률을 감소시킬 수 있기 때문에 성능이 향상됩니다.