안녕하세요. 지난 포스팅의 [IC2D] Densely Connected Convolutional Networks (CVPR2017)에서는 ResNet을 기반으로 블록 내의 계층 간 연결성을 강화한 DenseNet에 대해서 알아보았습니다. 이를 통해서, 더 낮은 파라미터로 충분히 좋은 성능을 낼 수 있다는 것을 검증하였습니다. 오늘도 ResNet 기반의 새로운 모델인 PyramidNet에 대해서 소개해드리도록 하겠습니다.
Background
ResNet에서는 Residual Block 간의 shortcut path를 도입하여 잔차 학습 (residual learning)이라는 개념을 도입하였습니다. 이를 통해, 기존의 VGGNet과 같이 단순한 모델에서 발생하던 diminish problem이나 gradient vanishing problem 같은 문제들을 해결하였죠. 이는 새로운 모델들의 변형으로 PreAct ResNet, Stochastic Depth, WRN, ResNext, DenseNet과 같은 모델들의 등장을 도와주는 역할을 하게 되어 더 깊고 효율적인 모델을 만드는 것을 목표로 하게 됩니다.
하지만, 여전히 단점 역시 존재합니다. 저희가 하나의 심층 신경망을 구성하게 되면 합성곱 계층과 풀링 계층을 반복하면서 쓰게 되죠. 이 과정에서 풀링 계층은 특징 맵을 subsampling하게 되고 합성곱 계층은 더 많은 특징 맵을 만들게 되죠. 이는 특징 맵의 차원이 굉장히 빠르게 증가하는 원인이 됩니다. 본 논문에서는 이와 같이 너무 빠르게 차원이 증가하여 연산량이 늘어나는 현상을 방지하고자 특징 맵의 차원을 천천히 증가할 수 있도록 도와주는 PyramidNet을 제안합니다.
Network Architecture
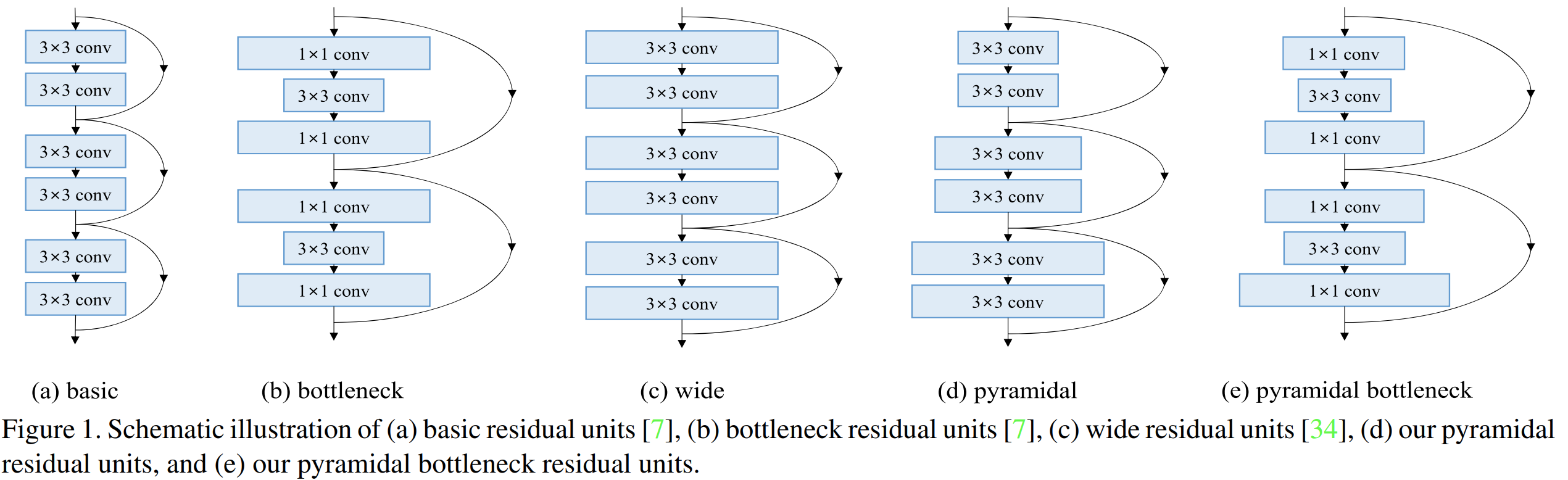
그림1은 residual block의 다양한 변형을 보여주고 있습니다. (a)와 (b)는 기존의 ResNet에서 사용한 Basic Block과 Bottleneck Block입니다. (c)는 WRN에서 제안한 더 많은 필터의 개수를 사용한 블록이죠. (d)와 (e)는 본 논문에서 제안한 PyramidNet에서 사용한 Basic Block과 Bottleneck Block입니다. 그림1에서도 알 수 있듯이 기존의 다른 블록들과의 가장 큰 차이점은 필터의 개수가 점진적으로 늘어나고 있는 것을 볼 수 있습니다.
1). Feature Map Dimension Configuration
일단, 현재 심층 신경망 모델들이 사용하고 있는 블록 내의 특징 맵의 개수를 수학적으로 적어보면 다음과 같습니다.
$$D_{k} = \begin{cases} &16 \text{ if } n(k) = 1 \\ &16 \cdot 2^{n(k) - 2} \text{ if } n(k) \ge 2 \end{cases}$$
여기서, $n(k) \in \{1, 2, 3, 4\}$로 $k$번째 residual unit에 속한 그룹의 인덱스를 의미합니다. $n$번째 그룹에 포함된 residual unit들은 모두 동일한 개수의 특징 맵을 가지고 있습니다. 이를 $N_{n}$이라고 하죠. 첫번째 그룹인 $n(k) = 1$에서는 16개의 특징 맵을 가지고 있습니다. 즉, RGB 영상이 입력되면 16개의 필터를 통해 16개의 특징 맵을 추출하게 되죠. 두번째 그룹부터는 $16 \cdot 2^{n(k) - 2}$로 2의 거듭제곱만큼 훨씬 빠른속도로 특징 맵의 크기가 커지고 있습니다.
PyramidNet에서는 이 부분을 강조하며 특징 맵을 점진적으로 증가시킬 수 있는 두 가지 방법을 제시합니다. 각각 Additive PyramidNet과 Multiplicative PyramidNet 입니다.
(1). Additive PyramidNet
$$D_{k} = \begin{cases} &16 \text{ if } k = 1 \\ &\lfloor D_{k - 1} + \frac{\alpha}{N} \rfloor \text{ if } 2 \le k \le N + 1 \end{cases}$$
여기서, $N$은 residual unit의 전체 개수를 의미합니다. 따라서, $N = \sum_{n = 1}^{4} N_{n}$과 같이 정의할 수 있죠. 식을 잘 보시면 계층별로 $\frac{\alpha}{N}$만큼 늘어나고 있습니다. 그리고 마지막 특징맵의 개수는 $16 + (n - 1) \frac{\alpha}{3}$이 되죠.

표1은 Additive PyramidNet의 구조를 보여주고 있습니다. $N$은 어차피 정해진 값이기 때문에 저희는 $\alpha$에 따라 다양한 형태의 모델을 사용할 수 있다는 것을 알 수 있습니다. 이때, $\alpha$는 너비 (채널의 개수)를 조절하기 때문에 본 논문에서는 widening factor로 정의하여 사용합니다.
(2). Multiplicative PyramidNet
$$D_{k} = \begin{cases} &16 \text{ if } k = 1 \\ &\lfloor D_{k - 1} \cdot \alpha^{\frac{1}{N}} \rfloor \text{ if } 2 \le k \le N + 1 \end{cases}$$
(1)과 같이 덧셈 기반으로 점진적으로 필터의 개수를 늘릴 수도 있지만 (2)와 같이 곱셈 기반으로도 필터의 개수를 점진적으로 늘릴 수 있습니다.
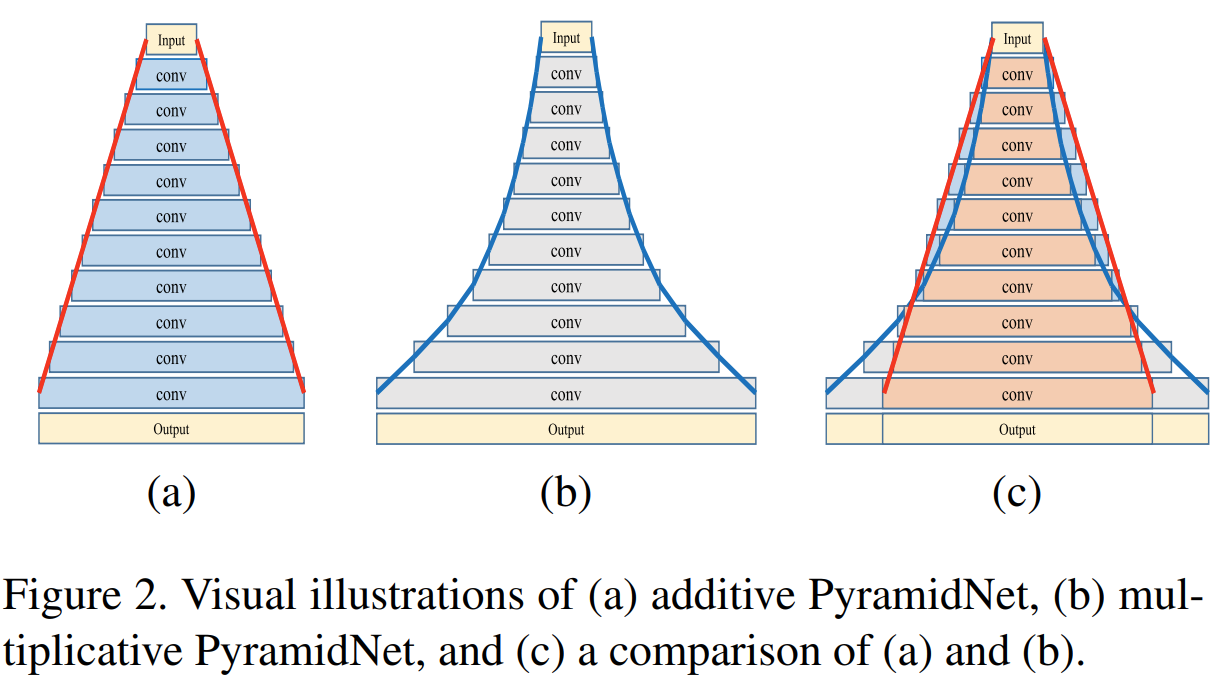
그림2의 (a)는 덧셈 기반, (b)는 곱셈 기반의 PyramidNet 입니다. 그림2를 보시면 왜 PyramidNet이라고 부르게 되는 지 알게 되실 겁니다. 덧셈 및 곱셈 기반 PyramidNet의 가장 큰 차이점은 늘어나는 필터 개수의 선형성입니다. 덧셈 기반은 선형적으로 증가하지만 곱셈 기반은 기하학적으로 증가하죠. 곱셈 기반은 사실 VGGNet이나 ResNet에서도 유사한 방식입니다. 왜냐하면, 출력 계층으로 다가갈 수록 그 채널의 개수가 폭팔적으로 많아지기 때문이죠.
2). Building Block
이제 본격적으로 PyramidNet의 각 블록을 정의해보도록 하겠습니다. 기본적인 순서는 동일하게 $\text{Conv}-\text{ReLU}-\text{BN}$으로 진행됩니다. 이러한 순서는 모델의 수용력을 극대화하는 데 중요하게 작용합니다.
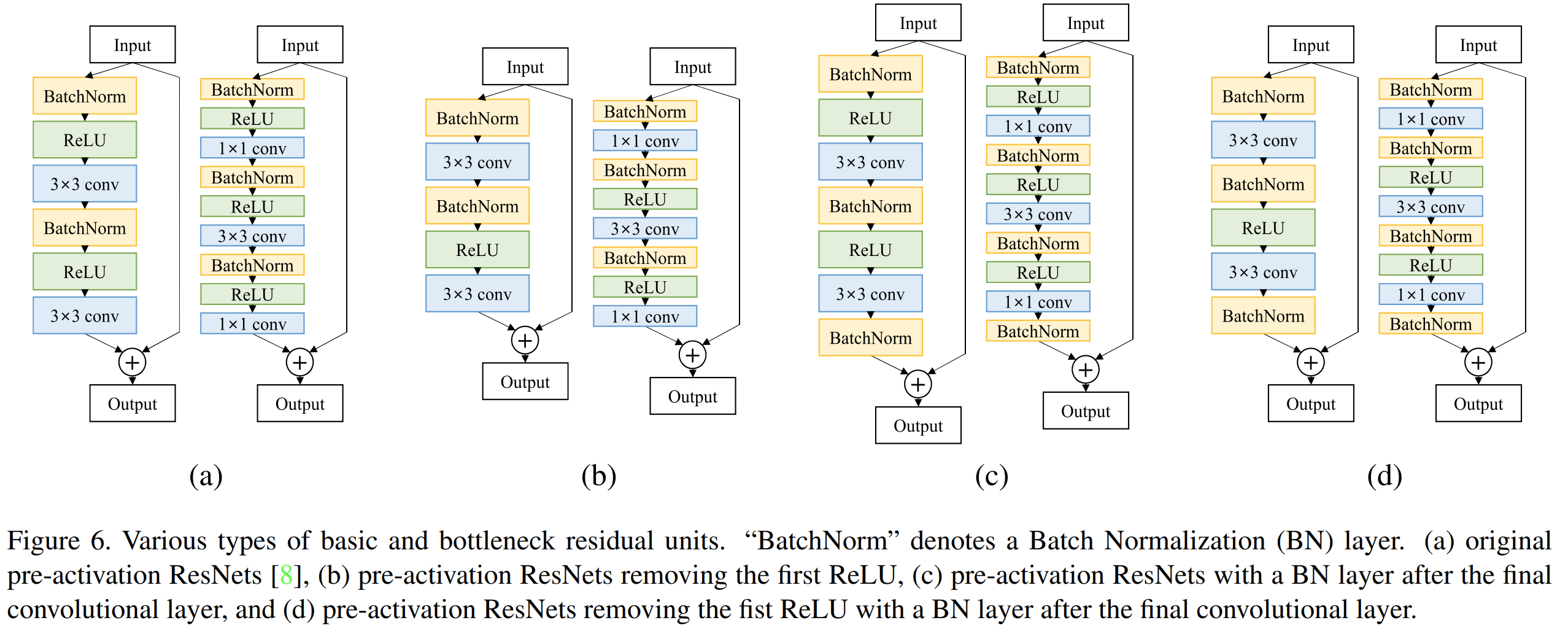
그림6은 한 개의 블록에서 구성할 수 있는 다양한 형태의 residual block을 보여주고 있습니다. (a)는 기존의 ResNet에서 사용한 블록, (b)는 PreAct ResNet에서 가장 앞의 ReLU를 제거한 블록, (c)는 PreAct ResNet에서 마지막 합성곱 계층 이후에 배치 정규화 계층을 추가한 블록, (d)는 (c) 블록에서 앞의 ReLU를 제거한 블록입니다.
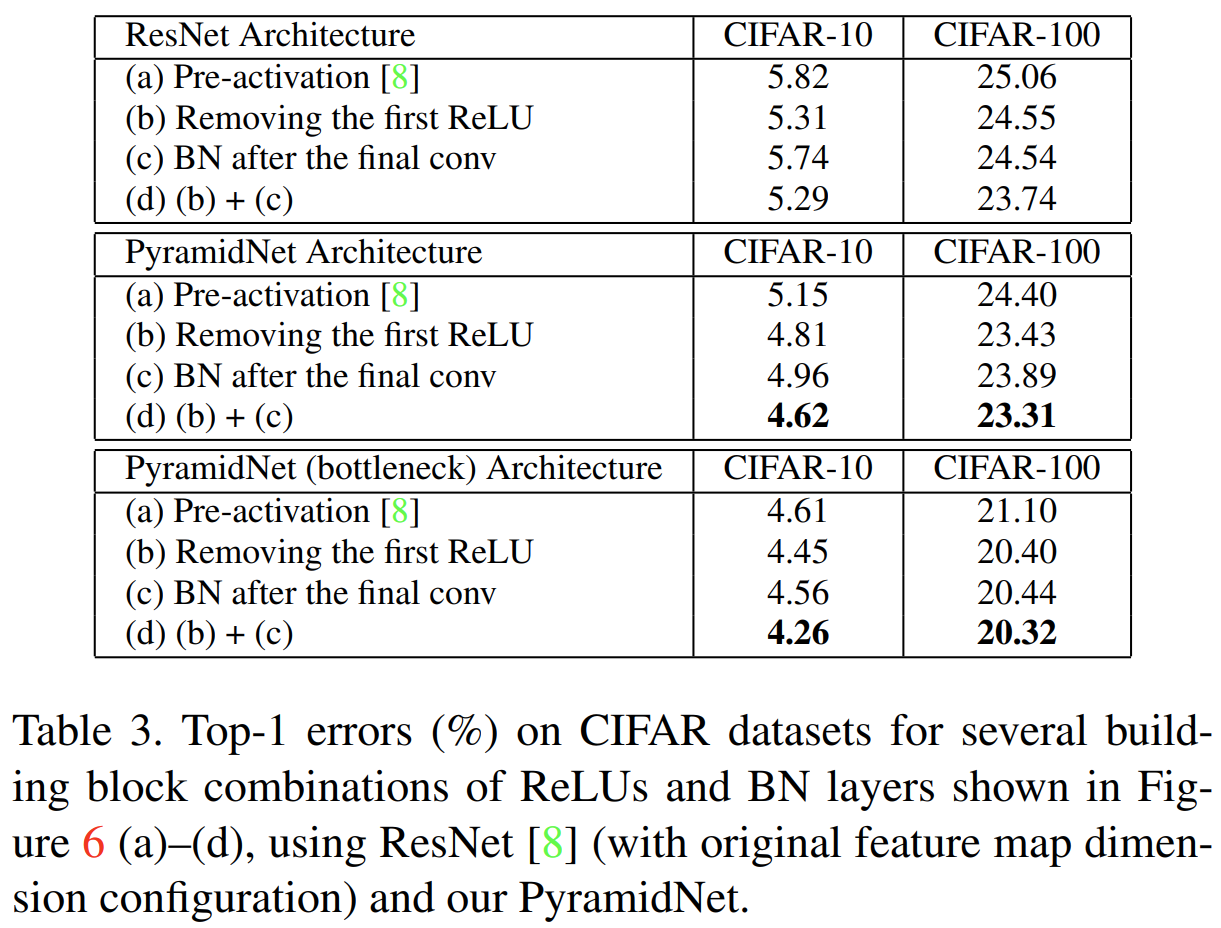
표3은 그림6에서 보여준 다양한 블록에 따른 성능을 표시합니다. 모든 경우에서 (d)가 가장 좋은 성능을 보이고 있기 때문에 앞으로 다른 모델과 비교할 때는 (d)를 사용한 PyramidNet과 비교합니다.
3. Zero-padded Shortcut Connection
마지막으로 한 가지 중요한 사실이 있습니다. PyramidNet에서는 점진적으로 특징 맵의 개수를 늘리고 있습니다. 이 경우에 입력 특징맵 (skip path)의 크기와 출력 특징맵 (residual path)의 크기가 안맞기 때문에 더할 수가 없습니다. PyramidNet에서는 이를 해결하기 위해 zero-padded identity-mapping shortcuts이라는 것을 제안합니다. 아마도 $1 \times 1$ 합성곱 계층으로 크기를 조절하면 되는 거 아닌가 싶을 수도 있겠지만 저희는 PreAct ResNet에 대해서 공부할 때 skip connection이 identity mapping으로 두는 것이 얼마나 중요한 지를 보았습니다.
zero-padded identity-mapping shortcuts의 효과를 검증하기 위해 $n$번째 그룹에 포함된 $k$번째 residual unit $\mathbf{x}_{k}^{l}$에 적용해보면 다음과 같습니다. 여기서, $l$은 $\mathbf{x}_{k}$의 $l$번째 특징 맵이라는 것을 의미합니다.
$$\mathb{x}_{k}^{l} = \begin{cases} \mathbf{F}_{(k, l)} (\mathbf{x}_{k - 1}^{l}) + \mathbf{x}_{k - 1}^{l} \text{ if } 1 \le l \le D_{k - 1} \\ \mathbf{F}_{(k, l)} (\mathbf{x}_{k - 1}^{l}) \text{ if } D_{k - 1} < l \le D_{k} \end{cases}$$
여기서, $\mathbf{F}_{(k, l)} ( \cdot )$은 $k$번째 residual unit의 $l$번째 residual function으로 정의되고 $D_{k}$는 $k$번째 residual unit의 채널 개수를 의미합니다.
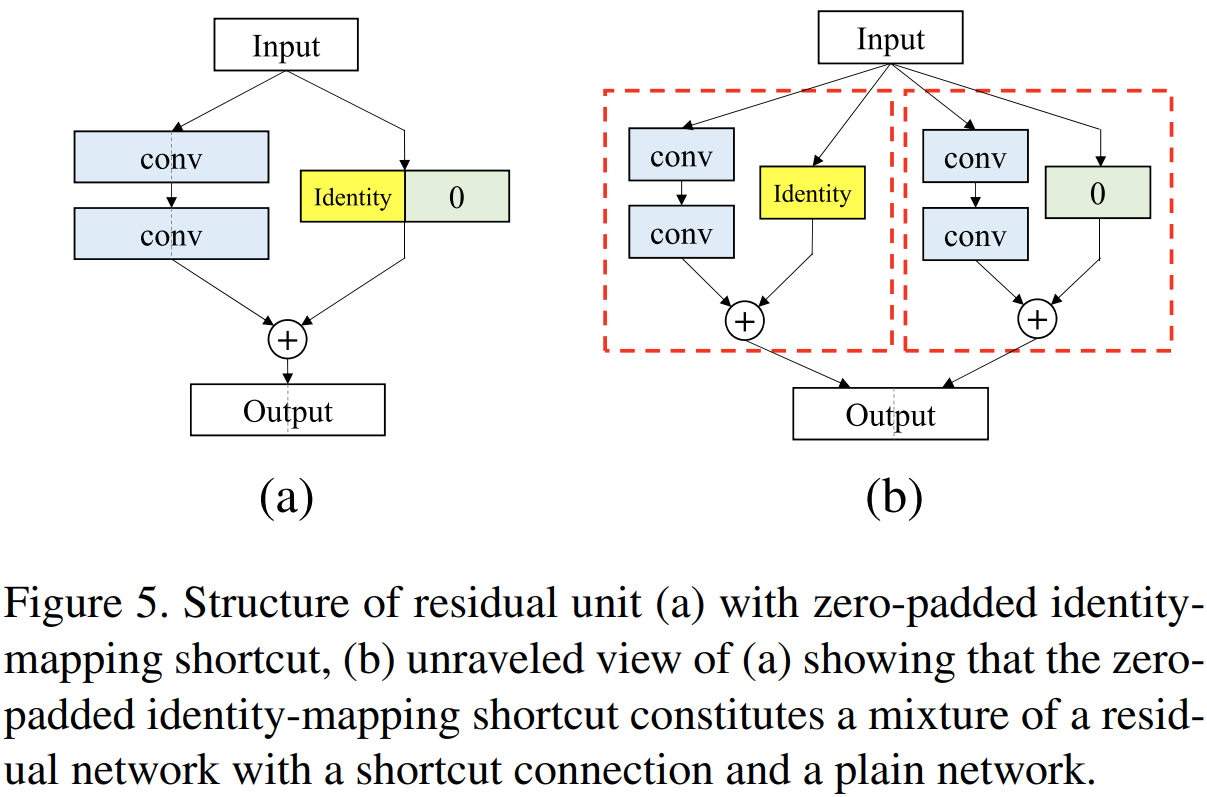
그림5는 PyramidNet에서 제안한 Zero-padded Shortcut Connection의 블록 다이어그램입니다. 그림으로 보시면 더욱 쉽게 이해할 수 있죠. 핵심은 identity를 건들이지 않는 것이기 때문에 그냥 residual path와 identity path의 채널 차이만큼 0 (zero)를 추가 (padding)하여 더해주는 것을 의미합니다. (b)는 이를 unravel로 표현한 것인데 잘 보시면 zero path가 identity에 영향을 주지 않기 때문에 identity의 중요성을 살릴 수 있음을 보여주고 있습니다.

표2는 다양한 shortcut에 따른 성능을 비교하고 있습니다. 일단, shortcut에 projection을 적용하면 성능이 떨어지는 것을 볼 수 있습니다. 하지만, Zero-padded Shortcut Connection은 성능이 유지되고 있죠.
Experiment Results
본 논문에서는 CIFAR10, CIFAR100, ImageNet에 대해서 실험을 진행하였습니다.
1). Classification Results in CIFAR
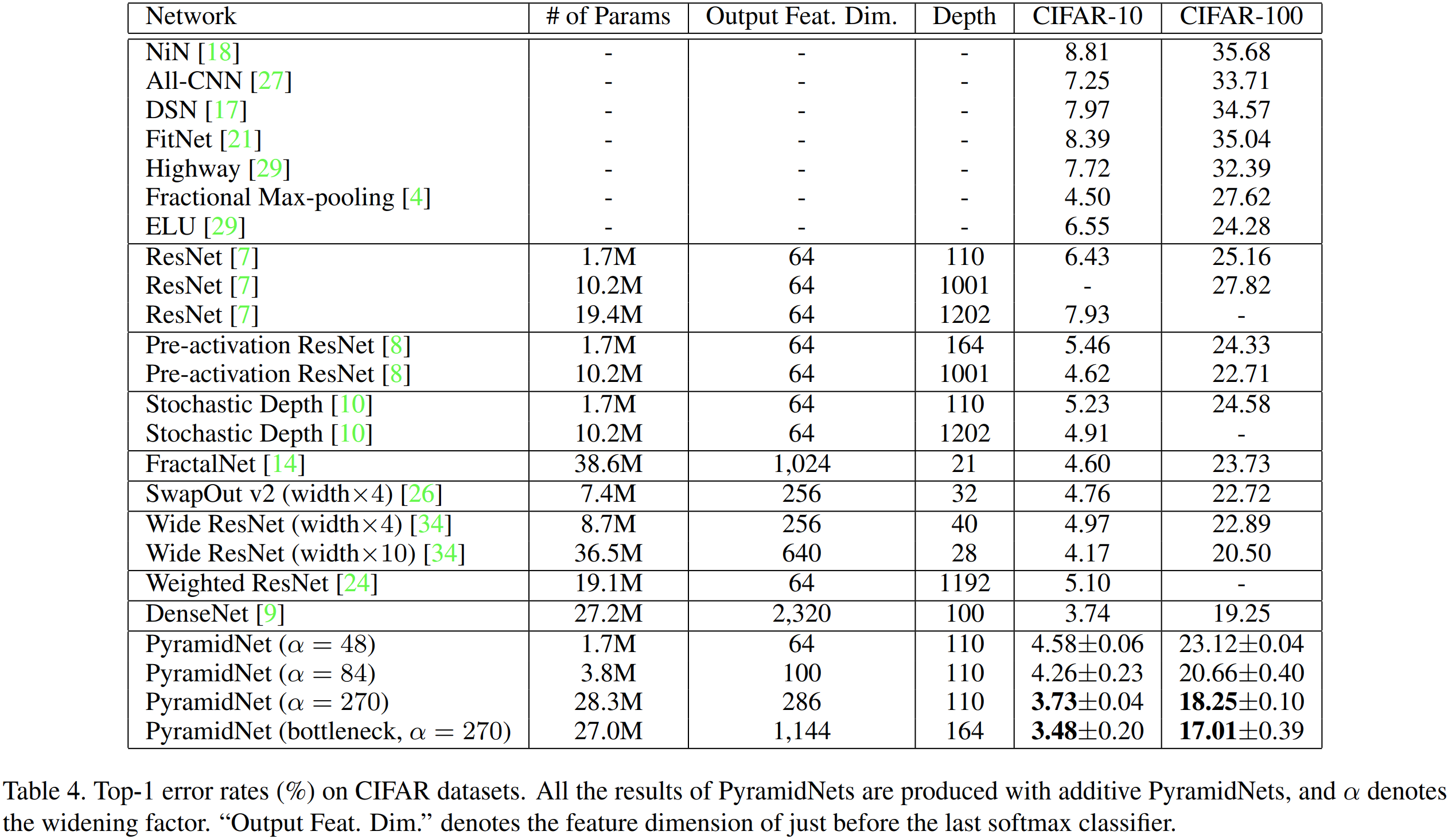
제일 먼저, CIFAR에서 성능을 비교해보면 기존의 ResNet보다도 성능이 훨씬 높습니다. WRN과 비교해보면 파라미터 개수는 훨씬 적지만 성능은 거의 유사한 것을 볼 수 있죠. 즉, PyramidNet은 WRN보다 훨씬 효율적인 모델이라는 것을 의미합니다. 또한, DenseNet과도 성능을 비교했네요. DenseNet의 성능은 좋지만 그 연결성으로 인해 효율적이지 않은 모습을 보여주고 있습니다.
2). Classification Results in ImageNet
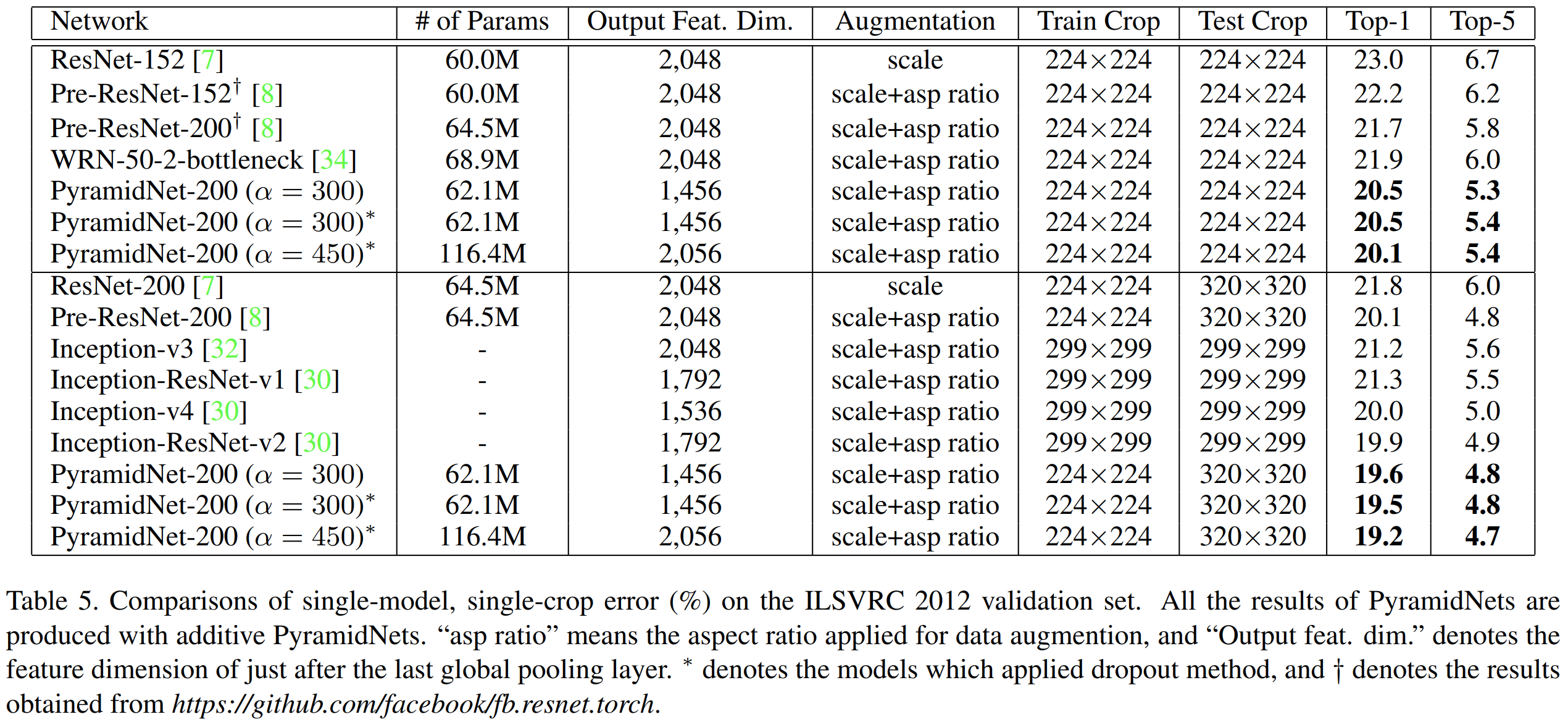
Implementation Code
import torch
import torch.nn as nn
class BasicBlock(nn.Module):
outchannel_ratio = 1
def __init__(self, in_channels, out_channels, stride=1, downsample=False):
super(BasicBlock, self).__init__()
# residual function
self.residual_function = nn.Sequential(
nn.BatchNorm2d(in_channels),
nn.Conv2d(in_channels, out_channels, kernel_size=(3, 3), stride=(stride, stride), padding=(1, 1), bias=False),
nn.BatchNorm2d(out_channels), nn.ReLU(inplace=True),
nn.Conv2d(out_channels, out_channels, kernel_size=(3, 3), padding=(1, 1), bias=False),
nn.BatchNorm2d(out_channels)
)
self.downsample = downsample
self.stride = stride
def forward(self, x):
residual = self.residual_function(x)
if self.downsample is not None:
shortcut = self.downsample(x)
featuremap_size = shortcut.size()[2:4]
else:
shortcut = x
featuremap_size = residual.size()[2:4]
batch_size = residual.size()[0]
residual_channel = residual.size()[1]
shortcut_channel = shortcut.size()[1]
if residual_channel != shortcut_channel:
padding = torch.autograd.Variable(torch.cuda.FloatTensor(batch_size, residual_channel - shortcut_channel, featuremap_size[0], featuremap_size[1]).fill_(0))
residual += torch.cat((shortcut, padding), 1)
else:
residual += shortcut
return residual
class BottleNeckBlock(nn.Module):
outchannel_ratio = 1
def __init__(self, in_channels, out_channels, stride=1, downsample=False):
super(BottleNeckBlock, self).__init__()
self.residual_function = nn.Sequential(
nn.BatchNorm2d(in_channels),
nn.Conv2d(in_channels, out_channels, kernel_size=1, bias=False),
nn.BatchNorm2d(out_channels), nn.ReLU(inplace=True),
nn.Conv2d(out_channels, out_channels, stride=stride, kernel_size=3, padding=1, bias=False),
nn.BatchNorm2d(out_channels), nn.ReLU(inplace=True),
nn.Conv2d(out_channels, out_channels, kernel_size=1, bias=False),
nn.BatchNorm2d(out_channels),
)
self.downsample = downsample
self.stride = stride
def forward(self, x):
residual = self.residual_function(x)
if self.downsample is not None:
shortcut = self.downsample(x)
featuremap_size = shortcut.size()[2:4]
else:
shortcut = x
featuremap_size = residual.size()[2:4]
batch_size = residual.size()[0]
residual_channel = residual.size()[1]
shortcut_channel = shortcut.size()[1]
if residual_channel != shortcut_channel:
padding = torch.autograd.Variable(torch.cuda.FloatTensor(batch_size, residual_channel - shortcut_channel, featuremap_size[0], featuremap_size[1]).fill_(0))
residual += torch.cat((shortcut, padding), 1)
else:
residual += shortcut
return residual
class PyramidNet(nn.Module):
def __init__(self, num_channels, num_classes, depth, alpha, bottleneck=False):
super(PyramidNet, self).__init__()
self.inplanes = 16
if bottleneck:
n = int((depth - 2) / 9)
block = BottleNeckBlock
else:
n = int((depth - 2) / 6)
block = BasicBlock
self.add_rate = alpha / (3 * n)
self.input_feature_dim = self.inplanes
self.conv1 = nn.Conv2d(num_channels, self.input_feature_dim, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
self.bn1 = nn.BatchNorm2d(self.input_feature_dim)
self.feature_dim = self.input_feature_dim
self.layer1 = self.pyramidal_make_layer(block, n)
self.layer2 = self.pyramidal_make_layer(block, n, stride=2)
self.layer3 = self.pyramidal_make_layer(block, n, stride=2)
self.final_featuremap_dim = self.input_featuremap_dim
self.bn_final = nn.BatchNorm2d(self.final_featuremap_dim)
self.relu_final = nn.ReLU(inplace=True)
self.avgpool = nn.AvgPool2d(8)
self.fc = nn.Linear(self.final_featuremap_dim, num_classes)
def pyramidal_make_layer(self, block, block_depth, stride=1):
downsample=False
if stride != 1:
downsample = nn.AvgPool2d((2, 2), stride=(2, 2), ceil_mode=True)
layers = []
self.feature_dim = self.feature_dim + self.add_rate
layers.append(block(self.input_feature_dim, int(round(self.feature_dim)), stride, downsample))
for i in range(1, block_depth):
temp_feature_dim = self.feature_dim + self.add_rate
layers.append(block(int(round(self.feature_dim)) * block.outchannel_ratio, int(round(temp_feature_dim)), 1))
self.feature_dim = temp_feature_dim
self.input_feature_dim = int(round(self.feature_dim)) * block.outchannel_ratio
return nn.Sequential(*layers)