안녕하세요. 지난 포스팅의 [IC2D] MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications (arxiv2017)에서는 휴대장치에서도 빠르게 동작할 수 있는 효율적인 모델인 MobileNet에 대해서 소개해드렸습니다. 저희는 이때 처음으로 nn.Conv2d의 인자인 groups에 대해서 알게 되었습니다. MobileNet에서는 이를 depthwise로 사용하여 연산량을 낮추는 데 사용하였죠. 오늘은 ResNet과 InceptionNet을 기반으로 연구된 ResNext에 대해서 소개해드리도록 하겠습니다.
Aggregated Residual Transformations for Deep Neural Networks
We present a simple, highly modularized network architecture for image classification. Our network is constructed by repeating a building block that aggregates a set of transformations with the same topology. Our simple design results in a homogeneous, mul
arxiv.org
Background
이름에서도 보시다시피 ResNext는 ResNet 기반의 모델로 저번에 소개해드린 WRN과 같이 모델의 깊이보다 다른 요소에 집중하여 성능을 향상하는 모델입니다. ResNext는 지난번에 설명드린 2가지의 모델로부터 영감을 얻었습니다. 바로 ResNet과 InceptionNet이죠.
InceptionNet은 입력 특징맵에 병렬적으로 다양한 필터 크기를 가지는 합성곱 연산을 적용하여 다양한 스케일의 공간정보를 추출하게 됩니다. 이러한 구조를 Split-Transformation-Merge 구조라고 부르도록 하겠습니다. 하지만 이러한 구조는 동시에 합성곱 연산을 여러 번 수행해야 하기 때문에 계산량이 매우 커질 수밖에 없습니다. 물론 Inception Module에서는 이를 줄이고자 앞에 $1 \times 1$ 필터 크기의 합성곱 연산을 먼저 적용하여 차원 축소를 한 뒤 합성곱을 수행하였지만 여전히 계산 비용은 큰 편입니다.
본 논문에서는 InceptionNet 구조의 Split-Transformation-Merge 구조를 차용하여 좀 더 단순하게 모델을 구성하고자 합니다. 따라서, InceptionNet에서의 Transformation 과정을 VGGNet이나 Residual Block과 같은 것으로 대체하게 되는 것이죠. 이때, 각 branch에서의 출력 특징맵을 concatenate하게 되면 그 차원이 엄청나게 커지기 때문에 이를 방지하게 위해 단순히 원소별 합을 통해 특징맵을 추출합니다. 이 과정에서 본 논문은 Cardinality라는 개념에 대해서 언급합니다. 이는 기존의 ResNet에서 강조했던 깊이 (depth)나 WRN에서 강조한 너비 (width)와는 다른 새로운 개념으로 이를 통해 좀 더 효율적인 방법으로 성능을 향상하게 됩니다.
Method
방금도 언급했다싶이 본 논문에서는 단순함을 추구하기 때문에 각 branch는 전부 동일한 구조를 사용하게 됩니다. 그중에서 후보가 될 수 있는 것은 VGGNet과 ResNet에서 사용한 블록이 되겠네요. 단, 각 branch는 다음의 조건을 만족해야 합니다.
1). 각 branch에서 동일한 크기의 특징 맵을 출력한다면 branch 내의 각 블록은 모두 동일한 하이퍼파라미터 (너비, 필터 크기)를 가져야 한다.
2). 각 branch에서 특징 맵의 해상도가 2배씩 감소할 때 너비는 2배씩 증가해야 한다.
2) 번 규칙을 통해 모든 블록에서 동일한 연산량을 가질 수 있는 것을 보장합니다. 위의 조건을 만족하면 template module이라고 부르게 되죠.
1). Revisiting Simple Neurons
합성곱 계층에 바로 위 template module을 적용하기 전에 단순한 MLP 구조에 먼저 적용해 보도록 하겠습니다. 단순한 MLP에서는 다음과 같이 출력값이 나옵니다.
$$\sum_{i = 1}^{D} w_{i} x_{i}$$
즉, 각 노드의 가중치 $w_{i}$와 입력값 $x_{i}$에 대한 내적 (inner product)라고 해석할 수 있죠.
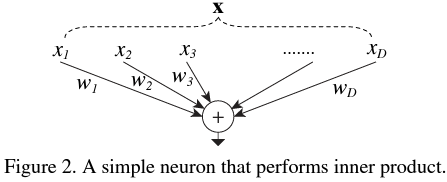
위 그림은 MLP를 그림으로 도식화한 모습입니다. 여기서 Split은 입력벡터 $\mathbf {x} = [x_{1}, \dots, x_{D}]$를 작은 차원으로 분해하는 것을 의미합니다. Transformation은 작은 차원으로 쪼개진 각각의 저 차원 벡터 $x_{1}, \dots, x_{D}$를 이용해서 $w_{1} x_{1}, \dots, w_{D} x_{D}$로 변환하는 과정을 의미하죠. 마지막으로 merge는 각 노드의 출력을 하나로 concatenate 하거나 더하는 것을 의미하죠.
2). Aggregated Transformations
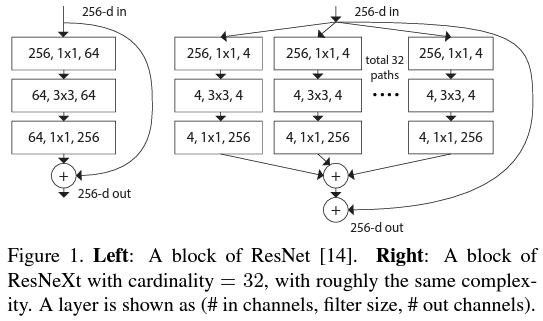
위 그림은 ResNet과 ResNext를 비교한 그림입니다. 본격적으로 설명하기 전에 드디어 cardinality $C$가 무엇인지 알려드려야겠군요. 사실 아주 쉽습니다. 위 그림에 보시면 256개 채널의 특징맵이 $1 \times 1$ 필터 크기의 합성곱을 이용해 각 branch의 4개의 채널을 가지는 저 차원의 특징맵을 분해되어 총 32개의 branch를 가집니다. 이와 같이 몇 개의 branch인지가 곧 cardinality라고 부르죠. 수학적으로 cardinality라고 한다면 집합의 크기를 의미합니다. 본 논문에서는 1개의 residual block에 포함된 branch의 개수를 cardinality라고 정의한 것이죠. (이 부분을 설명하려고 본 논문에서는 1884년에 출판에 게오르크 칸토어의 논문을 인용합니다;;)
이제 저희는 각 branch를 함수로 표현하여 $\mathcal {T}_{i}$라고 하겠습니다. 그러면 ResNext의 Residual 연산은 다음과 같이 정의할 수 있죠.
$$\mathcal {F}(\mathbf {x}) = \sum_{i = 1}^{C} \mathcal {T}_{i}(\mathbf {x})$$
마지막으로 이를 Residual Function으로 구성해 주면 됩니다.
$$\mathbf {y} = \mathbf {x} + \mathcal{F}(\mathbf{x}) = \mathbf{x} + \sum_{i = 1}^{C} \mathcal {T}_{i}(\mathbf {x})$$
물론, 그림 1과 같이 $\mathcal {T}_{i}$를 정의하여 사용할 수도 있겠지만 물론 다르게도 사용할 수 있습니다.
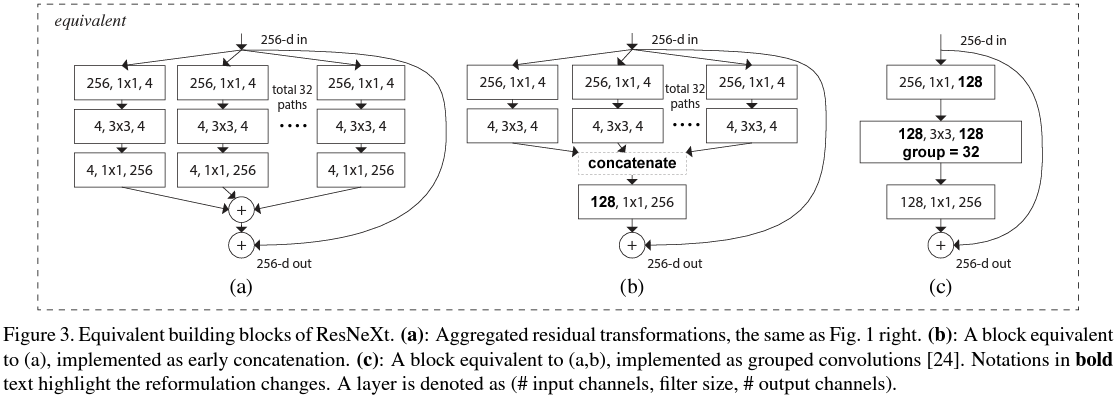
그림 3은 ResNext 모듈을 동일하지만 단순한 시켜 표현하는 과정입니다. 그림 3의 (a)는 그림1의 (b)와 동일합니다. 잘 보시면 각 branch의 결과를 $1 \times 1$ 합성곱 연산을 적용한 뒤 원소별 합을 수행하는 것을 볼 수 있습니다. 사실 이것은 그림3의 (b)와 같이 $3 \times 3$ 합성곱 연산을 적용한 결과를 concat 한 뒤 $4 \times 32 = 128$개의 채널을 입력으로 받고 256개의 채널의 출력으로 갖는 $1 \times 1$ 합성곱 연산을 수행하는 것과 동일합니다. 그리고 이것은 역시 256개의 채널을 갖는 입력 특징맵을 $1 \times 1$ 합성곱 연산을 이용해서 128개의 채널을 갖게 만든 뒤 4개의 채널씩 총 32개의 branch로 나누어 연산하는 것과 동일하므로 nn.Conv 함수의 groups 인자를 32로 둠으로써 더욱 쉽게 구현할 수 있죠.
일반적인 합성곱 연산과 달리 위와 같이 groups를 정의하여 합성곱을 수행하는 경우 grouped convolution이라고 정의합니다. MobileNet에서 보았던 depthwise convolution은 grouped convolution의 특수한 경우가 되겠네요.
3). Model Capacity

이번 절에서는 모델의 복잡도와 파라미터의 개수는 유지하며 cardinality를 증가시킴으로써 성능을 향상하는 법에 대해서 언급합니다. 본 논문에서는 위 그림과 같이 cardinality에 따른 복잡도를 유지시키기 위해 모델의 다른 하이퍼파라미터인 깊이와 너비를 조절하였습니다. 이를 통해 파라미터는 총 $70k$, 계산복잡도 FLOPs는 $0.22 billion$만큼 유지한 것을 볼 수 있습니다. 이때, cardinality를 도입했을 때 파라미터의 개수를 구하는 방법에 대해서 설명해 드리도록 하겠습니다. 가장 간단한 경우로 그림 1 (a)와 같이 ResNet의 bottleneck block의 파라미터의 개수를 구하기 위해 각 계층을 정리하면 다음과 같습니다.
1). $(256, 1 \times 1, 64)$ : 256개의 채널을 갖는 특징 맵을 입력으로 받아 $1 \times 1$ 합성곱 연산을 적용하여 64개의 채널을 갖는 특징 맵으로 변환 $ \Rightarrow 256 \times 1 \times 1 \times 64$
2). $(64, 3 \times 3, 64)$ : 64개의 채널을 갖는 특징 맵을 입력으로 받아 $3 \times 3$ 합성곱 연산을 적용하여 64개의 채널을 갖는 특징 맵으로 변환 $ \Rightarrow 64 \times 3 \times 3 \times 64$
3). $(64, 1 \times 1, 256)$ : 64개의 채널을 갖는 특징 맵을 입력으로 받아 $1 \times 1$ 합성곱 연산을 적용하여 256개의 채널을 갖는 특징 맵으로 변환 $ \Rightarrow 64 \times 1 \times 1 \times 256$
따라서 각 계층의 파라미터 개수를 합하면 거의 70,000개 정도가 됩니다. 이제 여기서 cardinality를 추가해 보도록 하죠. 그림 1 (b)를 기준으로 설명드리도록 하겠습니다. 어차피 각 branch는 모두 동일한 변환을 수행하므로 하나의 branch에 대한 파라미터 개수를 구한 뒤 cardinality만큼 곱하면 1개의 residual block에 대한 파라미터 개수를 알 수 있습니다.
1). $(256, 1 \times 1, 4)$ : 256개의 채널을 갖는 특징 맵을 입력으로 받아 $1 \times 1$ 합성곱 연산을 적용하여 4개의 채널을 갖는 특징 맵으로 변환 $ \Rightarrow 256 \times 1 \times 1 \times 4$
2). $(4, 3 \times 3, 4)$ : 4개의 채널을 갖는 특징 맵을 입력으로 받아 $3 \times 3$ 합성곱 연산을 적용하여 4개의 채널을 갖는 특징 맵으로 변환 $ \Rightarrow 4 \times 3 \times 3 \times 4$
3). $(4, 1 \times 1, 256)$ : 4개의 채널을 갖는 특징 맵을 입력으로 받아 $1 \times 1$ 합성곱 연산을 적용하여 256개의 채널을 갖는 특징 맵으로 변환 $ \Rightarrow 4 \times 1 \times 1 \times 256$
그러면 1개의 branch에 대해서 2,192개의 파라미터를 가지므로 총 32개의 branch에 대해서는 거의 70,000개의 파라미터를 갖는 것을 볼 수 있죠. 이를 일반화시켜서 cardinality가 $C$, 중간 계층의 채널 개수를 $d$라고 하면 다음과 같이 파라미터 개수를 계산할 수 있습니다.
$$C \cdot (256 \cdot d + 3 \cdot 3 \cdot d \cdot d + d \cdot 256)$$
그림 1 (b)는 $C = 32, d = 4$인 경우를 의미하죠.
ResNext Architecture
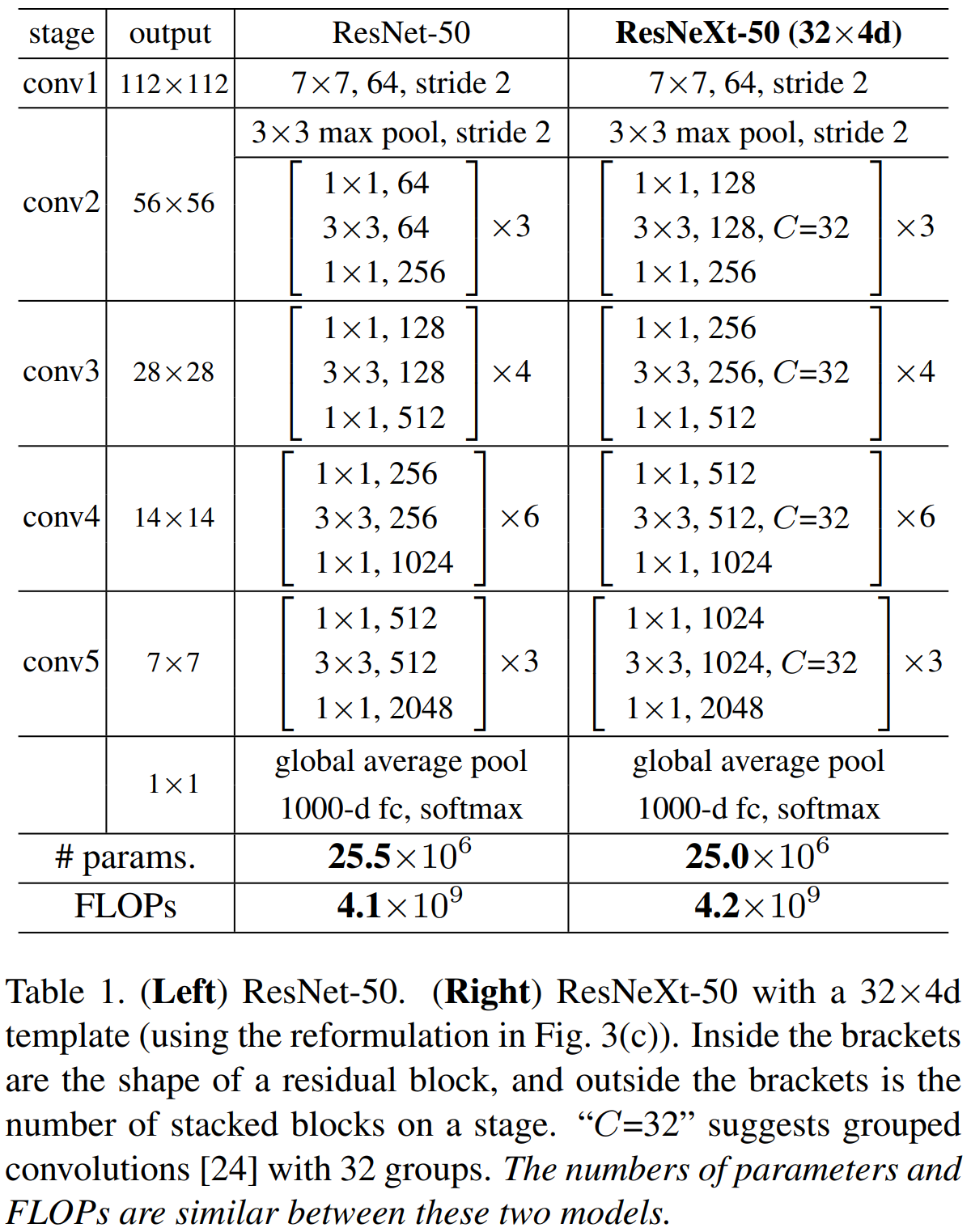
표 1은 ResNet과 ResNext의 구조적인 비교를 하고 있습니다. 연산량과 파라미터의 개수는 큰 차이가 없습니다.
Experiment Results
본 논문에 실험에서 cardinality $C$그리고 inter channel $d$에 대해서 50개의 계층을 가지는 ResNext를 ResNext-50($C \times d$)와 같이 표시하니 참고하시길 바랍니다.
1). Cardinality vs Width
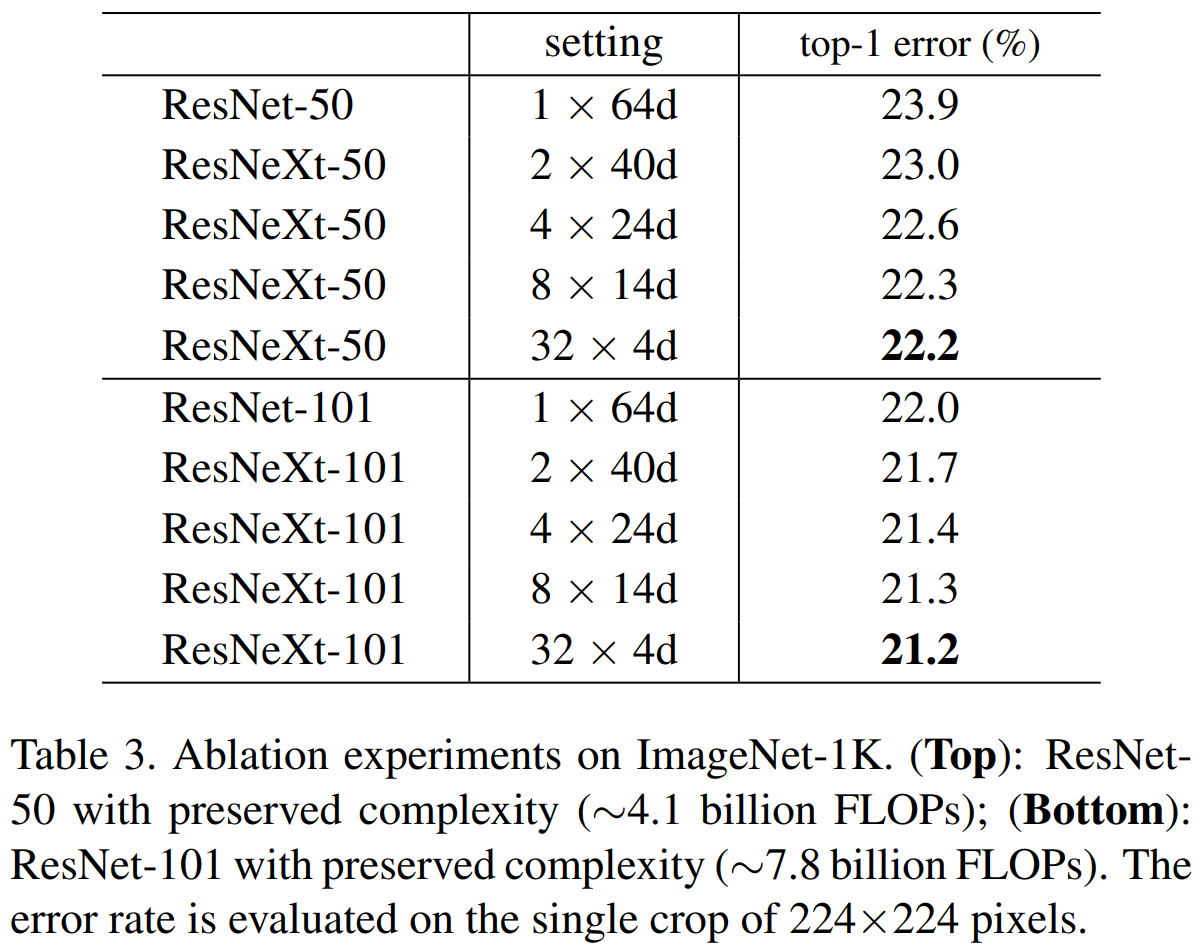
표 3은 Cardinality $C$를 1, 2, 4, 8, 32로 바꾸었을 때 성능변화를 50개의 계층을 가질 때와 101개의 계층을 가질 때로 나누어 비교하고 있습니다. 기본적으로 모든 경우의 파라미터와 연산량이 거의 유사한 점을 고려하면 $C = 32$를 했을 때 성능이 $C = 1$일 때보다 약 1.7% 향상하는 것을 볼 수 있습니다. 한 가지 놀라운 점은 101개의 계층을 가진 ResNet101과 ResNext50($32 \times 4d$)와 거의 0.2% 차이밖에 나지 않는 것을 볼 수 있죠.
2). Increasing Cardinality vs Deeper/Wider
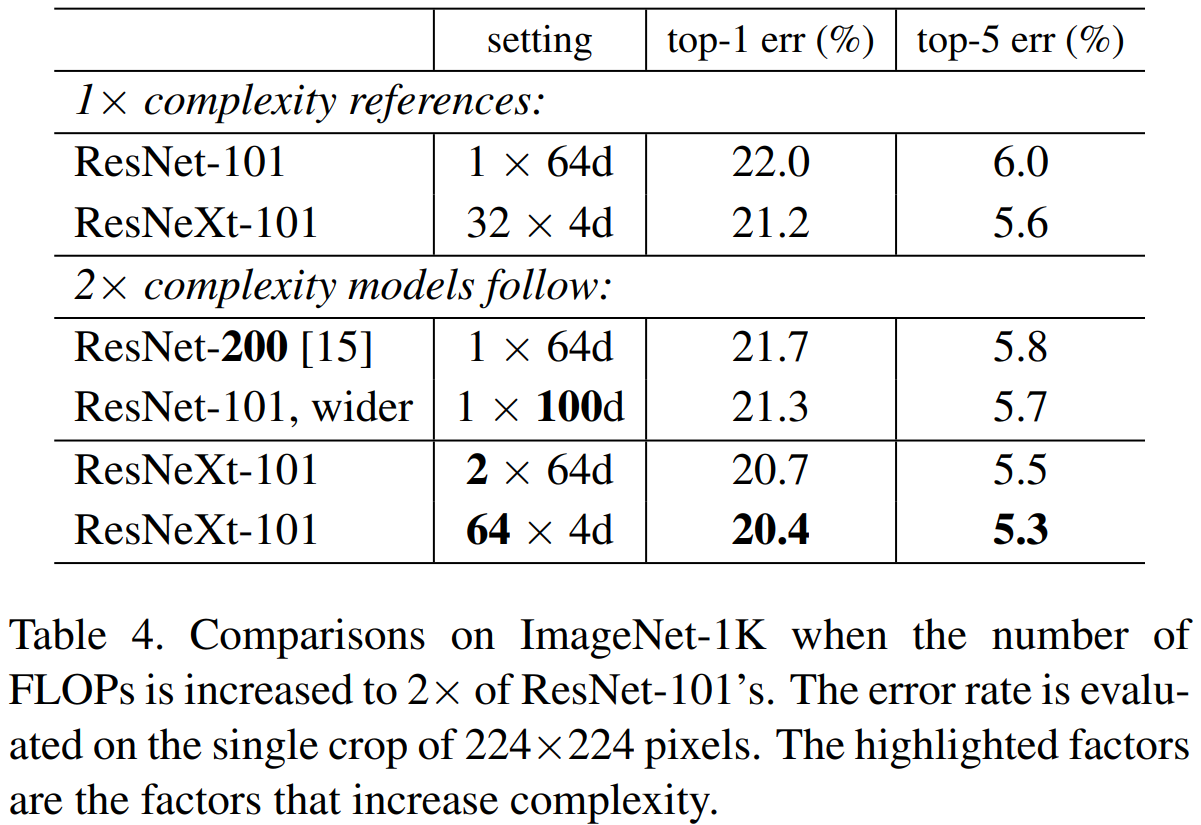
이번에는 모델의 깊이와 너비보다 cardinality가 모델의 성능에 끼치는 영향이 더 크다는 것을 검증하는 실험입니다. 먼저, ResNet101과 ResNext101($2 \times 64d$)를 비교해 보면 cardinality가 1만 더 증가했을 뿐인데도 성능이 1.3%가 향상됩니다. 그리고 동일한 ResNext101에서 cardinality를 2배로 증가 ($32 \rightarrow 64$) 시켰을 때도 성능이 0.8%가 향상됩니다.
위 두 경우는 파라미터의 개수나 FLOPs가 더 증가했기 때문에 성능 향상은 당연하다고 볼 수 있습니다. 이제 다시 복잡도가 유사한 경우를 비교해 보도록 하겠습니다. ResNet200과 ResNet101-wider를 비교해 보면 너비가 증가 ($64 \rightarrow 100$)한 것을 볼 수 있죠. 결과적으로 너비의 증가는 0.4%의 성능 향상을 얻을 수 있습니다. 하지만, ResNet200과 ResNext($2 \times 64d$)를 비교해보면 약 1.0%의 성능이 향상되어 성능 향상폭이 훨씬 더 큰 것을 볼 수 있죠. 심지어 이 상태에서 블록 내의 width는 줄이고 ($64 \rightarrow 4$) cardinality는 늘렸을 때 ($2 \rightarrow 64$) 성능이 0.3% 더 향상됩니다. 이러한 결과는 모델의 성능에는 깊이나 너비보다는 cardinality가 더 중요함을 보여주고 있죠.
3). Comparison with SOTA model
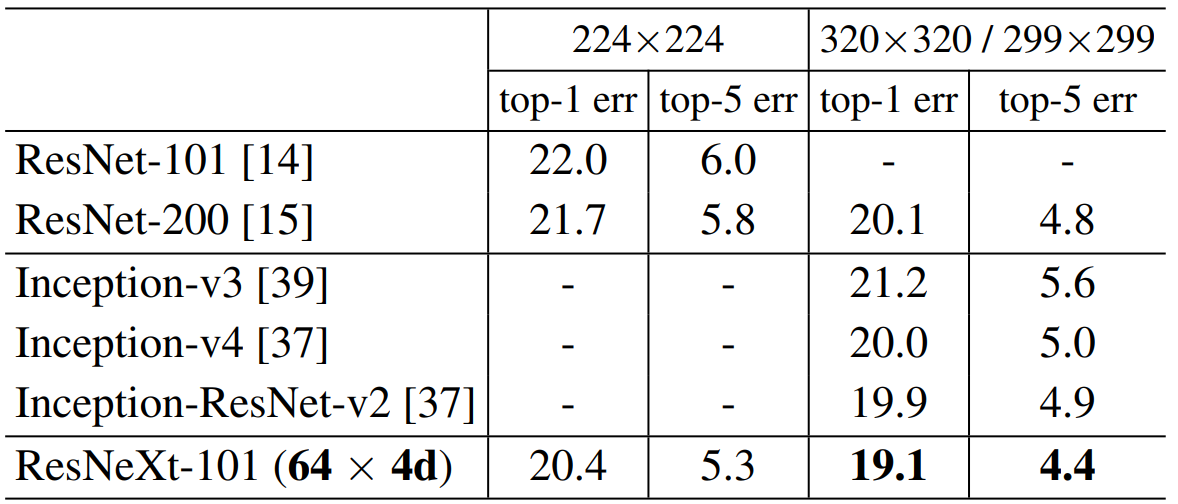
본 논문에서는 마지막으로 유명한 영상 분류 모델인 ResNet과 InceptionNet을 중심으로 성능을 비교하고 있습니다. InceptionNet-V3까지는 제가 소개했지만 InceptionNet-V4나 Inception-ResNet-V2는 아직 설명드리지 않았습니다. 이 부분은 나중에 추가적으로 리뷰를 올리도록 하겠습니다.
Implementation Code
"""resnext in pytorch
[1] Saining Xie, Ross Girshick, Piotr Dollár, Zhuowen Tu, Kaiming He.
Aggregated Residual Transformations for Deep Neural Networks
https://arxiv.org/abs/1611.05431
"""
import torch.nn as nn
import torch.nn.functional as F
#only implements ResNext bottleneck c
#"""This strategy exposes a new dimension, which we call “cardinality”
#(the size of the set of transformations), as an essential factor
#in addition to the dimensions of depth and width."""
CARDINALITY = 32
DEPTH = 4
BASEWIDTH = 64
#"""The grouped convolutional layer in Fig. 3(c) performs 32 groups
#of convolutions whose input and output channels are 4-dimensional.
#The grouped convolutional layer concatenates them as the outputs
#of the layer."""
class ResNextBottleNeckC(nn.Module):
def __init__(self, in_channels, out_channels, stride):
super().__init__()
C = CARDINALITY #How many groups a feature map was splitted into
#"""We note that the input/output width of the template is fixed as
#256-d (Fig. 3), We note that the input/output width of the template
#is fixed as 256-d (Fig. 3), and all widths are dou- bled each time
#when the feature map is subsampled (see Table 1)."""
D = int(DEPTH * out_channels / BASEWIDTH) #number of channels per group
# 4 * 64 / 64 = 4 => 32 * 4 = 128 => 1branch = 4channels
# 4 * 128 / 64 = 8 => 32 * 8 = 256 => 1branch = 8channels
# 4 * 256 / 64 = 16 => 32 * 16 = 512 => 1branch = 16channels
# 4 * 512 / 64 = 32 => 32 * 32 = 1024 => 1branch = 32channels
self.split_transforms = nn.Sequential(
nn.Conv2d(in_channels, C * D, kernel_size=1, groups=C, bias=False),
nn.BatchNorm2d(C * D), nn.ReLU(inplace=True),
nn.Conv2d(C * D, C * D, kernel_size=3, stride=stride, groups=C, padding=1, bias=False),
nn.BatchNorm2d(C * D), nn.ReLU(inplace=True),
nn.Conv2d(C * D, out_channels * 4, kernel_size=1, bias=False),
nn.BatchNorm2d(out_channels * 4),
)
self.shortcut = nn.Sequential()
if stride != 1 or in_channels != out_channels * 4:
self.shortcut = nn.Sequential(
nn.Conv2d(in_channels, out_channels * 4, stride=stride, kernel_size=1, bias=False),
nn.BatchNorm2d(out_channels * 4)
)
def forward(self, x):
return F.relu(self.split_transforms(x) + self.shortcut(x))
class ResNext(nn.Module):
def __init__(self, block, num_blocks, num_classes=100, num_channels=3):
super().__init__()
self.in_channels = 64
self.conv1 = nn.Sequential(
nn.Conv2d(num_channels, 64, 3, stride=1, padding=1, bias=False),
nn.BatchNorm2d(64),
nn.ReLU(inplace=True)
)
self.conv2 = self._make_layer(block, num_blocks[0], 64, 1)
self.conv3 = self._make_layer(block, num_blocks[1], 128, 2)
self.conv4 = self._make_layer(block, num_blocks[2], 256, 2)
self.conv5 = self._make_layer(block, num_blocks[3], 512, 2)
self.avg = nn.AdaptiveAvgPool2d((1, 1))
self.fc = nn.Linear(512 * 4, num_classes)
def forward(self, x):
x = self.conv1(x)
x = self.conv2(x)
x = self.conv3(x)
x = self.conv4(x)
x = self.conv5(x)
x = self.avg(x)
x = x.view(x.size(0), -1)
x = self.fc(x)
return x
def _make_layer(self, block, num_block, out_channels, stride):
"""Building resnext block
Args:
block: block type(default resnext bottleneck c)
num_block: number of blocks per layer
out_channels: output channels per block
stride: block stride
Returns:
a resnext layer
"""
strides = [stride] + [1] * (num_block - 1)
layers = []
for stride in strides:
layers.append(block(self.in_channels, out_channels, stride))
self.in_channels = out_channels * 4
return nn.Sequential(*layers)
def resnext50(num_classes, num_channels):
""" return a resnext50(c32x4d) network
"""
return ResNext(ResNextBottleNeckC, [3, 4, 6, 3], num_classes, num_channels)
def resnext101(num_classes, num_channels):
""" return a resnext101(c32x4d) network
"""
return ResNext(ResNextBottleNeckC, [3, 4, 23, 3], num_classes, num_channels)
def resnext152(num_classes, num_channels):
""" return a resnext152(c32x4d) network
"""
return ResNext(ResNextBottleNeckC, [3, 4, 36, 3], num_classes, num_channels)
if __name__=="__main__":
import torch
model = resnext50(num_classes=1000, num_channels=3).cuda()
inp = torch.randn(2, 3, 224, 224).cuda()
oup = model(inp)
print(oup.shape)
코드의 핵심은 ResNExtBottleNeckC 클래스를 보시면 됩니다. 이 역시 기본적으로 WRN과 마찬가지로 ResNet을 기반으로 구현되었기 때문에 전체적인 구조는 유사하고 groups 인자를 적용하기 위해 몇 가지 인자들이 추가된 것 밖에 없습니다. 보시면 CARDINALITY=32, DEPTH=4, BASEWIDTH=64로 고정되어 있는 것을 볼 수 있습니다. 위 코드는 ResNext($32 \times 4d$)를 구현한 것임을 알 수가 있죠. 여기서, BASEWIDTH는 해당 블록으로 입력되는 채널의 개수가 BASEWIDTH와 동일한 크기라면 각 branch의 grouped convolution에는 DEPTH 만큼의 채널이 할당되는 것을 의미합니다.
