안녕하세요. 지난 포스팅의 [IC2D] Rethinking the Inception Architecture for Computer Vision (CVPR2016)에서는 GoogLeNet의 발전된 모델인 InceptionNet-V2와 InceptionNet-V3에 대해서 소개시켜드렸습니다. 현재 꽤나 많이 실험 검증 단계에서 쓰이고 있는 Wide Residual Network (WRN)에 대해서 소개해드리도록 하겠습니다.
Wide Residual Networks
Deep residual networks were shown to be able to scale up to thousands of layers and still have improving performance. However, each fraction of a percent of improved accuracy costs nearly doubling the number of layers, and so training very deep residual ne
arxiv.org
Background
일단, 저희가 지금까지 보았던 영상 분류 모델은 VGGNet, GoogLeNet, ResNet, PreAct ResNet, InceptionNet 이였습니다. 이 중에서 GoogLeNet과 InceptionNet에서는 모델의 깊이도 깊이지만 한 개의 Inception Module에서 다양한 필터 크기를 적용함으로써 Multi-Scale의 관점을 도입하고자 하였습니다. 그에 반면에 VGGNet, ResNet, PreAct ResNet의 최종목표는 무조건 깊게 만들고 학습을 효율적으로 할 수 있도록 돕는 것이 목표였습니다. 일반적으로 모델이 깊어지면 2가지 문제가 발생하기 마련입니다. 첫번째는 Gradient vanishing problem으로 backward propagation 과정에서 얕은 계층으로 기울기가 전파가 되지 않는 것이고, 두번째는 Degradation problem으로 깊을수록 성능이 좋다는 직관과는 다르게 모델을 깊게 설계할 수록 성능이 떨어진다는 것 입니다. ResNet에서는 이 두가지 문제를 해결하기 위해 skip connection을 적용하였으며 실제로 성능 향상이 두드러지게 나타났습니다.
하지만, 저희가 컴퓨터 비전에서 심층 신경망을 실제로 활용하기 위해서는 복잡도를 신경안쓸수가 없습니다. 깊은 모델은 곧 메모리 및 연산량이 많아진다는 것을 의미하기 때문에 성능을 높이기 위한 단순히 깊은 모델의 설계는 큰 의미가 없어지는 것이죠. 이러한 문제는 효율적인 모델을 구성하기 위한 움직임으로 이어지게 되죠. 오늘 소개할 WRN은 깊이 (depth)는 줄이는 대신 "너비 (width)"라는 개념을 도입하여 모델을 설계합니다.
Wide Residual Networks (WRN)
본격적으로 시작하기 전에 WRN 역시 ResNet에서 파생했기 때문에 ResNet에 대한 기본 개념을 복습해보도록 하겠습니다. 일반적으로 $l$ 번째 블록의 연산은 ResNet에서 다음과 같이 정의됩니다.
$$\mathbf{x}_{l + 1} = \mathbf{x}_{l} + \mathcal{F}(\mathbf{x}_{l}, \mathcal{W}_{l})$$
여기서, $\mathbf{x}_{l}$과 $\mathbf{x}_{l + 1}$은 $l$번째 블록의 입력과 출력 특징맵입니다. $\mathcal{F}$는 Residual 블록, 그리고 $\mathcal{W}_{l}$은 $l$번째 Residual 블록의 가중치를 의미합니다.
ResNet은 깊이에 따라 두 가지 블록을 사용하여 모델을 정의합니다. 상대적으로 얕은 모델인 ResNet-18, ResNet-34에서는 Basic Block은 $3 \times 3$ 크기의 합성곱 연산을 2번 사용한 skip connection을 적용하엿죠. BottleNeck Block은 더 깊은 모델 (ResNet-50, ResNet-101 등)에서 연산량의 이점을 얻기 위해 $1 \times 1$ 합성곱을 적용하여 채널의 개수를 줄이고 $3 \times 3$ 합성곱을 적용한 뒤 다시 기존의 채널의 개수로 늘려주는 과정입니다.
한편, PreAct ResNet에서는 Identity path의 중요성과 Activation function의 순서에 따른 성능 변화를 분석하여 기존의 ResNet의 연산 순서였던 conv-bn-relu 에서 bn-relu-conv로 순서로 변경하게 됩니다.
일반적으로 Residual Block의 표현력 (representation power)을 늘리기 위해 선택할 수 있는 방법은 다음과 같습니다.
1). 블록 별로 합성곱 계층을 더 추가하기
2). 각 합성곱 계층이 더 많은 특징 맵 채널을 만들 수 있게 하기
3). 합성곱 계층의 필터 크기를 증가하기
여기서, 1)은 연산량의 이점을 잃어버리기 때문에 선택하지 않습니다. 그리고 3)은 VGGNet에서 언급했다싶이 $3 \times 3$ 크기의 합성곱을 사용하는 것이 굉장히 효율적이기 때문에 이 역시 고려대상이 아닙니다. 따라서 저희는 합성곱 계층이 더 많은 특징 맵 채널을 만들 수 있게 하면 될 거 같습니다. 여기서 말하는 채널의 개수가 곧 너비 가 됩니다.
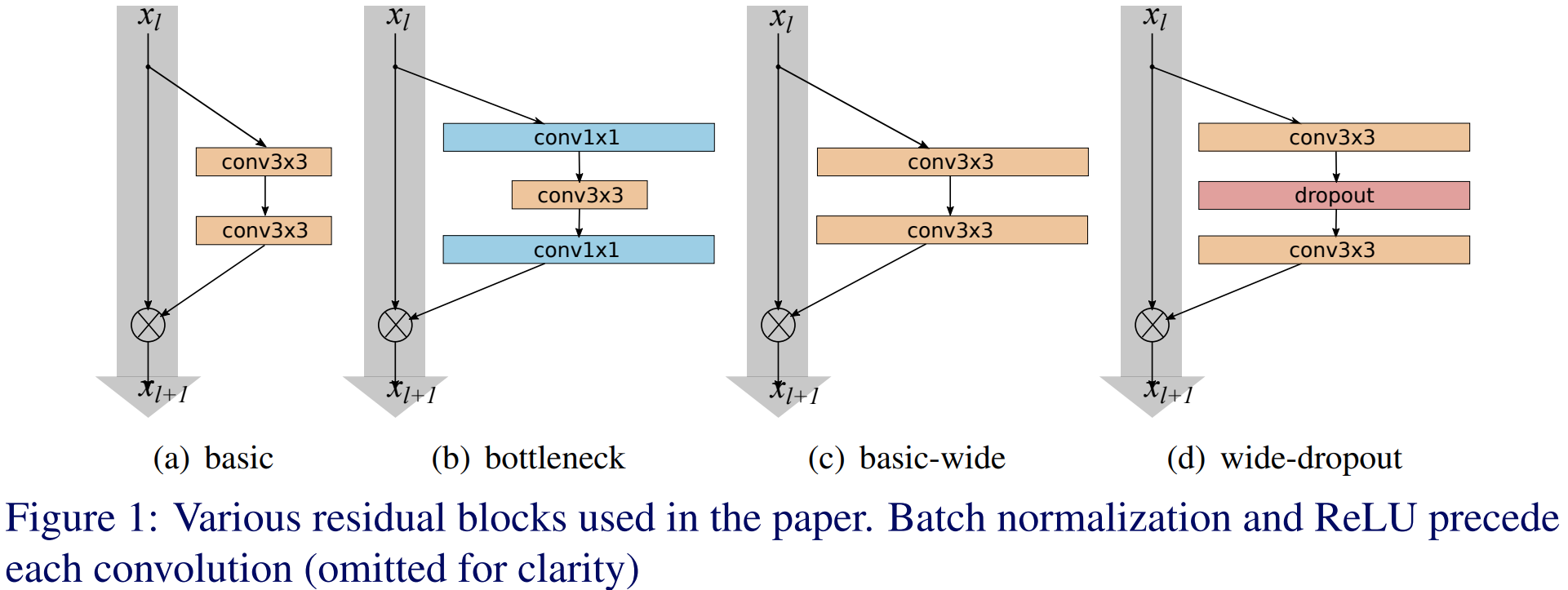
위 그림에서 (a)와 (b)가 ResNet에서 사용한 Basic Block과 BottleNeck Block입니다. (c)와 (d)는 WRN에서 정의한 새로운 블록 모양이죠. 그림을 자세히 보시면 $3 \times 3$ 크기의 합성곱 계층이 (a)와 (b)에 비해 훨씬 넓은 것을 볼 수 있습니다. 본 논문은 이 부분을 중점적으로 파고듭니다. 깊이가 아닌 각 블록에서 $3 \times 3$ 크기의 합성곱 계층의 출력 특징맵의 채널 개수를 증가시키게 되면 깊은 모델이 아니더라도 성능을 향상시킬 수 있다는 것이 본 논문의 주장이죠.
따라서, 본 논문에 따르면 WRN은 몇 가지 파라미터가 추가됩니다. 먼저, 깊이 $l$은 ResNet과 마찬가지로 모델의 깊이를 의미합니다. 너비 $k$는 기존의 Basic Block의 $3 \times 3$ 크기의 합성곱 계층의 출력 특징맵의 채널 개수에 곱하는 요소로 $k$가 클수록 더욱 넓은 모델이 되는 것입니다.
이제 블록의 형태를 결정하는 방법을 알았으니 한 가지 새로운 기호를 도입해보도록 하겠습니다. $B(M)$은 residual block의 구조를 의미합니다. 여기서 $M$은 해당 블록에서 사용된 합성곱 계층의 필터 크기를 의미하죠. 예를 들어 $B(3, 1)$은 $3 \times 3$ 크기의 합성곱과 $1 \times 1$ 크기의 합성곱을 Residual Block에서 사용했음을 의미하죠. 본 논문에서는 이 기호를 이용해서 다양한 조합의 필터 크기에 대한 실험을 진행합니다. 실험하는 블록은 다음과 같습니다.
1). $B(3, 3)$ : Residual Block의 Basic Block
2). $B(3, 1, 3)$ : Residual Block의 Basic Block에서 가운데 $1 \times 1$ 합성곱 계층 추가
3). $B(1, 3, 1)$ : Residual Block의 BottleNeck Block
4). $B(1, 3)$ : $1 \times 1$ 합성곱 적용 후 $3 \times 3$ 합성곱 적용
5). $B(3, 1)$ : $3 \times 3$ 합성곱 적용 후 $1 \times 1$ 합성곱 적용
6). $B(3, 1, 1)$ : Network-In-Network 스타일의 구조
위 기호를 사용해 본 논문에서 제안하는 모델을 설명하면 WRN-40-2-$B(3, 3)$과 같이 표시할 수 있습니다. 이는 Wide Residual Network를 사용할 때 깊이 $l = 40$, 너비 $k = 2$ 그리고 해당 블록은 $B(3, 3)$으로 기존의 Residual Block을 사용했다는 것을 의미합니다.
Experiment Results
1). Types of Convolutions in Residual Block
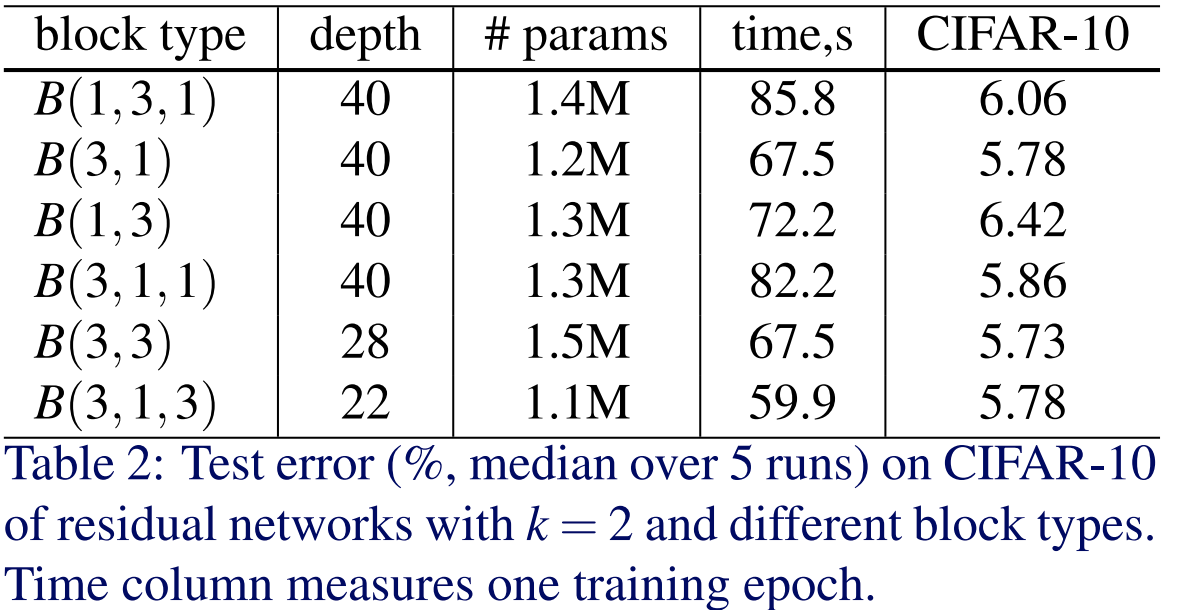
본 논문에서는 먼저 모델의 블록 모양 $B(M)$ 실험을 CIFAR10과 CIFAR100에 대해서 진행합니다. 여기서, time은 에폭별 학습 시간을 초 단위로 표시한 것 입니다. 이때 유의할 점은 깊이가 조금씩 다르다는 점 입니다. 블록 종류별로 파라미터의 개수가 다르기 때문에 본 논문에서는 파라미터의 개수에 따른 성능 변화를 억제하기 위해 위와 같이 깊이를 조절하면서 전체 파라미터의 개수를 맞추어 실험을 한 모습입니다. 실험 결과는 기본적으로 WRN-28-2-$B(3, 3)$이 WRN-22-2-$B(3, 1, 3)$에 비해서 아주 살짝 성능이 향상 (0.05%)된 것을 볼 수 있습니다.
2). Number of Convolutions per Block

본 논문에서는 다음으로 블록별로 합성곱 계층의 개수를 다르게 하면서 실험을 진행하였습니다. 이때, 사용한 네트워크는 WRN-40-2를 기본으로 사용하였으며 $B(3), B(3, 3), B(3, 3, 3), B(3, 3, 3, 3)$ 간의 성능 비교를 하였습니다. 실험 결과는 1개의 계층만을 사용했을 때 성능이 제일 좋지 않았습니다. 2개의 계층을 사용했을 때 최고의 성능이 나왔기 때문에 본 논문에서는 이후 실험에서 $B(3, 3)$으로 고정하여 실험을 진행하였습ㄴ디ㅏ.
1) ~ 2)의 실험은 기본적으로 여러 가지의 종류의 블록 중 어떤 종류를 사용하는 것이 합리적인지에 대한 실험을 진행한 것 입니다.
3). Width of Residual Blocks
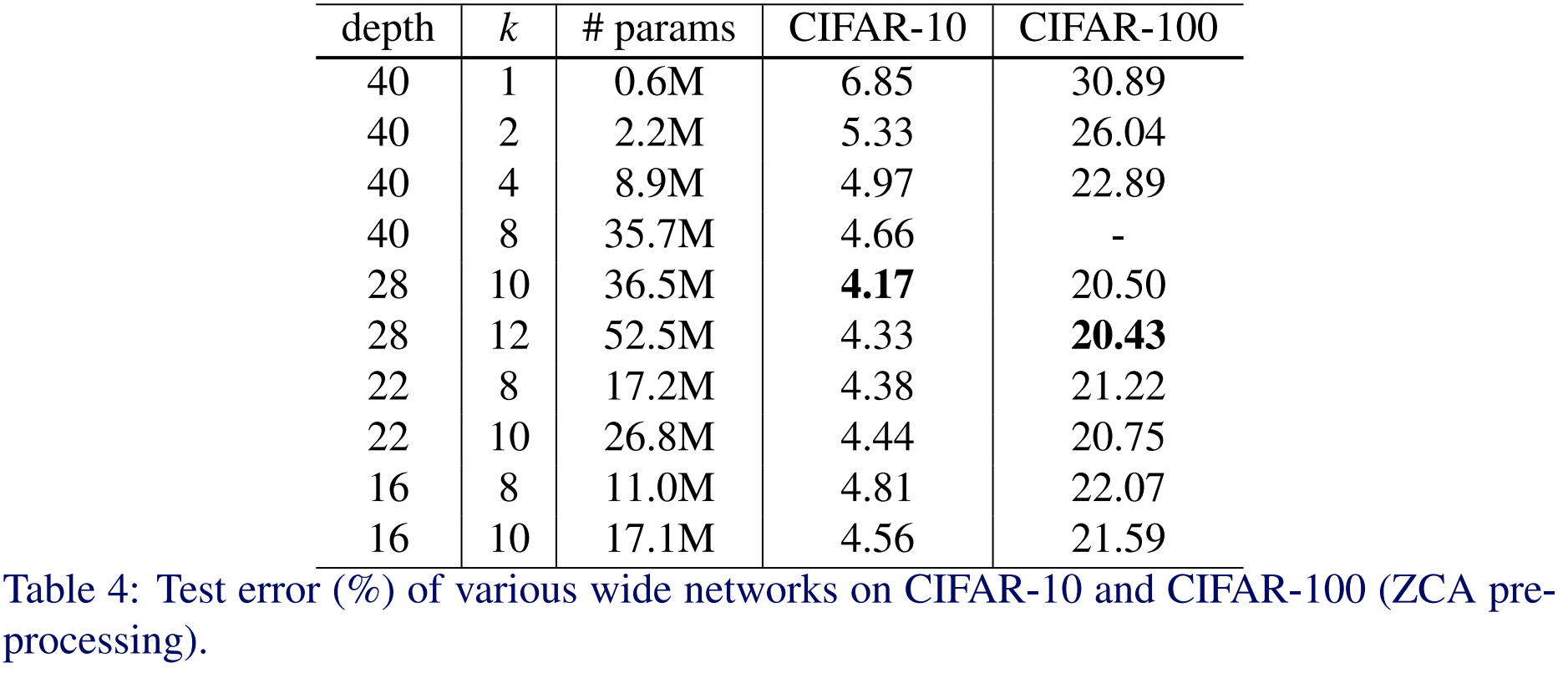
다음으로 본 논문에서는 Widening Factor $k$와 Depth $l$에 대한 성능 변화를 측정하였습니다. 여기서 $k = 1$이라면 기존의 ResNet과 동일한 구조 입니다. 일단, $l = 40$으로 고정하고 성능을 비교해보면 $k$가 증가함에 따라 성능이 일관되게 향상되고 있는 것을 볼 수 있습니다. 실제로 기존의 ResNet과 비교해보면 $WRN-40-8$과 약2.19%의 성능 차이가 발생하는 것을 볼수가 있죠. 다음으로 $k = 10$으로 고정하고 WRN-28-10, WRN-22-10, WRN-16-10을 비교해보면 일반적으로 저희가 생각한 것과 같이 깊어질수록 성능이 좋아지는 것을 볼 수가 있죠. 마지막으로 유사한 파라미터를 가지는 WRN-28-10 그리고 WRN-40-8과 비교해보면 깊이가 깊지 않음에도 Widening Factor $k$를 증가시킴으로써 충분히 좋은 성능을 낼 수 있다는 것을 실험적으로 검증하고 있습니다.
4). Comparison between Other Models
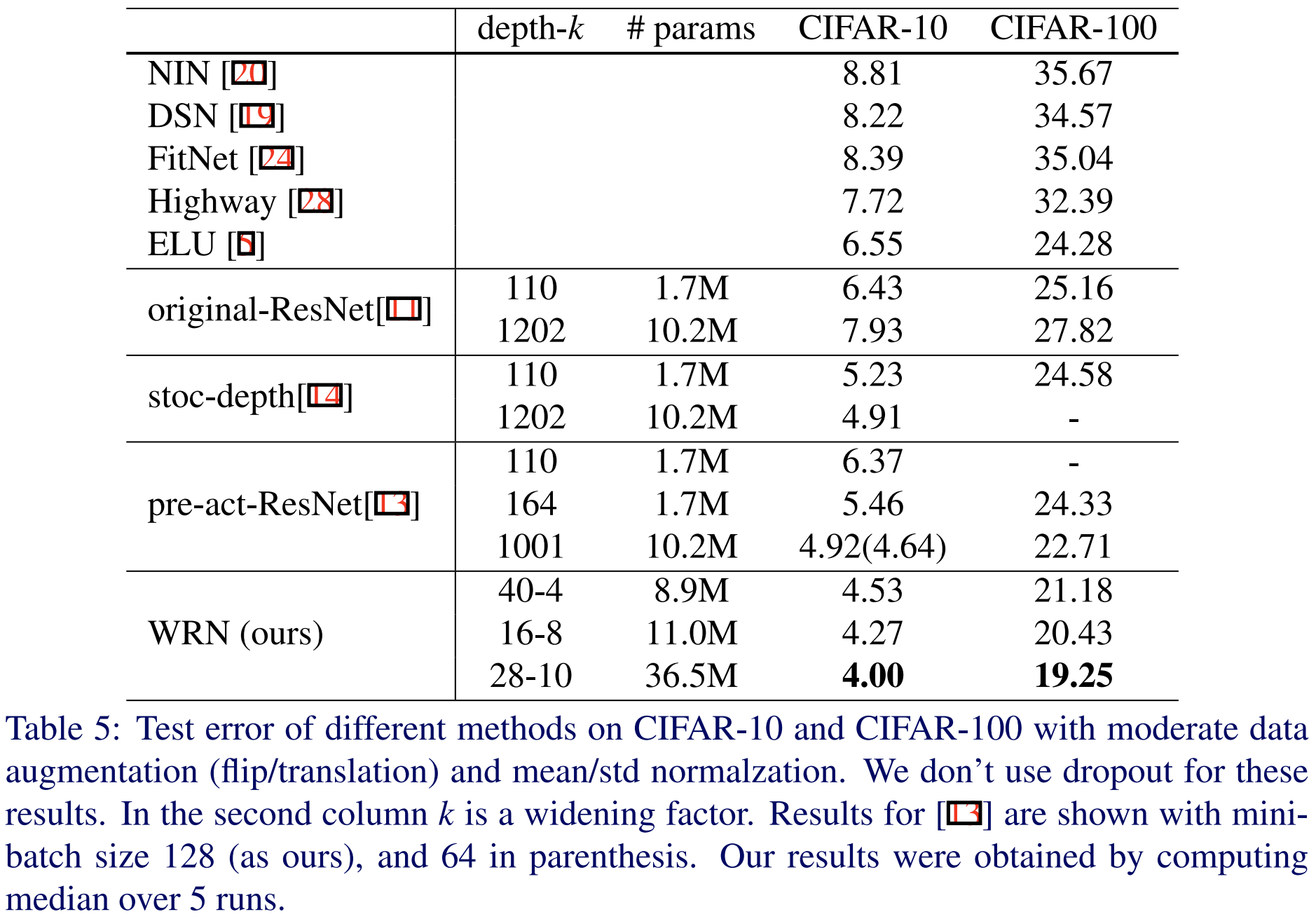
이제 다른 영상 분류 모델들과 비교해보도록 하겠습니다. 본 논문에서는 ResNet, Stochastic Depth ResNet, PreAct ResNet과 성능을 비교하였습니다. 놀라운 점은 ResNet-1202, Stochastic Depth ResNet-1202, PreAct ResNet-1001과 비교했을 때 깊이는 낮추고 너비만 늘렷을 때 훨씬 높은 성능을 얻을 수 있다는 점 입니다. 이러한 실험은 심층 신경망을 설계할 때 너비에 대한 중요도가 생각보다 높음을 의미하죠.
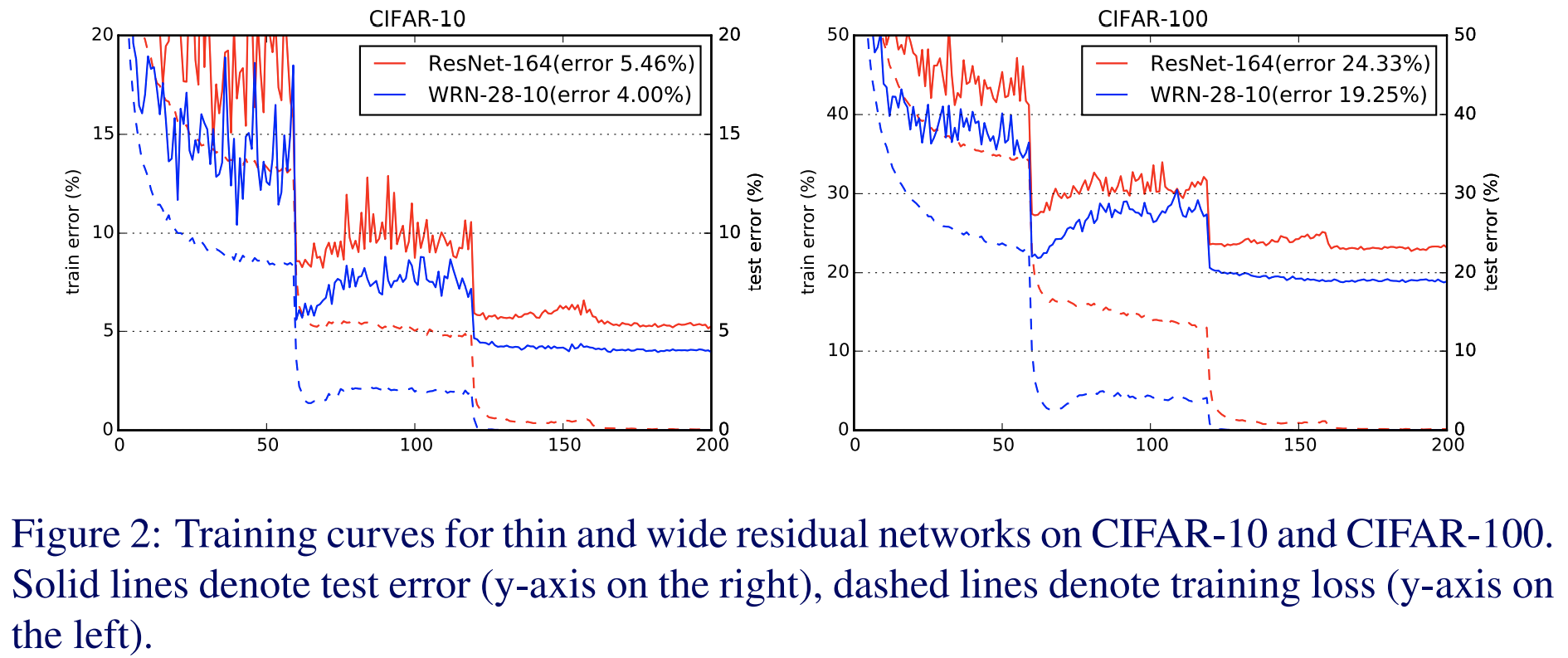
위 그림은 ResNet과 WRN 사이의 에폭에 따른 손실함수 경향성을 비교하고 있습니다. 일반적으로 과적합을 막으려면 시험 손실함수과 훈련 손실함수의 차이가 적어야하죠. 그런 관점에서 WRN은 ResNet보다 두 차이가 적기 때문에 과적합이 방지되고 있음을 알 수 있습니다.
5). Dropout in Residual Blocks
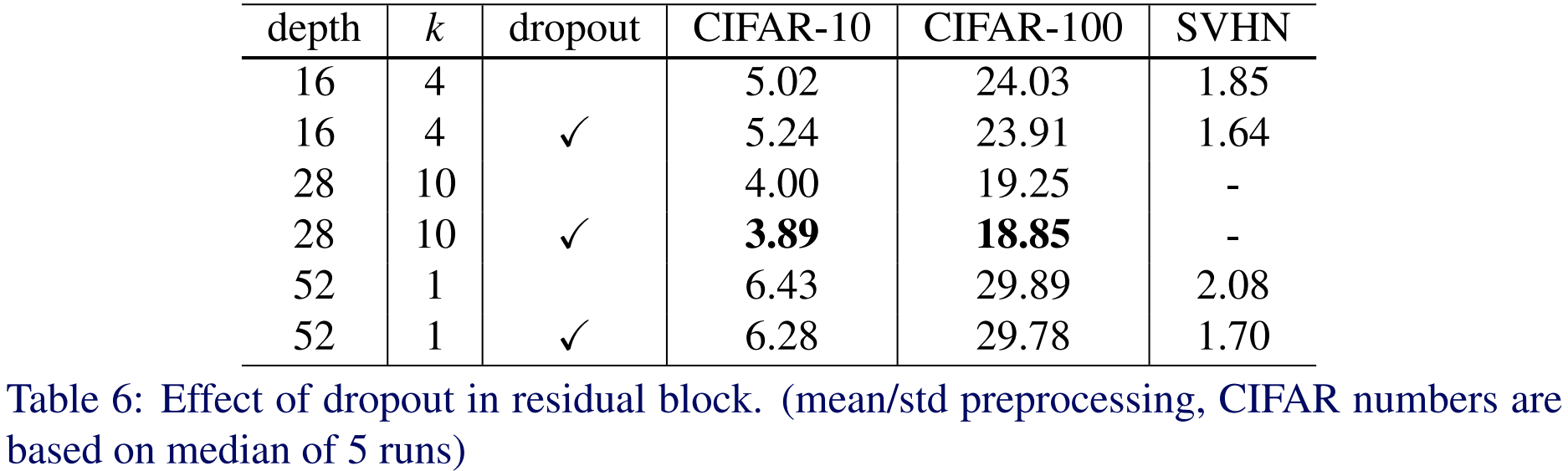
마지막으로 Dropout을 추가했을 때 성능 변화를 실험합니다. Dropout은 모델의 깊이가 상대적으로 깊을 때 더 높은 성능 향상을 얻을 수 있다는 것을 볼 수 있습니다.
6). ImageNet Classification
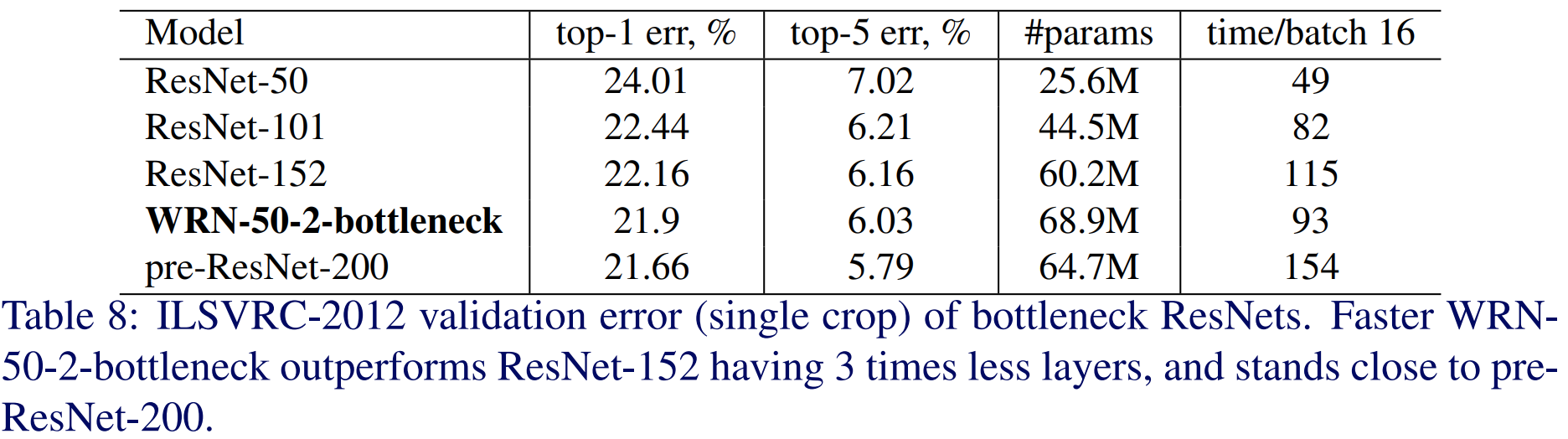
마지막으로 ImageNet에 적용하여 실험을 했을 PreAct ResNet보다는 살짝 낮은 성능이지만 더 얕은 깊이로 거의 유사한 성능을 냈다는 점에서 효율적인 모델이라는 것을 검증합니다.
Code Implementation
import torch
import torch.nn as nn
class WideBasic(nn.Module):
def __init__(self, in_channels, out_channels, stride=1):
super().__init__()
self.residual = nn.Sequential(
nn.BatchNorm2d(in_channels),
nn.ReLU(inplace=True),
nn.Conv2d(
in_channels,
out_channels,
kernel_size=3,
stride=stride,
padding=1
),
nn.BatchNorm2d(out_channels),
nn.ReLU(inplace=True),
nn.Dropout(),
nn.Conv2d(
out_channels,
out_channels,
kernel_size=3,
stride=1,
padding=1
)
)
self.shortcut = nn.Sequential()
if in_channels != out_channels or stride != 1:
self.shortcut = nn.Sequential(
nn.Conv2d(in_channels, out_channels, 1, stride=stride)
)
def forward(self, x):
residual = self.residual(x)
shortcut = self.shortcut(x)
return residual + shortcut
class WideResNet(nn.Module):
def __init__(self, num_classes, num_channels, block, depth=50, widen_factor=1):
super().__init__()
self.depth = depth
k = widen_factor
l = int((depth - 4) / 6)
self.in_channels = 16
self.init_conv = nn.Conv2d(num_channels, self.in_channels, 3, 1, padding=1)
self.conv2 = self._make_layer(block, 16 * k, l, 1)
self.conv3 = self._make_layer(block, 32 * k, l, 2)
self.conv4 = self._make_layer(block, 64 * k, l, 2)
self.bn = nn.BatchNorm2d(64 * k)
self.relu = nn.ReLU(inplace=True)
self.avg_pool = nn.AdaptiveAvgPool2d((1, 1))
self.linear = nn.Linear(64 * k, num_classes)
def forward(self, x):
x = self.init_conv(x)
x = self.conv2(x)
x = self.conv3(x)
x = self.conv4(x)
x = self.bn(x)
x = self.relu(x)
x = self.avg_pool(x)
x = x.view(x.size(0), -1)
x = self.linear(x)
return x
def _make_layer(self, block, out_channels, num_blocks, stride):
"""make resnet layers(by layer i didnt mean this 'layer' was the
same as a neuron netowork layer, ex. conv layer), one layer may
contain more than one residual block
Args:
block: block type, basic block or bottle neck block
out_channels: output depth channel number of this layer
num_blocks: how many blocks per layer
stride: the stride of the first block of this layer
Return:
return a resnet layer
"""
# we have num_block blocks per layer, the first block
# could be 1 or 2, other blocks would always be 1
strides = [stride] + [1] * (num_blocks - 1)
layers = []
for stride in strides:
layers.append(block(self.in_channels, out_channels, stride))
self.in_channels = out_channels
return nn.Sequential(*layers)
# Table 9: Best WRN performance over various datasets, single run results.
def WRN(num_classes, num_channels, depth=28, widen_factor=10):
net = WideResNet(num_classes, num_channels, WideBasic, depth=depth, widen_factor=widen_factor)
return net기본적으로 WRN 역시 ResNet 기반의 모델이기 때문에 크게 다르지 않습니다. 설명할 때는 길게 설명했지만 핵심은 기존 Basic Block에서 채널의 개수를 얼마나 늘려줄지에 대한 Widening factor $k$만 넣어주면 되는 것이죠. 이때, Basic Block은 PreAct ResNet과 동일하게 작성합니다.
위 코드에서 WideResNet 클래스의 인자 중에 widen_factor가 보이실 겁니다. 저희는 이 인자를 이용해서 조절할 수 있죠. 이때, _make_layer 함수를 이용해서 블록을 구성할 때 기존에 넘겨주던 채널의 개수에 $k$를 곱해주면 모든 구현은 끝납니다.
