안녕하세요. 지난 포스팅의 [IC2D] Deep Residual Learning for Image Recognition (CVPR2016)에서는 ResNet 계열 모델의 시작을 알린 ResNet에 대해서 소개해드렸습니다. 오늘은 이 ResNet을 좀 더 심층적으로 분석하고 좀 더 성능을 향상시킬 수 있는 방법에 대해 소개한 논문에 대해서 소개해드리고자 합니다. 이를 통해 새로운 형태의 ResNet을 PreAct ResNet이라고 정의합니다. 본 논문에서는 어떤 방식으로 해당 모델을 정의하게 됬는지 한번 알아보도록 하죠.
Identity Mappings in Deep Residual Networks
Deep residual networks have emerged as a family of extremely deep architectures showing compelling accuracy and nice convergence behaviors. In this paper, we analyze the propagation formulations behind the residual building blocks, which suggest that the f
arxiv.org
배경
기본적으로 Residual Network는 기존의 VGG와 GoogLeNet과 비교했을 때 굉장히 좋은 성능을 보일뿐만 아니라 손실함수의 수렴 역시 안정적으로 흘러갔습니다. 특히, 중요한 것은 일반적으로 저희가 생각했을 때 깊이는 성능에 비례한다는 원칙에 위배되는 Degradation Problem을 해결하였죠. 하지만, 이러한 ResNet에 대해서 몇 가지 의문점이 발생하게 됩니다.
1). Identity Mapping에 비선형성 계층 추가 시 발생되는 성능 변화
2). Residual Block 내에서 활성화 함수의 순서의 영향
오늘 논문은 이렇게 2가지 관점에서 ResNet을 분석하고자 합니다.
사전 지식
본격적으로 ResNet을 분석하기 이전에 ResNet의 기본적인 특성을 이해해야합니다. 기존 논문에 따르면 1개의 Residual Block은 다음과 같이 함수처럼 쓸 수 있습니다.
$$\begin{align*} \mathbf{y}_{l} &= h(\mathbf{x}_{l}) + \mathcal{F}(\mathbf{x}_{l}, \mathcal{W}_{l}) \\ \mathbf{x}_{l + 1} &= f(\mathbf{y}_{l}) \end{align*}$$
여기서, $\mathbf{x}_{l}$은 $l$번째 Residual Block을 의미합니다. 그리고 $\mathcal{W}_{l} = \{W_{l, k} | 1 \le k \le K\}$은 $l$번째 Residual Block에 해당하는 모든 가중치의 집합입니다. 이때, $K$는 1개의 Residual Block 안에 포함된 합성곱 계층의 개수로 지난 논문에 따르면 ResNet-18과 ResNet-34에서는 $K = 2$이고 $ResNet-50, ResNet-101$에서는 $K = 3$이였습니다. $\mathcal{F}$는 Residual Block이고 $f$는 Identity Mapping과 Residual Block 사이의 원소별 덧셈을 한 뒤 수행되는 활성화 함수로 지난 논문에서는 ReLU 활성화 함수를 사용하였습니다. 그리고 $h$는 항등함수로 $h(\mathbf{x}_{l}) = \mathbf{x}_{l}$이였죠.
이제, $f$ 역시 $h$와 마찬가지로 항등함수라고 가정하면 $f(\mathbf{y}_{l}) = \mathbf{y}_{l} = \mathbf{x}_{l + 1}$이므로 다음과 같이 쓸 수 있습니다.
$$\mathbf{x}_{l + 1} = x_{l} + \mathcal{F}(\mathbf{x}_{l}, \mathcal{W}_{l})$$
이 식을 재귀적으로 써서 $L$번째 Residual Block의 출력을 다음과 같이 쓸 수 있습니다.
$$\begin{align*} \mathbf{x}_{L} &= \mathbf{x}_{L - 1} + \mathcal{F}(\mathbf{x}_{L - 1}, \mathcal{W}_{L - 1}) \\ &= \left( \mathbf{x}_{L - 2} + \mathcal{F}(\mathbf{x}_{L - 2}, \mathcal{W}_{L - 2}) \right) + \mathcal{F}(\mathbf{x}_{L - 1}, \mathcal{W}_{L - 2}) = \mathbf{x}_{L - 2} + \sum_{i = L - 2}^{L - 1} \mathcal{F}(\mathbf{x}_{i}, \mathcal{W}_{i}) \\ &= \cdots \\ &= \mathbf{x}_{0} + \sum_{i = 1}^{L - 1} \mathcal{F}(\mathbf{x}_{i}, \mathcal{W}_{i}) \end{align*}$$
이 결과는 저희에게 2가지 사실을 알려줍니다.
1). $L$번째 Residual Block인 $\mathbf{x}_{L}$은 임의의 얕은 $l$번째 입력 $\mathbf{x}_{l}$과 Residual Function의 합으로 표현할 수 있다.
2). $L$번째 Residual Block인 $\mathbf{x}_{L}$은 모든 Residual Function 출력의 합이다.
이와 같은 사실은 활성화함수의 존재를 무시하면 $\Pi_{i = 0}^{L - 1} W_{i}\mathbf{x}_{0}$과 같이 쓸 수 있는 기존의 Plain network (VGGNet 등)과는 다른 결과로 $W_{i}$가 매우 작거나 커지면 입력값이 소실되는 문제가 발생하는 것을 볼 수 있습니다. 하지만, ResNet에서는 어떠한 계층에서도 얕은 계층에서 추가정보를 받을 수 있기 때문에 입력값 정보가 보존되는 것이죠.
이번에는 $\mathbf{x}_{l}$에 대해서 손실함수 $\epsilon$을 미분해보도록 하겠습니다. 미적분학의 사슬법칙만 적용하면 쉽게 풀 수 있습니다.
$$\frac{\partial \epsilon}{\partial \mathbf{x}_{l}} = \frac{\partial \epsilon}{\partial \mathbf{x}_{L}} \frac{\partial \mathbf{x}_{L}}{\partial \mathbf{x}_{l}} = \frac{\partial \epsilon}{\partial \mathbf{x}_{L}} \left( 1 + \frac{\partial}{\partial \mathbf{x}_{l}} \sum_{i = 1}^{L - 1} \mathcal{F}(\mathbf{x}_{i}, \mathcal{W}_{i}) \right)$$
결과적으로 저희는 $\mathbf{x}_{l}$에 대해서 손실함수 $\epsilon$을 미분인 $\frac{\partial \epsilon}{\partial \mathbf{x}_{l}}$을 두 개의 항으로 분해할 수 있습니다.
1). $\frac{\partial \epsilon}{\partial \mathbf{x}_{L}}$ : 임의의 깊이에 있는 계층 $\mathbf{x}_{L}$에 대한 손실함수의 미분을 임의의 얕은 계층으로 전달가능하기 때문에 기울기 소실 및 폭발 현상이 해결
2). $\frac{\partial \epsilon}{\partial \mathbf{x}_{L}} \left( \frac{\partial}{\partial \mathbf{x}_{l}} \sum_{i = 1}^{L - 1} \mathcal{F}(\mathbf{x}_{i}, \mathcal{W}_{i}) \right)$ : 가중치 계층의 기울기로 일반적으로 $\frac{\partial}{\partial \mathbf{x}_{l}} \sum_{i = 1}^{L - 1} \mathcal{F}(\mathbf{x}_{i}, \mathcal{W}_{i}) \neq 1$이므로 기울기 소실 문제 해결
이러한 이유로 ResNet은 기존의 Plain Network에 비해 학습이 안정적이고 높은 성능이 있다는 것을 알게 되었습니다. 이제부터는 본격적으로 ResNet의 변형된 구조를 통해 Identity Mapping의 중요성과 활성화 함수의 순서가 미치는 성능 변화를 분석해보도록 하겠습니다.
Identity Skip Connection의 중요성

이번 절에서는 위 그림과 같이 Skip Connection $h$을 다양하게 변형하여 성능을 분석합니다. 총 6가지의 변형을 만들었으며 가장 먼저, Constant Scaling에 대한 설명을 해보도록 하겠습니다.
Constant Scaling
Constant Scaling이란 이름에서도 보이는 것처럼 $h$가 어떤 상수값을 곱하는 것을 의미합니다. 즉, $h(\mathbf{x}_{l}) = \lambda_{l} \mathbf{x}_{l}$이라고 쓸 수 있습니다. 따라서, $\mathbf{x}_{l + 1} = \lambda_{l}\mathbf{x}_{l} + \mathbf{F}(\mathbf{x}_{l}, \mathcal{W}_{l})$로 쓸 수 있습니다. 이 식을 저희가 아까 분석했던 결과에 대입하면 아래와 같이 변합니다.
$$\begin{cases} &\mathbf{x}_{L} = \left( \Pi_{i = l}^{L - 1} \lambda_{i} \right)\mathbf{x}_{l} + \sum_{i = 1}^{L - 1} \left( \Pi_{j = i + 1}^{L - 1} \lambda_{j} \right) \mathcal{F}(\mathbf{x}_{i}, \mathcal{W}_{i}) \\ &\frac{\partial \epsilon}{\partial \mathbf{x}_{l}} = \frac{\partial \epsilon}{\partial \mathbf{x}_{L}} \left( \left( \Pi_{i = 1}^{L - 1} \lambda_{i} \right) + \frac{\partial}{\partial \mathbf{x_{l}}} \sum_{i = 1}^{L - 1} \left( \Pi_{j = i + 1}^{L - 1} \right) \mathcal{F}(\mathbf{x}_{i}, \mathcal{W}_{i})\right) \end{cases}$$
해당 식에서 핵심은 $\Pi_{i = 1}^{L - 1} \lambda_{i}$입니다. 만약, $L$이 굉장히 깊은 계층으로 $L = 1000$ 이라고 가정하고 $\lambda_{i}$가 모든 계층에 대해서 1보다 작다면 gradient가 없어지게 됩니다. 따라서, 기울기 소실문제가 발생하겠죠. 반대로 1보다 크면 gradient가 폭팔하기 때문에 기울기 폭팔 문제가 발생할 것 입니다. 이와 같은 이유로 Constant Scaling은 실험도 하기 전에 학습이 굉장히 어려울 것으로 예상할 수 있죠.

실제로 그림 (b)와 같이 학습하면 최적화가 안되는 것을 볼 수 있습니다. 실제로 shortcut에는 0.5 그리고 Residual Block에서는 0.5 만큼 비율을 할당해서 학습했을 때 성능이 크게 감소한 것을 볼 수 있죠.
Exclusive Gating
몇몇 논문에서는 데이터와 기울기의 흐름을 조절하기 위해 Block 뒤에 Gate 함수를 정의하여 사용하기도 합니다. 대표적으로 LSTM이 있죠. 이번에는 Gating function $g(\mathbf{x}) = \sigma(W_{g}\mathbf{x} + b_{g})$를 사용하여 학습을 진행해보도록 하겠습니다. 여기서, $\sigma$는 시그모이드 함수를 의미합니다. 그리고 이를 shortcut path와 Residual path에 둘 다 정의하여 학습하였죠.

실험적으로는 역시 original 보다도 성능이 낮은 것을 관찰할 수 있습니다. 다만, 한 가지 사실은 exclusive gating을 통해 학습할 때는 $b_{g}$의 초기화값이 지대한 영향을 끼친다는 사실입니다. 그런데 여기서 놀라운 결과는 학습 결과 $g(\mathbf{x})$가 거의 0으로 수렴했다는 점 입니다. 이는 shortcut path가 gating 없이 그대로 통과하는 것이 더 중요하다는 사실을 뒷받침해주고 있죠. 하지만, $g(\mathbf{x})$가 0으로 수렴했기 때문에 residual path의 영향력이 감소하여 성능이 감소한 것으로 해석할 수 있습니다.
Shortcut-only Gating
바로 직전의 실험결과로 저자들은 Shortcut에만 gating function을 도입해보기로 결정합니다.

이번에도 마찬가지로 $b_{g}$의 영향이 굉장히 크다는 것을 알 수 있습니다. 여기서 한 가지 재밌는 사실은 또 다시 $1 - g(\mathbf{x})$가 거의 1으로 수렴했다는 점 입니다. 이는 shortcut path가 gating 없이 그대로 통과하는 것이 더 중요하다는 사실을 한번 더 강조합니다. 그리고 Residual path의 영향도 그대로기 때문에 실질적으로 original과 가장 유사한 결과를 얻을 수 있습니다.
$1 \times 1$ 합성곱 계층을 추가한 Shortcut과 DropOut을 추가한 Shortcut
일반적으로 비선형성과 DropOut을 추가하면 성능이 오르는 것으로 알고 있습니다. 본 논문에서는 마지막으로 Shortcut에 $1 \times 1$ 합성곱 계층과 DropOut을 추가하여 학습을 해보죠.

실험 결과는 오히려 성능 감소가 훨씬 컸다는 것을 알 수 있습니다.

뿐만 아니라 모든 경우에 Shortcut path를 건들이면 성능이 감소하고 학습이 어려워 진다는 점을 강조합니다. 즉, Residual Network에서는 Shortcut path를 최대한 건들이지 않는 것이 중요한 것을 알 수 있습니다.
활성화 함수의 변형

이번에는 위 그림과 같이 Residual Block 내에서 활성화 함수의 위치를 다양하게 바꾸어가며 성능을 측정하였습니다.
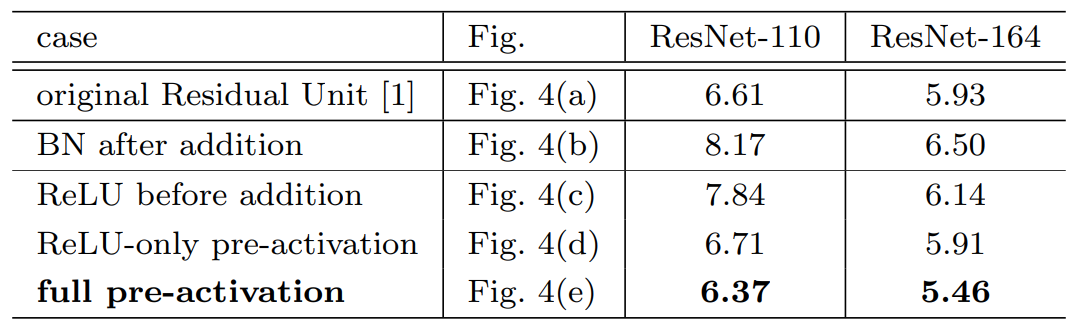
실험 결과를 분석해보면 그림 (b)와 같이 더한 뒤 바로 배치 정규화 (BN)를 적용했을 때 성능 하락폭이 가장 큰 것을 볼 수 있습니다. 이러한 결과는 다시 배치 정규화가 shortcut 에 포함되기 때문에 성능이 감소한 것으로 해석할 수 있습니다. 다음으로 Residual path 상에서 배치정규화를 적용한 뒤 ReLU를 적용하게 되면 성능 하락이 되는 것을 볼 수 있습니다. 이러한 결과는 Residual path의 출력이 $[0, \infty)$로 제한되어 shortcut path와의 range가 안맞기 때문입니다. 다음으로 배치 정규화와 ReLU를 Residual path의 가장 앞으로 옮겨보면 가장 높은 성능을 달성하게 됩니다. 즉, 기존에는 활성화 함수들을 뒤에 배치했기 때문에 Post Activation model이라고 부를 수 있고, 이번에는 앞에 배치했기 때문에 Pre Activation model이라고 부릅니다. 따라서, 이와 같은 구조의 ResNet을 PreAct ResNet이라고 하게 되는 것이죠.
실험 결과

실험은 주로 PostAct ResNet과 비교하게 됩니다. 어느정도 깊게 쌓게 되면 PostAct ResNet은 성능이 오히려 떨어지지만 PreAct ResNet은 성능이 깊이에 따라서 더 향상되는 것을 볼 수 있습니다.
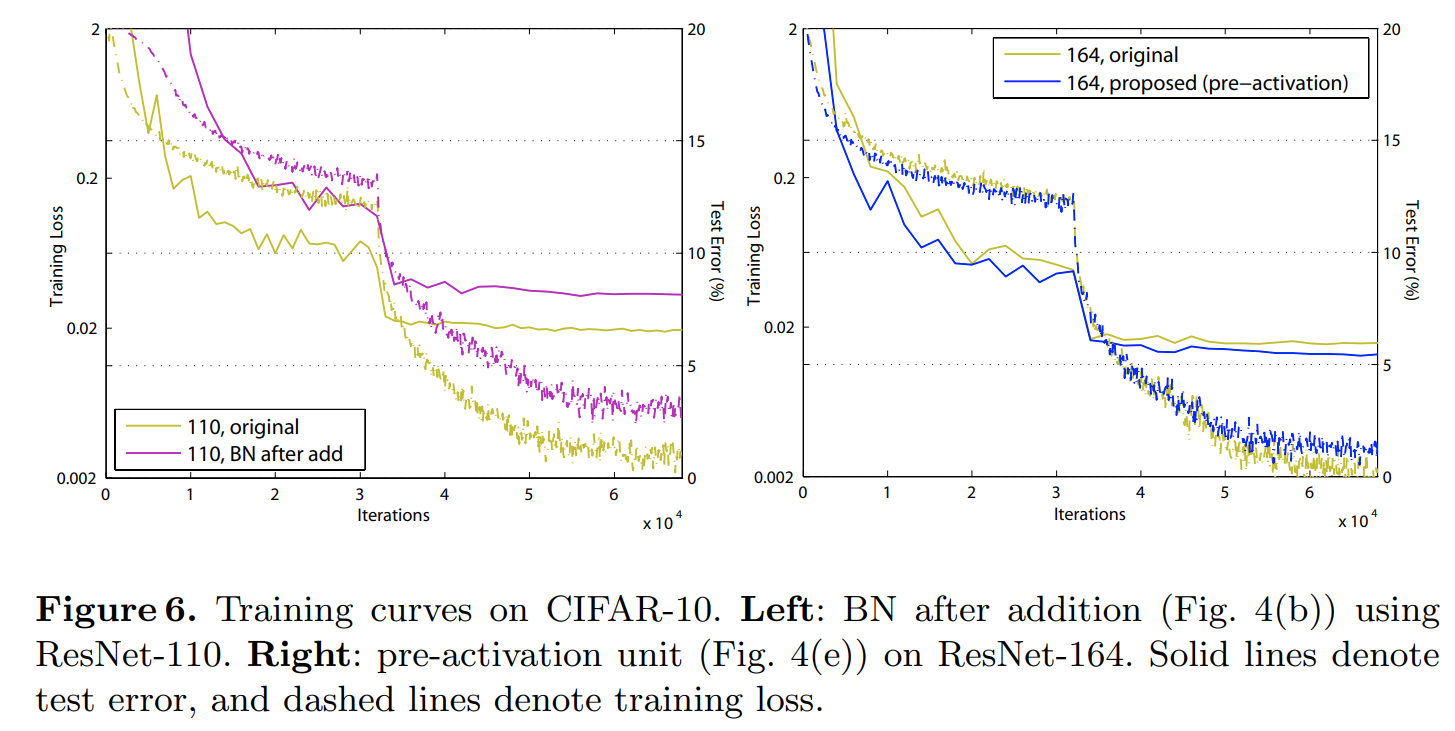
뿐만 아니라, 학습의 안정성 및 수렴 속도도 향상된 것을 볼 수 있죠. 이러한 결과는 더욱 깊은 모델에서 최적화가 쉬워지고 과적합 현상을 줄일 수 있기 때문에 얻을 수 있습니다.
class BottleNeck(nn.Module):
"""Residual block for resnet over 50 layers
"""
expansion = 4
def __init__(self, in_channels, out_channels, stride=1):
super().__init__()
self.residual_function = nn.Sequential(
nn.BatchNorm2d(in_channels), nn.ReLU(inplace=True),
nn.Conv2d(in_channels, out_channels, kernel_size=1, bias=False),
nn.BatchNorm2d(out_channels), nn.ReLU(inplace=True),
nn.Conv2d(out_channels, out_channels, stride=stride, kernel_size=3, padding=1, bias=False),
nn.BatchNorm2d(out_channels), nn.ReLU(inplace=True),
nn.Conv2d(out_channels, out_channels * BottleNeck.expansion, kernel_size=1, bias=False),
)
self.shortcut = nn.Sequential()
if stride != 1 or in_channels != out_channels * BottleNeck.expansion:
self.shortcut = nn.Sequential(
nn.Conv2d(in_channels, out_channels * BottleNeck.expansion, stride=stride, kernel_size=1, bias=False),
nn.BatchNorm2d(out_channels * BottleNeck.expansion)
)
def forward(self, x):
return self.residual_function(x) + self.shortcut(x)
class BasicBlock(nn.Module) :
"""Basic Block for resnet 18 and resnet 34
"""
#BasicBlock and BottleNeck block
#have different output size
#we use class attribute expansion
#to distinct
expansion = 1
def __init__(self, in_channels, out_channels, stride=1):
super(BasicBlock, self).__init__()
# residual function
self.residual_function = nn.Sequential(
nn.BatchNorm2d(in_channels), nn.ReLU(inplace=True),
nn.Conv2d(in_channels, out_channels, kernel_size=(3, 3), stride=(stride, stride), padding=(1, 1), bias=False),
nn.BatchNorm2d(out_channels), nn.ReLU(inplace=True),
nn.Conv2d(out_channels, out_channels * BasicBlock.expansion, kernel_size=(3, 3), padding=(1, 1), bias=False),
)
# shortcut
self.shortcut = nn.Sequential()
#the shortcut output dimension is not the same with residual function
#use 1*1 convolution to match the dimension
if stride != 1 or in_channels != BasicBlock.expansion * out_channels :
self.shortcut = nn.Sequential(
nn.Conv2d(in_channels, out_channels * BasicBlock.expansion, kernel_size=(1, 1), stride=(stride, stride), bias=False),
nn.BatchNorm2d(out_channels * BasicBlock.expansion)
)
def forward(self, x):
return self.residual_function(x) + self.shortcut(x)
코드 역시 실질적으로 달라지는 부분은 Residual Function에서 배치 정규화와 ReLU를 앞으로 옮겨준것이 전부이기 때문에 쉽게 이해할 수 있습니다.
