지난 포스팅에서 베이지안 통계에 대한 기본적인 개념에 대해서 알아보았습니다. 핵심은 사전 확률분포와 우도를 활용한 사후 확률분포의 추정을 수행하고 이를 기반으로 새로운 데이터에 대한 예측 분포를 구성하는 것 입니다. 이 과정애서 계산상의 편리를 위해 공액 사전 확률분포를 사용할 수 있음을 설명하였습니다.
오늘은 이를 더 자세하게 알아보기 위해 간단한 예제를 들고 와보았습니다. 베타-베르누이 모델(베타-이항분포 모델)을 기반으로 시작해보죠. 여기서 모형 이름은 베타-이항분포이지만 $\theta$ 자체는 베르누이 분포의 성공 확률로 정의되며 주변 확률분포가 베타-이항분포가 됩니다. 문제는 $N$번 문제를 던져서 앞면이 나오는 확률 $\theta \in [0, 1]$을 추정하고자 합니다. 여기서, $y_{n} = 1$이라면 $n$번째 시도에서 앞면, $y_{n} = 0$이라면 뒷면입니다. 그리고 $\mathcal{D} = \{ y_{1}, \dots, y_{N} \}$을 전체 데이터셋이라고 가정하겠습니다. 그리고 각 시도는 I.I.D 가정을 따르며 $y_{n} \sim \text{Ber}(\theta)$라고 가정하겠습니다. 즉, 목표는 어떻게 $p(\theta \mid \mathcal{D})$를 계산하느냐로 귀결됩니다.
1. 베르누이 우도(Bernoulli Likelihood)
각 시도가 I.I.D 가정을 따른다고 가정했기 때문에 전체 데이터셋 $\mathcal{D} = \{ y_{n} \}_{n = 1}^{N}$에 대한 우도는 다음과 같이 계산할 수 있습니다.
$$p(\mathcal{D} \mid \theta) = \prod_{n = 1}^{N} \theta^{y_{n}}(1 - \theta)^{1 - y_{n}} = \theta^{N_{1}}(1 - \theta)^{N_{0}}$$
여기서 $N_{1} = \sum_{n = 1}^{N} \mathbb{I}(y_{n} = 1)$이고 $N_{0} = \sum_{n = 1}^{N} \mathbb{I}(y_{n} = 0)$로 각각 앞면과 뒷면이 나온 횟수를 의미합니다. 베르누이 분포에서는 $(N_{1}, N_{0})$를 각각 충분통계량이라고 표현하고 데이터를 이 두 값으로 요약하면 $\theta$ 추론에 충분합니다. 그리고 $N = N_{1} + N_{2}$는 전체 표본의 크기가 됩니다.
2. 이항분포 우도(Binomial Likelihood)
동일한 문제를 $N$번 던져서 앞면이 $y$번 나왔다 라는 집계 데이터만으로도 충분히 표현할 수 있습니다.
$$p(\mathcal{D} \mid \theta) = \text{Bin}(y \mid N, \theta) = \begin{pmatrix} N \\ y \end{pmatrix} \theta^{y}(1 - \theta)^{N - y}$$
여기서 $\begin{pmatrix} N \\ y \end{pmatrix}$는 $\theta$와 무관한 스케일 상수로 베르누이 우도와 $\theta$에 대해 비례하므로 베르누이 우도 그리고 이항분포 우도는 $\theta$ 추론에서 동일합니다.
3. 사전분포(Prior)
베르누이 우도와 이항분포 우도에 대한 공액 사전확률분포는 베타 분포로 알려져 있습니다. 즉, $p(\theta) \propto \theta^{\tilde{\alpha} - 1}(1 - \theta)^{\tilde{\beta} - 1} \propto \text{Beta} (\theta \mid \tilde{\alpha}, \tilde{\beta})$입니다. 여기서 $\tilde{\alpha} > 0$와 $\tilde{\beta} > 0$은 모두 하아퍼파라미터로 “가상의 성공·실패 횟수”처럼 해석되어 가짜(pseudo) count 라고도 부릅니다.
4. 사후분포(Posterior)
이제 준비는 끝났습니다. 사전분포와 베르누이 우도를 곱하면 다음과 같습니다.
$$\begin{align} p(\theta\mid D) &\propto \theta^{N_1}(1-\theta)^{N_0}\; \theta^{\tilde\alpha-1}(1-\theta)^{\tilde\beta-1}\\ &\propto \operatorname{Beta}\bigl(\theta\mid\tilde\alpha+N_1,\;\tilde\beta+N_0\bigr)\\ &=\operatorname{Beta}(\theta\mid\hat\alpha,\hat\beta) \end{align}$$
즉, $\hat{\alpha} = \tilde{\alpha} + N_{1}$이고 $\hat{\beta} = \tilde{\beta} + N_{0}$로 업데이트 규칙이 결정됩니다. 여기서, 사후분포도 베타 분포이므로 “베타는 베르누이(바이노미얼)의 공액 사전”이라 말합니다. 그리고 $\tilde{N} = \tilde{\alpha} + \tilde{\beta}$은 등가 표본 크기(equivalent sample size)로 실제 표본 크기 $N$과 동일한 역할을 하며 사전의 영향력을 강화합니다.
결국, “가상(사전) 성공·실패 + 실제 성공·실패 = 사후 성공·실패”로 수행됩니다. 이는 베이지안 업데이트가 단순 덧셈으로 끝나므로, 계산과 해석이 모두 매우 직관적입니다.
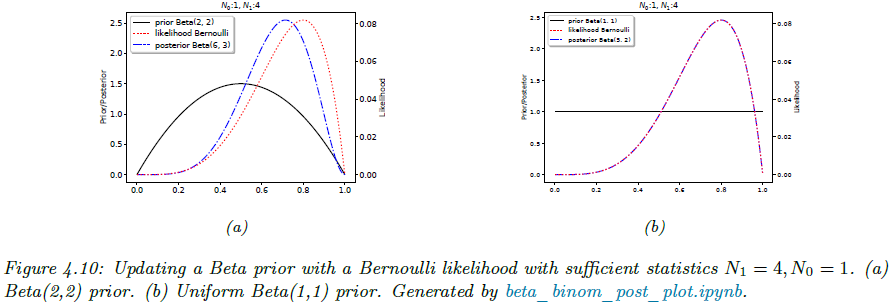
실제로 간단한 예시를 들어보겠습니다. 그림 4.10 (a)와 같이 사전확률을 $\text{Beta}(2, 2)$, 즉 $ \tilde{\alpha} = \tilde{\beta} = 2 $라고 설정했다고 가정하겠습니다. 이 뜻은 “이미 앞면을 2번, 뒷면을 2번 본 것 같다”는 약한 신념을 의미합니다. 즉, $\theta \approx 0.5$일거라고는 기대는 하고 있지만 강한 믿음은 가지지 않습니다. 위 그림에서 빨간선이 사전확률분포 $p(\theta)$, 검은선이 우도함수 $p(\mathcal{D} \mid \theta)$, 그리고 파란선이 사후확률분포 $p(\theta \mid \mathcal{D})$를 의미합니다. 결국 파란선인 사후확률분포는 파란선은 빨간·검은 선 사이에서 타협(compromise) 한 형태가 됩니다. 이때, 데이터가 충분히 많아지면 검은선 쪽(우도)으로 더 기울고, 데이터가 적으면 빨간선(사전) 영향이 더 커지게 되죠.
이번에는 그림 4.10 (b)와 같이 사전확률을 $\text{Beta}(1, 1) = \text{Unif}(0, 1)$, 즉 $ \tilde{\alpha} = \tilde{\beta} = 1$라고 설정했다고 가정하겠습니다. 이는 이전 예시와는 다르게 $\theta$에 대해 어떠한 가정도 하지 않는 균등분포로 사전확률분포의 등가 표본크기 $\tilde{N} = \tilde{\alpha} + \tilde{\beta} = 2$에서도 볼 수 있다싶이 영향력이 아주 작습니다. 결과적으로 사후확률분포를 추정할 때 사전 정보가 사실상 “손 떼고 관망”하므로, 데이터만으로 추정이 진행됩니다.
5. 사후 최빈값(Posterior mode) - MAP 추정(MAP estimate)
베이즈 정리를 통해 저희는 데이터셋 $\mathcal{D}$가 주어졌을 때 모델의 파라미터 $\theta$의 사후 확률분포 $p(\theta \mid \mathcal{D})$를 계산할 수 있었습니다. 이제 이 사후 확률분포가 주어졌을 때 가장 나올법한 파라미터를 선택해야겠죠? 이 파라미터 값이 바로 사후 최빈값이라고 부르며 이 과정을 MAP 추정이라고 합니다.
$$\begin{align} \hat{\theta}_{\text{MAP}} &= \text{argmax}_{\theta} p(\theta \mid \mathcal{D}) \\ &= \text{argmax}_{\theta} \log p(\theta \mid \mathcal{D}) \\ &= \text{argmax}_{\theta} \left[ \log p(\theta) + \log p(\mathcal{D} \mid \theta) \right] \end{align}$$
즉, 사전 확률분포 $p(\theta)$와 우도함수 $p(\mathcal{D} \mid \theta)$의 로그를 더해 거장 큰 $\theta$를 선택하면 됩니다. 이전의 예시에서 보았던 베타‑베르누이 모델에서의 MAP를 예시로 들어보도록 하겠습니다. 사전 $\tilde{\alpha}$와 $\tilde{\beta}$ 그리고 실제 관측결과 $N_{1}$과 $N_{0}$를 결합하면 다음과 같이 얻을 수 있습니다. [Section 4.5 Regularization - 2]
$$\hat{\theta}_{\text{MAP}} = \frac{\tilde{\alpha} + N_{1} - 1}{(\tilde{\alpha} + N_{1} - 1) + (\tilde{\beta} + N_{0} - 1)}$$
그리고 일전에 보았던 특수한 예시 $\tilde{\alpha} = \tilde{\beta} = 2$를 대입하면 $\hat{\theta}_{\text{MAP}} = \frac{N_{1} + 1}{N + 2}$가 되죠. 이는 분모에 +1을 함으로써 약간의 스무딩 효과(add-one smoothing)를 주어 너무 과하게 관측결과에 의존하지 않도록 하는 역할을 합니다.
그리고 $\tilde{\alpha} = \tilde{\beta} = 1$을 대입한다면 $\hat{\theta}_{\text{MAP}} = \frac{N_{1}}{N}$가 되죠. 이 결과는 기본적으로 MLE와 동일합니다. 왜냐하면 $\tilde{\alpha} = \tilde{\beta} = 1$라면 베타분포는 균등분포와 동일해지므로 $p(\theta) \propto 1$이 됩니다. 따라서, $\log p(\theta) \propto 0$이 되어 사전 정보는 MAP 추정에 어떠한 영향도 주지 못하므로 이는 기존의 MLE와 동일해지는 것이죠. 이 경우 앞면이 한번도 안나오는 0-카운트 문제가 발생한다면 $\hat{\theta}_{\text{MAP}} = \frac{N_{1}}{N} = 0$이 되므로 과도한 확신이 생겨 이상한 결과가 나오게 됩니다.
6. 사후 평균과 사후 분산(Posterior mean and Posterior variance)
이전에 보았던 사후 모드는 사후 확률분포 $p(\theta \mid \mathcal{D})$에서 가장 가능성 높은 한 점 $\hat{\theta}_{\text{MAP}} = \text{argmax}_{\theta} p(\theta \mid \mathcal{D})$를 수행하는 점 추정 방식입니다. 그러나 분포가 비대칭적이거나 다봉(multi-modal) 분포일 때 점 하나로 전체 불확실성을 설명하기에는 힘듭니다. 이에 비해 사후 평균은 분포를 적분하여 계산하여 더 안정적이고 일관적인 추정을 수행할 수 있습니다.
만약, 사후 분포가 $p(\theta \mid \mathcal{D}) = \text{Beta} (\theta \mid \hat{\alpha}, \hat{\beta})$라면 사후 평균은 다음과 같이 계산됩니다.
$$\mathbb{E}[\theta \mid \mathcal{D}] = \frac{\hat{\alpha}}{\hat{\alpha} + \hat{\beta}} = \frac{\hat{\alpha}}{\hat{N}}$$
여기서, $\hat{N} = \hat{\alpha} + \hat{\beta}$는 사후 등가표본크기라고 부릅니다. 다음으로 사전 평균과 MLE의 볼록 결합을 보도록 하겠습니다. 먼저, 베타 분포의 사전 확률분포의 평균은 $m = \frac{\tilde{\alpha}}{\tilde{N}}$이고 $\tilde{N} = \tilde{\alpha} + \tilde{\beta}$이죠. 그리고 MLE는 $\hat{\theta}_{\text{MLE}} = \frac{N_{1}}{N}$이고 $N = N_{1} + N_{0}$입니다. 이제 사후 평균을 전개하면 다음과 같죠.
$$\begin{align} \mathbb{E}[\theta \mid \mathcal{D}] &= \frac{\tilde{\alpha} + N_{1}}{\tilde{\alpha} + N_{1} + \tilde{\beta} + N_{0}} \\ &= \frac{\tilde{N}}{N + \tilde{N}} m + \frac{N}{N + \tilde{N}}\hat{\theta}_{\text{MLE}} \\ &= \lambda m + (1 - \lambda) \hat{\theta}_{\text{MLE}} \end{align}$$
여기서 $\lambda = \frac{\tilde{N}}{N + \tilde{N}}$는 가중치로 사전 등가표본크기 $\tilde{N}$이 클수록 커지게 되겠죠. 즉, 사전 정보가 강할수록 사후 평균이 $m$쪽으로 더 강하게 끌려갑니다. 이제, 데이터가 더 많이지게 되면 $N$이 커지게 되어 $N > \tilde{N}$이 될 것입니다. 따라서, $\lambda \approx 0$이 되므로 사후 평균이 거의 MLE와 유사한 결과를 가지게 되고 이는 사전 영향이 희미하다는 것을 의미합니다.
사후 평균을 구했다면 사후 분산이라는 것도 구해볼 수 있지 않을까요? 이것이 바로 베이지안 통계의 핵심입니다. 현재 주어진 데이터셋 $\mathcal{D}$로 추정한 파라미터 $\theta$에 대한 불확실성이죠. 가장 간단하면서 널리 쓰이는 방법이 사후 표준편차(posterior standard deviation), 또는 표준오차(standard error) 를 구해 함께 제시하는 것입니다.
$$\text{se}(\theta) = \sqrt{\mathbb{V}[\theta \mid \mathcal{D}]}$$
즉, 사후 분산의 제곱근이 곧 추정치의 ‘±오차 폭’ 을 나타냅니다. 베타 사후 확률분포에서 분산 공식을 구해보도록 하죠. 베르누이 모델에서 $\hat{\alpha} = \tilde{\alpha} + N_{1}$ 그리고 $\hat{\beta} = \tilde{\beta} + N_{0}$라고 가정할 때 $p(\theta \mid \mathcal{D}) = \text{Beta} (\theta \mid \hat{\alpha}, \hat{\beta})$라고 쓸 수 있죠. 그러면 베타 분포의 분산은 닫힌 형태로 다음과 같이 쉽게 구할 수 있습니다.
$$\mathbb{V}[\theta \mid \mathcal{D}] = \frac{\hat{\alpha}\hat{\beta}}{(\hat{\alpha} + \hat{\beta})^{2}(\hat{\alpha} + \hat{\beta} + 1)}$$
이를 사후 평균 $\mathbb{E}[\theta \mid \mathcal{D}] = \frac{\hat{\alpha}}{\hat{\alpha} + \hat{\beta}}$로 작성해보면 다음과 같습니다.
$$\mathbb{V}[\theta \mid \mathcal{D}] = \mathbb{E}[\theta \mid \mathcal{D}]^{2} \frac{\hat{\beta}}{\hat{\alpha}} \frac{1}{1 + \hat{\alpha} + \hat{\beta}}$$
만약, 관측치가 사전보다 훨씬 많다면 $\hat{\alpha} \approx N_{1}$ 이고 $\hat{\beta} \approx N_{0}$ 이기 때문에 $\hat{\alpha} + \hat{\beta} \approx N$이 됩니다. 따라서, 다시 한번 다음과 같이 쓸 수 있죠.
$$\mathbb{V}[\theta \mid \mathcal{D}] \approx \frac{N_{1}N_{0}}{N^{3}} = \frac{\hat{\theta}_{\text{MLE}} (1 - \hat{\theta}_{\text{MLE}})}{N}$$
따라서 표준오차는 다음과 같습니다.
$$\sigma = \sqrt{\mathbb{V}[\theta \mid \mathcal{D}]} \approx \sqrt{\frac{N_{1}N_{0}}{N^{3}}} = \sqrt{\frac{\hat{\theta}_{\text{MLE}} (1 - \hat{\theta}_{\text{MLE}})}{N}}$$
위 사후 분산식을 해석해보도록 하겠습니다. 1) 표본 크기가 4배 늘면 표준오차가 절반으로 줄어들어 데이터가 많을수록 불확실성이 빠르게 줄어드는 것을 볼 수 있죠. 2) 앞면 확률이 50 %라고 추정될 때가 가장 “애매”하므로 불확실성(분산)이 최대가 됩니다. 3) 거의 항상 앞면(또는 뒷면)이 나올 때는 동전이 편향됐음을 쉽게 확신할 수 있으므로 분산이 작습니다. 4) $N$이 작을 때는 $\tilde{\alpha}$와 $\tilde{\beta}$ 도 함께 들어가므로 사전에 따라 불확실성 크기가 달라집니다.
7. 사후 예측분포(Posterior Predictive)
이제 파라미터 추정까지 수행하였으니 마지막 단계는 추정된 파라미터를 이용해서 새로운 데이터가 입력되었을 때 그에 맞는 예측을 수행해주어야합니다. 가장 대표적으로 쓰이는 방법이 플러그-인(Plug-in) 근사라고 불리는 방법으로 훈련 데이터셋 $\mathcal{D}$를 이용해 파라미터 $\hat{\theta}(\mathcal{D})$를 추정한 뒤 이를 모델에 그대로 대입하여 $p(y \mid \hat{\theta})$를 사용하는 것 입니다.
하지만, 이 플러그-인 방법은 과적합을 초래할 수도 있습니다. 예를 들어, 동전을 세 번 던져서 $N = 3$ 모두 앞면이 나왔다고 가정하겠습니다. 이때, MLE는 $\hat{\theta}_{\text{MLE}} = 1$이 되겠죠. 만약, 이 값을 그대로 모델에 대입하면 뒷면은 절대 나오지 않는 다고 예측하게 됩니다. 이는 너무 극단적인 결론이며 절대 이루어질 수 없죠. 이를 완화하려면 MAP 추정을 통해 대입하는 방법이 있습니다. 하지만 여기서는 완전 베이지안(fully Bayesian) 접근을 소개합니다. 즉, $\theta$를 한 점으로 고정하지 않고 적분(marginalization)하여 사후 확률분포 전체를 활용하는 것이죠.
다시 베르누이 모델로 돌아가서 생각해보도록 하겠습니다. 미래 관측치를 예측할 때 파라미터 $\theta$를 적분해서 얻는 사후 예측분포를 살펴보도록 하겠습니다.
$$\begin{align} p(y = 1 \mid \mathcal{D}) &= \int_{0}^{1} p(y = 1 \mid \theta) p(\theta \mid \mathcal{D}) \\ &= \int_{0}^{1} \theta \text{Beta}(\theta \mid \hat{\alpha}, \hat{\beta}) \\ &= \mathbb{E}[\theta \mid \mathcal{D}] \\ &= \frac{\hat{\alpha}}{\hat{\alpha} + \hat{\beta}} \end{align}$$
쉽게 보면 $p(y = 1 \mid \theta)$라는 거는 $\theta$ 자체가 앞면이 나올 확률을 의미하기 때문에 $p(y = 1 \mid \theta) = \theta$가 됩니다. 그리고 저희가 사후분포 $p(\theta \mid \mathcal{D}) = \text{Beta} (\theta \mid \hat{\alpha}, \hat{\beta})$로 구했기 때문에 위와 같이 쓸 수 있는 거죠. 그리고 적분구간은 저희가 $\theta \in [0, 1]$이라고 가정했기 때문에 저렇게 쓸 수 있습니다.
이전에 저희가 "+1 스무딩" 효과를 얻기 위해 베타 사전 $\text{Beta} (2, 2)$를 썻지만 완전 베이지안 방식에서는 균등 사전만으로도 동일한 효과를 얻을 수 있습니다. 사전 확률분포를 $p(\theta) = \text{Beta}(\theta \mid 1, 1)$이라고 가정하면 $p(y = 1 \mid \mathcal{D}) = \frac{N_{1} + 1}{N_{1} + N_{0} + 2}$가 됩니다. 이 식이 바로 라플라스의 계승 규칙으로, “아무것도 모르는 상태(균등 사전)”에서도 실제 관측 + 1 회를 더한 것과 같은 효과가 나타납니다.
앞서 베르누이 모델은 단 한번의 미래 던지기에 대한 예측이였다면 이번에는 $M > 1$, 즉 여러 번의 미래 동전 던지기에서 앞면이 몇 번 나올지를 예측해보도록 하겠습니다. 즉, 이항분포 모델을 사용할 것 입니다. 이항분포 모델을 기반으로 사후 예측분포 적분식을 계산하면 다음과 같습니다.
$$\begin{align} p(y \mid \mathcal{D}, M) &= \int_{0}^{1} \text{Bin}(y \mid M, \theta) \text{Beta}(\theta \mid \hat{\alpha}, \hat{\beta}) \; d\theta \\ &= \begin{pmatrix} M \\ y \end{pmatrix} \frac{1}{B(\hat{\alpha}, \hat{\beta})} \int_{0}^{1} \theta^{y} (1 - \theta)^{M - y} \theta^{\hat{\alpha} - 1}(1 - \theta)^{\hat{\beta} - 1} \; d\theta \\ &= \begin{pmatrix} M \\ y \end{pmatrix} \frac{1}{B(\hat{\alpha}, \hat{\beta})} B(y + \hat{\alpha}, M - y + \hat{\beta}) = Bb(y \mid M, \hat{\alpha}, \hat{\beta}) \end{align}$$
이 분포를 복합 베타-이항분포라고 부르며 이항분포의 파라미터 $\theta$를 사후 베타분포로 적분한 결과입니다.
8. 주변우도(Marginal likelihood)
모델 $\mathcal{M}$의 주변우도는 다음과 같이 정의됩니다.
$$p(\mathcal{D} \mid \mathcal{M}) = \int p(\theta \mid \mathcal{M}) p(\mathcal{D} \mid \theta, \mathcal{M}) \; d\theta$$
특정 모델의 파라미터를 추론할 때는 이 항이 $\theta$에 대해서 상수이기 때문에 무시해도 됩니다. 하지만, 서로 다른 두 모델을 비교하거나 하이퍼파라미터를 데이터로부터 추정할 때는 매우 중요한 역할을 수행합니다.
다시 이전 예시로 돌아가서 베타-베르누이 모델에서의 주변우도를 확인해보도록 하겠습니다. 일반적으로는 $p(\mathcal{D} \mid \mathcal{M})$을 구하는 것은 아주 어렵습니다. 하지만, 베타-베르누이 모델에서는 사후 확률분포의 정규화 상수와 사전 확률분포의 정규화 상수의 비율로 닫힌 형태로 표현되죠.
일단 사후 확률분포는 $a^{'} = a + N_{1}$ 그리고 $b^{'} = b + N_{0}$라고 했을 때 $p(\theta \mid \mathcal{D}) = \text{Beta} (\theta \mid a^{'}, b^{'})$입니다. 여기서 사후 확률분포의 정규화 상수는 $B(a^{'}, b^{'})$입니다. 이제 베이즈 정리를 통해 이 식을 전개해보겠습니다.
$$\begin{align} p(\theta \mid \mathcal{D}) &= \frac{p(\mathcal{D} \mid \theta) p(\theta)}{p(\mathcal{D})} \\ &= \frac{1}{p(\mathcal{D})} \left[ \frac{1}{B(a, b)} \theta^{a - 1} (1 - \theta)^{b - 1} \right] \left[ \begin{pmatrix} N \\ N_{1} \end{pmatrix} \theta^{N_{1}} (1 - \theta)^{N_{0}} \right] \\ &= \begin{pmatrix} N \\ N_{1} \end{pmatrix} \frac{1}{p(\mathcal{D})} \frac{1}{B(a, b)} \theta^{a + N_{1} - 1} (1 - \theta)^{b + N_{0} - 1} \end{align}$$
여기서 공액 사전확률에 의해 $p(\theta \mid \mathcal{D})$ 역시 베타 분포가 되므로 다음과 같이 쉽게 $p(\mathcal{D})$를 구할 수 있습니다.
$$\begin{align} &B(a + N_{1}, b + N_{0}) = \begin{pmatrix} N \\ N_{1} \end{pmatrix} \frac{1}{p(\mathcal{D})} \frac{1}{B(a, b)} \\ \Rightarrow& p(\mathcal{D}) = \begin{pmatrix} N \\ N_{1} \end{pmatrix} \frac{B(a + N_{1}, b + N_{0})}{B(a, b)} \end{align}$$
주변우도는 모델 선택에 있어 매우 중요한 역할을 합니다. 서로 다른 사전 정보가 주어졌때 $p(\mathcal{D} \mid \mathcal{M})$이 크다는 것은 데이터가 그만큼 모델을 잘 설명한다는 의미이기 때문이죠. 또한, 향후에 더 자세하게 알아볼 하이퍼파라미터 추정 과정에서 중요합니다. 사전 정보 $(a, b)$를 데이터에 맞추어 자동으로 조정하는 경험적 베이즈 추정 과정에서는 주변 우도를 최대화 하여 구합니다. 이와 같이 베타–베르누이처럼 해석적(analytical) 계산이 가능한 경우, 데이터가 들어오면 사전–사후 정규화 상수의 변동만으로 모델 증거를 곧바로 얻을 수 있다는 장점이 있습니다.
9. 공액 사전의 혼합 (Mixtures of Conjugate Priors)
베타 부포는 이항 우도의 공액 사전 확률분포이기 때문에 사후 확률분포를 손쉽게 닫힌 형태로 표현할 수 있습니다. 하지만, 단일 베타 분포는 표현력이 제한적이죠. 예를 들어, 카지노의 동전이 공정할 수도 있겠지만, 앞면 쪽으로 치우쳐져 있을 수도 있다고 믿는 다면, 이런 “두 가지 가능성이 동등하게 존재”한다는 사전 신념은 하나의 베타 분포로는 표현할 수 없습니다. 간단한 예시와 함께 확인해보겠습니다.
$$p(\theta) = 0.5 \text{Beta} (\theta \mid 20, 30) + 0.5 \text{Beta} (\theta \mid 30, 10)$$
첫번째 베타 분포 $\text{Beta} (20, 20)$은 동전이 공정하다는 사전정보, 그리고 두번째 베타 분포 $\text{Beta} (30, 10)$은 동전이 앞면쪽으로 편향되어있다는 사전정보입니다. 이를 혼합 가중치 $p(h = k)$와 잠재 지시 변수 $h$를 도입하여 표현할 수 있습니다.
$$p(\theta) = \sum_{k} p(h = k)p(\theta \mid h = k)$$
여기서 $p(\theta \mid h = k)$는 베타 분포이고 $p(h = k)$가 혼합 가중치입니다. 이제 사후 확률분포의 형태를 구해보겠습니다.
$$\begin{cases} p(\theta \mid \mathcal{D}) &= \sum_{k} p(h = k \mid \mathcal{D})p(\theta \mid \mathcal{D}, h = k) \\ p(h = k \mid \mathcal{D}) &= \frac{p(h = k) p(\mathcal{D} \mid h = k)}{\sum_{k^{'}} p(h = k^{'}) p(\mathcal{D} \mid h = k^{'})} \end{cases}$$
여기서 $p(\mathcal{D} \mid h = k)$는 혼합 성분 $k$에 대한 주변 우도입니다.
'인공지능 > Probabilistic Machine Learning (intro)' 카테고리의 다른 글
| [PML intro] Ch4 Statistics (Sec4.6 Bayesian Statistics - 4) (0) | 2025.07.19 |
|---|---|
| [PML intro] Ch4 Statistics (Sec4.6 Bayesian Statistics - 3) (2) | 2025.07.18 |
| [PML intro] Ch4 Statistics (Sec4.6 Bayesian Statistics - 1) (3) | 2025.07.16 |
| [PML intro] Ch4 Statistics (Sec4.5 Regularization - 4) (0) | 2025.07.15 |
| [PML intro] Ch4 Statistics (Sec4.5 Regularization - 3) (2) | 2025.07.14 |
