지난 포스팅에서는 딥 러닝에서도 거의 필수적으로 활용되는 가중치 감쇠 중 하나인 $l_{2}$ 정규화에 대해서 알아보았습니다. 핵심은 가중치들의 값이 너무 큰 값으로 학습되지 않고 골고루 학습될 수 있게 손실함수에 $C(w) = ||w||_{2}^{2}$을 더해주는 것입니다. 오늘은 정규화와 관련된 다양한 기법에 대해서 알아보도록 하겠습니다.
1. 검증 데이터셋을 이용한 정규화 기법 선택(Picking the Regularizer using a Validation Set)
기본적으로 정규화의 세기를 조정하는 $\lambda$는 하이퍼파라미터로 데이터셋에 따라 적절하게 선택해주어야합니다. 만약, $\lambda$가 너무 작으면 혼련 손실을 더 중시하게 되어 과적합의 위험이 커지고 반대로 $\lambda$가 너무 크면 패널티를 더 중시하여 과소적합의 위험이 있습니다.
이를 위해 가장 널리 쓰이는 해결책은 훈련 데이터를 훈련 데이터셋 $\mathcal{D}_{\text{train}}$과 검증 데이터셋 $\mathcal{D}_{\text{valid}}$로 분할한 뒤 검증 성능이 가장 좋은 $\lambda$를 선택하는 방법입니다. 일반적으로는 8:2 정도로 나누는 편이지만 상황에 따라서 달라질 수 있습니다. 일단, 정규화항이 포함된 경험 위험은 다음과 같이 정의할 수 있습니다.
$$R_{\lambda}(\theta, \mathcal{D}) = \frac{1}{|\mathcal{D}|} \sum_{(x, y) \in \mathcal{D}} l(y, f(x; \theta)) + \lambda C(\theta)$$
그리고 각 후보 정규화 세기값 $\lambda$에 따라서 훈련 데이터셋 $\mathcal{D}_{\text{train}}$에서 학습을 진행하고 파라미터 $\theta$를 추정합니다.
$$\hat{\theta}_{\lambda} (\mathcal{D}_{\text{train}}) = \text{argmin}_{\theta} R_{\lambda} (\theta, \mathcal{D}_{\text{train}})$$
이때, 어떤 식으로 $\lambda$ 후보군을 설정하는 지는 향후에 더 자세히 알아보도록 하겠습니다. 다음 단계는 특정값 $\lambda$ 을 기반으로 훈련된 파라미터 $\hat{\theta}_{\lambda}$을 검증 데이터셋 $\mathcal{D}_{\text{valid}}$에서 평가를 진행하여 검증 위험을 계산합니다.
$$R_{\lambda}^{\text{valid}} = R_{0} (\hat{\theta}_{\lambda}(\mathcal{D}_{\text{train}}), \mathcal{D}_{\text{valid}})$$
여기서 $R_{\lambda}^{\text{valid}}$는 실제 데이터셋 분포 $p^{*}(x, y)$ 아래에서 기대 손실(모집단 위험 손실)을 추정하는 값입니다. 마지막으로 $\lambda$의 후보군 집합에 대해서 모두 위 과정을 거치고 가장 작은 기대 손실을 가지게 되는 $\lambda$를 선택하여 사용하면 됩니다.
$$\lambda^{*} = \text{argmin}_{\lambda \in \mathcal{S}} R^{\text{val}}_{\lambda}$$
최종 $\lambda^{*}$를 얻었다면 이를 이용하여 기존의 훈련 데이터셋 $\mathcal{D}_{\text{train}}$과 검증 데이터셋 $\mathcal{D}_{\text{valid}}$를 하나로 합쳐서 재학습을 진행하여 파라미터를 다시 추정합니다.
$$\hat{\theta}^{*} = \text{argmin}_{\theta} R_{\lambda^{*}} (\theta, \mathcal{D}_{\text{train}} \cup \mathcal{D}_{\text{valid}})$$
2. 교차검증(Cross‑validation)
바로 직전에 보았던 훈련-검증 데이터셋의 8:2 분할 방식은 직관적이고 쉽지만 전체 데이터의 규모가 너무 작으면 신뢰도가 떨어질수도 있습니다. 이를 해결하기 위한 가장 직관적인 아이디어가 바로 교차검증입니다.

그림 4.6만 봐도 교차검증의 기본적인 개념을 아주 쉽게 이해할 수 있습니다. 전체 데이터셋이 있다면 이를 $K$겹으로 분할합니다. 예를 들어 20개의 데이터로 구성된 데이터셋이 있고 이를 5겹으로 나눈다고 가정하면 각 겹에 포함된 데이터의 개수는 4개씩 포함됩니다. 물론 항상 정확하게 떨어지지는 않겠지만 최대한 비슷한다고 나눈다고 하겠습니다. 그러면 총 $K$개의 폴드 $\mathcal{D}_{1}, \dots, \mathcal{D}_{K}$를 얻게 됩니다.
다음 단계는 라운드-로빈 학습/평가 방식을 진행합니다. 즉, 각 $k \in \{1, \dots, K\}$에 대해서 $k$번째 폴드 $\mathcal{D}_{k}$는 평가 데이터셋으로 사용하고 나머지 폴드들 $\mathcal{D}_{-k}$ 은 학습 데이터셋로 삼는 것입니다. 그리고 이를 $k$번 반복하고 평균 위험을 얻어서 교차검증 위험을 얻게 됩니다.
$$R^{\text{cv}}_{\lambda} = \frac{1}{K} \sum_{k = 1}^{K} R_{0} (\hat{\theta}_{\lambda}(\mathcal{D}_{-k}), \mathcal{D}_{k})$$
여기서 $K = N$, 즉 데이터셋의 개수와 폴드의 개수를 동일하게 두면 매번 1개의 샘플을 평가에 사용하고 나머지 $N - 1$개의 데이터셋들을 학습에 사용하게 됩니다. 이를 Leave-one-out(LOO) CV라고 부릅니다. 이 방식은 데이터가 매우 적을 때 일반화 추정 편향이 가장 낮지만 모델 학습을 $N$번 반복해야하므로 계산량이 매우 큽니다.
위 단계를 거쳐서 저희가 최적화하고 싶어하는 하이퍼파라미터를 선택하고 다시 사용 가능한 모든 데이터셋을 취합하여 파라미터를 재추정하게 됩니다.
$$\begin{cases} \hat{\lambda} &= \text{argmin}_{\lambda \in \mathcal{S}} R_{\lambda}^{\text{cv}} \\ \hat{\theta} &= \text{argmin}_{\theta} R_{\hat{\lambda}} (\theta, \mathcal{D}) \end{cases}$$
향후에 CV 기법에 대한 더 자세한 이론적 배경을 다루도록 하겠습니다. 하지만, 교차검증은 모델별 추정 위험 $\hat{R}_{\lambda}$를 점 추정치로만 제공하고 추정 결과에 대한 신뢰구간과 같은 불확실성을 함께 제공하지 못하기 때문에 아주 작은 차이를 과신할 가능성이 높습니다. 이러한 문제를 해겨라기 위해 교차검증 시 학습 루프에서 각 샘플 $n$이 속하지 않은 폴드로 학습한 파라미터 $\hat{\theta}_{-n}$을 이용해서 손실을 측정하면 다음을 얻을 수 있습니다.
$$\mathcal{L}_{n} = l(y_{n}, f(x_{n}; \hat{\theta}_{\lambda}(\mathcal{D}_{-n})))$$
여기서 $\mathcal{L}_{n}$은 $\lambda$에 의존하지만 편의상 기호 $\lambda$는 생략하도록 하겠습니다. 그리고 교차검증 위험위 표본평균 $\hat{\mu} = \frac{1}{N} \sum_{n = 1}^{N} \mathcal{L}_{n}$과 표본분산 $\hat{\sigma}^{2} = \frac{1}{N} \sum_{n = 1}^{N} (\mathcal{L}_{n} - \hat{\mu})^{2}$을 계산할 수 있습니다. 여기서, $\hat{\mu}$는 교차검증 위험의 표본평균이고 $\hat{\sigma}^{2}$은 내재 변동성으로 샘플 간의 손실 분산을 의미합니다.
표본 평균의 불확실성은 $\text{se}(\hat{\mu}) = \frac{\hat{\sigma}}{\sqrt{N}}$으로 근사하게 됩니다. 여기서, $\hat{\mu}$가 크면 데이터마다 손실 변동이 크다는 것을 의미하고 $\text{se}(\mu)$가 크면 $\hat{\mu}$ 자체가 불안정하다는 것을 의미합니다. 따라서, 교차검증으로 여러 $\lambda$ 후보값들에 대해 평가를 수행한 뒤 가장 낮은 $\hat{\mu}$을 갖는 모델을 찾은 뒤 그 모델의 위험 + 1SE 이하에 해당하는 모델 중 가장 단순한 (파라미터 개수가 작거나 또는 $\lambda$가 큰) 모델을 선택합니다. 이러한 과정을 표준 오차 규칙이라고 부르며 직관적으로는 교차검증 손실 값이 약간 커도 오차 막대(SE) 안이면 “통계적으로 동일”하니,
복잡도를 줄여 과적합 리스크를 완화하자는 휴리스틱입니다.
3. 조기종료(Early Stopping)
대부분의 학습 알고리즘은 반복적(Iterative) 으로 파라미터를 갱신합니다. 학습 초반에는 모델이 일반적인 패턴을 익히지만, 반복이 계속되면 훈련 데이터의 노이즈 (= “잡음”)까지 외워 과적합이 발생합니다. 조기종료는 검증 성능이 악화되기 시작하는 시점에서 학습을 멈춰 과적합을 방지하는 매우 실용적인 정규화 방법입니다.
동작원리도 매우 간단합니다. 훈련 루프 내에서 매 에폭 또는 일정 스텝마다 훈련 손실과 검증 손실을 기록해놓습니다. 검증 손실이 더 이상 감소하지 않으면 또는 지정한 횟수만큼 연속으로 악화된다면 현재 파라미터를 최종 모델로 채택하고 학습을 종료합니다. TensorFlow나 PyTorch와 같은 딥 러닝 학습 프레임워크에서는 보통 “patience” 라는 하이퍼파라미터를 둬서 검증 손실이 $p$번 연속으로 나빠질 때까지 기다린 뒤 중지합니다.
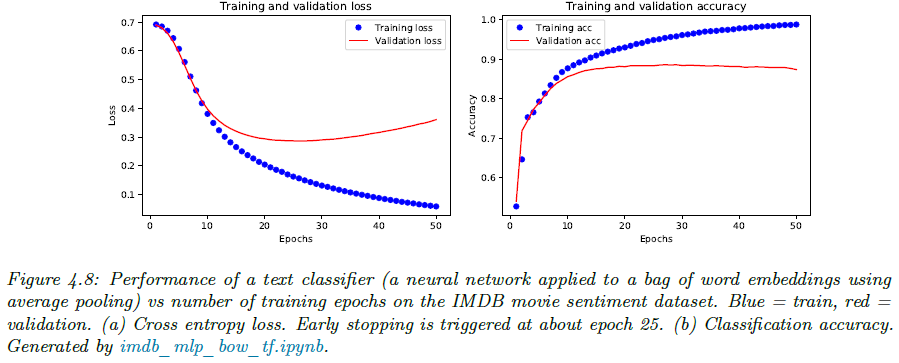
조기종료는 사실 아주 단순하지만 강력한 정규화 기법입니다. 그림 4.8에서 보이는 것과 같이 모델은 학습 초기에 주요 구조(패턴)만 학습하여 일반화 성능을 향상시키게 됩니다. 하지만, 학습 후기에 모델의 용량이 커지면서 훈련 데이터의 세세한 특성까지 적합하려고 하여 검증 성능을 약화하게 됩니다. 따라서, 조기종료로 학습 후기에 진입하기 전에 학습을 중단하게 되면 가중치가 아직 적당하게 작은 상태로 남아있게 되고 이는 가우시안 사전을 두는 $l_{2}$ 정규화 효과와 유사한 정규화 효과를 가지게 됩니다.
4. 추가 데이터 사용(Using More Data)
정규화를 가장 쉽게 해결하는 좋은 방법은 추가적인 데이터를 사용하는 것 입니다. 모델 복잡도를 그대로 두고 훈련 샘플 수 $N$를 늘리면 과적합 가능성이 점차 낮아집니다. 단, 정보가 풍부하고 중복이 적은 데이터라는 전제하에 그렇습니다.

그림 4.9는 다항식 차수(모델 복잡도)가 1, 2, 3, 10 인 네 가지 모델에 대해 훈련 데이터셋·평가 데이터셋 평균제곱오차(MSE)를 훈련 샘플 수 $N$의 함수로 그린 그래프입니다. 이런 그래프를 학습 그래프라고 부릅니다. 여기서, 수평 검은 선 : 베이즈 오차(Bayes error)로 진짜 모델(최적 예측기)가 갖는 불가피한 오차를 의미합니다. 이 예에서는 차수 2 다항식이 정답 모델이고 잡음 분산이 $\sigma^{2} = 4$를 노이즈 플로어라고 부릅니다.
위 그래프에서 차수 1인 모델은 $N$이 아무리 커져도 모델이 단순해서 평가 손실이 높습니다. 하지만, 차수 10인 복잡한 모델의 경우 훈련 오차와 평가 오차 사이의 간극이 크지만 $N$이 증가할 수록 서서히 좁혀집니다. 차수 2 그리고 차수 3인 모델은 베이즈 오차까지 비교적 빠르게 수렴합니다. 이는 추정할 파라미터가 적어 학습이 빠르기 때문입니다.
유연한 모델(차수 3·10)에서 초기 구간에 훈련 오차(파란 선)가 오히려 증가합니다. 이는 데이터가 늘수록 새로운 입력‑출력 조합이 생겨, 맞추기 어려운 패턴이 추가되기 때문입니다. 하지만, $N$이 충분히 크면 훈련 데이터셋과 평 데이터셋 분포가 비슷해지고,
두 오차가 수렴하며 모델의 최적 성능을 반영합니다. 결국, 데이터를 많이 확보하면, 복잡한 모델도 훈련·평 오차 차이가 줄어들어 과적합이 완화되고, (모델이 너무 단순하지 않은 한) 베이즈 오차—즉 노이즈 플로어—에 근접할 수 있습니다.
'인공지능 > Probabilistic Machine Learning (intro)' 카테고리의 다른 글
| [PML intro] Ch4 Statistics (Sec4.6 Bayesian Statistics - 2) (1) | 2025.07.17 |
|---|---|
| [PML intro] Ch4 Statistics (Sec4.6 Bayesian Statistics - 1) (3) | 2025.07.16 |
| [PML intro] Ch4 Statistics (Sec4.5 Regularization - 3) (2) | 2025.07.14 |
| [PML intro] Ch4 Statistics (Sec4.5 Regularization - 2) (1) | 2025.07.11 |
| [PML intro] Ch4 Statistics (Sec4.5 Regularization - 1) (1) | 2025.07.10 |
