정규화의 핵심은 정규화 항 $C(\theta)$를 어떻게 정의하느냐에 따라서 달라집니다. 지난 포스팅에서 보았던 MAP는 $C(\theta)$를 추정하고자 하는 파라미터에 대한 사전 정보 $p(\theta)$로 정의하는 방식이였죠. 물론 다른 방식으로 정의할 수도 있겠죠? 오늘은 정규화의 대표적인 방식 중 하나인 가중치 감쇠(Weight Decay)에 대해서 알아보도록 하겠습니다.
기본적으로 MLE 또는 ERM만으로 모델을 학습하게 되면 고차 다항식처럼 파라미터가 많은 모델이 쉽게 과적합됩니다. 가중치 감쇠 또는 $l_{2}$ 정규화는 파라미터의 크기 자체에 패널티를 걸어 모델이 지나치게 요동치는 것을 방지하는 방식입니다. 간단한 문제를 정의해보도록 하겠습니다. $N$개의 데이터 쌍으로 구성된 훈련 데이터셋 $\mathcal{D} = \{ (x_{n}, y_{n}) \}_{n = 1}^{N}$ 입력 데이터 $x_{n} \in \mathbb{R}^{D}$와 타겟 데이터 $y_{n} \in \mathbb{R}$이 주어졌다고 가정하겠습니다. 그리고 모델을 $f(x; w) = \sum_{d = 0}^{D} w_{d}x_{d} = w^{T}\phi(x)$라고 하겠습니다. 여기서, $\phi(x) = [1, x, x^{2}, \dots, x^{D}]^{T}$는 다항식의 기저벡터로 정의되고 $w = [w_{0}, w_{1}. w_{2}, \dots, w_{D}]^{T}$는 학습하고자 하는 가중치 벡터입니다. 마지막으로 오차가 I.I.D 가정과 가우시안 분포를 따른다고 가정하면 다음과 같이 우도를 계산할 수 있습니다.
$$p(y \mid X, w, \sigma^{2}) = \prod_{n = 1}^{N} \mathcal{N}(y_{n} \mid w^{T}\phi(x_{n}), \sigma^{2})$$
여기서, $w^{T}\phi(x_{n})$은 가우시안 분포의 평균의 역할을 수행하고 $\sigma^{2}$은 가우시안 분포의 분산을 의미합니다. 이때, 분산은 데이터에 따라 모두 동일하게 고정된 값이라고 가정하겠습니다.
기본적으로 MLE는 고차 다항식의 차원 $D$이 커지고 데이터의 개수 $N$가 작아질수록 $w$를 최대한 키워서 훈련 데이터를 거의 통과점으로 맞출 수 있습니다. 그러면 예측 곡선이 과도하게 구불구불(wiggly)해지고 이로 인해 과적합이 발생하죠. 가장 대표적으로 라플라스 보간법을 생각해보시면 됩니다.
이를 해결하기 위한 방법으로 가우시안 사전 확률분포에 MAP 추정을 결합하는 방식을 생각해볼 수 있습니다. 평균이 0인 가우시안 사전 확률분포는 다음과 같습니다.
$$p(w) = \mathcal{N}(w \mid 0, \tau^{2}I) \Rightarrow -\log p(w) = \frac{1}{2\tau^{2}} ||w||_{2}^{2} + \text{const}$$
여기서 직관적으로 생각해보면 파라미터 $w$에 대한 가우시안 사전 확률분포의 분산 $\tau^{2}$이 작아질수록 $w$가 0 근처에 있어야한다는 압박을 부여합니다. 다음으로 로그 사후를 계산해보면 다음과 같습니다.
$$\begin{align} \mathcal{L}(\theta) &= -\log p(y \mid X, w) - \log p(w) + \text{const} \\ &= \frac{1}{2\sigma^{2}} ||y_Xw||_{2}^{2} + \frac{1}{2\tau^{2}} ||w||_{2}^{2} + \text{const} \end{align}$$
여기서 $X \in \mathbb{R}^{N \times (D + 1)}$은 모든 훈련벡터들을 행으로 쌓은 디자인 행렬입니다. 이제 위 식에서 상수항을 제거하고 $\lambda = \frac{\sigma^{2}}{\tau^{2}}$이라고 정의하면 다음의 최적화 문제를 풀어서 $w$를 구할 수 있습니다.
$$w_{\text{map}} = \text{argmin}_{w} \left[ \underbrace{||y - Xw||_{2}^{2}}_{\text{데이터 적합도}} + \lambda \underbrace{||w||_{2}^{2}}_{\text{가중치 패널티}}\right]$$
위 결과를 가중치 감쇠 또는 $l_{2}$ 정규화라고 부릅니다. 여기서 $\lambda > 0$가 커질수록 파라미터 $w$에 대한 패널티가 강해져서 $w$가 0으로 더 강하게 가까워집니다. 그러면 상대적으로 모델이 덜 유연하게 되어 과적합을 방지할 수 있겠죠. 심지어 이 식은 볼록 이차함수이기 때문에 미분을 통해서도 쉽게 닫힌 형태의 해를 구할 수 있습니다.
$$\begin{align} &\frac{\partial }{\partial w} \left( ||y - Xw||_{2}^{2} + \lambda ||w||_{2}^{2} \right) = -2X^{T}(y - Xw) + 2\lambda w = 0 \\ \Rightarrow& (X^{T}X + \lambda I)w = X^{T}y \\ \Rightarrow& w_{\text{ridge}} = (X^{T}X + \lambda I)^{-1}X^{T}y \end{align}$$
이 결과를 보통 릿지 회귀(Ridge Regression)이라고 합니다. 여기서 $\lambda = 0$이라면 일반적인 MLE와 동일하겠죠? $\lambda > 0$은 $X^{T}X$의 대각성분에 $\lambda$를 더해줌으로써 수치적 안정성도 개선할 수 있습니다.
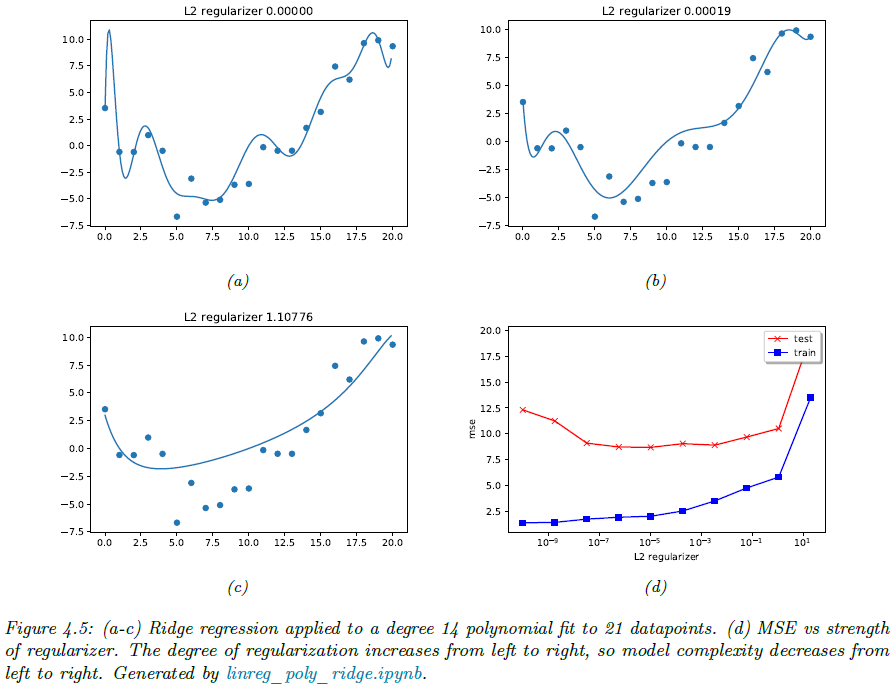
그림 4.5를 보도록 하겠습니다. 차원 $D = 14$ 그리고 데이터 개수 $N = 21$이라고 가정했을 때 $\lambda = 0$인 경우 (a)와 같이 크게 요동치지만 $l_{2}$ 정규화를 크게 적용할 수록 (b)와 (c)와 같이 그 구불구불함이 줄어들게 되죠. 하지만, 너무 큰 $\lambda$는 (d)와 같이 과소적합(underfitting)의 위험이 있기 때문에 추가적인 검증 데이터 또는 교차검증으로 사용하는 데이터에 따른 최적의 $\lambda$를 찾는 것이 중요합니다.
저희가 처음에 $p(w) = \mathcal{N}(w \mid 0, \tau^{2}I)$으로 가정하였기 때문에 $l_{2}$ 정규화의 형태로 나왔습니다. 하지만, 다른 분포로 가정하게 되면 $l_{1}$ 정규화인 라쏘 회귀(Lasso Regression) $||w||_{1}$으로 나오기도 하며 이는 특징 선별 효과도 부여합니다. 이 부분은 향후에 더 자세히 설명하도록 하겠습니다.
'인공지능 > Probabilistic Machine Learning (intro)' 카테고리의 다른 글
| [PML intro] Ch4 Statistics (Sec4.6 Bayesian Statistics - 1) (3) | 2025.07.16 |
|---|---|
| [PML intro] Ch4 Statistics (Sec4.5 Regularization - 4) (0) | 2025.07.15 |
| [PML intro] Ch4 Statistics (Sec4.5 Regularization - 2) (1) | 2025.07.11 |
| [PML intro] Ch4 Statistics (Sec4.5 Regularization - 1) (1) | 2025.07.10 |
| [PML intro] Ch4 Statistics (Sec4.4 Other Estimation Methods - 2) (3) | 2025.07.09 |
