안녕하세요. 지난 포스팅에서는 베르누이-베타 모델을 기반으로 베이지안 통계의 예시를 들어보았습니다. 오늘은 이를 조금 일반화시킨 디리클레-멀티모달 모델을 기반으로 베이지안 통계의 예시를 봐도록 하겠습니다. 기존에는 동전 던지기의 앞면이 나올 확률을 추정하는 거였다면 오늘은 주사위의 각 면이 나올 확률을 추정하는 것 입니다.
1. 우도(Likelihood)
먼저 범주형 분포에서 추출한 이산 랜덤 변수 $Y \sim \text{Cat}(\mathbf{\theta})$를 생각해보겠습니다. 여기서, $\mathbf{\theta} = ( \theta_{1}, \dots, \theta_{C} )$는 $C$개의 범주 각각이 나올 확률을 의미합니다.
$$\begin{align} p(\mathcal{D} \mid \mathbf{\theta}) &= \prod_{n = 1}^{N} \text{Cat}(y_{n} \mid \mathbf{\theta}) \\ &= \prod_{n = 1}^{N} \prod_{c = 1}^{C} \mathbf{\theta}_{c}^\mathbb{I}(y_{n} = c) \\ &= \prod_{c = 1}^{C} \mathbf{\theta}_{c}^{N_{c}} \end{align}$$
여기서 $N_{c} = \sum_{n = 1}^{N} \mathbb{I}(y_{n} = c)$는 범주 $c$가 등장한 횟수를 의미합니다. 즉, 범주별 등장 횟수 $N_{c}$만 주어진다면 데이터의 우도를 한 줄로 정리할 수 있습니다. 이는 다항 분포의 우도 표현과 동일한 구조로, 이후에 디리클레-다항 모델을 다룰 때 핵심이 됩니다.
2. 사전 분포(Prior)
범주형 분포의 공액 사전은 다변량 베타분포라고도 불리는 디리클레 분포입니다. 이 분포는 확률 심플렉스(Probabilisty Simplex)에 의해서 정의됩니다. 여기서 확률 심플렉스는 다음과 같습니다.
$$S_{K} = \{ \mathbf{\theta} \mid 0 \le \theta_{k} \le , \sum_{k = 1}^{K} \theta_{k} = 1 \}$$
즉, 확률 심플렉스라는 거는 기본적인 확률의 조건을 집합의 형태로 표현한 것이라고 보시면 됩니다. 다음으로 디리클레 분포의 PDF는 다음과 같습니다.
$$\text{Dir}(\mathbf{\theta} \mid \mathbf{\alpha}) = \frac{1}{B(\alpha)} \prod_{k = 1}^{K} \theta_{k}^{\alpha_{k} - 1} \mathbf{I}(\mathbf{\theta} \in S_{K})$$
여기서 $B(\alpha) = \frac{\prod_{k = 1}^{K} \Gamma(\alpha_{k})}{\Gamma \left( \sum_{k = 1}^{K} \alpha_{k} \right)}$로 정의되는 다변량 베타함수로 정의되는 정규화 상수입니다. 그리고 $\Gamma(\cdot)$는 감마함수이고 $\mathbf{\alpha} = (\alpha_{1}, \dots, \alpha_{K})$는 양수 하이퍼파라미터입니다. 벌써 수식이 많아서 어지러우신가요?... 아쉽지만 이제부터 시작입니다!!
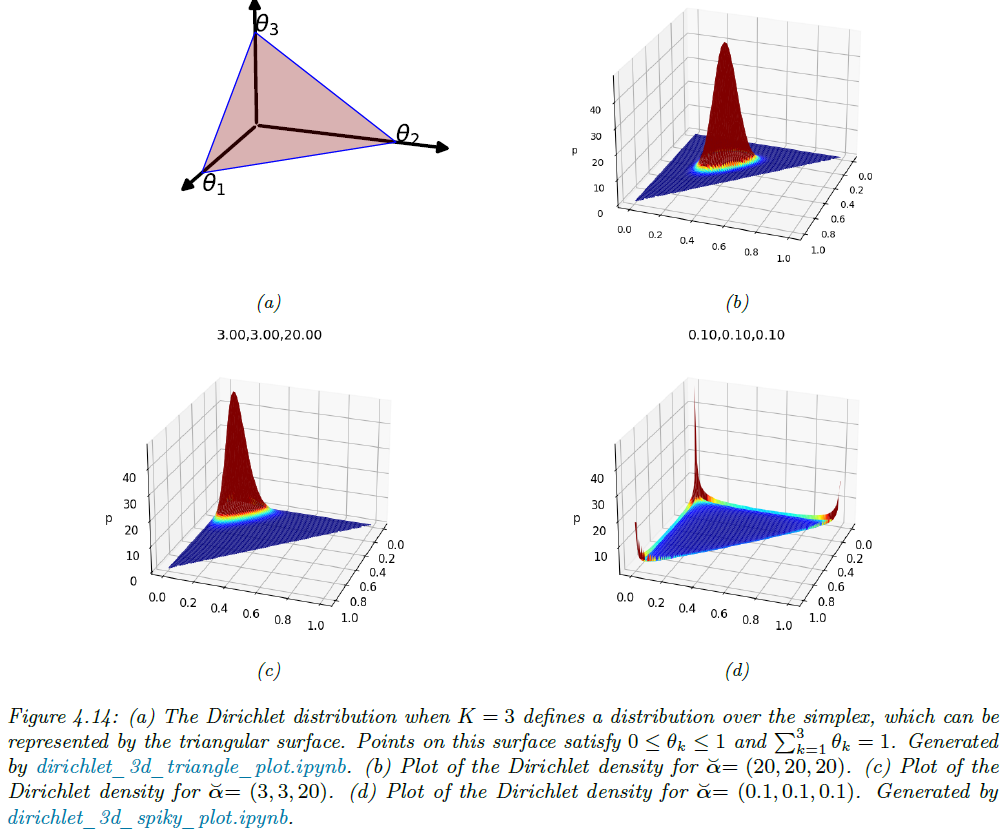
일단 $\alpha$라는 값의 직관적인 의미를 보도록 하죠. 그림 4.14를 보시면 더욱 쉽게 이해할 수 있습니다. $\alpha_{0} = \sum_{k = 1}^{K} \alpha_{k}$는 값이 클수록 분포가 뾰족해주고 작을수록 평평해지는 효과를 부여합니다. 그리고 각 $\alpha_{k}$는 분포가 어디에 집중되는 지 결정하죠. 예를 들어봅시다. $\text{Dir}(1, 1, 1)$은 완전 균일한 균등분포로 $\text{Beta}(1, 1)$의 삼차원 버전이라고 볼 수 있습니다. 그리고 $\text{Dir}(3, 3, 20)$은 한 범주에 치우친 비대칭 형태가 됩니다. 그리고 $\alpha_{k} < 1$이라면 꼭지점에 강한 가중치를 부여하여 샘플이 희소해지죠.
결론적으로 디리클레 분포는 베타 분포의 다변량 확장으로, 범주형 분포의 사전으로 이상적입니다. 그리고 하이퍼파라미터 $\mathbf{\alpha}$에서 $\alpha_{0}$는 신뢰수준을 의미하고 $\alpha_{k}$는 각 방향의 기대비율을 의미하죠. 이 구조 덕분에, 데이터 관측 후에도 사후분포가 디리클레 형태로 남아 계산이 간단해집니다.
3. 사후 분포(Posterior)
이전에 살펴본 다항 우도와 디리클레 사전확률분포를 곱해서 사후 확률분포를 구할 수 있습니다.
$$\begin{align} p(\mathbf{\theta} \mid \mathcal{D}) &\propto p(\mathcal{D} \mid \mathbf{\theta}) p(\mathbf{\theta}) \\ &= \left[ \prod_{k = 1}^{K} \theta_{k}^{N_{k}} \right] \left[ \prod_{k = 1}^{K} \theta_{k}^{\alpha_{k} - 1} \right] \\ &= \text{Dir} (\mathbf{\theta} \mid \alpha_{1} + N_{1}, \dots, \alpha_{K} + N_{K}) \\ &= \text{Dir}(\mathbf{\theta} \mid \hat{\mathbf{\alpha}}) \end{align}$$
여기서 $\hat{\alpha}_{k} = \alpha_{k} + N_{k}$로 “사전 카운트”에 “실제 관측 카운트”를 그대로 더하기만 하면 사후분포가 얻어집니다. 이제 사후 평균 $\mathbb{E}[\theta \mid \mathcal{D}]$을 구해보면 다음과 같습니다.
$$\mathbb{E}[\mathbf{\theta} \mid \mathcal{D}] = \frac{\hat{\alpha}_{k}}{\sum_{k^{'} = 1}^{K} \hat{\alpha}_{k^{'}}}$$
이는 사전 정보와 데이터가 모두 반영된 베이지안 추정값입니다. 다음으로 사후분포의 모드를 계산해보도록 하죠.
$$\hat{\theta}_{k}^{\text{MAP}} = \frac{\hat{\alpha}_{k} - 1}{\sum_{k^{'} = 1}^{K} (\hat{\alpha}_{k^{'}} - 1)}$$
이는 $\hat{\alpha}_{k} > 1$일 때 유효한 결과이며 MAP 추정에 해당하는 결과입니다. 만약, 모든 $k$에 대해서 $\alpha_{k} = 1$이라고 하면 이는 $\hat{\theta}_{k}^{\text{MAP}} = \frac{N_{k}}{N}$이 되는데 이는 MLE 추정과 일치합니다. “사전 정보가 전혀 없다”고 가정하면 베이즈 추정이 곧 빈도주의 추정이 되는 모습을 보여 줍니다. 이는 이전 포스팅과 유사한 결과를 주죠.
4. 사후 예측분포(Posterior Predictive)
베이즈 모델을 쓰는 궁극적 목적은 새로운 데이터가 들어왔을 때의 확률을 계산하는 것입니다. 이미 관측한 데이터셋 $\mathcal{D}$가 주어져있을 때 다음에 나올 범주 $y = k$를 구할 확률은 다음과 같이 얻습니다.
$$\begin{align} p(y = k \mid \mathcal{D}) &= \int p(y = k \mid \mathbf{\theta}) p(\mathbf{\theta} \mid \mathcal{D}) \; d\theta \\ &= \int \theta_{k}p(\mathbf{\theta} \mid \mathcal{D}) \; d\theta \\ &= \mathbb{E} [\theta_{k} \mid \mathcal{D}] \\ &= \frac{\hat{\alpha}_{k}}{\sum_{k^{'} = 1}^{K} \hat{\alpha}_{k}} \end{align}$$
결국 사후 예측분포의 형태는 $p(y \mid \mathcal{D}) = \text{Cat}(y \mid \mathbf{\theta})$라고 할 수 있습니다. 여기서 $\mathbf{\theta} = \mathbb{E}[\theta \mid \mathcal{D}]$이죠. 즉, 파라미터만 사후 평균으로 교체하면 됩니다.
5. 주변 우도(Marginal Likelihood)
디리클레-범주형 모델의 주변 우도는 베타–베르누이 사례와 동일한 방식으로 구할 수 있습니다.
$$p(\mathcal{D}) = \frac{B(\mathbf{N} + \mathbf{\alpha})}{ B(\mathbf{\alpha}) }$$
여기서 $\mathbf{N} = (N_{1}, \dots, N_{K})$는 각 범주가 관측된 횟수이고 $\mathbf{\alpha} = (\alpha_{1}, \dots, \alpha_{K})$는 사전 디리클레 하이퍼파라미터를 의미합니다. 여기서 $B(\alpha) = \frac{\prod_{k = 1}^{K} \Gamma (\alpha_{k})}{\Gamma (\sum_{k = 1}^{K} \alpha_{k})}$입니다. 심플하게 말해, 디리클레 분포의 정규화 상수입니다. 주변 우도식을 감마함수만으로 풀어서 쓰면 다음과 같습니다.
$$\begin{align} p(\mathcal{D}) &= \frac{\Gamma (\sum_{k = 1}^{K} \alpha_{k})}{\Gamma (N + \sum_{k = 1}^{K} \alpha_{k})} \prod_{k = 1}^{K} \frac{\Gamma (N_{k} + \alpha_{k})}{\Gamma (\alpha_{k})} \end{align}$$
각 범주 $k$다 “사전 + 데이터 카운트”가 감마 함수에 들어갑니다. 이 결과는 사전 정보와 관측 데이터를 하나로 합쳐 “바뀐 정규화 상수” 비율만 취하면 모델이 데이터를 얼마나 잘 설명하는지를 얻을 수 있습니다.
'인공지능 > Probabilistic Machine Learning (intro)' 카테고리의 다른 글
| [PML intro] Ch4 Statistics (Sec4.6 Bayesian Statistics - 5) (0) | 2025.07.22 |
|---|---|
| [PML intro] Ch4 Statistics (Sec4.6 Bayesian Statistics - 4) (0) | 2025.07.19 |
| [PML intro] Ch4 Statistics (Sec4.6 Bayesian Statistics - 2) (1) | 2025.07.17 |
| [PML intro] Ch4 Statistics (Sec4.6 Bayesian Statistics - 1) (3) | 2025.07.16 |
| [PML intro] Ch4 Statistics (Sec4.5 Regularization - 4) (0) | 2025.07.15 |
