안녕하세요. 지난 포스팅에서는 디리클레-멀티모달 모델을 이용해서 베이지안 통계를 배워보았습니다. 이번에는 가우시안 평균 $\mu$에 대한 사후분포를 유도해보는 과정을 알아보겠습니다. 여기서는 계산을 단순하게 하기 위해 분산 $\sigma^{2}$는 이미 알려져 있다고 가정하겠습니다. 분산까지 함께 추정하는 더 일반적인 경우는 향후에 더 자세히 알아보도록 하겠습니다.
일단 데이터셋 $\mathcal{D} = \{ y_{1}, \dots, y_{N} \}$이 주어진다고 가정하면 $\mu$에 대한 가우시안 함수의 우도함수는 다음과 같은 형태를 지니게 됩니다.
$$p(\mathcal{D} \mid \mu) \propto \text{exp} \left( -\frac{1}{2\sigma^{2}} \sum_{n = 1}^{N} (y_{n} - \mu)^{2} \right)$$
가우시안 분포가 베이지안 통계에 있어서 중요한 이유 중 하나는 가우시안 분포의 공액 사전 확률분포 역시 가우시안 이기 때문입니다. 따라서, 사전 확률분포 역시 가우시안이라고 가정하면 $p(\mu) = \mathcal{N} (\mu \mid \tilde{m}, \tilde{\tau}^{2})$라고 쓸 수 있습니다.
다음 단계는 뻔하죠. 베이즈 정리를 이용하여 사후 확률분포를 구하면 됩니다.
$$\begin{cases} p(\mu \mid \mathcal{D}, \sigma^{2}) &= \mathcal{N}(\mu \mid \hat{m}, \hat{\tau}^{2}) \\ \hat{\tau}^{2} & = \left( \frac{N}{\sigma^{2}} + \frac{1}{\tilde{\tau}^{2}} \right)^{-1} = \frac{\sigma^{2}\tilde{\tau}^{2}}{N\tilde{\tau}^{2} + \sigma^{2}} \\ \hat{m} &= \hat{\tau}^{2} \left( \frac{\tilde{m}}{\tilde{\tau}^{2}} + \frac{N\bar{y}}{\sigma^{2}} \right) = \frac{\sigma^{2}}{N\tilde{\tau}^{2} + \sigma^{2}} \tilde{m} + \frac{N\tilde{\tau}^{2}}{N\tilde{\tau}^{2} + \sigma^{2}}\bar{y} \end{cases}$$
여기서 $\bar{y} = \frac{1}{N}\sum_{n = 1}^{N} y_{n}$은 표본평균으로 정의됩니다. 다음에는 정밀도 관점에서 사후 확률분포를 정의해보도록 하겠습니다. 즉, $\kappa = \frac{1}{\sigma^{2}}$을 관측 정밀도, 그리고 $\tilde{\lambda} =\frac{1}{\tilde{\tau}^{2}}$을 사전 정밀도라고 가정하겠습니다. 그리고 이를 사후 확률분포에 적용하여 다시 쓰면 다음과 같이 쓸 수 있습니다.
$$\begin{cases} p(\mu \mid \mathcal{D}, \kappa) &= \mathcal{N}(\mu \mid \hat{m}, \tilde{\lambda}^{-1}) \\ \hat{\lambda} & = \tilde{\lambda} + N \kappa \\ \hat{m} &= \frac{N \kappa \bar{y} + \tilde{\lambda} \tilde{m}}{\hat{\lambda}} = \frac{N \kappa}{N \kappa + \tilde{\lambda}} \bar{y} + \frac{\tilde{\lambda}}{N \kappa + \tilde{\lambda}} \tilde{m} \end{cases}$$
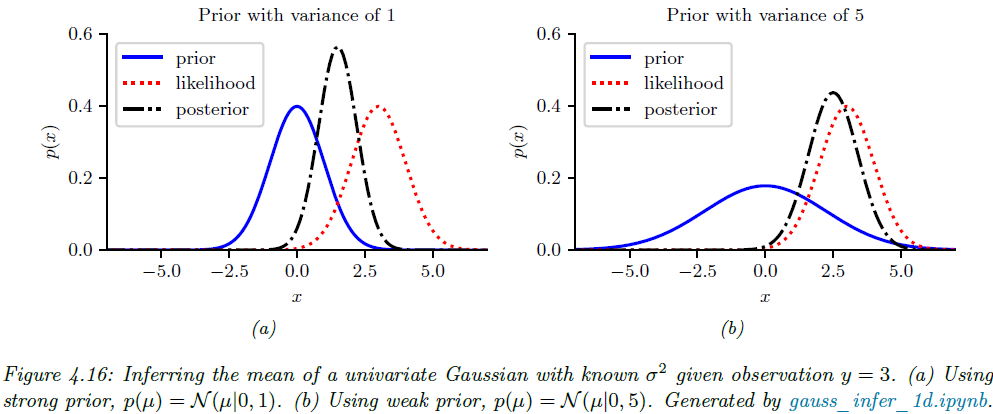
여기서 $\hat{\lambda} = \tilde{\lambda} + N\kappa$는 사후 정밀도로 사전의 확신(정밀도)에 측정 $N$회가 주는 정밀도 $N\kappa$가 더해집니다. 그리고 $\hat{m}$은 사후 평균으로 표본 평균 $\bar{y}$와 사전 평균 $\tilde{m}$의 가중 평균(볼록 결합)으로 구성되있습니다. 따라서 사전 정보가 약하다면 데이터 쪽 가중치가 커져서 $\hat{m} \approx \bar{y}$가 되고 반대로 사전 정보가 강하다면 사전을 더 신뢰하게 되어 $\hat{m} \approx \tilde{m}$이 됩니다. 이 전체적인 요약은 그림 4.16에서도 볼 수 있습니다.
이번에는 $N = 1$인 경우의 사후 확률분포를 분석해보도록 하겠습니다. 즉, 데이터가 한점 $y$만 주어진 것이겠죠? 이 경우에 사후 평균 $\hat{m}$은 다음과 같이 표현될 수 있습니다.
$$\begin{cases} \hat{m} &= \frac{\tilde{\lambda}}{\hat{\lambda}} \tilde{m} + \frac{\kappa}{\hat{\lambda}} y \\ \hat{m} &= \tilde{m} + \frac{\kappa}{\hat{\lambda}} (y - \tilde{m}) \\ \hat{m} &= y - \frac{\kappa}{\hat{\lambda}} (y - \tilde{m}) \end{cases}$$
첫번째 식은 사전 평균 $\tilde{m}$과 데이터 $y$ 사이의 두 가중치 $ \frac{\tilde{\lambda}}{\hat{\lambda}} $와 $ \frac{\kappa}{\hat{\lambda}} $에 의한 볼록 결합으로 정의됩니다.
두번째 식은 사전 평균 $\tilde{m}$을 데이터쪽으로 이동시키며 이동량은 $\frac{\kappa}{\hat{\lambda}} \times (y - \tilde{m})$만큼이 됩니다. 즉, 관측정밀도와 사후 정밀도 사이의 비율에 관측 데이터와 사전 평균 사이의 오차만큼 이동하게 됩니다.
세번째 식은 데이터 $y$를 사전 평균쪽으로 수축(Shrink)한다고 합니다. 이를 “수축 추정(shrinkage estimate)”이라고 부르죠.
아직은 조금 어려운 거 같으니 조금 더 쉽게 해석해보기 위해 $w = \frac{\tilde{\lambda}}{\hat{\lambda}}$라고 두겠습니다. 그러면 $0 \le w \le 1$이 됩니다. 그리고 이를 이용하면 다음과 같이 식을 바꿀 수 있죠.
$$\hat{m} = y - w (y - \tilde{m}) = (1 - w) y + w\tilde{m}$$
즉, $w$는 “사전 정보의 힘(정밀도)”이 사후에 차지하는 비율이고 $1 - w$는 데이터 한 점이 차지하는 비율을 의미합니다. 따라서, 사전이 약하다는 것은 $\tilde{\lambda} < \kappa$이기 때문에 $w \approx 0$이 되어 $\hat{m} \approx y$가 되는 것이죠. 반대로 사전이 크다는 것은 $\tilde{\lambda} > \kappa$이기 때문에 $w \approx 1$이 되어 $\hat{m} \approx \tilde{m}$가 되는 것이죠.
또한, 정규분포에서는 사후 평균 = 사후 모드이므로, 위 식들은 그대로 MAP 추정 공식을 제공합니다. 하나씩 풀어보도록 하죠. 일단 문제 정의부터 해보면 관측치는 $\mathcal{D} = \{ y_{1}, \dots, y_{N} \}$이라고 하겠습니다. 그리고 모델로 $y_{n} \mid \mu \sim \mathcal{N}(\mu, \sigma^{2})$이라고 하겠습니다. 여기서는 분산인 $\sigma^{2}$은 알고 있다고 가정하겠습니다. 그리고 사전 정보는 $\mu \sim \mathcal{N}(\tilde{m}, \tilde{\tau}^{2})$이라고 하겠습니다.
이때, 정밀도를 쓰면 계산이 더 간결해지기 때문에 관측정밀도 $\kappa = \frac{1}{\sigma^{2}}$과 사전정밀도 $\tilde{\lambda} = \frac{1}{\tilde{\tau}^{2}}$이라고 두겠습니다. 지금까지 MAP 구하는 과정을 많이 보았지만 다시 상기해보자면 다음과 같은 식을 최적화하면 됩니다.
$$\mu_{\text{MAP}} = \text{argmax}_{\mu} p(\mu \mid y) = \text{argmax}_{\mu} \left[ \log p(\mathbf{y} \mid \mu) + \log p(\mu) \right]$$
먼저, 관측된 데이터에 대한 I.I.D 가정을 하고 가우시안 로그 우도 $\log p(\mathbf{y} \mid \mu)$ 를 구해보도록 하겠습니다.
$$\begin{align} &p(\mathcal{D} \mid \mu) = \prod_{n = 1}^{N} \frac{1}{\sqrt{2\pi\sigma^{2}}} \text{exp} \left[ -\frac{1}{-2\sigma^{2}} (y_{n} - \mu)^{2} \right] \\ \Rightarrow& \log p(\mathbf{y} \mid \mu) = \sum_{n = 1}^{N} \left[ -\frac{1}{2} \log (2\pi\sigma^{2}) - \frac{1}{2\sigma^{2}} (y_{n} - \mu)^{2} \right] \\ &= -\frac{N}{2} \log(2\pi\sigma^{2}) - \frac{1}{2\sigma^{2}} \sum_{n = 1}^{N} (y_{n} - \mu)^{2} \\ &= -\frac{N}{2} \log (2\pi\sigma^{2}) - \frac{\kappa}{2} \sum_{n = 1}^{N} (y_{n} - \mu)^{2} \end{align}$$
다음으로, 가우시안에 대한 로그 사전 확률분포 $p(\mu) \sim \mathcal{N}(\mu \mid \tilde{\mu}, \tilde{\tau}^{2})$를 구해보도록 하겠습니다.
$$\begin{align} &p(\mu) = \frac{1}{\sqrt{2\pi\sigma^{2}}} \text{exp} \left[ -\frac{1}{2\sigma^{2}} (\mu - \tilde{\mu}) \right] \\ \Rightarrow& \log p(\mu) = \log \left[ \frac{1}{\sqrt{2\pi\tilde{\tau}^{2}}} \right] + \log \left[ \text{exp} \left( -\frac{1}{\tilde{\tau}^{2}} (\mu - \tilde{m})^{2} \right) \right] \\ &= -\frac{1}{2} \log (2\pi \tilde{\tau}^{2}) - \frac{1}{2\tilde{\tau}^{2}} (\mu - \tilde{m})^{2} \\ &= -\frac{1}{2} \log (2\pi\tilde{\tau}^{2}) - \frac{\tilde{\lambda}}{2} (\mu - \tilde{m})^{2} \end{align}$$
여기서 $\log p(\mathbf{y} \mid \mu)$와 $\log p(\mu)$는 각각 로그 우도와 로그 사전 확률분포로 가우시안 분포와 I.I.D를 가정하기 때문에 다음과 같이 쓸 수 있습니다.
$$\begin{cases} \log p(\mathbf{y} \mid \mu) &= -\frac{N}{2} \log (2\pi\sigma^{2}) - \frac{\kappa}{2} \sum_{n = 1}^{N} (y_{n} - \mu)^{2} \\ \log p(\mu) &= -\frac{1}{2} \log (2\pi \tilde{\tau}^{2}) - \frac{\tilde{\lambda}}{2} (\mu - \tilde{m})^{2} \end{cases}$$
이제 위 두 식을 결합해서 $\mu$에 대한 식으로 모으면 다음과 같습니다.
$$-\frac{1}{2} \left[ (N \kappa + \tilde{\lambda})\mu^{2} - 2(N\kappa \bar{y} + \tilde{\lambda} \tilde{m})\mu \right] + \text{const}$$
여기서, $\bar{y} = \frac{1}{N} \sum_{n = 1}^{N} y_{n}$은 표본평균이고 $\text{const}$는 $\mu$와 관련없는 항을 의미합니다. 이제 이차식 최대화를 통해 $\mu_{\text{MAP}}$를 유도할 수 있습니다.
$$\mu_{\text{MAP}} = \frac{N\kappa\bar{y} + \tilde{\lambda}\tilde{m}}{N\kappa + \tilde{\lambda}} = \frac{N\kappa}{N\kappa + \tilde{y}} \bar{y} + \frac{\tilde{y}}{N\kappa + \tilde{\lambda}}\tilde{m}$$
이는 저희가 구한 사후평균과 동일한 결과를 주게됩니다. 즉, 가우시안–가우시안에서 사후평균 = MAP 추정치임을 확인한 것이죠. 마지막은 사후 분산과 표준 오차(Standard Error of Mean; SEM)을 구해보도록 하겠습니다. 가우시안-가우시안 모형에서 사후 확률분포는 다음과 같이 쓸 수 있습니다.
$$\begin{cases} p(\mu \mid \mathcal{D}) &= \mathcal{N}(\mu \mid \hat{\mu}, \hat{\lambda}^{-1}) \\ \hat{\lambda} &= \lambda + N\kappa \end{cases}$$
따라서, $\mathbb{V}[\mu \mid \mathcal{D}] = \hat{\lambda}^{-1}$이고 SEM은 $\text{se}(\mu) = \sqrt{\mathbb{V}[\mu \mid \mathcal{D}]} = \frac{1}{\hat{\lambda}} = \hat{\lambda}^{-\frac{1}{2}}$가 됩니다. 여기서 사전 정보가 의미없다고 가정하면 $\lambda = 0$이 되고 사후 정보는 $\hat{\lambda} = N\kappa = \frac{N}{\sigma^{2}}$이 되겠죠. 결론적으로 $\mathbb{V}[\mu \mid \mathcal{D}]$와 $\text{se}(\mu)$는 다음과 같이 쓸 수 있죠.
$$\begin{cases} \mathbb{V}[\mu \mid \mathcal{D}] &= \frac{\sigma^{2}}{N} \\ \text{se}(\mu) &= \frac{\sigma}{\sqrt{N}} \end{cases}$$
여기서 데이터가 늘어날수록 분산은 $\frac{1}{N}$ 속도로 감소하여 표준 오차는 $\frac{1}{\sqrt{N}}$만큼 비례에서 감소하게 됩니다. 물론 이 경우에는 $\sigma$를 알고 있다고 가정했기 때문에 모르는 경우에는 표본 분산 $s^{2} = \frac{1}{N} \sum_{n = 1}^{N} (y_{n} - \bar{y})^{2}$을 이용해서 근사하게 됩니다. 따라서, $\hat{\kappa} = \frac{1}{s^{2}}$이 되고 $\hat{\lambda} = N\hat{\kappa} = \frac{N}{s^{2}}$이 되죠. 이를 최종식에 다시 대입하면 다음과 같이 동일하게 쓸 수 있습니다.
$$\begin{cases} \mathbb{V}[\mu \mid \mathcal{D}] &= \frac{s^{2}}{N} \\ \text{se}(\mu) &= \frac{s}{\sqrt{N}} \end{cases}$$
마지막으로 일반적으로 가우시안 분포의 $\pm 2\sigma$가 약 95%를 커버하기 때문에 $I_{0.95}(\mu \mid \mathcal{D}) \approx \bar{y} \pm 2 \text{se}(\mu) = \bar{y} \pm 2 \frac{s}{\sqrt{N}}$이 됩니다.
'인공지능 > Probabilistic Machine Learning (intro)' 카테고리의 다른 글
| [PML intro] Ch4 Statistics (Sec4.6 Bayesian Statistics - 6) (0) | 2025.07.22 |
|---|---|
| [PML intro] Ch4 Statistics (Sec4.6 Bayesian Statistics - 5) (0) | 2025.07.22 |
| [PML intro] Ch4 Statistics (Sec4.6 Bayesian Statistics - 3) (2) | 2025.07.18 |
| [PML intro] Ch4 Statistics (Sec4.6 Bayesian Statistics - 2) (1) | 2025.07.17 |
| [PML intro] Ch4 Statistics (Sec4.6 Bayesian Statistics - 1) (3) | 2025.07.16 |
