안녕하세요. 지난 포스팅의 [IS2D] RefineNet: Multi-Path Refinement Networks for High Resolution Semantic Segmentation (CVPR2017)에서는 RCU, MRF, CRP로 구성된 RefineNet에 대해서 알아보았습니다. 이를 통해 고해상도의 영상에서도 높은 성능을 달성하게 되었죠. 오늘은 self-attention의 확장된 개념인 Non-local Operation을 활용하여 설계한 Non-local Neural Network에 대해서 알아보도록 하겠습니다.
Background
최근 음성, 신호, 자연어와 같은 시퀀셜 데이터 (Sequential Data)를 다루는 분야에서 recurrent operation을 활용하여 데이터에 내재된 long-range dependency를 모델링하는 방법이 인기가 많아지고 있습니다. 컴퓨터 비전 분야에서는 더욱 깊게 쌓은 convolution operation을 활용하여 receptive field를 늘림으로써 long-range dependency를 모델링하게 되죠.
하지만 근본적으로 recurrent / convolution operation은 모두 space, time 또는 space-time에 대한 local neighborhood를 처리하게 됩니다. 따라서, 굉장히 긴 시퀀스 또는 고해상도의 영상이 입력되면 이러한 연산을 더욱 많이 반복해야하기 때문에 비효율적이고 파라미터의 개수나 FLOPs가 증가하여 최적화가 어려워지는 문제점이 발생하곤 합니다.
따라서 본 논문에서는 이러한 한계점을 극복하기 위한 non-local operation을 제안합니다. 이는 효율적 (efficient)이며 간단 (simple)하고 일반적 (generic)으로 사용될 수 있는 모듈로써 단 한번의 연산으로 아래 그림과 같이 영상, 비디오, 시퀀스에 관계없이 long-range dependency를 얻을 수 있다는 장정이 있습니다. 이러한 연산으로 기반으로 본 논문에서는 Non-local Neural Network를 제안하였으며 이는 Video Classification, Semantic Segmentation, Keypoint Detection에서 보다 높은 성능을 달성하였습니다.

Non-local Neural Networks
1) Formulation
일단 Non-local operation은 훨씬 이전에 나왔던 영상 복원을 위해 제안된 Non-local mean operation을 기반으로 설계되었습니다. 이를 generic한 non-local operation으로 사용하기 위해 저희는 다음과 같이 공식화하여 작성할 수 있습니다.
$$\mathbf{y}_{i} = \frac{1}{\mathcal{C}(\mathbf{x})} \sum_{\forall j} f(\mathbf{x}_{i}, \mathbf{x}_{j}) g(\mathbf{x}_{j}) $$
여기서 $i$는 출력 위치 (space, time 또는 space-time)의 인덱스, $j$는 모든 가능한 위치들을 의미합니다. 따라서, 하나의 출력 위치를 얻기 위해서는 모든 위치들에 대한 정보를 활용해야하기 때문에 위 수식은 long-range dependency를 얻을 수 있게 되는 것이죠. 그리고 $\mathbf{x}$는 입력 데이터로 영상, 비디오, 시퀀스, 특징 맵 등 아무거나 될 수 있습니다.
이때 중요한 것은 이항 연산인 $f(\mathbf{x}_{i}, \mathbf{x}_{j})$로 이는 서로 다른 두 위치 $i$와 $j$ 간의 관계를 모델링하여 하나의 스칼라 값으로 만들어주는 함수입니다. 핵심은 $f(\mathbf{x}_{i}, \mathbf{x}_{j})$을 어떻게 정의하느냐에 따라 두 위치 간의 관계성이 달라지게 될 것 입니다. 다음으로 단항 연산인 $g(\mathbf{x}_{j})$는 $j$ 위치에 대한 입력 신호를 임베딩하는 방식을 의미합니다. 마지막으로 $\mathcal{C}(\mathbf{x})$는 정규화를 위한 요소입니다.
위와 같이 정의된 non-local operation과 convolution 및 recurrent operation의 차이점은 한번의 연산으로 long-range dependency를 얻을 수 있다는 점 입니다. convolution operation의 경우 위 연산에서 $i - 1 \le j \le i + 1$이고 recurrent operation의 경우 $j = i - 1$이거나 $j = i$입니다. 두 연산 모두 한번의 연산으로는 neighborhood 정보만을 고려하는 것을 볼 수 있죠.
물론 non-local operation은 fully-connected layer와도 서로 다른 특징을 보이게 됩니다. non-local operation은 서로 다른 위치 간의 관계성을 모델링하지만 fully-connected layer은 학습된 가중치를 이용하여 모델링하죠. 이는 fully-connected layer에서는 서로 다른 위치 $\mathbf{x}_{i}$와 $\mathbf{x}_{j}$ 사이의 관계는 함수로써 정의되지 않는 다는 것을 의미합니다. 또한, fully-connected layer는 고정된 입력 데이터만 다룰 수 있지만 non-local operation는 임의의 길이를 가진 데이터가 들어오더라도 처리할 수 있습니다.
이러한 non-local operation의 장점을 이용하여 non-local & local operation을 함께 활용할 수 있기 때문에 이전 방법들보다 더 풍부하고 계층적인 정보를 추출하여 모델의 표현력을 향상시킬 수 있게 됩니다.
2) Instantiations
본 논문에서는 $f(\mathbf{x}_{i}, \mathbf{x}_{j})$의 정의에 따라 다양한 non-local operation을 제시합니다. 다만, 결과적으로 $f(\mathbf{x}_{i}, \mathbf{x}_{j})$에 따라서 그렇게 성능이 크게 차이나지는 않는 다고 합니다. 여기서, 단순함을 위해 $g(\mathbf{x}_{j}) = W_{g}\mathbf{x}_{j}$로 단일 계층의 임베딩 함수 ($1 \times 1$ convolution)로 고정하도록 하겠습니다.
- Gaussian: $f(\mathbf{x}_{i}, \mathbf{x}_{j}) = e^{\mathbf{x}_{i}^{T} \mathbf{x}_{j}}$
- Embedded Gaussian: $f(\mathbf{x}_{i}, \mathbf{x}_{j}) = e^{\theta (\mathbf{x}_{i})^{T} \phi(\mathbf{x}_{j})}$
- Dot Product: $f(\mathbf{x}_{i}, \mathbf{x}_{j}) = \theta (\mathbf{x}_{i})^{T} \phi(\mathbf{x}_{j})$
- Concatenation: $f(\mathbf{x}_{i}, \mathbf{x}_{j}) = \text{ReLU} (\mathbf{w}_{f}^{T} [\theta (\mathbf{x}_{i}), \phi (\mathbf{x}_{j})])$
흔히 Transformer 이후에 크게 대두된 Self-Attention은 Embedded Gaussian의 special case function이라고 보시면 될 거 같습니다.
- Self-Attention: $\mathbf{y} = \textbf{Softmax} (\mathbf{x}^{T} W_{\theta}^{T} W_{\phi} \mathbf{x}) g(\mathbf{x})$
재밌는 점은 일반적인 non-local operation과 다르게 Self-Attention은 말그대로 자기자신 (Self)에 대한 각 위치의 중요도를 측정하는 방식으로 long-range dependency를 모델링하게 되죠.
3) Non-local Block
$$\mathbf{z}_{i} = W_{z}\mathbf{y}_{i} + \mathbf{x}_{i}$$
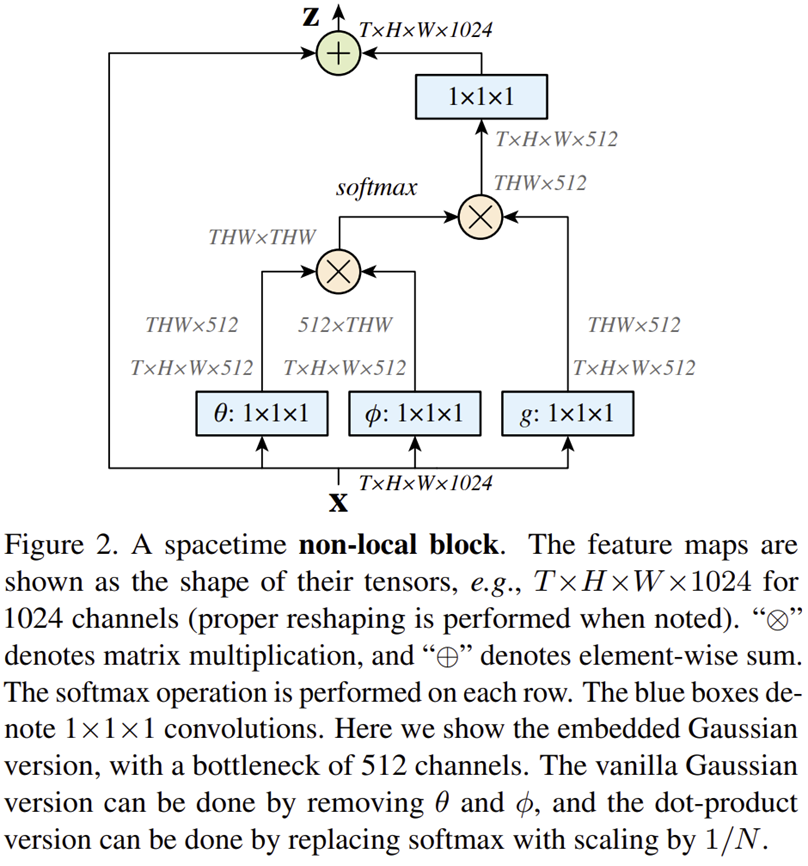
최종적으로 본 논문에서는 그림 2와 위 수식과 같은 형태의 Non-local Block을 제안하여 이를 모델에 적용하게 됩니다. 참고로 이러한 형태의 연산이 나온 이후로 많은 모델들이 해당 설계를 따르게 되었습니다. 가장 대표적으로 [IC2D] Attentional Feature Fusion (WACV2021)이 그러하죠.
Video Classification Models

본 논문에서는 Video Classification에서의 성능을 먼저 확인하기 위해 표 1과 같이 단순한 모델을 설계합니다. 해당 모델은 기본적으로 ResNet50을 기반으로 만들었으며 입력 비디오 클립은 32 프레임씩 $224 \times 224$ 크기의 영상이 입력됩니다.
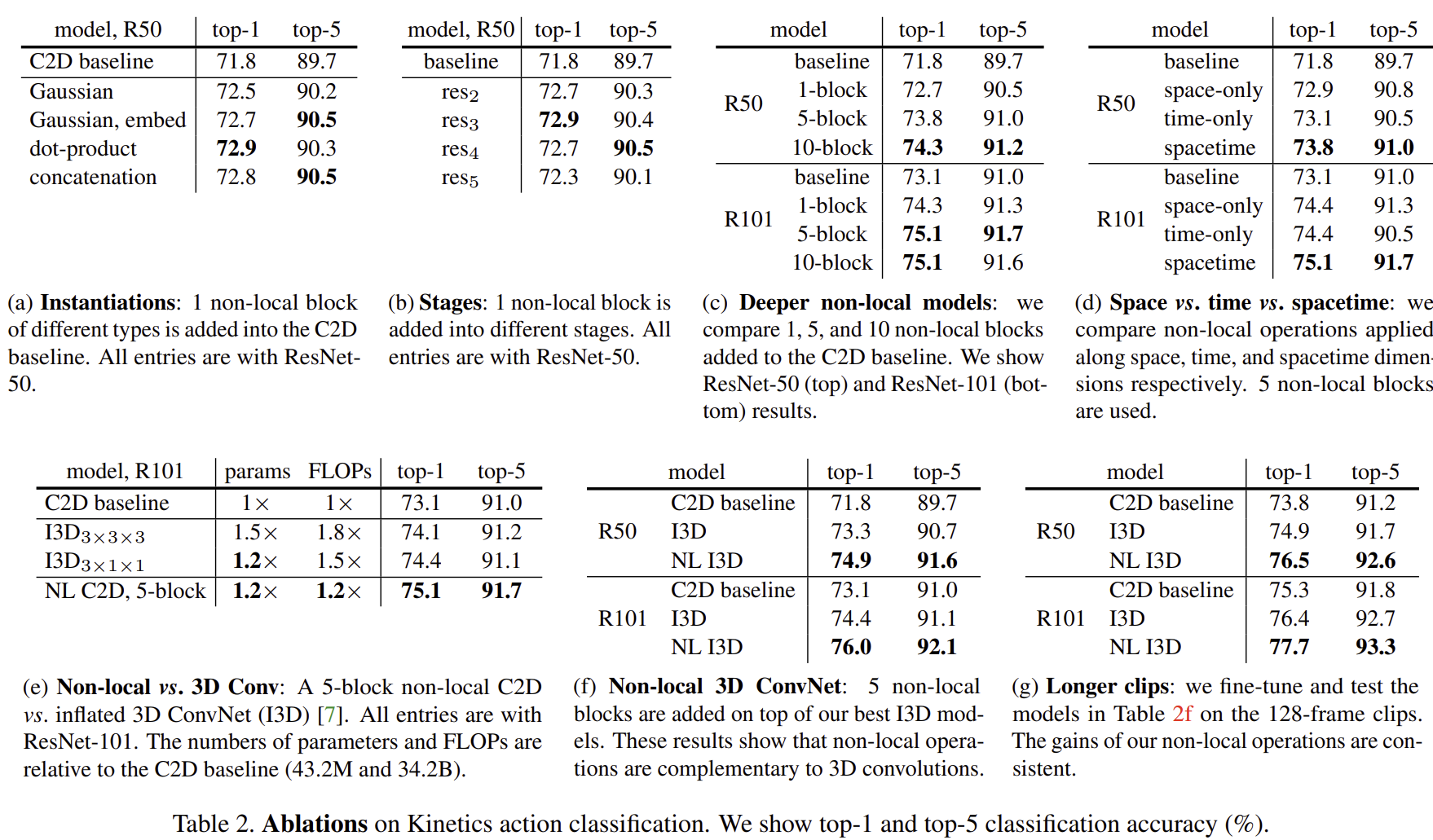
표 2는 본 논문에서 Video Classification 데이터셋인 Kinetic action classification dataset에서 수행한 ablation study입니다.
- (a)는 처음에 보았던 non-local operation의 $f(\mathbf{x}_{i}, \mathbf{x}_{j})$의 정의별 (Gaussian, Embedded Gaussian, Dot Product, Concatenation)에서의 성능 비교입니다. $f(\mathbf{x}_{i}, \mathbf{x}_{j})$의 종류에 따라 큰 성능 변화는 나타나지는 않지만 적어도 적용안했을 때 보다는 성능이 오르는 것을 볼 수 있습니다.
- (b)는 non-local operation을 어디에 적용할 지에 대한 성능 평가 결과 입니다. 이 역시 큰 성능 변화는 나타나지는 않지만 적어도 적용안했을 때 보다는 성능이 오르는 것을 볼 수 있습니다.
- (c)는 더 깊은 모델 (ResNet101)에서 non-local operation을 적용했을 때 실험 결과로 이 역시 더 높은 결과를 얻을 수 있습니다.
- (d)는 long-range dependency를 space, time, space&time에 대해서 얻었을 때 실험결과로 예상한대로 두 차원에 대한 long-range dependency를 얻어야 성능이 더 좋은 것을 볼 수 있습니다.
- (e)는 3D Convolution과 non-local operation 사이의 효율성에 대한 평가로 3D Convolution에 비해 더 적은 파라미터와 FLOPs로 더 높은 성능을 얻을수 있습니다.
- (f)는 non-local operation을 3D Convolution 모델에 적용했을 때 평가로 이 역시 성능이 크게 증가하는 것을 볼 수 있습니다.
- (g)는 본 논문에서 사용한 데이터셋이 Video 데이터셋이기 때문에 더 긴 시퀀스의 프레임이 입력되었을 때 long-range dependency를 잘 잡는다면 성능이 더 높을 것이라고 예상할 수 있습니다. 여기서는 128개의 프레임을 한번에 입력했을 때 결과로 성능이 더 좋아지는 것을 볼 수 있습니다.
위 ablation study의 결과에서 볼 수 있다싶이 non-local operation은 generic하게 2D/3D Convolution에 관계없이 어떠한 모델에서도 적용해볼 수 있으며 space-time long-range dependency를 잡을 때 성능이 가장 높게 나온다는 것을 알 수 있습니다. 이러한 실험에서 non-local operation은 더욱 긴 시퀀스 (128 프레임)에서도 space-time long-range dependency를 잘 잡아낸다는 사실을 알 수 있죠.
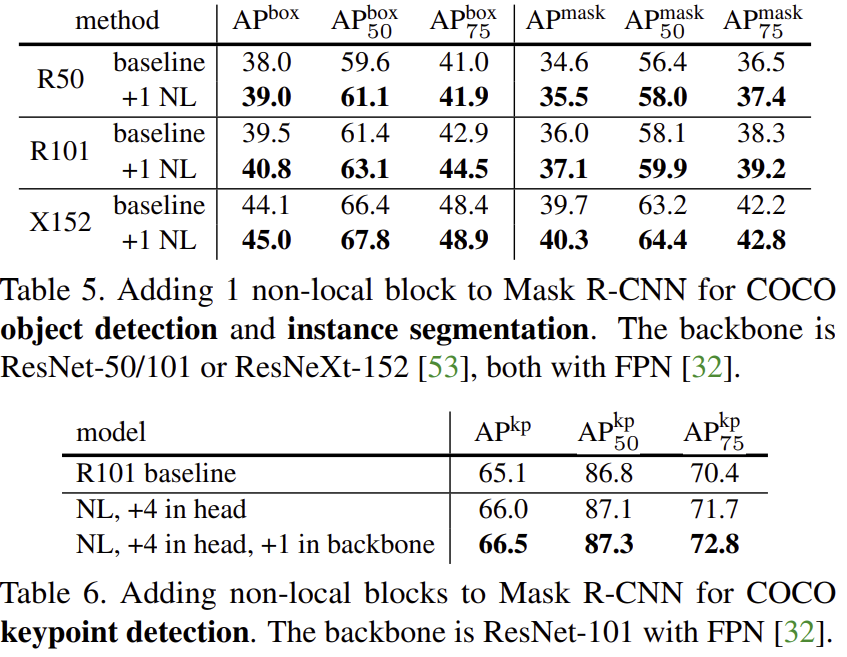
표 5와 표 6은 non-local operation을 적용했을 때 각각 COCO 데이터셋의 task인 object detection & instance segmentation & keypoint detection에 대한 성능을 측정한 결과로 이 역시 더 높은 결과를 얻을 수 있습니다.
