안녕하세요. 지난 포스팅의 [Transformer] An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale (ICLR2021)에서는 Vision Transformer (ViT)에 대해 소개해드렸습니다. 핵심은 기존의 NLP 분야에서 많이 사용되는 Transformer를 Computer Vision 분야에서도 활용하기 위해 입력 영상을 패치로 분해한 뒤 patch embedding과 positional encoding을 통해 1D sequence 데이터와 같이 이용할 수 있는 방법에 대해 제안하였습니다. 오늘은 ViT의 한계점을 지적하며 등장한 Swin Transformer에 대해 소개해드리도록 하겠습니다.
Swin Transformer: Hierarchical Vision Transformer using Shifted Windows
This paper presents a new vision Transformer, called Swin Transformer, that capably serves as a general-purpose backbone for computer vision. Challenges in adapting Transformer from language to vision arise from differences between the two domains, such as
arxiv.org
Background
Swin Transformer가 제안된 배경을 이해하기 위해서는 ViT에 대한 이해가 필수입니다. 지난 포스팅에서도 설명했지만, ViT에서는 Transformer 구조를 영상 인식 분야에 활용하기 위해 입력 영상을 패치 단위로 쪼개어 patch embedding 과정을 거쳐 1D sequence 데이터로 변형하여 사용하였습니다. 다음에는 Transformer가 적용되어 모든 패치 간의 self-attention을 수행하기 때문에 global context information을 얻을 수 있죠.
하지만, Language Domain과는 다르게 Visual Domain은 픽셀의 개수가 매우 자유자재로 변화할 수 있습니다. 예를 들어, $224 \times 224$ 크기가 아닌 $1024 \times 1024$와 같은 고해상도의 영상을 생각해보시면 됩니다. 그러면 ViT에서는 해당 영상도 작은 패치 단위로 쪼개어 연산을 수행하겠죠. 그런데 이는 해상도가 커지면 커질수록 패치의 개수가 많아져 self-attention 시 발생하는 복잡도에 큰 영향을 주게 됩니다. 이러한 문제는 ViT 구조를 그대로 Computer Vision 분야에 활용하기는 어렵게 만듭니다. 실제로 영상 크기의 제곱만큼 Transformer의 복잡도가 제곱수만 증가한다고 하네요.
그렇다면 이러한 문제가 발생하는 이유가 무엇일까요? ViT에서는 모든 Stage에서 고정된 크기의 패치를 사용하여 복잡도가 줄어들 수가 없는 것이죠. CNN에서도 합성곱 연산의 복잡도를 줄이기 위해 풀링 연산을 적용하여 영상의 크기를 절반으로 줄이는 과정을 볼 수 있습니다.
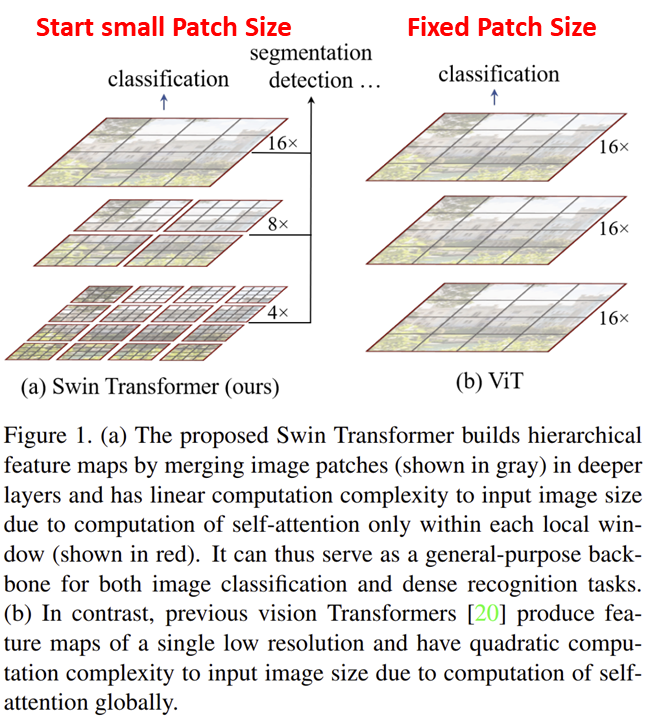
따라서, Swin Transformer는 그림 1과 같은 patch merging 방식을 제안합니다. 보시면 각 stage 별로 패치의 크기가 다른 것을 볼 수 있죠. 위 그림의 핵심은 Window (빨간색 상자) 내부의 패치에서만 self-attention을 수행한다는 점 입니다. 이를 통해, 작은 크기의 패치를 처음에 사용하여 점점 패치의 크기를 키움으로써 기존의 Transformer의 장점인 global context information도 함께 얻어낼 수 있습니다.
이를 통해, Swin Transformer는 Semantic Segmentation이나 Object Detection과 같은 Dense Prediction Task에서도 활용할 수 있게 되었습니다. 또한, ViT에서는 영상 크기의 제곱에 비례하여 self-attention의 복잡도가 증가하였습니다. Swin Transformer에서는 이러한 문제를 어느정도 완화시켜 선형적인 복잡도로 감소시켰습니다.
Method
1). Overall Architecture
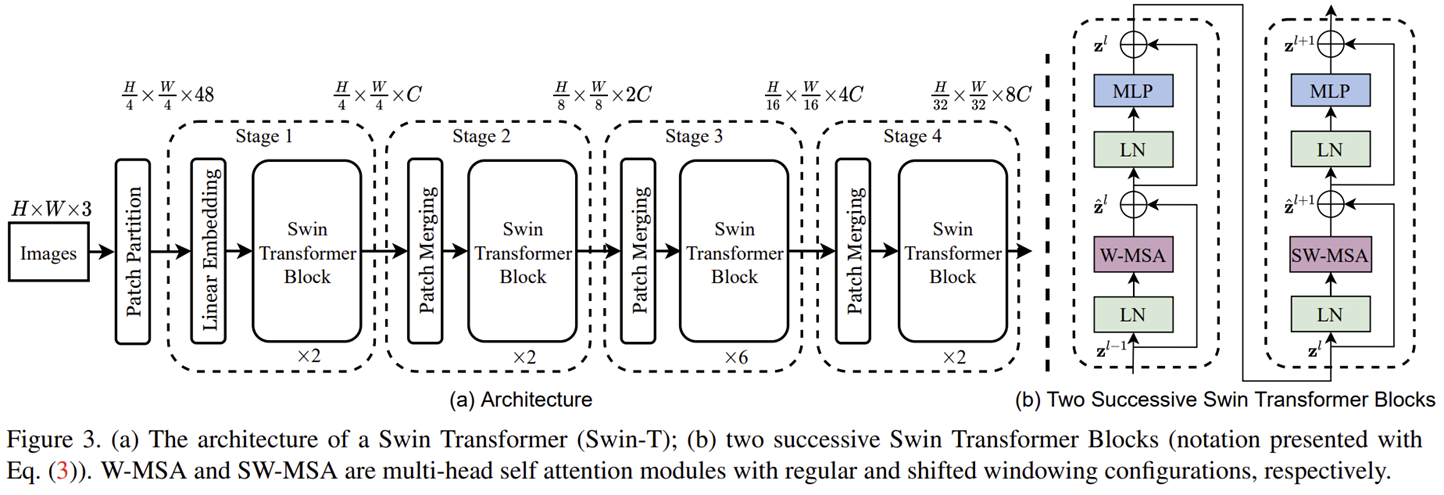
그림 3은 Swin-T (Tiny) 구조의 블록 다이어그램을 보여주고 있습니다.
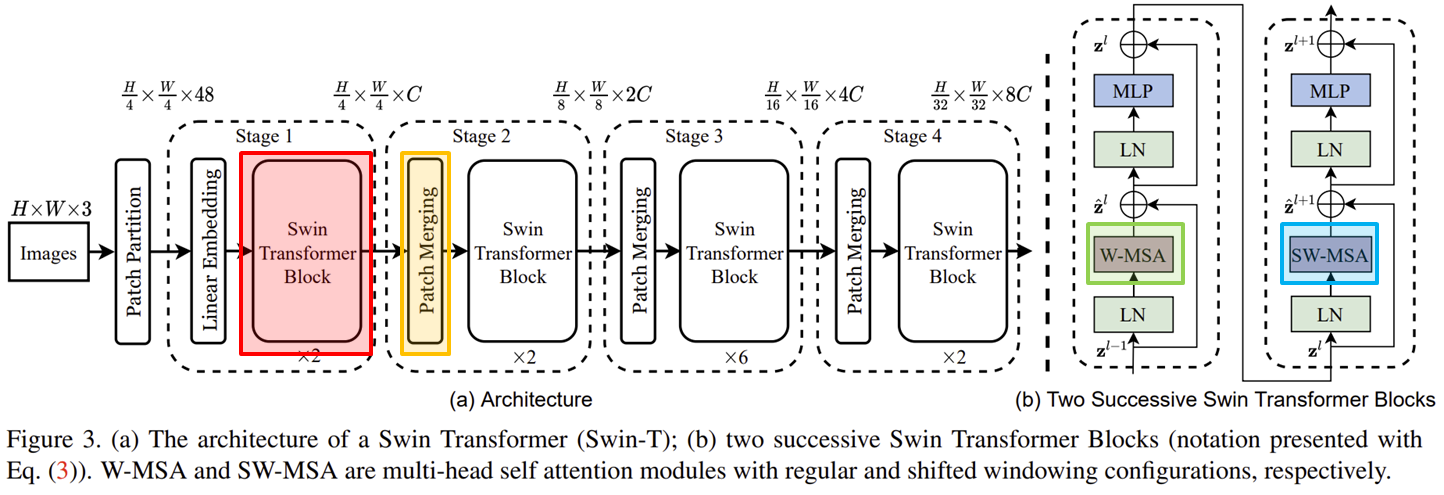
위에서 표시한 대로 핵심을 빨간색 박스의 Swin Transformer Block, Patch Merging, W-MSA, SW-MSA입니다. 해당 구조를 제외하고 나머지는 ViT와 거의 유사합니다.
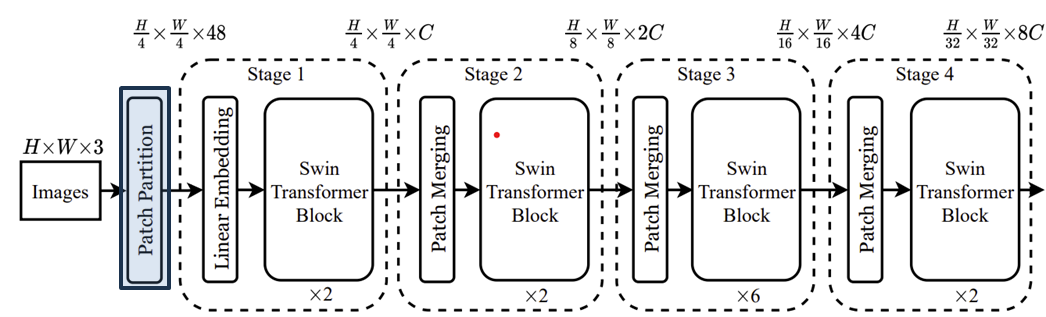
첫번째 단계인 Patch Partition입니다. 이는 ViT와 유사하게 RGB 영상을 겹치지 않는 패치 (non-overlapping patch)로 분해하는 과정입니다. 이때, 각 패치는 토큰 (Token)으로 취급되고 픽셀값들을 하나로 concat하여 사용됩니다. Swin Transformer에서는 패치 크기를 $4 \times 4$로 정의하였습니다. 따라서, 1개의 토큰 차원은 $4 \times 4 \times 3 = 48$이 되겠죠.
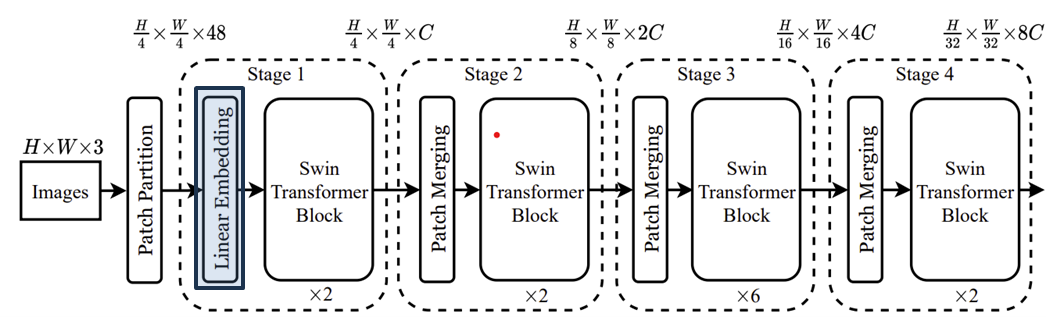
두번째 단계인 Linear Embedding입니다. 이 역시 ViT와 동일하게 각 토큰의 차원을 hidden dimension $C$로 linear projection 시켜주는 과정입니다.
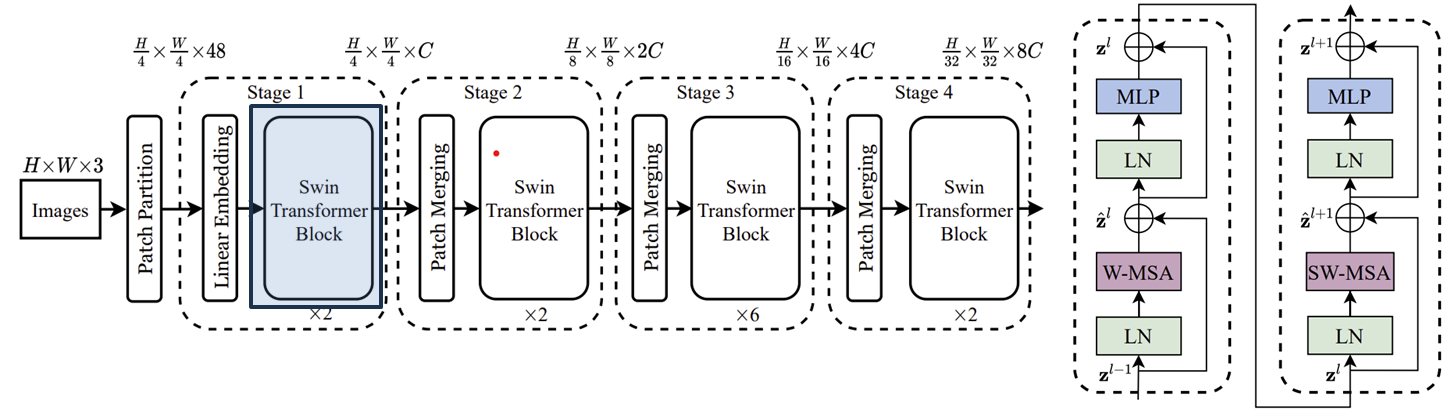
드디어 Swin Transformer Block이 처음으로 나왔습니다. 오른쪽 블록 다이어그램은 Swin Transformer Block을 도식화하고 있습니다. ViT는 MSA를 사용하였지만, Swin Transformer에서는 W-MSA (Window-MSA)와 SW-MSA (Shifted Window MSA)를 사용하고 있네요. 이는 이후에 더 자세히 설명하도록 하겠습니다.
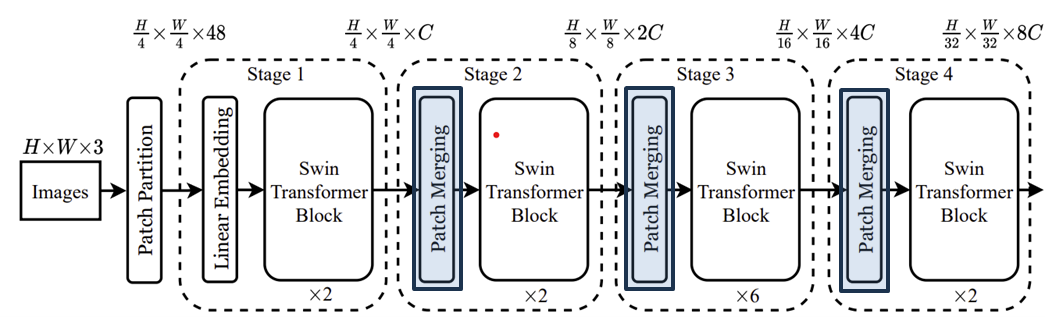
Swin Transformer에서는 Stage 1을 제외하고 나머지 3개의 Stage (Stage 2, 3, 4)에서는 Patch Merging 과정이 포함되어 있습니다. 처음에 Swin Transformer가 등장하게 된 배경에서도 설명드렸다싶이 패치의 크기를 점점 키움으로서 초반 연산량을 줄이는 것을 목표로 하기 때문에 Stage 2, 3, 4의 시작에서 주변 패치를 합쳐주는 과정을 적용하는 것이죠.

처음에 해당 과정이 어떤 식으로 진행되는 지 이해가 잘 되지 않았습니다. 왜냐하면 Linear Embedding을 통해 이미 1D sequence 데이터로 변환된 상태이기 때문이죠. 하지만 그림 1에서는 "실제 패치"가 합쳐지는 듯한 느낌이 들어 이질감이 느껴졌죠. 그래서 저는 위 그림을 기반으로 이해하였습니다. 저희는 현재 16개의 패치를 Linear Embedding을 통해 1D Sequence로 $C$개의 채널의 가지는 데이터 변환되었다고 가정하겠습니다. 그러면 위 그림과 같이 그릴 수 있습니다.
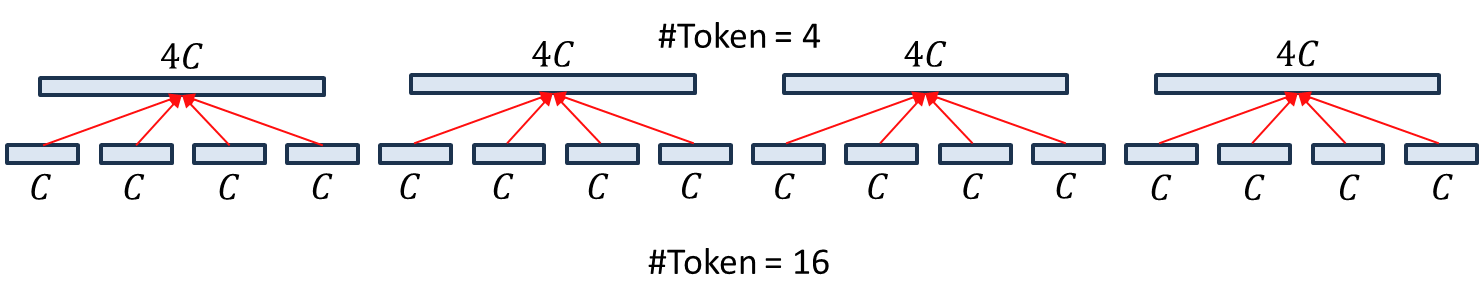
다음으로 논문에서는 $2 \times 2$ 주변의 패치들과 하나로 합친다는 언급을 하고 있습니다. 그러면 위 그림과 같이 4개의 토큰을 하나로 합쳐 $4C$개의 채널을 가지는 새로운 토큰을 만들 수 있습니다. 이를 통해, 원래는 16개의 토큰 (윈도우) 였지만 현재는 4개의 토큰 (윈도우)로 줄어든 것을 볼 수 있습니다.
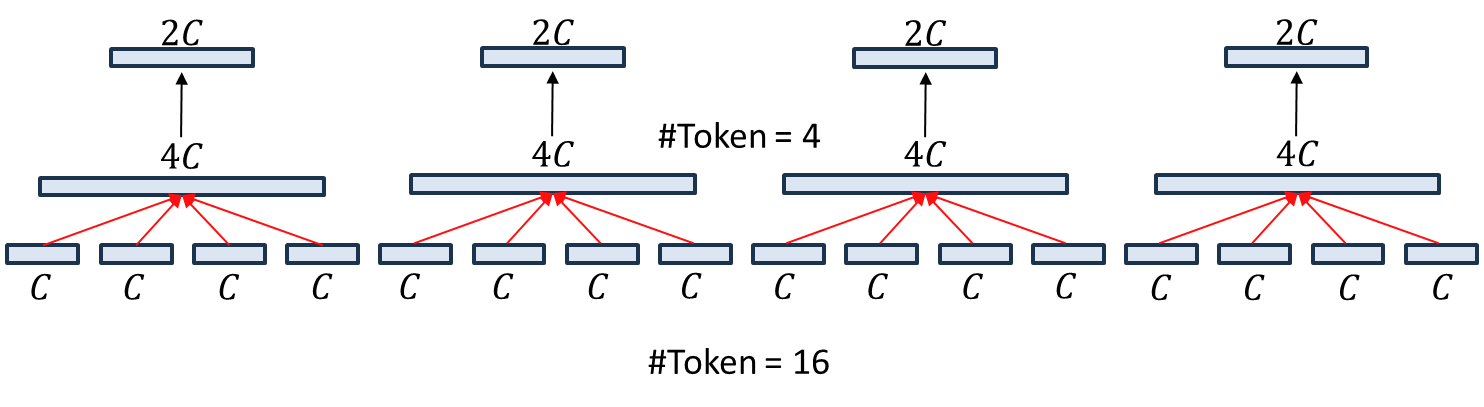
마지막으로 $4C$개의 채널을 가지는 4개의 토큰을 각각 $2C$개의 채널을 가지도록 채널을 감소시켜줍니다. 이때, 토큰의 개수는 영상의 해상도와 동일하기 때문에 한 번의 Patch Merging으로 4배만큼 해상도가 감소하는 것을 볼 수 있죠. 저는 그나마 이렇게 이해하니 어느정도 이해가 갔지만 혹시 틀린 부분이 있다면 말씀해주시면 감사하겠습니다!
2). Shifted Window based Self-Attention
현재 제가 설명을 자세히 안드린 부분이 W-MSA와 SW-MSA입니다. Swin Transformer의 연산량을 줄일 수 있는 핵심 과정은 Patch Merging과 Shifted Window based Self-Attention입니다. 후자가 바로 W-MSA와 SW-MSA이죠.
처음에도 말씀드렸지만 해상도의 제곱만큼 Transformer의 증가하게 됩니다. 현재 저희는 패치의 크기를 $4 \times 4$로 고정하였습니다. 그리고 한 개의 윈도우가 $M \times M$개의 패치를 포함하고 있다고 가정하겠습니다. 이때, 한 개의 영상에서 가로 세로에 각각 $h$개와 $w$개가 있다고 가정하면 영상 크기는 $4Mh \times 4Mw$가 됩니다. 그리고 W-MSA는 하나의 윈도우 내의 패치 간의 self-attention을 계산하기 때문에 다음과 같이 연산량이 감소하게 됩니다.
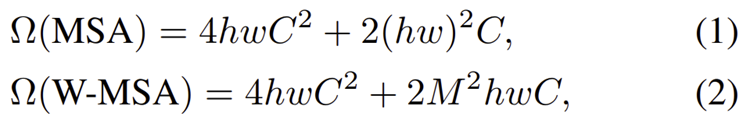
여기서 중요한 것은 ViT의 MSA는 $(hw)^{2}$으로 제곱수만큼 증가하지만 W-MSA에서는 $hw$만큼 증가하는 것을 볼 수 있죠.
하지만, 문제는 또 존재합니다. 저희는 현재 윈도우 내에서만 self-attention을 수행하고 있기 때문에 서로 다른 윈도우 간의 관계성을 이해할 수 없습니다. 이는 기존의 Transformer가 가지고 있던 큰 장점이 없어진 것과 동일합니다. 이러한 문제를 해결하기 위해 본 논문에서는 Shifted Window Partition 방식을 제안합니다.
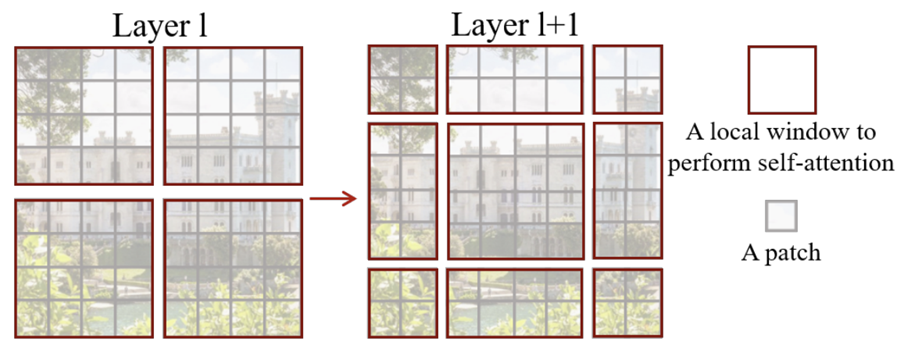
각 Stage의 첫번째 Layer에서는 Layer $l$와 같은 윈도우 configuration을 사용하지만 다음 Layer에서는 서로 다른 윈도우 간 관계성을 추가로 학습하기 위해 새로운 윈도우 configuration을 도입하죠. 그러나 위와 같이 윈도우를 분해하게 되면 각 윈도우에 포함되어 있는 패치의 개수가 다르기 때문에 연산하기 애매해집니다. 패딩을 취할 수는 있지만 이는 공간 복잡도를 늘리기 때문에 본 논문에서는 고려하지 않습니다.
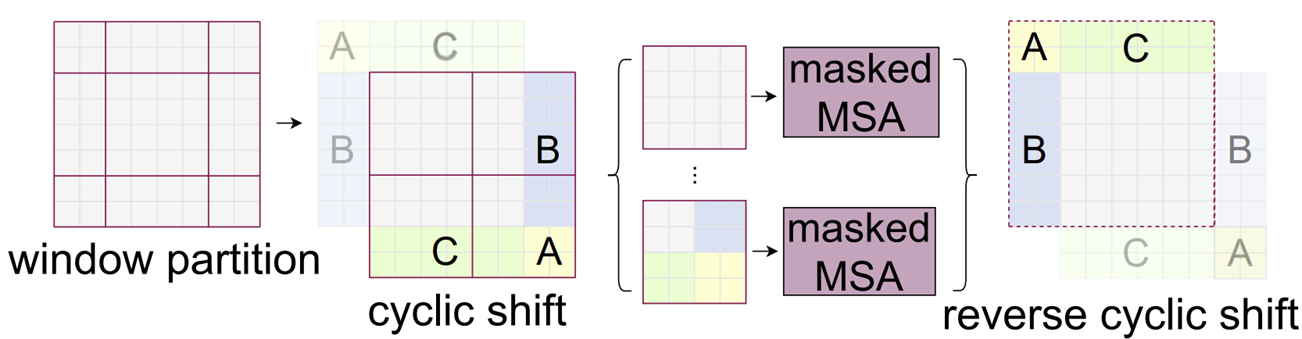
이를 위해 본 논문에서는 위 그림과 같이 Cyclic Shift를 적용합니다. 연한 A (노랑), B (파랑), C (초록)이 보이실 겁니다. 현재 해당 영역이 패치의 개수가 다른 부분이죠. 따라서, 이를 대칭적으로 이동시켜 진한 A (노랑), B (파랑), C (초록)로 옮겨주는 (Shift) 과정을 적용하죠. 그러면 각 윈도우에 대해서 전부 동일한 개수의 패치가 존재하기 때문에 효율적으로 연산을 수행할 수 있습니다. 다만, 진한 A (노랑), B (파랑), C (초록)는 바로 옆에 존재하는 패치들과는 실질적으로 큰 연관이 없기 때문에 masked MSA를 통해 관계성을 줄여줍니다. 연산이끝나게 되면 reverse Cyclic Shift으로 다시 원래 위치로 복귀시켜주게 됩니다.
따라서, Swin Transformer Block 연산을 하나로 정리하면 다음과 같이 쓸 수 있습니다.

3). Architecture Variants

Swin Transformer에서는 모델의 규모에 따라 총 4개의 변형 구조 (Tiny, Small, Base, Large)로 이루어져 있습니다.
Experiment Results
1). Image Classification
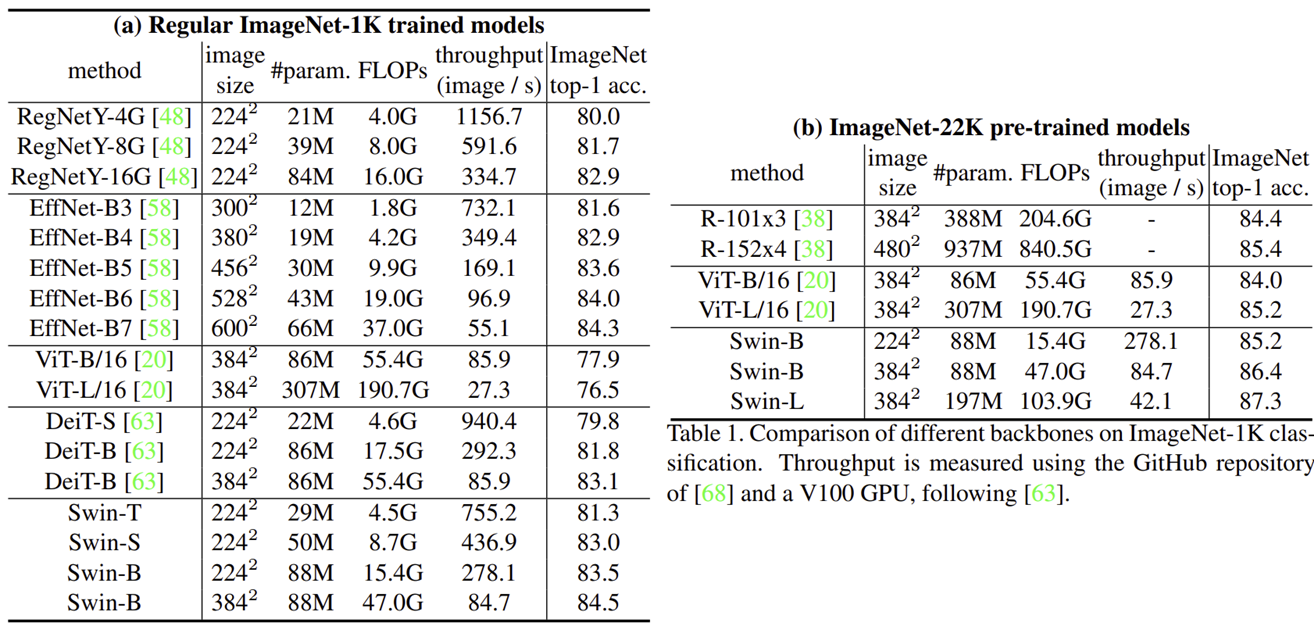
(a)는 ImageNet-1K에 학습한 실험 결과, (b)는 ImageNet-22K에 pre-trained한 결과를 보여주고 있습니다. 보시면 ViT보다도 훨씬 높은 성능을 보여주는 것을 볼 수 있으며 FLOPs도 굉장히 적은 것을 볼 수 있습니다.
2). Object Detection
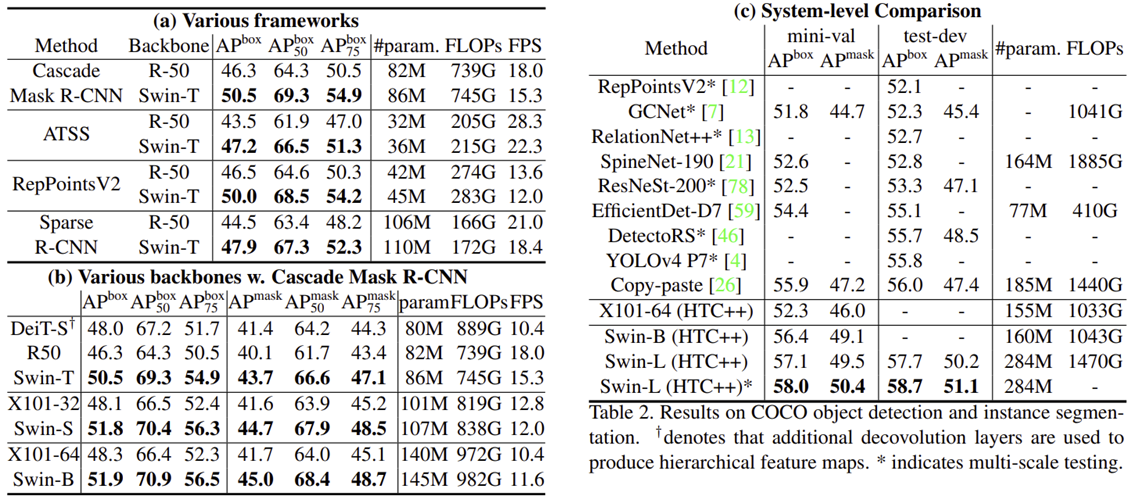
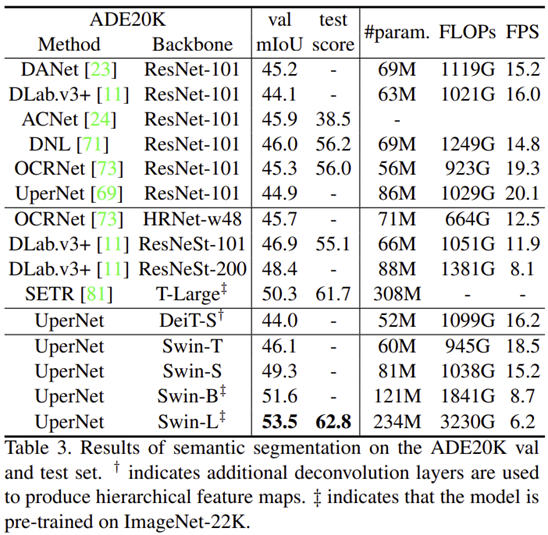
3). Semantic Segmentation