안녕하세요. 지난 포스팅의 [Transformer] Training Data-efficient Image Transformer & Distillation through Attention (ICML2021)에서는 기존의 ViT와 Swin-Transformer에서 수행하는 JFT-300M에 학습 후 ImageNet-1K에 fine-tuning하지 않고 곧바로 ImageNet-1K에 학습해도 성능이 충분히 좋은 모델인 DeiT에 대해서 소개시켜드렸습니다. 오늘은 많은 Transformer 기반 모델에서 핵심 backbone 모델로 자리잡은 Pyramid Vision Transformer (PVT)에 대해서 알아보도록 하겠습니다.
ICCV 2021 Open Access Repository
Pyramid Vision Transformer: A Versatile Backbone for Dense Prediction Without Convolutions Wenhai Wang, Enze Xie, Xiang Li, Deng-Ping Fan, Kaitao Song, Ding Liang, Tong Lu, Ping Luo, Ling Shao; Proceedings of the IEEE/CVF International Conference on Comput
openaccess.thecvf.com
Background
지금까지 컴퓨터 비전과 관련된 많은 연구들은 VGG, InceptionNet, ResNet, EfficientNet과 같은 CNN 기반 모델들에 집중하였습니다. 하지만, 자연어 처리에서 Transformer의 성공은 해당 구조를 컴퓨터 비전에 적용하려는 시도가 많아지게 되었죠. 대표적으로 Vision Transformer (ViT)는 기존의 Transformer 구조를 크게 바꾸지는 않고 이미지를 sequential한 패치단위로 나누어 각각의 패치들에서 global context를 이해할 수 있도록 하였습니다. 이러한 global context는 영상 내에 존재하는 전체적인 정보 혹은 나아가 훈련 데이터셋의 전반적인 특성을 의미합니다. 이는 기존의 CNN 기반 모델에서 가정하는 inductive bias로 인해 얻을 수 없는 정보이기 때문에 Transformer 구조를 컴퓨터 비전에 활용하는 것은 매우 핵심적인 분야가 되었습니다.
하지만, Transformer를 컴퓨터 비전에 이용할 때 발생하는 가장 큰 문제는 복잡성입니다. 일단, Transformer는 내부적으로 모든 패치 간 연관성을 해석하기 위해 self-attention이 적용됩니다. 이는 패치 개수의 제곱만큼의 시간복잡도가 요구됩니다. 그리고 패치의 개수는 입력 영상의 크기가 커질수록 더 늘어나게 됩니다. 따라서, semantic segmentation이나 object detection과 같이 고해상도의 영상을 사용해야하는 분야에서는 활용하기 어렵다라는 문제점이 발생합니다. 이러한 문제를 해결하기 위해 Swin Trasnformer에서는 어텐션 방식을 변경하여 선형에 가까운 시간복잡도를 가지도록 만들었습니다.

하지만 여전히 위 그림과 같이 기존의 Transformer 방식들은 Pyramid 구조를 도입하지 않았기 때문에 multi-scale 정보를 추출할 수 없습니다. 오늘 소개하는 Pyramid Vision Trasnformer (PVT) 역시 이러한 문제점에 주목하여 보다 feature pyramid를 활용하여 효율적인 모델을 만드는 것에 집중합니다. 이를 위해 본 논문에서는 크게 3가지 방식을 도입합니다.
(1). 더 작은 패치 사이즈를 추출
(2). Progressive Shrinking Pyramid
(3). Spatial-Reduction Attention
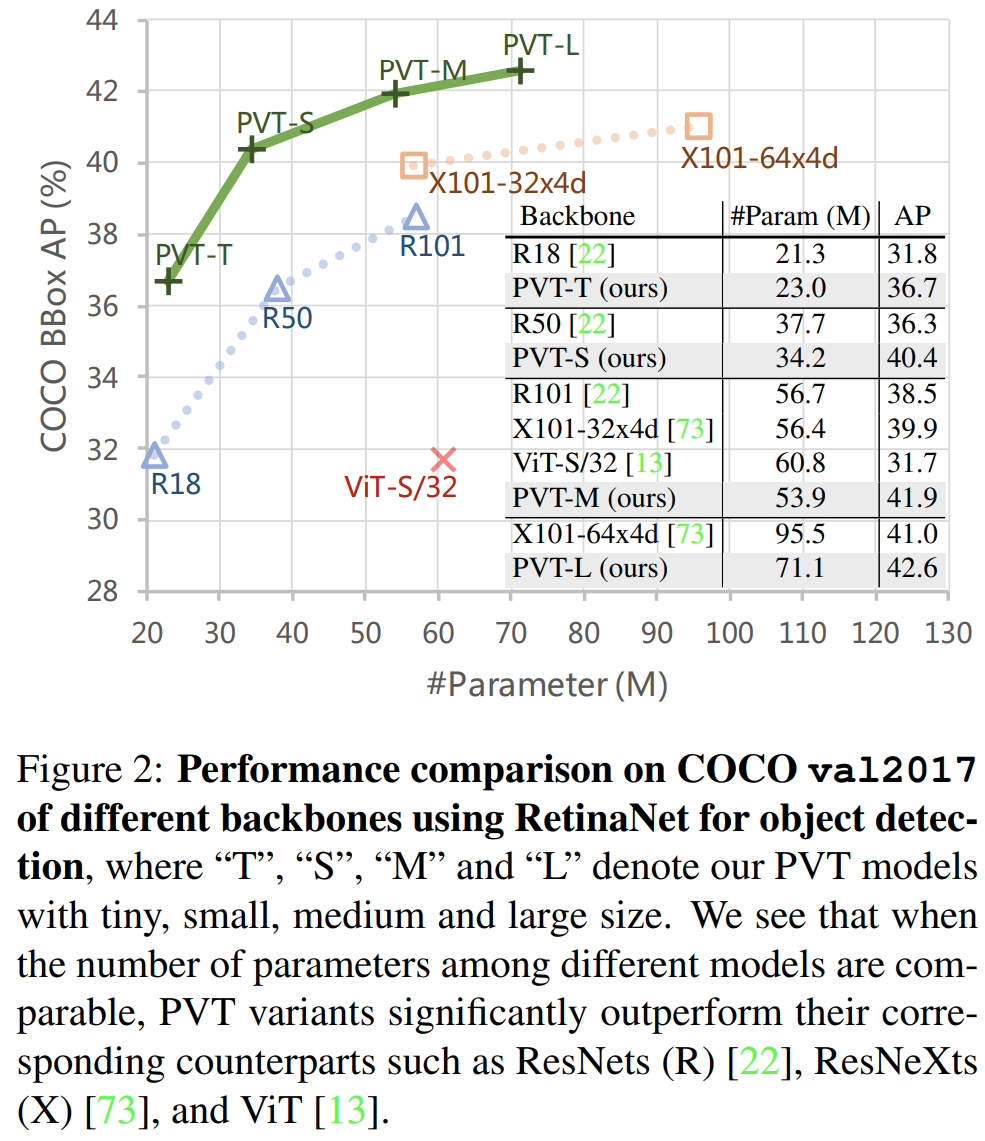
그림2에서 보이다 싶이 이와 같은 방식으로 기존의 Transformer 뿐만 아니라 CNN 기반의 모델들보다도 더 좋은 성능을 달성하였습니다. 또한, 다양한 downstream task에서도 높은 성능을 달성하였죠.
Pyramid Vision Transformer
1). Overall Architecture

그림3은 PVT의 전체적인 구조를 블록 다이어그램으로 시각화하여 보여주고 있습니다. 전체적으로 보았을 때는 ViT와 크게 다르게 보이지는 않지만 핵심은 각 Stage 별로 패치를 추출한다는 점과 SRA이 추가 된 것 입니다. 하지만, 그림 상에서는 pyramid 구조가 보이지 않습니다. 이를 이해하기 위해 좀 더 자세하게 분석해보도록 하죠.
- Patch Extraction: 모든 Stage에서 거의 동일한 방식을 진행하기 때문에 하나의 Stage만 이해해도 충분히 이해할 수 있습니다. Stage1을 기준으로 설명하면 첫번째 단계는 당연히 패치를 추출하는 것입니다. 입력 영상의 크기가 $H \times W \times 3$이라고 가정하면 각 패치의 크기를 $4 \times 4 \times 3$로 추출합니다. 그러면 총 $\frac{HW}{4^{2}}$개의 패치를 얻을 수 있습니다.
- Flatten & Linear Projection: 추출된 각 패치는 현재 3차원 텐서 $4 \times 4 \times 3$이기 때문에 이를 채널 차원을 제외하고 일렬로 쭉 펼쳐줍니다 (Flatten). 그러면 각 패치는 $16 \times 3$ 크기의 벡터로 바뀌게 되겠죠. 다음으로 MLP를 이용하여 linear projection을 시켜줍니다. 그러면 채널이 $C_{1}$으로 늘어나 각 벡터의 형상은 $16 \times C_{1}$이 되겠죠.
- Positional Encoding: 다음으로 각 패치들에 대해 순서 정보를 인코딩하기 위해 position encoding vector를 linear projection된 벡터에 더해줍니다.
- Forward into Encoder: 이제 이전 특징 맵에 대한 모든 전처리 과정을 완료하였으니 Transformer Encoder에 입력해줍니다.
- Reshape: Transformer Encoder를 통과한 특징 맵 $F_{1}$의 크기를 $\frac{H}{4} \times \frac{W}{4} \times C_{1}$으로 재조정합니다.
2). Feature Pyramid for Transformer
위 단계를 거치면 Stage 1을 한번 수행하게 됩니다. 이제 Stage 2, Stage 3, Stage 4에 이전 Stage의 출력 맵을 넣어줄것입니다. 이때, 기존의 ViT에서는 이후 패치 크기를 1로 두었기 때문에 그림1에서 보이는 것과 같이 모든 Stage에서 동일한 크기의 특징 맵들이 만들어집니다. 하지만, PVT에서는 각 Stage별로 서로 다른 크기의 특징 맵을 얻기 위해 패치의 크기를 점점 늘려 출력 특징 맵의 해상도가 점점 줄어들게 됩니다. 이러한 특징 맵들을 모아 $\{ F_{1}, F_{2}, F_{3}, F_{4} \}$로 구성하면 이것이 서로 다른 해상도로 구성된 feature pyramid라고 할 수 있습니다. 본 논문에서는 이와 같이 점진적으로 해상도를 줄이는 방식을 progressive shrinking strategy라고 정의하였습니다.
실제로 $P_{i}$를 $i$번째 Stage의 사용되는 패치의 크기라고 하겠습니다. 그러면 $i$번째 Stage의 첫 단계에서 이전 Stage의 출력 특징 맵인 $F_{i - 1} \in \mathbb{R}^{H_{i - 1} \times W_{i - 1} \times C_{i - 1}}$으로부터 $P_{i} \times P_{i} \times C_{i - 1}$ 크기를 가지는 패치들을 추출해야합니다. 그러면 총 $\frac{H_{i - 1} W_{i - 1}}{P^{2}_{i}}$ 개의 패치들을 얻을 수 있습니다. 그리고 각 패치들을 flatten되어 linear projection을 통해 각 패치의 채널이 $C_{i}$로 바뀝니다. 그러면 입력 특징 맵 $F_{i - 1}$의 해상도보다 $P_{i}$만큼 감소한 $\frac{H_{i - 1}}{P_{i}} \times \frac{W_{i - 1}}{P_{i}} \times C_{i}$를 얻을 수 있게 되는 것이죠.
이 과정을 통해 얻을 수 있는 첫번째 이점은 feature pyramid를 구성함으로써 multi-scale 정보를 활용할 수 있다는 점입니다. 두번째 이점으로는 일반적으로 self-attention을 수행할 때 해상도에 비례한 연산량이 소모되기 때문에 입력 특징 맵보다 $P_{i}$만큼 더 해상도가 감소했기 때문에 보다 효율적인 연산을 수행할 수 있다는 것이겠네요.
3). Spatial-Reduction Attention

마지막 단계는 Spatial-Reduction Attention (SRA)입니다. 그림 4에서 전체적인 과정을 보여주고 있습니다. 기본적인 아이디어는 self-attention 시 해상도에 따라 연산량이 증가하기 때문에 key과 value의 해상도를 어느정도 줄여주고 self-attention을 수행하자는 것입니다.
먼저, key $K$와 value $V$를 크기를 줄여주고 linear projection을 수행하는 $\text{SR} ( \cdot )$을 수행합니다.
$$\text{SR} (\mathbf{x}) = \text{Norm} (\text{Reshape} (\mathbf{x}, R_{i})W^{S})$$
여기서 $\mathbf{x} \in \mathbb{R}^{(H_{i}W_{i}) \times C_{i}}$는 입력 시퀀스로 key 또는 value로 정의됩니다. $R_{i}$는 $i$번째 Stage에서 어텐션 계층의 감소 비율을 의미합니다. 그리고 $\text{Reshape} (\mathbf{x}, R_{i})$는 입력 시퀀스의 형상을 $\mathbb{R}^{(H_{i}W_{i}) \times C_{i}}$를 $\mathbb{R}^{\frac{H_{i}W_{i}}{R^{2}_{i}} \times (R^{2}_{i}C_{i})}$로 바꾸는 것을 의미합니다. 그리고 이때, self-attention을 위해서는 key, value 그리고 query의 채널의 크기는 동일해야하기 때문에 linear projection $W^{S} \in \mathbb{R}^{(R^{2}_{i}C_{i}) \times C_{i}}$를 통해 늘어난 채널의 크기를 다시 $C_{i}$로 줄여줍니다. 그러면 최종적으로 시퀀스의 길이가 감소한 두 key와 value를 얻을 수 있습니다.
다음 단계는 일반적으로 Transformer에서 수행하는 Multi-head Self-Attention (MHSA)를 적용합니다. 이때, 감소된 시퀀스를 이용하여 수행하기 때문에 이를 SRA라고 정의하겠습니다.
$$\text{head}_{j} = \text{Attention} \left( Q W_{j}^{Q}, \text{SR}(K) W_{j}^{K}, \text{SR} (V) W_{j}^{V} \right)$$
$$\text{SRA} (Q, K, V) = \text{Concat} (\text{head}_{0}, \dots, \text{head}_{N_{i}}) W^{O}$$
여기서 $W_{j}^{Q}, W_{j}^{K}, W_{j}^{V} \in \mathbb{R}^{C_{i} \times d_{\text{head}}}$ 그리고 $W^{O} \in \mathbb{R}^{C_{i} \times C_{i}}$인 linear projection들을 의미합니다.
4). Model Variants

ViT와 마찬가지로 각 Stage의 반복 횟수를 기반으로 PVT의 4가지 변형 모델 PVT-Tiny, PVT-Small, PVT-Medium, PVT-Large를 함께 제안합니다. 이때, 연산량은 주로 Stage 3에 집중하여 설계하였습니다.
이와 같은 구조들을 통해 ViT 보다 좋은 점을 크게 3가지 키워드로 정리할 수 있습니다.
- 유연성 (flexibility): 서로 다른 Stage에서 다양한 크기의 스케일과 채널을 만들어낼 수 있기 때문에 ViT에 비해 유연성이 높습니다.
- 다재다능성 (versatility): 다양한 downstream task에 직접적으로 활용할 수 있기 때문에 ViT에 비해 다재다능합니다.
- 효율성 (friendly to memory & computation): self-attention 단계에서 발생하는 연산량 문제를 어느정도 해결하여 기존 ViT에 비해 연산량이 크게 감소하였습니다. 따라서, 고해상도 영상을 사용해야하는 다양한 task에 활용할 수 있습니다.
Application to Downstream Tasks
1). Image-Level Prediction
새로운 모델을 개발할 때 항상 영상 분류에 일차적으로 적용해봐야합니다. PVT 역시 위에서 보이다싶이 4개의 변형 모델인 PVT-Tiny, PVT-Small, PVT-Medium, PVT-Large를 만들었습니다. 그리고 각각의 모델은 ResNet18, ResNet50, ResNet101, ResNet152의 규모에 대응됩니다.
PVT는 ViT와 DeiT와 동일하게 학습 가능한 분류 토큰 (classification token)을 추가하였습니다. 그리고 4번째 Stage 이후 fully-connected layer에 연결하여 영상 분류를 수행합니다.
2). Pixel-Level Dense Prediction
영상 분류만큼이나 중요한 것은 ImageNet-1K에 학습된 모델을 downstream tasks에 적용하는 것입니다. 본 논문에서는 object detection과 semantic segmentation에 적용합니다.
본 논문에서는 3개의 대표적인 dense prediction 모델인 RetinaNet, Mask RCNN, Semantic FPN에 backbone 모델로 적용합니다. 여기서 RetinaNet과 Mask RCNN은 각각 객체 탐지 모델로 single-stage 그리고 two-stage 모델입니다. 그리고 Semantic FPN은 vanilla semantic segmentation 모델입니다.
PVT를 downstream task에 적용하기 위해 다음과 같은 단계를 진행합니다.
STEP1. ResNet과 동일하게 PVT를 ImageNet에 학습한 뒤 해당 가중치로 초기화합니다.
STEP2. PVT의 각 Stage의 출력 맵인 feature pyramid $\{ F_{1}, F_{2}, F_{3}, F_{4} \}$를 FPN의 입력으로 사용합니다. 그리고 object detection과 semantic segmentation head에 각각 입력해줍니다.
STEP3. PVT를 이용해서 학습할 때는 PVT를 포함한 모든 가중치들이 고정되지 않고 업데이트를 수행합니다.
STEP4. object detection과 semantic segmentation를 학습할 때 임의의 크기를 가지는 영상이 입력되기 때문에 ImageNet-1K에서 학습된 positional embedding vector를 직접적으로 더 이상 사용할 수는 없습니다. 따라서, ImageNet-1K의 positional embedding vector를 입력 영상의 크기에 맞춰 bilinear interpolation을 수행하여 맞추어줍니다.
Experiment Results
1). Image Classification
- Dataset: ImageNet-1K
- 1.28 million training images & 50K validation images with 1,000 classes
- 데이터 증강 (DeiT와 동일): random cropping, random horizontal flipping, label-smooting regularization, MixUp, CutMix, Random Erasing
- 최적화 함수: AdamW
- momentum: 0.9
- weight decay: $5 \times 10^{-2}$
- learing rate: 초기 학습률은 $1 \times 10^{-3}$에서 시작하여 cosine annealing learning rate scheduler를 이용하였습니다.
- batch size: 128
- epochs: 300
- 8 V100 GPU
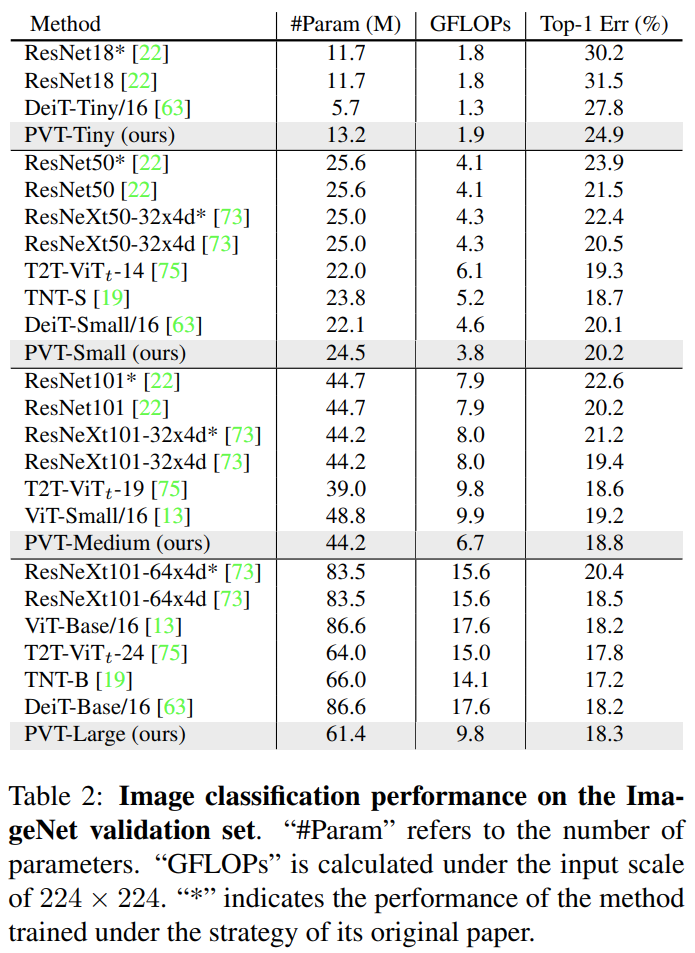
- 표2는 영상 분류에서 실험 결과를 요약하고 있습니다. 성능 자체로만 봤을 때는 PVT-Tiny를 제외하고는 큰 차이는 보이지 않습니다.
- PVT-Tiny에서는 ResNet18과 비교했을 때 파라미터 개수는 2.5M 그리고 0.1GFLOPs 만큼 증가하였지만 성능은 약 7%이 향상되었습니다. 동일한 Transformer 계열 모델인 DeiT에서는 파라미터 및 GFLOPs는 크게 늘어났지만 성능은 3%가 향상되었습니다.
- PVT-Small부터 PVT-Large까지 모두 CNN 계열 모델보다 더 높은 성능을 얻게 되었습니다. 다만, 다른 Transformer 계열보다는 성능이 조금 떨어지는 것을 볼 수 있습니다. 하지만, PVT-Large를 기준으로 비교해보면 파라미터와 GFLOPs는 가장 적지만 T2T-ViT와는 약 0.5%의 성능 차이만 나는 것을 볼 수 있습니다.
2). Object Detection
- Dataset: COCO train2017 (train dataset) & COCO val2017 (evaluation)
- 118k training images & 5k validation images
- Object Detection model: RetinaNet & Mask RCNN
- 최적화 함수: AdamW
- momentum: 0.9
- weight decay: $5 \times 10^{-2}$
- learing rate: $1 \times 10^{-4}$
- batch size: 16
- epochs: -
- 8 V100 GPU
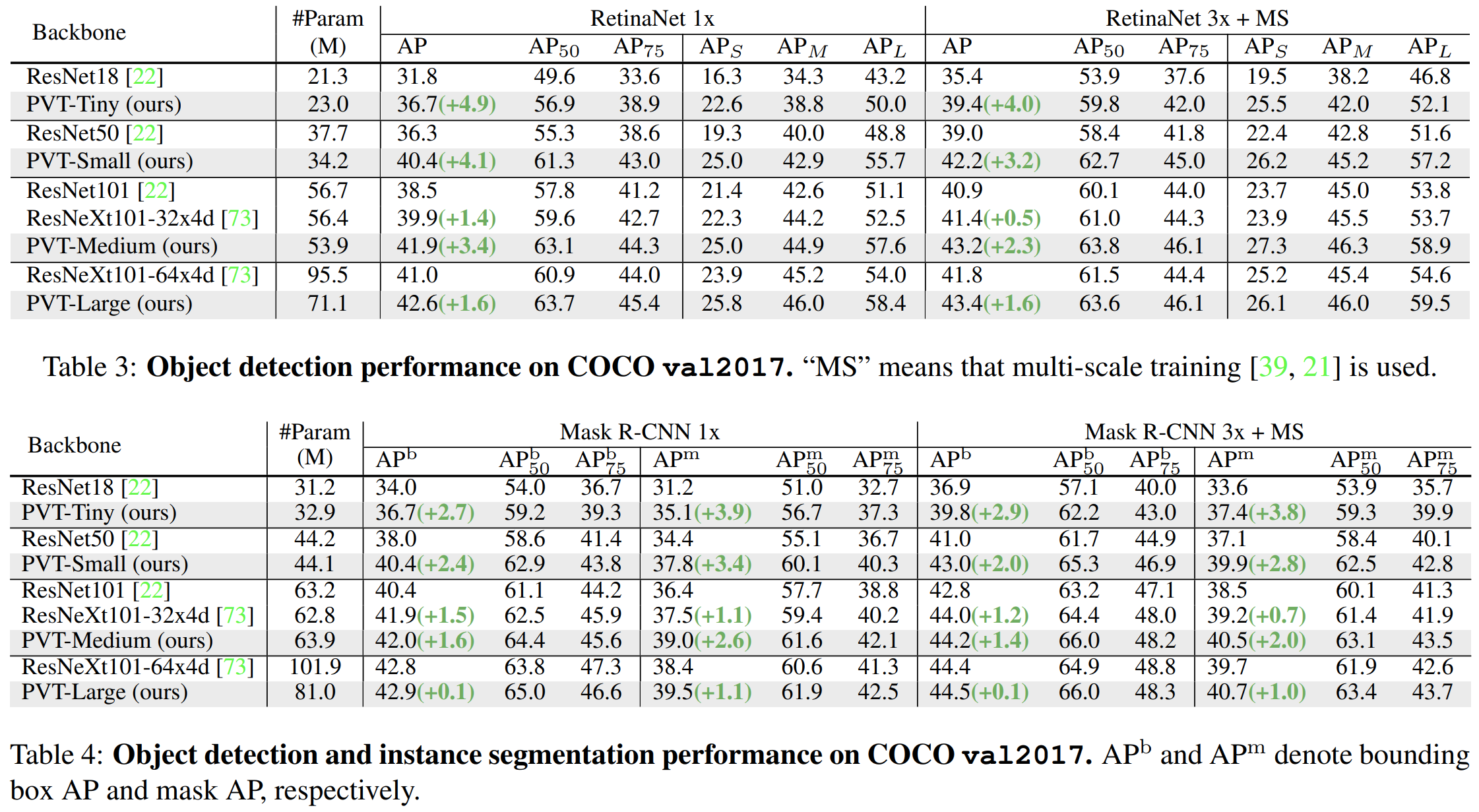
- 표3과 표4는 각각 RetinaNet과 Mask-RCNN을 모델로 했을 때 전체적인 성능을 요약해서 보여주고 있습니다. 결과적으로 CNN 계열을 backbone으로 사용했을 때 보다 더 높은 성능을 달성하였습니다. 뿐만 아니라, 더 중요한 것은 PVT-Tiny를 제외하고는 모두 파라미터의 개수가 CNN 계열 모델보다도 더 낮아지는 것을 볼 수 있습니다.

- 표8에서는 RetinaNet에 ViT를 적용했을 때 결과를 보여주고 있습니다.
- 중요한 것은 PVT에서는 패치의 크기를 4로 해도 충분히 동작하지만 ViT에서 패치의 크기를 4로 하면 Out-of-Memory가 발생하여 동작하지 않습니다. 따라서 ViT에서는 패치의 크기를 32로 진행합니다. 결과적으로 파라미터의 개수는 거의 절반으로 줄었음에도 성능이 10% 가량 향상된 것을 볼 수 있습니다.
3). Semantic Segmentation
- Dataset: ADE20K
- 20,120 training images & 2,000 validation images & 3,352 testing images with 150 fine-grained semantic categories
- Semantic Segmentation model: Semantic FPN
- Randomly Resize & Cropping the image to $512 \times 512$
- 최적화 함수: AdamW
- momentum: 0.9
- weight decay: $5 \times 10^{-2}$
- learing rate: $1 \times 10^{-4}$ with polynomial decay schedule with a power of 0.9
- batch size: 16
- epochs: - (80k iteration)
- 4 V100 GPU

- 표5는 Semantic FPN을 모델로 했을 때 전체적인 성능을 요약해서 보여주고 있습니다. 결과적으로 CNN 계열을 backbone으로 사용했을 때 보다 더 높은 성능을 달성하였습니다. Object Detection과 마찬가지로 PVT-Tiny를 제외하고는 모두 파라미터의 개수가 CNN 계열 모델보다도 더 낮아지는 것을 볼 수 있습니다.
5). Pure Transformer Detection & Segmentation
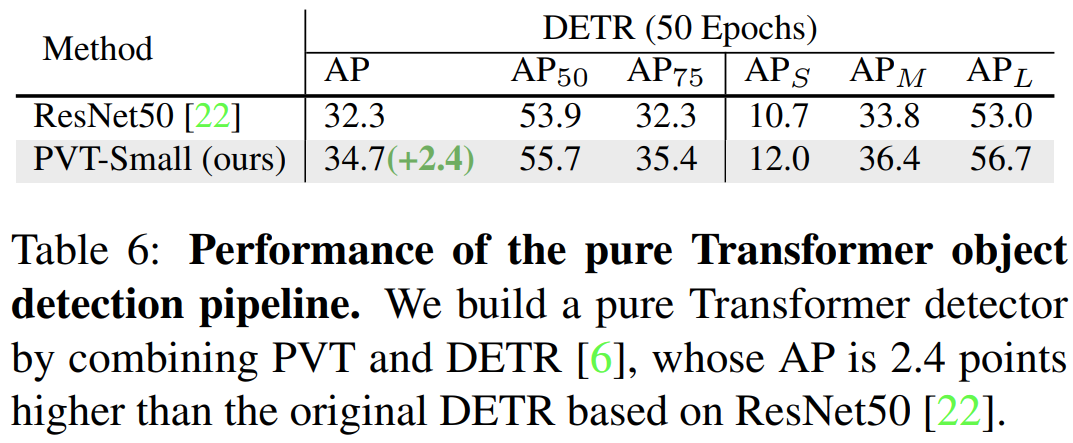

- 지금까지 보았던 downstream task에 적용하는 모델들은 모두 CNN이 존재하였지만 표6과 표7은 완전히 convolution-free 모델인 DETR과 Trans2Seg에 적용하여 각각 Object Detection과 Semantic Segmentation에 대한 성능을 측정하였습니다.
- 결과적으로 모든 부분에서 성능이 향상된 것을 볼 수 있습니다. 뿐만 아니라, Semantic Segmentation에서는 파라미터의 개수와 GFLOPs가 훨씬 낮은 것을 볼 수 있습니다.
Code Analysis
PyTorch 기반의 PVT 전체 코드는 공식 깃허브 사이에서 확인할 수 있습니다.
GitHub - whai362/PVT: Official implementation of PVT series
Official implementation of PVT series. Contribute to whai362/PVT development by creating an account on GitHub.
github.com
핵심적으로 기존 ViT와 비교했을 때 바뀐 전 두 가지만 보도록 하겠습니다.
- Stage 별 입력 영상의 해상도 변화
for i in range(num_stages):
# Input Image Size: 224 (Stage 1) -> 56 (Stage 2) -> 28 (Stage 3) -> 14 (Stage 4)
# Patch size: 4 (Stage 1) -> 2 (Stage 2) -> 2 (Stage 3) -> 2 (Stage 4)
# Input Channels: 3 --(Stage 1)--> 64 --(Stage 2)--> 128 --(Stage 3)--> 256 --(Stage 4)--> 512
# Number of Patches (Input Image Size * Patch size): 3136 = 224 // 4 * 224 // 4 (Stage 1) -> 784 = 56 // 2 * 56 // 2 (Stage 2) -> 196 = 28 // 2 * 28 // 2 (Stage 3) -> 50 = 14 // 2 * 14 // 2 + 1 (Stage 4)
# Positional Embedding Shape: (1, 3136, 64) (Stage 1) -> (1, 784, 128) (Stage 2) -> (1, 196, 256) (Stage 3) -> (1, 50, 512) (Stage 4)
patch_embed = PatchEmbed(img_size=img_size if i == 0 else img_size // (2 ** (i + 1)),
patch_size=patch_size if i == 0 else 2,
in_chans=in_chans if i == 0 else embed_dims[i - 1],
embed_dims=embed_dims[i])
num_patches = patch_embed.num_patches if i != num_stages - 1 else patch_embed.num_patches + 1
"""
Why add 1?
"""
pos_embed = nn.Parameter(torch.zeros(1, num_patches, embed_dims[i]))
pos_drop = nn.Dropout(p=drop_rate)
block = nn.ModuleList([Block(dim=embed_dims[i],
num_heads=num_heads[i],
mlp_ratio=mlp_ratio[i],
qkv_bias=qkv_bias,
qk_scale=qk_scale,
drop_rate=drop_rate,
attn_drop_rate=attn_drop_rate,
drop_path_rate=dpr[cur + j],
norm_layer=norm_layer,
sr_ratio=sr_ratios[i]) for j in range(depths[i])])
cur += depths[i]
setattr(self, f"patch_embed{i + 1}", patch_embed)
setattr(self, f"pos_embed{i + 1}", pos_embed)
setattr(self, f"pos_drop{i + 1}", pos_drop)
setattr(self, f"block{i + 1}", block)
각 스테이지를 정의할 때 볼 수 있는 코드 라인입니다. 각 스테이지의 입력 크기가 224 $\rightarrow$ 56 $\rightarrow$ 28 $\rightarrow$ 14와 같이 줄어드는 것을 볼 수 있습니다. 이와 같이 여러 개의 해상도를 가지는 feature pyramid 구조를 활용한다는 점이 PVT의 가장 큰 특징이라고 볼 수 있습니다.
이 과정에서 패치의 크기는 처음에 4로 정한 뒤 이후 스테이지에서는 2로 바꾸어줍니다. 즉, 더 작은 패치를 기반으로 더욱 세세한 global context를 확인하겠다는 의미겠죠. 이렇게 되면 각 스테이지에서 얻는 패치의 개수는 3136 $\rightarrow$ 784 $\rightarrow$ 196 $\rightarrow$ 50개가 됩니다. 그런데 마지막 스테이지에서 패치의 개수를 한 개 더해주는 데 이유는 모르겠습니다. 혹시 아시는 분은 댓글로 남겨주시면 감사하겠습니다.
- Spatial-Reduction Attention
class Attention(nn.Module):
"""
Self-Attention Module
Args:
dim: input feature dimension
num_heads: number of heads
qkv_bias: qkv bias
qk_scale: qk scale
attn_drop_rate: attention dropout rate
proj_drop_rate: projection dropout rate
sr_ratio: sr ratio
"""
def __init__(self,
dim: int,
num_heads: int=8,
qkv_bias: bool=False,
qk_scale: Optional[float]=None,
attn_drop_rate: float=0.,
proj_drop_rate: float=0.,
sr_ratio: Optional[int]=1):
super(Attention, self).__init__()
self.dim = dim
self.num_heads = num_heads
head_dim = dim // num_heads
self.scale = qk_scale or head_dim ** -0.5
self.q = nn.Linear(dim, dim, bias=qkv_bias)
self.kv = nn.Linear(dim, dim * 2, bias=qkv_bias)
self.attn_drop = nn.Dropout(attn_drop_rate)
self.proj = nn.Linear(dim, dim)
self.proj_drop = nn.Dropout(proj_drop_rate)
self.sr_ratio = sr_ratio
if sr_ratio > 1:
self.sr = nn.Conv2d(dim, dim, kernel_size=sr_ratio, stride=sr_ratio)
self.norm = nn.LayerNorm(dim)
def forward(self, x, H, W):
B, N, C = x.shape
q = self.q(x).reshape(B, N, self.num_heads, C // self.num_heads).permute(0, 2, 1, 3)
if self.sr_ratio > 1:
x_ = x.permute(0, 2, 1).reshape(B, C, H, W)
x_ = self.sr(x_).reshape(B, C, -1).permute(0, 2, 1)
x_ = self.norm(x_)
kv = self.kv(x_).reshape(B, -1, 2, self.num_heads, C // self.num_heads).permute(2, 0, 3, 1, 4)
else:
kv = self.kv(x).reshape(B, -1, 2, self.num_heads, C // self.num_heads).permute(2, 0, 3, 1, 4)
k, v = kv[0], kv[1]
attn = (q @ k.transpose(-2, -1)) * self.scale
attn = attn.softmax(dim=-1)
attn = self.attn_drop(attn)
x = (attn @ v).transpose(1, 2).reshape(B, N, C)
x = self.proj(x)
x = self.proj_drop(x)
return x
이 부분은 Attention Block에서 확인해볼 수 있습니다. sr_ratio를 1보다 크게 지정함으로써 해당 모듈을 동작시킬 수 있습니다. 다시 한번 SRA의 핵심을 상기하면 Key와 Value의 크기를 줄임으로써 self-attention에서 발생하는 연산량을 줄이는 것 입니다. 이는 간단하게 합성곱 연산을 통해 해결할 수 있습니다.
- Model Variants
@register_model
def pvt_tiny(pretrained=False, **kwargs):
model = PyramidVisionTransformer(patch_size=4,
embed_dims=[64, 128, 320, 512],
num_heads=[1, 2, 5, 8],
mlp_ratio=[8, 8, 4, 4],
qkv_bias=True,
norm_layer=partial(nn.LayerNorm, eps=1e-6),
depths=[2, 2, 2, 2],
sr_ratios=[8, 4, 2, 1],
**kwargs)
model.default_cfg = _cfg()
return model
@register_model
def pvt_small(pretrained=False, **kwargs):
model = PyramidVisionTransformer(patch_size=4,
embed_dims=[64, 128, 320, 512],
num_heads=[1, 2, 5, 8],
mlp_ratio=[8, 8, 4, 4],
qkv_bias=True,
norm_layer=partial(nn.LayerNorm, eps=1e-6),
depths=[3, 4, 6, 3],
sr_ratios=[8, 4, 2, 1],
**kwargs)
model.default_cfg = _cfg()
return model
@register_model
def pvt_medium(pretrained=False, **kwargs):
model = PyramidVisionTransformer(patch_size=4,
embed_dims=[64, 128, 320, 512],
num_heads=[1, 2, 5, 8],
mlp_ratio=[8, 8, 4, 4],
qkv_bias=True,
norm_layer=partial(nn.LayerNorm, eps=1e-6),
depths=[3, 4, 18, 3],
sr_ratios=[8, 4, 2, 1],
**kwargs)
model.default_cfg = _cfg()
return model
@register_model
def pvt_large(pretrained=False, **kwargs):
model = PyramidVisionTransformer(patch_size=4,
embed_dims=[64, 128, 320, 512],
num_heads=[1, 2, 5, 8],
mlp_ratio=[8, 8, 4, 4],
qkv_bias=True,
norm_layer=partial(nn.LayerNorm, eps=1e-6),
depths=[3, 8, 27, 3],
sr_ratios=[8, 4, 2, 1],
**kwargs)
model.default_cfg = _cfg()
return model
공식코드에서는 pvt_huge를 포함하여 5개의 변형 모델을 제시하지만 논문에 맞춰서 저희는 4가지만 보도록 하겠습니다. 각 변형 모델에서 다른 점은 depth로 3번째 Stage에 주로 연산량을 크게 주는 것을 볼 수 있습니다.
