안녕하세요. 지난 포스팅의 [IC2D] Big-Little Net: An Efficient Multi-Scale Feature Representation for Visual and Speech Recognition (ICLR2019)에서는 높은 연산량을 필요로 하는 high-scale 영상은 low-branch, 적은 연산량을 필요로 하는 low-scale은 추가적인 정보를 추출하기 위해 high-branch에 입력하여 연산량을 감소시키는 bL-Net에 대해서 알아보았습니다. 오늘은 지금까지 알아본 Attention 기반 모델과는 살짝 방향성이 다른 Self-Calibrated Convolution에 대해서 알아보도록 하겠습니다.
CVPR 2020 Open Access Repository
Jiang-Jiang Liu, Qibin Hou, Ming-Ming Cheng, Changhu Wang, Jiashi Feng; Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2020, pp. 10096-10105 Recent advances on CNNs are mostly devoted to designing more complex arc
openaccess.thecvf.com
Background
지금까지 제안된 많은 CNN 모델들은 ImageNet-1K와 같은 대규모 데이터셋을 기반으로 강력한 표현력을 가지는 모델을 얻을 수 있게 되었습니다. 이를 통해, 객체 탐지 (Object Detection), 의미론적 분할 (Semantic Segmentation)과 같은 down-stream tasks에 활용할 수 있게 되었죠. 이러한 경향성은 성능 좋은 영상 분류 모델은 down-stream task에서도 강력한 표현력을 위해 활용될 수 있다는 것을 입증합니다. 따라서, CNN을 활용한 영상 분류 연구의 목적은 단순히 영상 분류만이 아닌 CNN의 특징 변환 능력을 향상시킴으로써 다양한 어플리케이션에서 활용할 수 있게 하는 것입니다.
이를 위해, 지금까지 저희는 많은 논문들을 보았습니다. 대표적으로 ResNet 기반 모델들 (ResNet, PreAct ResNet, WRN, ResNet-Inception, PyramidNet, ResNeXt, Res2Net, ...)등이 있었죠. 또한, AutoML 기반의 NASNet과 PNASNet도 보았습니다. 뿐만 아니라, Attention 기반은 방법들인 RAN, SENet, BAM, CBAM, SKNet과 같은 모델들도 보았습니다. 이러한 방법들의 공통적인 아이디어는 풍부한 특징을 추출할 수 있는 CNN의 표현력을 강화시키는 것입니다.
오늘 알아볼 Self-Calibrated Convolution은 Attention 기반 모델과 어느정도 유사하다고 볼 수 있습니다. 그러나 기존의 Attention 기반 모델들이 Fully-Connected Layer를 활용하여 Channel Recalibration을 위한 attention map을 추출하는 방식을 사용하기 때문에 어느정도 파라미터 및 연산량이 더해질 수 밖에 없습니다. Self-Calibrated Convolution은 추가적인 파라미터를 전혀 사용하지 않고도 성능 향상을 달성한 방법으로 Attention 모델에서 굉장히 효율적인 방식이라고 볼 수 있습니다.
Method
1). Overall Architectures

그림2는 Self-Calibrated (SC) Convolution의 전체적인 블록 다이어그램을 보여주고 있습니다. 기본적으로 본 논문에서 잡은 컨셉은 "파라미터 증가없이 Attention을 수행할 수 없을까?"입니다. 따라서, SC Convolution에서는 이미 정의된 개수의 필터의 개수를 group 단위로 나누어 연산을 수행하게 되죠. 이를 좀 더 자세히 보도록 하겠습니다.
일단, $\mathcal{F}(\cdot)$가 $\mathbf{K} = [\mathbf{k}_{1}, \dots, \mathbf{k}_{\hat{C}}]$를 필터로 가지는 2D 합성곱 연산이라고 가정하겠습니다. 이때, $\mathbf{k}_{i}$는 $i$번째 필터로 총 $C$개의 채널을 출력값으로 보낸다고 가정하겠습니다. 그러면 입력 특징맵 $\mathbf{X} = [\mathbf{x}_{1}, \dots, \mathbf{x}_{C}] \in \mathbb{R}^{C \times H \times W}$에 대해서 다음과 같이 출력 특징맵 $\mathbf{Y} = [\mathbf{y}_{1}, \dots, \mathbf{y}_{\hat{C}}] \in \mathbb{R}^{\hat{C} \times \hat{H} \times \hat{W}}$를 얻을 수 있습니다.
$$\mathbf{Y} = \mathbf{k}_{i} * \mathbf{X} = \sum_{j = 1}^{i} \mathbf{k}_{i}^{j} * \mathbf{x}_{j}$$
2D 합성곱 연산의 특징은 커널 크기에 비례하여 수용 영역 (Receptive Field)가 늘어난다는 점입니다. 수용 영역은 하나의 출력 픽셀을 결정할 때 입력 특징 맵에서 얼마나 넓은 영역을 보고 얻는 지에 대한 것으로 넓을 수록 영상의 전체적인 문맥을 판단할 수 있기 때문에 중요한 요소입니다. 만약, 작은 커널로 이루어져있다면 수용 영역이 좁아 long-range dependency를 얻지 못해 영상의 문맥 파악이 어려워지게 됩니다.
2). Self-Calibrated Convolution
이러한 문제를 해결하기 위해 제안된 SC Convolution을 설명하도록 하겠습니다. 먼저 편의를 위해 $\hat{C} = C$, 즉 출력 특징 맵과 입력 특징 맵의 채널의 개수가 동일하다고 가정하겠습니다. 그리고, $\mathbf{K} = [\mathbf{k}_{1}, \dots, \mathbf{k}_{C}] \in \mathbb{R}^{C \times C \times k_{h} \times k_{w}}$이 필터 그룹으로 주어졌다고 가정합니다. 본 논문에서는 문제 필터 그룹 $\mathbf{K}$를 4개의 서브-그룹 필터로 나누어줍니다.
$$\mathbf{K} = \{ \mathbf{K}_{i} \}_{i}^{C}$$
여기서, $C$가 2로 나누어 떨어진다고 가정하겠습니다.

다음으로 입력 특징 맵 $\mathbf{X}$를 두 개의 특징맵으로 나누어 서로 다른 path에 입력해줍니다. $\mathbf{X} = \{ \mathbf{X}_{1}, \mathbf{X}_{2} \}$라고 하면 $\mathbf{X}_{1}$은 Self-Calibration path 그리고 $\mathbf{X}_{2}$은 Original path로 넘겨줍니다. 이때, 각 path로 넘겨지는 특징 맵의 채널의 개수는 $\frac{C}{2}$가 됩니다.

Self-Calibration path도 여러 개의 서브 path로 구성되어 있습니다. 첫번째로 설명하는 것은 $r \times$ Down이라고 적힌 파트입니다. 이 부분은 Self-Calibration을 수행할 때 multi-scale 정보도 함께 고려하기 위해 $\mathbf{X}_{1}$을 $r$배 만큼 해상도를 줄여주게 됩니다. 다음으로 처음에 저희가 나누었던 4개의 서브 필터 중 $\mathbf{K}_{2}$를 이용해 변환하게 되죠. 이 과정을 작성하면 다음과 같습니다.
$$\begin{cases} \mathbf{T}_{1} &= \text{AvgPool}_{r} (\mathbf{X}_{1}) \\ \mathbf{X}_{1}^{'} &= \text{Up} (\mathcal{F}_{2} (\mathbf{T}_{1})) \end{cases}$$

이제 Self-Calibration의 두번째 path에 $\mathbf{X}_{1}$을 넘겨주어 위의 calibration map을 통해 다음과 같이 attention을 수행합니다.
$$\mathbf{Y}^{'}_{1} = \mathcal{F}_{3} (\mathbf{X}_{1}) \cdot \sigma (\mathbf{X}_{1} + \mathbf{X}_{1}^{'})$$

Self-Calibration path의 마지막 단계로 $\mathbf{K}_{4}$를 이용해 한번 더 특징 맵을 변환해줍니다.
$$\mathbf{Y}_{1} = \mathcal{F}_{4} (\mathbf{Y}^{'}_{1})$$
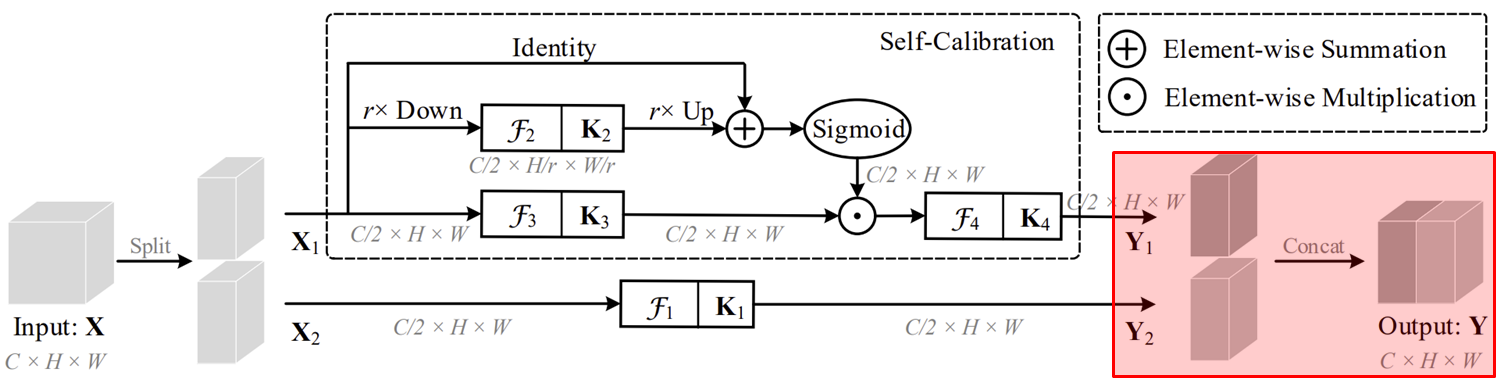
마지막으로 original path와 self-calibration path의 출력 특징 맵을 하나로 concatenation하여 다음 계층으로 보내줍니다. 위와 같이 진행했을 때 처음에 본 논문에서 목표로 하던 것과 같이 추가적이 파라미터를 사용하지 않고도 Attention이 달성될 수 있다는 것에 큰 의의가 있습니다.
Experiment Results

표1은 ResNet 계열의 모델에 SC Convolution을 추가했을 때 ImageNet-1K에서의 성능을 보여주고 있습니다. 파라미터는 SC Convolution을 적용하기 전 후 동일한 것을 볼 수 있죠. 심지어 연산량은 오히려 감소한 것을 볼 수 있습니다. 이는 필터의 개수는 동일하지만 중간에 채널 크기의 감소 + 해상도의 감소로 인한 것으로 볼 수 있습니다. 또한, 분류 성능 역시 모든 부분에서 크게 향상된 것을 볼 수 있습니다.
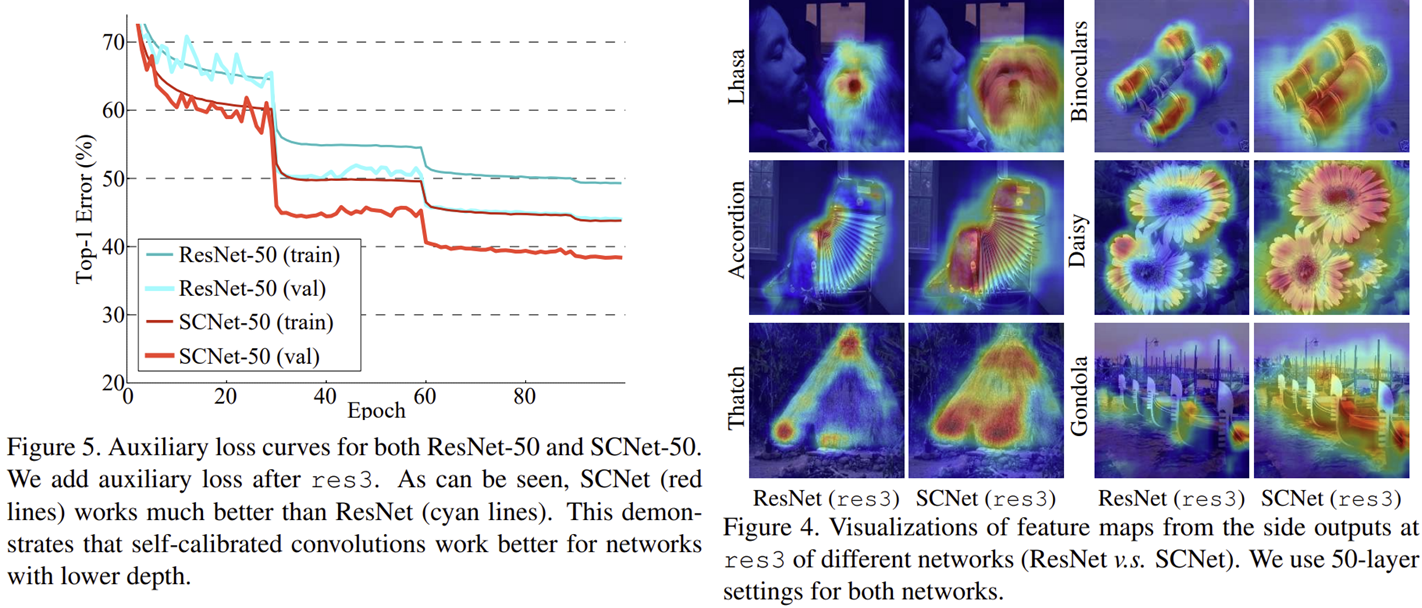
다음으로 그림5와 그림4는 SC Convolution과 Vanilla Convolution 사이의 손실함수 그래프와 Grad-CAM 결과를 보여주고 있습니다. 결과적으로 과적합이 방지가 되었으며 특징을 잡아내는 능력도 크게 향상되는 것을 볼 수 있습니다.
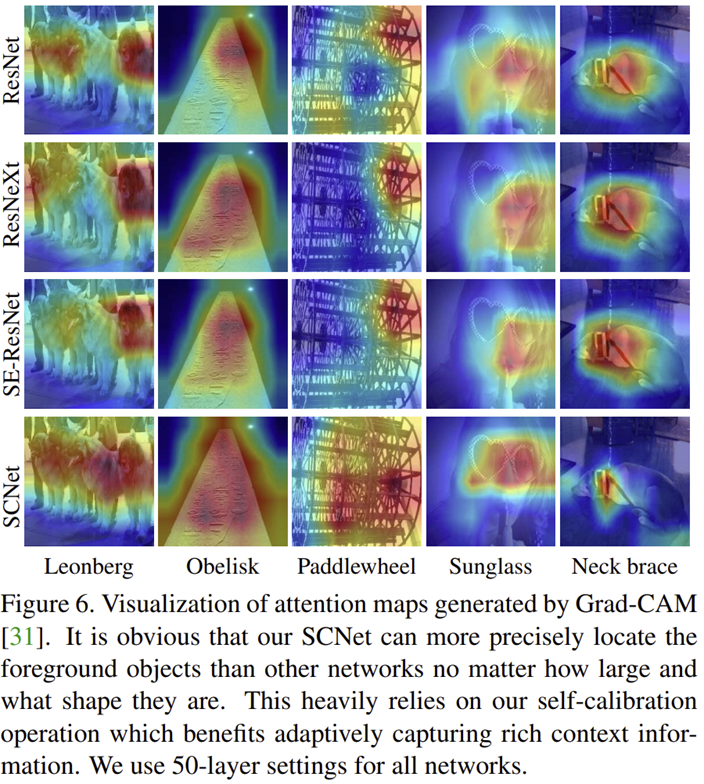
그림6은 Attention 기반의 모델과도 비교했을 때도 마찬가지임을 볼 수 있습니다.
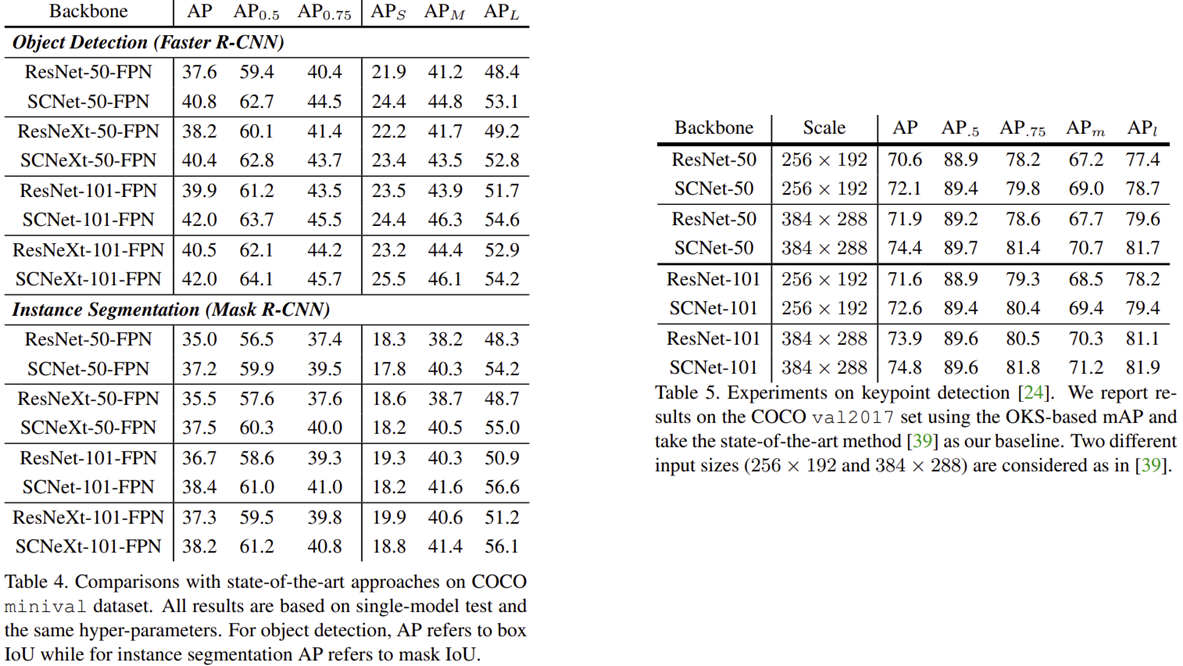
표4와 표5는 객체 탐지, 인스턴스 분할, 사람 키포인트 탐지와 같은 어플리케이션에서 SC Convolution을 적용했을 때 성능 향상 정도를 보여주고 있습니다.
