안녕하세요. 지난 포스팅의 미적분학 - 특이적분에서는 무한대가 포함된 구간의 적분과 불연속점에 포함된 피적분함수의 적분에 대해서 알아보았습니다. 핵심은 임의의 실수 $t$를 선택한 뒤 무한 또는 불연속점으로 극한을 취해주면 되었습니다. 이때, 항상 극한이 존재하는 것이 아니기 때문에 특이적분에서는 값이 존재하지 않을 수도 있습니다. 오늘은 적분의 새로운 응용으로 호의 길이를 구하는 방법에 대해서 알아보도록 하겠습니다.
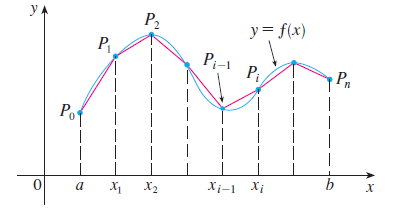
위 그림과 같이 함수 $y = f(x)$가 있다고 가정하겠습니다. 저희가 원하는 것은 구간 $[a, b]$까지의 함수 $f(x)$의 자취인 곡선 $C$의 길이 $L$를 구하는 것입니다. 일단, 길이를 어떻게 구할 수 있는 지부터 생각해보겠습니다. 길이라는 것은 시작점과 끝점이 주어지며 두 점 사이의 거리를 의미합니다. 따라서, 곡선의 길이를 구하기 위해서는 시작점과 끝점을 정해야겠죠. 이를 $P_{0}$와 $P_{n}$이라고 하겠습니다. 만약, $n = 1$이라고 한다면, 구간 $[a, b]$를 그대로 쓰는 것으로 $x_{0}$와 $x_{1}$만 존재하는 것을 의미합니다. 좀 더 정확한 곡선의 길이를 구하기 위해서는 $n$을 늘리면 되겠죠? 따라서, 구간을 등구간 $[x_{i - 1}, x_{i}]$으로 나누면 각 구간의 길이는 $\Delta x$가 됩니다. 그리고 이에 대응되는 곡선위의 점을 편의상 $P_{i}(x_{i}, y_{i}) = P_{i}$이라고 쓰겠습니다.
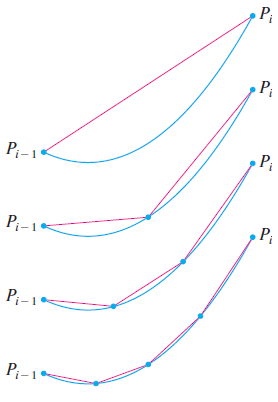
위 그림을 보시면 곡선 $C$의 길이는 다각형의 길이의 합으로 생각해볼 수 있습니다. 즉, $\sum_{i = 1}^{n} \left|P_{i - 1}P_{i}\right|$이죠. 이때, $\left|P_{i -1}P_{i}\right|$란 두 점 $P_{i - 1}$과 $P_{i}$ 사이의 길이를 의미합니다. 그리고 정확한 곡선의 길이 $L$은 $n$에 극한을 취해서 얻을 수 있습니다.
$$L = \lim_{n \rightarrow \infty} \sum_{i = 1}^{n} \left|P_{i - 1}P_{i}\right|$$
이제 저희가 할 일은 $\left|P_{i - 1}P_{i}\right|$를 구하는 것입니다. 기본적으로 직교좌표 상에서 두 점 사이의 거리는 아래와 같습니다.
$$\left|P_{i - 1}P_{i}\right| = \sqrt{(x_{i} - x_{i - 1})^{2} + (y_{i} - y_{i - 1})^{2}} = \sqrt{(\Delta x)^{2} + (\Delta y)^{2}}$$
이때, 중요한 점은 여기서 평균값 정리(Mean Value Theorem, MVT)를 활용해야합니다. 평균값 정리의 자세한 설명은 아래의 링크를 참조해주시길 바랍니다.
미적분학 - 평균값 정리
안녕하세요. 지난 포스팅의 미적분학 - 최대값과 최소값에서는 전역최대 및 전역최소의 정의, 그리고 지역최대 및 지역최소의 정의, 마지막으로 임계값에 대해서 알아보았습니다. 그리고 이와
everyday-image-processing.tistory.com
$$\begin{align*} \Delta y &= y_{i} - y_{i - 1} \\ &= f(x_{i}) - f(x_{i - 1}) \\ &= f^{*}(x_{i}^{'})(x_{i} - x_{i - 1}) \\ &= f^{'}(x_{i}^{*}) \Delta x\end{align*}$$
따라서, 저희는 기존의 식을 아래와 같이 바꿀 수 있습니다.
$$\begin{align*} \left|P_{i - 1}P_{i}\right| &= \sqrt{(x_{i} - x_{i - 1})^{2} + (y_{i} - y_{i - 1})^{2}} \\ &= \sqrt{(\Delta x)^{2} + (\Delta y)^{2}} \\ &= \sqrt{(\Delta x)^{2} + (f^{'}(x_{i}^{*}) \Delta x)^{2}} \\ &= \sqrt{1 + \left[f^{'}(x_{i}^{*})\right]^{2}} \Delta x\end{align*}$$
그러므로 저희가 원하는 곡선의 길이 $L$은 아래와 같습니다.
$$\begin{align*} L &= \lim_{n \rightarrow \infty} \sum_{i = 1}^{n} \left|P_{i - 1}P_{i}\right| \\ &= \lim_{n \rightarrow \infty} \sum_{i = 1}^{n} \sqrt{1 + \left[f^{'}(x_{i}^{*})\right]}\Delta x \\ &= \int_{a}^{b} \sqrt{1 + \left[f^{'}(x)\right]^{2}} \; dx\end{align*}$$
예제1. 두 점 $(1, 1)$과 $(4, 8)$사이의 포물선 $y^{2} = x^{3}$의 길이를 구하여라.
$y^{2} = x^{3} \Rightarrow y = x^{\frac{3}{2}}$이기 때문에 미분하면 $\frac{dy}{dx} = \frac{3}{2}x^{\frac{1}{2}}$이다. 이제, 곡선의 길이를 구하기 위해 공식을 적용한다.
$$\begin{align*} L &= \int_{1}^{4} \sqrt{1 + \frac{9}{4}x} \; dx \end{align*}$$
여기서 $1 + \frac{9}{4}x = u$라고 하면 $x = 1 \rightarrow u = \frac{13}{4}, x = 4 \rightarrow u = 10$이고 $\frac{9}{4}dx = du \Rightarrow dx = \frac{4}{9}du$이기 때문에 아래와 같이 치환적분이 가능하다.
$$\begin{align*} L &= \int_{1}^{4} \sqrt{1 + \frac{9}{4}x} \; dx \\ &= \int_{\frac{13}{4}}^{10} \sqrt{u} \; \left(\frac{4}{9}du\right) \\ &= \frac{4}{9} \int_{\frac{13}{4}}^{10} \sqrt{u} \; du \\ &= \frac{4}{9} \left[\frac{2}{3} u^{\frac{3}{2}}\right]_{\frac{13}{4}}^{10} \\ &= \frac{8}{27} \left[10^{\frac{3}{2}} - \left(\frac{13}{4}\right)^{\frac{3}{2}}\right] \\ &= 27\left(80\sqrt{10} - 13\sqrt{13}\right)\end{align*}$$
연습문제1. 주어진 함수과 범위가 주어졌을 때 곡선의 길이를 구하는 공식을 세워라. 이때, 계산은 하지 않아도 된다.
(a). $y = \cos(x), 0 \le x \le 2\pi$
(b). $y = xe^{-x^{2}}, 0 \le x \le 1$
(c). $x = y + y^{3}, 1 \le y \le 4$
(d). $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$
(a). $y = \cos(x), 0 \le x \le 2\pi$
주어진 곡선의 미분은 $\frac{dy}{dx} = -\sin(x)$이므로 다음 식을 통해 곡선의 길이를 구할 수 있다.
$$\begin{align*} L &= \int_{0}^{2\pi} \sqrt{1 + \left( \frac{dy}{dx} \right)^{2}} \; dx \\ &= \int_{0}^{2\pi} \sqrt{1 + \sin^{2}(x)} \; dx \end{align*}$$
(b). $y = xe^{-x^{2}}, 0 \le x \le 1$
주어진 곡선의 미분은 $\frac{dy}{dx} = e^{-x^{2}} - 2x^{2}e^{-x^{2}} = (1 - 2x^{2})e^{-x^{2}}$이므로 다음 식을 통해 곡선의 길이를 구할 수 있다.
$$\begin{align*} L &= \int_{0}^{1} \sqrt{1 + \left( \frac{dy}{dx} \right)^{2}} \; dx \\ &= \int_{0}^{1} \sqrt{1 + \left( (1 - 2x^{2})e^{-x^{2}} \right)^{2}} \; dx \\ &= \int_{0}^{1} \sqrt{1 + (1 - 2x^{2})^{2}e^{-2x^{2}}} \; dx \end{align*}$$
(c). $x = y + y^{3}, 1 \le y \le 4$
주어진 곡선의 미분은 $\frac{dx}{dy} = 1 + 3y^{2}$이므로 다음 식을 통해 곡선의 길이를 구할 수 있다.
$$\begin{align*} L &= \int_{0}^{4} \sqrt{1 + \left( \frac{dx}{dy} \right)^{2}} \; dy \\ &= \int_{0}^{4} \sqrt{1 + \left( 1 + 3y^{2} \right)^{2}} \; dy \end{align*}$$
(d). $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$
주어진 곡선은 타원으로 폐곡선이다. 따라서, $0 \le x \le a$인 범위에서 곡선의 길이를 구한 뒤 4를 곱하면 된다. 주어진 곡선의 미분은 $\frac{2x}{a^{2}} + \frac{2y}{b^{2}} \frac{dy}{dx} = 0 \rightarrow \frac{dy}{dx} = -\frac{x}{y} \frac{b^{2}}{a^{2}}$이므로 다음 식을 통해 곡선의 길이를 구할 수 있다.
$$\begin{align*} L &= 4 \int_{0}^{a} \sqrt{1 + \left( \frac{dy}{dx} \right)^{2}} \; dx \\ &= 4\int_{0}^{a} \sqrt{1 + \left( - \frac{x}{y} \frac{b^{2}}{a^{2}} \right)^{2}} \; dx \\ &= 4\int_{0}^{a} \sqrt{1 + \frac{x^{2}}{y^{2}} \frac{b^{4}}{a^{4}}} \; dx \\ &= 4\int_{0}^{a} \sqrt{1 + \frac{x^{2}}{b^{2} - \frac{b^{2}}{a^{2}}x^{2}} \frac{b^{4}}{a^{4}}} \; dx \\ &= 4\int_{0}^{a} \sqrt{1 + \frac{x^{2}}{a^{2} - x^{2}} \frac{b^{2}}{a^{2}}} \; dx \end{align*}$$
연습문제2. 주어진 함수과 범위가 주어졌을 때 곡선의 길이를 구하여라.
(a). $y = 1 + 6x^{\frac{3}{2}}, 0 \le x \le 1$
(b). $y^{2} = 4(x + 4)^{3}, 0 \le x \le 2, y > 0$
(c). $y = \frac{x^{5}}{6} + \frac{1}{10x^{3}}, 1 \le x \le 2$
(d). $x = \frac{y^{4}}{8} + \frac{1}{4y^{2}}, 1 \le y \le 2$
(e). $x = \frac{1}{3}\sqrt{y}(y - 3), 1 \le y \le 9$
(a). $y = 1 + 6x^{\frac{3}{2}}, 0 \le x \le 1$
주어진 곡선의 미분은 $\frac{dy}{dx} = 6 \cdot \frac{3}{2} x^{\frac{1}{2}} = 9x^{\frac{1}{2}}$이므로 다음 식을 통해 곡선의 길이를 구할 수 있다.
$$\begin{align*} L &= \int_{0}^{1} \sqrt{1 + \left( \frac{dy}{dx} \right)^{2}} \; dx \\ &= \int_{0}^{1} \sqrt{1 + \left( 9x^{\frac{1}{2}} \right)^{2}} \; dx \\ &= \int_{0}^{1} \sqrt{1 + 81x} \; dx \\ &= \left[ \frac{1}{1 + \frac{1}{2}} \cdot \frac{1}{81} \cdot (1 + 81x)^{\frac{3}{2}} \right]_{0}^{1} \\ &= \frac{2}{243} \left[ (1 + 81x)^{\frac{3}{2}} \right]_{0}^{1} \\ &= \frac{2}{243} \left( 82\sqrt{82} - 1 \right) \end{align*}$$
(b). $y^{2} = 4(x + 4)^{3}, 0 \le x \le 2, y > 0$
주어진 곡선의 길이는 $y$가 양수인 영역만 구하면 된다. 주어진 곡선의 미분은 $2y\frac{dy}{dx} = 12(x + 4)^{2} \rightarrow \frac{dy}{dx} = \frac{6(x + 4)^{2}}{y} = \frac{6(x + 4)^{2}}{2(x + 4)^{\frac{3}{2}}} = 3(x + 4)^{\frac{1}{2}}$이므로 다음 식을 통해 곡선의 길이를 구할 수 있다.
$$\begin{align*} L &= \int_{0}^{2} \sqrt{1 + \left( \frac{dy}{dx} \right)^{2}} \; dx \\ &= \int_{0}^{2} \sqrt{1 + \left( 3(x + 4)^{\frac{1}{2}} \right)^{2}} \; dx \\ &= \int_{0}^{2} \sqrt{1 + 9(x + 4)} \; dx \\ &= \int_{0}^{2} \sqrt{37 + 9x} \; dx \\ &= \left[ \frac{1}{1 + \frac{1}{2}} \cdot \frac{1}{9} \cdot (37 + 9x)^{\frac{3}{2}} \right]_{0}^{2} \\ &= \frac{2}{27} \left[ (37 + 9x)^{\frac{3}{2}} \right]_{0}^{2} \\ &= \frac{2}{27} \left( 55\sqrt{55} - 37\sqrt{37} \right) \end{align*}$$
(c). $y = \frac{x^{5}}{6} + \frac{1}{10x^{3}}, 1 \le x \le 2$
주어진 곡선의 미분은 $\frac{dy}{dx} = \frac{5}{6}x^{4} - \frac{3}{10 x^{4}}$이므로 다음 식을 통해 곡선의 길이를 구할 수 있다.
$$\begin{align*} L &= \int_{1}^{2} \sqrt{1 + \left( \frac{dy}{dx} \right)^{2}} \; dx \\ &= \int_{1}^{2} \sqrt{1 + \left( \frac{5}{6}x^{4} - \frac{3}{10x^{4}} \right)^{2}} \; dx \\ &= \int_{1}^{2} \sqrt{1 + \left( \frac{25}{36}x^{8} + \frac{9}{100x^{8}} - \frac{1}{2} \right)} \; dx \\ &= \int_{1}^{2} \sqrt{\frac{25}{36} x^{8} + \frac{9}{100x^{8}} + \frac{1}{2}} \; dx \\ &= \int_{1}^{2} \sqrt{\left( \frac{5}{6}x^{4} + \frac{3}{10x^{4}} \right)^{2}} \; dx \\ &= \int_{1}^{2} \left( \frac{5}{6}x^{4} + \frac{3}{10x^{4}} \right) \; dx \\ &= \left[ \frac{1}{6}x^{5} - \frac{1}{10x^{3}} \right]_{1}^{2} \\ &= \left( \frac{32}{6} - \frac{1}{80} \right) - \left( \frac{1}{6} - \frac{1}{10} \right) = \frac{1261}{240} \end{align*}$$
(d). $x = \frac{y^{4}}{8} + \frac{1}{4y^{2}}, 1 \le y \le 2$
주어진 곡선의 미분은 $\frac{dx}{dy} = \frac{1}{2}y^{3} - \frac{1}{2y^{3}}$이므로 다음 식을 통해 곡선의 길이를 구할 수 있다.
$$\begin{align*} L &= \int_{1}^{2} \sqrt{1 + \left( \frac{dx}{dy} \right)^{2}} \; dy \\ &= \int_{1}^{2} \sqrt{1 + \left( \frac{1}{2}y^{3} - \frac{1}{2y^{3}} \right)^{2}} \; dy \\ &= \int_{1}^{2} \sqrt{1 + \left( \frac{1}{4}y^{6} + \frac{1}{4y^{6}} - \frac{1}{2} \right)} \; dx \\ &= \int_{1}^{2} \sqrt{\frac{1}{4} y^{6} + \frac{1}{4y^{6}} + \frac{1}{2}} \; dx \\ &= \frac{1}{2} \int_{1}^{2} \sqrt{\left( y^{3} + \frac{1}{y^{3}} \right)^{2}} \; dx \\ &= \frac{1}{2} \int_{1}^{2} \left( y^{3} + \frac{1}{y^{3}} \right) \; dx \\ &= \frac{1}{2} \left[ \frac{1}{4}y^{4} - \frac{1}{2y^{2}} \right]_{1}^{2} \\ &= \frac{1}{2} \left[ \left( 4 - \frac{1}{8} \right) - \left( \frac{1}{4} - \frac{1}{2} \right) \right] = \frac{33}{16} \end{align*}$$
(e). $x = \frac{1}{3}\sqrt{y}(y - 3), 1 \le y \le 9$
주어진 곡선의 미분은 $\frac{dx}{dy} = \frac{1}{3} \left( \frac{1}{2\sqrt{y}}(y - 3) + \sqrt{y} \right)$이므로 다음 식을 통해 곡선의 길이를 구할 수 있다.
$$\begin{align*} L &= \int_{1}^{9} \sqrt{1 + \left( \frac{dx}{dy} \right)^{2}} \; dy \\ &= \int_{1}^{9} \sqrt{1 + \frac{1}{9}\left( \frac{1}{2\sqrt{y}}(y - 3) - \sqrt{y} \right)^{2}} \; dy \\ &= \frac{1}{3} \int_{1}^{9} \sqrt{\frac{y}{4} + \frac{9}{4y} + \frac{9}{2}} \; dx \\ &= \frac{1}{3} \int_{1}^{9} \sqrt{\left( \frac{\sqrt{y}}{2} + \frac{3}{2\sqrt{y}} \right)^{2}} \; dx \\ &= \frac{1}{3} \int_{1}^{9} \left( \frac{\sqrt{y}}{2} + \frac{3}{2\sqrt{y}} \right) \; dx \\ &= \frac{1}{3} \left[ \frac{1}{2} \cdot \frac{2}{3} y^{\frac{3}{2}} - \frac{3}{2} \cdot 2 y^{\frac{1}{2}} \right]_{1}^{9} \\ &= \frac{1}{3} \left[ \frac{1}{3}y^{\frac{3}{2}} - 3y^{\frac{1}{2}} \right]_{1}^{9} \\ &= \frac{1}{3} \left[ \left( \frac{1}{3} \cdot 9\sqrt{9} - 3\sqrt{9} \right) - \left( \frac{1}{3} - 3 \right) \right] = \frac{8}{9} \end{align*}$$
연습문제3. 주어진 함수과 범위가 주어졌을 때 곡선의 길이를 구하여라.
(a). $y = \ln (\cos(x)), 0 \le x \le \frac{\pi}{3}$
(b). $y = \ln (\sec(x)), 0 \le x \le \frac{\pi}{4}$
(c). $y = 3 + \frac{1}{2}\cosh(2x), 0 \le x \le 1$
(d). $y = \ln (1 - x^{2}), 0 \le x \le \frac{1}{2}$
(e). $y = e^{x}, 0 \le x \le 1$
(a). $y = \ln (\cos(x)), 0 \le x \le \frac{\pi}{3}$
주어진 곡선의 미분은 $\frac{dy}{dx} = -\frac{\sin(x)}{\cos(x)} = -\tan(x)$이므로 다음 식을 통해 곡선의 길이를 구할 수 있다.
$$\begin{align*} L &= \int_{0}^{\frac{\pi}{3}} \sqrt{1 + \left( \frac{dy}{dx} \right)^{2}} \; dx \\ &= \int_{0}^{\frac{\pi}{3}} \sqrt{1 + \left( -\tan(x) \right)^{2}} \; dx \\ &= \int_{0}^{\frac{\pi}{3}} \sqrt{1 + \tan^{2}(x)} \; dx \\ &= \int_{0}^{\frac{\pi}{3}} \sqrt{\sec^{2}(x)} \; dx \\ &= \int_{0}^{\frac{\pi}{3}} \sec(x) \; dx \\ &= \left[ \ln \left( \sec(x) + \tan(x) \right) \right]_{0}^{\frac{\pi}{3}} \\ &= \ln (\sec(\frac{\pi}{3}) + \tan(\frac{\pi}{3})) - \ln (\sec(0) + \tan(0)) = \ln (2 + \sqrt{3}) \end{align*}$$
(b). $y = \ln (\sec(x)), 0 \le x \le \frac{\pi}{4}$
주어진 곡선의 미분은 $\frac{dy}{dx} = \frac{\sec(x)\tan(x)}{\sec(x)} = \tan(x)$이므로 다음 식을 통해 곡선의 길이를 구할 수 있다.
$$\begin{align*} L &= \int_{0}^{\frac{\pi}{4}} \sqrt{1 + \left( \frac{dy}{dx} \right)^{2}} \; dx \\ &= \int_{0}^{\frac{\pi}{4}} \sqrt{1 + \left( \tan(x) \right)^{2}} \; dx \\ &= \int_{0}^{\frac{\pi}{4}} \sqrt{1 + \tan^{2}(x)} \; dx \\ &= \int_{0}^{\frac{\pi}{4}} \sqrt{\sec^{2}(x)} \; dx \\ &= \int_{0}^{\frac{\pi}{4}} \sec(x) \; dx \\ &= \left[ \ln \left( \sec(x) + \tan(x) \right) \right]_{0}^{\frac{\pi}{4}} \\ &= \ln (\sec(\frac{\pi}{4}) + \tan(\frac{\pi}{4})) - \ln (\sec(0) + \tan(0)) = \ln (\sqrt{2} + 1) \end{align*}$$
(c). $y = 3 + \frac{1}{2}\cosh(2x), 0 \le x \le 1$
주어진 곡선의 미분은 $\frac{dy}{dx} = \sinh(2x)$이므로 다음 식을 통해 곡선의 길이를 구할 수 있다.
$$\begin{align*} L &= \int_{0}^{1} \sqrt{1 + \left( \frac{dy}{dx} \right)^{2}} \; dx \\ &= \int_{0}^{1} \sqrt{1 + \left( \sinh(2x) \right)^{2}} \; dx \\ &= \int_{0}^{1} \sqrt{1 + \sinh^{2}(2x)} \; dx \\ &= \int_{0}^{1} \sqrt{\cosh^{2}(2x)} \; dx \\ &= \int_{0}^{1} \cosh(2x) \; dx \\ &= \frac{1}{2} \left[ \sinh(2x) \right]_{0}^{1} \\ &= \frac{1}{2} \left( \sinh(2) - \sinh(0) \right) = \frac{1}{2} \sinh(2) \end{align*}$$
(d). $y = \ln (1 - x^{2}), 0 \le x \le \frac{1}{2}$
주어진 곡선의 미분은 $\frac{dy}{dx} = -\frac{2x}{1 - x^{2}}$이므로 다음 식을 통해 곡선의 길이를 구할 수 있다.
$$\begin{align*} L &= \int_{0}^{\frac{1}{2}} \sqrt{1 + \left( \frac{dy}{dx} \right)^{2}} \; dx \\ &= \int_{0}^{\frac{1}{2}} \sqrt{1 + \left( -\frac{2x}{1 - x^{2}} \right)^{2}} \; dx \\ &= \int_{0}^{\frac{1}{2}} \sqrt{\frac{(1 + x^{2})^{2}}{(1 - x^{2})^{2}}} \; dx \\ &= \int_{0}^{\frac{1}{2}} \sqrt{\left( \frac{1 + x^{2}}{1 - x^{2}} \right)^{2}} \; dx \\ &= \int_{0}^{\frac{1}{2}} \frac{1 + x^{2}}{1 - x^{2}} \; dx \\ &= \int_{0}^{\frac{1}{2}} \left( \frac{1}{x + 1} - \frac{1}{x - 1} - 1 \right) \; dx \\ &= \left[ \ln \left| \frac{x + 1}{x - 1} \right| - x \right]_{0}^{\frac{1}{2}} \\ &= \ln 3 - \frac{1}{2} \end{align*}$$
(e). $y = e^{x}, 0 \le x \le 1$
주어진 곡선의 미분은 $\frac{dy}{dx} = e^{x}$이므로 다음 식을 통해 곡선의 길이를 구할 수 있다.
$$\begin{align*} L &= \int_{0}^{1} \sqrt{1 + \left( \frac{dy}{dx} \right)^{2}} \; dx \\ &= \int_{0}^{1} \sqrt{1 + \left( e^{x} \right)^{2}} \; dx \\ &= \int_{0}^{1} \sqrt{1 + e^{2x}} \; dx \end{align*}$$
이제, $e^{x} = u$라고 하면 $e^{x} dx = du \rightarrow dx = \frac{1}{e^{x}} du = \frac{1}{u} du$이고 적분구간은 $[0, 1] \rightarrow [1, e]$이다. 따라서, 다음과 같이 치환적분을 수행할 수 있다.
$$\begin{align*} L &= \int_{0}^{1} \sqrt{1 + \left( \frac{dy}{dx} \right)^{2}} \; dx \\ &= \int_{0}^{1} \sqrt{1 + e^{2x}} \; dx \\ &= \int_{1}^{e} \sqrt{1 + u^{2}} \cdot \frac{1}{u} \; du \\ &= \int_{1}^{e} \frac{\sqrt{1 + u^{2}}}{u} \; du \end{align*}$$
이제, $u = \sinh(v)$라고 하면 $du = \cosh(v) dv$이고 적분구간은 $[1, e] \rightarrow [\text{arcsinh}(1), \text{arcsinh}(e)]$이다. 따라서, 다음과 같이 치환적분을 수행할 수 있다.
$$\begin{align*} L &= \int_{0}^{1} \sqrt{1 + \left( \frac{dy}{dx} \right)^{2}} \; dx \\ &= \int_{1}^{e} \frac{\sqrt{1 + u^{2}}}{u} \; du \\ &= \int_{\text{arcsinh}(1)}^{\text{arcsinh}(e)} \frac{\sqrt{1 + \sinh^{2}(v)}}{\cosh(v)} \cdot \cosh(v) \; dv \\ &= \int_{\\text{arcsinh}(1)}^{\text{arcsinh}(e)} \cosh(v) \; dv \\ &= \left[ \sinh(v) \right]_{\text{arcsinh}(1)}^{\text{arcsinh}(e)} \\ &= \sinh(\text{arcsinh}(e)) - \sinh(\text{arcsinh}(1)) = e - 1 \end{align*}$$
참고자료 및 그림출처
Calculus(J. Stewart)
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 일 (1) | 2022.03.30 |
|---|---|
| 미적분학 - 회전체의 겉넓이 (2) | 2022.03.29 |
| 미적분학 - 특이적분 (0) | 2022.03.24 |
| 미적분학 - 적분 전략 (0) | 2022.03.24 |
| 미적분학 - 부분분수를 활용한 유리함수 적분 (0) | 2022.03.22 |
안녕하세요. 지난 포스팅의 미적분학 - 특이적분에서는 무한대가 포함된 구간의 적분과 불연속점에 포함된 피적분함수의 적분에 대해서 알아보았습니다. 핵심은 임의의 실수 t를 선택한 뒤 무한 또는 불연속점으로 극한을 취해주면 되었습니다. 이때, 항상 극한이 존재하는 것이 아니기 때문에 특이적분에서는 값이 존재하지 않을 수도 있습니다. 오늘은 적분의 새로운 응용으로 호의 길이를 구하는 방법에 대해서 알아보도록 하겠습니다.

위 그림과 같이 함수 y=f(x)가 있다고 가정하겠습니다. 저희가 원하는 것은 구간 [a,b]까지의 함수 f(x)의 자취인 곡선 C의 길이 L를 구하는 것입니다. 일단, 길이를 어떻게 구할 수 있는 지부터 생각해보겠습니다. 길이라는 것은 시작점과 끝점이 주어지며 두 점 사이의 거리를 의미합니다. 따라서, 곡선의 길이를 구하기 위해서는 시작점과 끝점을 정해야겠죠. 이를 P0와 Pn이라고 하겠습니다. 만약, n=1이라고 한다면, 구간 [a,b]를 그대로 쓰는 것으로 x0와 x1만 존재하는 것을 의미합니다. 좀 더 정확한 곡선의 길이를 구하기 위해서는 n을 늘리면 되겠죠? 따라서, 구간을 등구간 [xi−1,xi]으로 나누면 각 구간의 길이는 Δx가 됩니다. 그리고 이에 대응되는 곡선위의 점을 편의상 Pi(xi,yi)=Pi이라고 쓰겠습니다.

위 그림을 보시면 곡선 C의 길이는 다각형의 길이의 합으로 생각해볼 수 있습니다. 즉, ∑ni=1|Pi−1Pi|이죠. 이때, |Pi−1Pi|란 두 점 Pi−1과 Pi 사이의 길이를 의미합니다. 그리고 정확한 곡선의 길이 L은 n에 극한을 취해서 얻을 수 있습니다.
L=limn→∞n∑i=1|Pi−1Pi|
이제 저희가 할 일은 |Pi−1Pi|를 구하는 것입니다. 기본적으로 직교좌표 상에서 두 점 사이의 거리는 아래와 같습니다.
|Pi−1Pi|=√(xi−xi−1)2+(yi−yi−1)2=√(Δx)2+(Δy)2
이때, 중요한 점은 여기서 평균값 정리(Mean Value Theorem, MVT)를 활용해야합니다. 평균값 정리의 자세한 설명은 아래의 링크를 참조해주시길 바랍니다.
미적분학 - 평균값 정리
안녕하세요. 지난 포스팅의 미적분학 - 최대값과 최소값에서는 전역최대 및 전역최소의 정의, 그리고 지역최대 및 지역최소의 정의, 마지막으로 임계값에 대해서 알아보았습니다. 그리고 이와
everyday-image-processing.tistory.com
Δy=yi−yi−1=f(xi)−f(xi−1)=f∗(x′i)(xi−xi−1)=f′(x∗i)Δx
따라서, 저희는 기존의 식을 아래와 같이 바꿀 수 있습니다.
|Pi−1Pi|=√(xi−xi−1)2+(yi−yi−1)2=√(Δx)2+(Δy)2=√(Δx)2+(f′(x∗i)Δx)2=√1+[f′(x∗i)]2Δx
그러므로 저희가 원하는 곡선의 길이 L은 아래와 같습니다.
L=limn→∞n∑i=1|Pi−1Pi|=limn→∞n∑i=1√1+[f′(x∗i)]Δx=∫ba√1+[f′(x)]2dx
예제1. 두 점 (1,1)과 (4,8)사이의 포물선 y2=x3의 길이를 구하여라.
y2=x3⇒y=x32이기 때문에 미분하면 dydx=32x12이다. 이제, 곡선의 길이를 구하기 위해 공식을 적용한다.
L=∫41√1+94xdx
여기서 1+94x=u라고 하면 x=1→u=134,x=4→u=10이고 94dx=du⇒dx=49du이기 때문에 아래와 같이 치환적분이 가능하다.
L=∫41√1+94xdx=∫10134√u(49du)=49∫10134√udu=49[23u32]10134=827[1032−(134)32]=27(80√10−13√13)
연습문제1. 주어진 함수과 범위가 주어졌을 때 곡선의 길이를 구하는 공식을 세워라. 이때, 계산은 하지 않아도 된다.
(a). y=cos(x),0≤x≤2π
(b). y=xe−x2,0≤x≤1
(c). x=y+y3,1≤y≤4
(d). x2a2+y2b2=1
(a). y=cos(x),0≤x≤2π
주어진 곡선의 미분은 dydx=−sin(x)이므로 다음 식을 통해 곡선의 길이를 구할 수 있다.
L=∫2π0√1+(dydx)2dx=∫2π0√1+sin2(x)dx
(b). y=xe−x2,0≤x≤1
주어진 곡선의 미분은 dydx=e−x2−2x2e−x2=(1−2x2)e−x2이므로 다음 식을 통해 곡선의 길이를 구할 수 있다.
L=∫10√1+(dydx)2dx=∫10√1+((1−2x2)e−x2)2dx=∫10√1+(1−2x2)2e−2x2dx
(c). x=y+y3,1≤y≤4
주어진 곡선의 미분은 dxdy=1+3y2이므로 다음 식을 통해 곡선의 길이를 구할 수 있다.
L=∫40√1+(dxdy)2dy=∫40√1+(1+3y2)2dy
(d). x2a2+y2b2=1
주어진 곡선은 타원으로 폐곡선이다. 따라서, 0≤x≤a인 범위에서 곡선의 길이를 구한 뒤 4를 곱하면 된다. 주어진 곡선의 미분은 2xa2+2yb2dydx=0→dydx=−xyb2a2이므로 다음 식을 통해 곡선의 길이를 구할 수 있다.
L=4∫a0√1+(dydx)2dx=4∫a0√1+(−xyb2a2)2dx=4∫a0√1+x2y2b4a4dx=4∫a0√1+x2b2−b2a2x2b4a4dx=4∫a0√1+x2a2−x2b2a2dx
연습문제2. 주어진 함수과 범위가 주어졌을 때 곡선의 길이를 구하여라.
(a). y=1+6x32,0≤x≤1
(b). y2=4(x+4)3,0≤x≤2,y>0
(c). y=x56+110x3,1≤x≤2
(d). x=y48+14y2,1≤y≤2
(e). x=13√y(y−3),1≤y≤9
(a). y=1+6x32,0≤x≤1
주어진 곡선의 미분은 dydx=6⋅32x12=9x12이므로 다음 식을 통해 곡선의 길이를 구할 수 있다.
L=∫10√1+(dydx)2dx=∫10√1+(9x12)2dx=∫10√1+81xdx=[11+12⋅181⋅(1+81x)32]10=2243[(1+81x)32]10=2243(82√82−1)
(b). y2=4(x+4)3,0≤x≤2,y>0
주어진 곡선의 길이는 y가 양수인 영역만 구하면 된다. 주어진 곡선의 미분은 2ydydx=12(x+4)2→dydx=6(x+4)2y=6(x+4)22(x+4)32=3(x+4)12이므로 다음 식을 통해 곡선의 길이를 구할 수 있다.
L=∫20√1+(dydx)2dx=∫20√1+(3(x+4)12)2dx=∫20√1+9(x+4)dx=∫20√37+9xdx=[11+12⋅19⋅(37+9x)32]20=227[(37+9x)32]20=227(55√55−37√37)
(c). y=x56+110x3,1≤x≤2
주어진 곡선의 미분은 dydx=56x4−310x4이므로 다음 식을 통해 곡선의 길이를 구할 수 있다.
L=∫21√1+(dydx)2dx=∫21√1+(56x4−310x4)2dx=∫21√1+(2536x8+9100x8−12)dx=∫21√2536x8+9100x8+12dx=∫21√(56x4+310x4)2dx=∫21(56x4+310x4)dx=[16x5−110x3]21=(326−180)−(16−110)=1261240
(d). x=y48+14y2,1≤y≤2
주어진 곡선의 미분은 dxdy=12y3−12y3이므로 다음 식을 통해 곡선의 길이를 구할 수 있다.
L=∫21√1+(dxdy)2dy=∫21√1+(12y3−12y3)2dy=∫21√1+(14y6+14y6−12)dx=∫21√14y6+14y6+12dx=12∫21√(y3+1y3)2dx=12∫21(y3+1y3)dx=12[14y4−12y2]21=12[(4−18)−(14−12)]=3316
(e). x=13√y(y−3),1≤y≤9
주어진 곡선의 미분은 dxdy=13(12√y(y−3)+√y)이므로 다음 식을 통해 곡선의 길이를 구할 수 있다.
L=∫91√1+(dxdy)2dy=∫91√1+19(12√y(y−3)−√y)2dy=13∫91√y4+94y+92dx=13∫91√(√y2+32√y)2dx=13∫91(√y2+32√y)dx=13[12⋅23y32−32⋅2y12]91=13[13y32−3y12]91=13[(13⋅9√9−3√9)−(13−3)]=89
연습문제3. 주어진 함수과 범위가 주어졌을 때 곡선의 길이를 구하여라.
(a). y=ln(cos(x)),0≤x≤π3
(b). y=ln(sec(x)),0≤x≤π4
(c). y=3+12cosh(2x),0≤x≤1
(d). y=ln(1−x2),0≤x≤12
(e). y=ex,0≤x≤1
(a). y=ln(cos(x)),0≤x≤π3
주어진 곡선의 미분은 dydx=−sin(x)cos(x)=−tan(x)이므로 다음 식을 통해 곡선의 길이를 구할 수 있다.
L=∫π30√1+(dydx)2dx=∫π30√1+(−tan(x))2dx=∫π30√1+tan2(x)dx=∫π30√sec2(x)dx=∫π30sec(x)dx=[ln(sec(x)+tan(x))]π30=ln(sec(π3)+tan(π3))−ln(sec(0)+tan(0))=ln(2+√3)
(b). y=ln(sec(x)),0≤x≤π4
주어진 곡선의 미분은 dydx=sec(x)tan(x)sec(x)=tan(x)이므로 다음 식을 통해 곡선의 길이를 구할 수 있다.
L=∫π40√1+(dydx)2dx=∫π40√1+(tan(x))2dx=∫π40√1+tan2(x)dx=∫π40√sec2(x)dx=∫π40sec(x)dx=[ln(sec(x)+tan(x))]π40=ln(sec(π4)+tan(π4))−ln(sec(0)+tan(0))=ln(√2+1)
(c). y=3+12cosh(2x),0≤x≤1
주어진 곡선의 미분은 dydx=sinh(2x)이므로 다음 식을 통해 곡선의 길이를 구할 수 있다.
L=∫10√1+(dydx)2dx=∫10√1+(sinh(2x))2dx=∫10√1+sinh2(2x)dx=∫10√cosh2(2x)dx=∫10cosh(2x)dx=12[sinh(2x)]10=12(sinh(2)−sinh(0))=12sinh(2)
(d). y=ln(1−x2),0≤x≤12
주어진 곡선의 미분은 dydx=−2x1−x2이므로 다음 식을 통해 곡선의 길이를 구할 수 있다.
L=∫120√1+(dydx)2dx=∫120√1+(−2x1−x2)2dx=∫120√(1+x2)2(1−x2)2dx=∫120√(1+x21−x2)2dx=∫1201+x21−x2dx=∫120(1x+1−1x−1−1)dx=[ln|x+1x−1|−x]120=ln3−12
(e). y=ex,0≤x≤1
주어진 곡선의 미분은 dydx=ex이므로 다음 식을 통해 곡선의 길이를 구할 수 있다.
L=∫10√1+(dydx)2dx=∫10√1+(ex)2dx=∫10√1+e2xdx
이제, ex=u라고 하면 exdx=du→dx=1exdu=1udu이고 적분구간은 [0,1]→[1,e]이다. 따라서, 다음과 같이 치환적분을 수행할 수 있다.
L=∫10√1+(dydx)2dx=∫10√1+e2xdx=∫e1√1+u2⋅1udu=∫e1√1+u2udu
이제, u=sinh(v)라고 하면 du=cosh(v)dv이고 적분구간은 [1,e]→[arcsinh(1),arcsinh(e)]이다. 따라서, 다음과 같이 치환적분을 수행할 수 있다.
L=∫10√1+(dydx)2dx=∫e1√1+u2udu=∫arcsinh(e)arcsinh(1)√1+sinh2(v)cosh(v)⋅cosh(v)dv=∫arcsinh(e)textarcsinh(1)cosh(v)dv=[sinh(v)]arcsinh(e)arcsinh(1)=sinh(arcsinh(e))−sinh(arcsinh(1))=e−1
참고자료 및 그림출처
Calculus(J. Stewart)
'수학 > 미적분학' 카테고리의 다른 글
| 미적분학 - 일 (1) | 2022.03.30 |
|---|---|
| 미적분학 - 회전체의 겉넓이 (2) | 2022.03.29 |
| 미적분학 - 특이적분 (0) | 2022.03.24 |
| 미적분학 - 적분 전략 (0) | 2022.03.24 |
| 미적분학 - 부분분수를 활용한 유리함수 적분 (0) | 2022.03.22 |
