안녕하세요. 지난 포스팅인 기초통계학[31].귀무가설의 유의성 검정 4에서는 $z$ 검정에 대해서 알아보았습니다. 오늘은 스튜던트 $t$ 검정에 대해서 알아보도록 하겠습니다. 하지만 스튜던트 $t$ 검정을 배우기 위해서 알아야하는 스튜던트 $t$ 분포부터 배우고 넘어가도록 하겠습니다.
여기서 $t$ 분포 앞에 붙은 "스튜던트"는 해당 분포를 제시한 윌리엄 고셋의 필명을 따서 지었습니다. 윌리엄 고셋은 양조장에서 일했다고 합니다. 그 이름도 유명한 기네스였습니다!! 양조장에서 맥주를 만들 때 사용되는 "홉"의 이상적인 비율을 알아내기 위해서 윌리엄 고셋이 직접 분포를 만들었습니다. 하지만, 자신의 이름으로 이와 관련된 논문을 학계에 내고자 했으나 기네스 측에서는 이를 받아주지 않았다고 합니다. 다만, ‘연구원 신분이 노출되지 않는 가명이라면 연구 내용을 발표해도 좋다’라는 기네스 측의 조건을 받아들여 필명을 통해 논문을 발표했다고 하였습니다.
1. $t$ 분포($t$ distribution)
여러분들 모두 여기까지 오셨다면 정규분포의 모양이 평균을 중심으로 종모양의 대칭형인 것을 기억하실 겁니다. $t$ 분포도 정규분포와 매우 유사합니다. 다른 점은 정규분포는 중심이 이동할 수 있지만 $t$ 분포는 중심이 항상 0으로 고정되어 있다는 것입니다. 그리고 정규분포는 분산의 크기에 따라서 중심을 기준으로 넓게 분포하거나 좁게 분포할 수도 있었습니다. $t$ 분포 역시 어떤 값을 기준으로 0을 중심으로 넓게 분포하거나 좁게 분포할 수도 있습니다. 그 값을 자유도(degree of freedom; df)라고 합니다. 여기서 자유도는 표본의 개수에 의존하는 값입니다. 만약 표본의 개수가 많아지면 $t$ 분포는 평균이 0이고 분산이 1인 표준정규분포와 모양이 유사해집니다. 또한, $t$ 분포는 표준정규분포에 비해서 꼬리 영역이 더 두껍다는 특징이 있습니다. 이것은 $t$ 분포를 따르는 데이터들은 중심에 덜 모여있다는 것을 의미합니다.
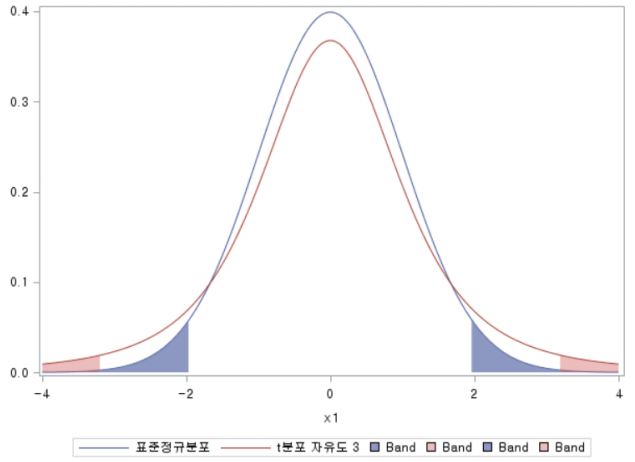
위의 그림을 보도록 하겠습니다. 파란색을 표준정규분포를 나타냅니다. 빨간색은 자유도가 3인 $t$ 분포를 나타내고 있습니다. 방금 언급한 것처럼 $t$ 분포의 꼬리 영역이 표준정규분포에 비해서 조금 더 두껍다는 것을 알 수 있습니다.
이제 검정을 중심으로 생각해보도록 하겠습니다. 각 확률밀도함수에서 색칠한 영역은 좌우 꼬리 영역 각각 2.5%를 의미합니다. 합쳐서 5%의 영역입니다. 표준정규분포의 경우에는 중심인 0에서 2정도만 벗어나도 다르다는 결과를 줄것입니다. 그에 반해 $t$ 분포의 경우에는 2를 벗어나더라도 같다는 결과를 줄것입니다. 이를 "보수적이다." 또는 "보수적인 검정이다."라고 표현합니다. 왜냐하면 꽤나 큰 차이가 없다면 다르다는 결과를 주지 않기 때문이죠.
사실 $t$ 분포를 더 정확하게 이해하기 위해서는 $\chi^{2}$ 분포를 이해해야합니다. 하지만 오늘은 그 느낌 정도만 알고 넘어가도록 하겠습니다.
2. $t$ 검정
일단 $t$ 검정에는 크게 2가지 종류가 존재합니다. 각각 일표본 $t$ 검정, 이표본 $t$ 검정이라고 부릅니다. 오늘은 이 두가지를 각각 배워보도록 하겠습니다.
2.1 일표본 $t$ 검정(one sample $t$ test)
다시 $z$ 검정 과정을 생각해보겠습니다. $z$ 검정 시 검정 통계량은 $Z = \frac{\bar{x}-\mu_{0}}{\frac{\sigma}{\sqrt{n}}}$으로 표준화(standardization)를 진행해야했습니다. 일표본 $t$ 검정도 마찬가지로 표본에 대해서 어떤 변환을 적용해야하는 데 이를 학생화(studentization)이라고 말합니다. "학생화"라고 부르는 이유는 위에서 언급했듯이 $t$ 분포를 제안한 윌리엄 고셋의 필명이 "학생(student)"이기 때문이죠. $z$ 검정에서 정리했던 것처럼 동일하게 정리하면 아래와 같습니다.
- 데이터 : $x_{1}, x_{2}, \dots, x_{n} \sim {N(\mu, \sigma^{2})}$이고 $\mu$와 $\sigma$는 모르는 값입니다.
- 귀무가설 $H_{0}$ : "어떤 값 $\mu_{0}$에 대해서 $\mu = \mu_{0}$이다."
- 검정 통계량 $t$ : $t = \frac{\bar{x} - \mu_{0}}{\frac{s}{\sqrt{n}}}$이고 이때, $s^{2} = \frac{1}{n-1}\sum_{i=1}^{n}{(x_{i} - \bar{x})^{2}}$으로 정의됩니다. 여기서 $t$는 학생화 평균, $s^{2}$은 표본 분산이라고 합니다. $s^{2}$같은 경우에는 실제 분산 $\sigma^{2}$의 추정치라고 보면 됩니다.
- 귀무분포 $f(t|H_{0})$ : 확률 변수 $T \sim {t(n - 1)}$의 확률 밀도함수입니다. 이때, $t(n-1)$에서 $t$는 $t$ 분포를 의미하고 $n-1$은 자유도를 의미합니다.
- 오른쪽 꼬리로 정의된 $p$ 값 : $p = P(T > t|H_{0})$
- 왼쪽 꼬리로 정의된 $p$ 값 : $p = P(T < t|H_{0})$
- 양쪽 꼬리로 정의된 $p$ 값 : $p = P(|T| > |t||H_{0})$
이제 일표본 $t$ 검정을 활용해서 NHST를 진행해보도록 하겠습니다. 여기서 사용할 예제는 이전 포스팅의 예제1을 사용하는 데 다만, 분산 $\sigma$도 모른다고 가정하겠습니다. 이전 예제와 동일하게 저희는 데이터 1, 2, 3, 6, -1을 얻었다고 가정하겠습니다.
먼저 귀무가설 $H_{0}$를 "$\mu = 0$이다."라고 정의하겠습니다. 그리고 대립가설 $H_{A}$는 $\mu > 0$이 될 것입니다. 그리고 유의 수준 $\alpha = 0.05$라고 가정하겠습니다. 그러면 귀무가설 $H_{0}$를 기각할 수 있을 까요?
일표본 $t$ 검정을 사용하기 위해서는 표본에 대한 평균인 $\bar{x}$를 구해야합니다. 그러면 $\bar{x} = 2.2$가 됩니다. 또한, 데이터의 가정에 의해서 각각의 데이터는 어떤 $\mu$, $\sigma$를 가지는 정규분포를 따를 것입니다. 이때, $\mu$, $\sigma$는 저희가 모르는 값이기 때문에 일표본 $t$ 검정을 사용할 수 있습니다.
다음으로 표본 분산 $s^{2}$을 계산해야합니다. 이는 위의 계산식을 참고하여 아래와 같이 계산하면 됩니다.
$$s^{2} = \frac{1}{4} ((1 - 2.2)^{2} + (2 - 2.2)^{2} + (3 - 2.2)^{2} + (6 - 2.2)^{2} + (-1 - 2.2)^{2}) = 6.7$$
따라서, 저희의 검정 통계량 $t$는 $\frac{\bar{x} - \mu_{0}}{\frac{s}{\sqrt{n}}} = \frac{2.2}{\frac{\sqrt{6.7}}{\sqrt{5}}} = 1.901$가 되는 것을 알 수 있습니다. 대립가설 $H_{A}$를 보면 오른쪽 꼬리로 정의되었습니다. 그러므로 $p$ 값은 아래와 같이 유도할 수 있습니다.
$$p = P(T > t) = P(T > 1.901)$$
자 그럼 이제 $P(T > 1.901)$만 얻으면 됩니다. 하지만 $T$가 정규분포가 아니라 $t$ 분포를 따르기 때문에 정규분포표가 아닌 $t$ 분포표를 보고 얻어야합니다. 아래의 표를 참조해보세요.
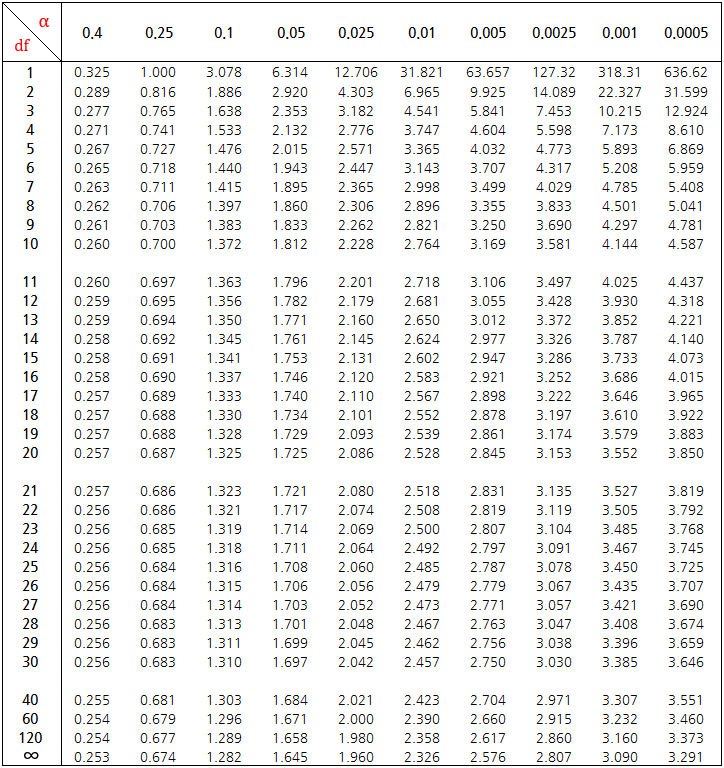
y축은 자유도를 의미합니다. 표본의 개수에서 1을 뺀 값이죠. 그리고 x축은 확률을 의미합니다. 그리고 표안의 숫자가 $t$ 값을 의미합니다. 하지만, 위의 표를 통해서 $P(T > 1.901)$을 찾을 수는 없습니다... 왜냐하면 1.901에 해당하는 $t$ 값이 없기 때문이죠. 다만, 유의 수준 $\alpha$가 0.05이고 자유도가 4일 때의 $t$ 값은 2.132인것은 알 수 있습니다. 이제, $P(T > 1.901)$을 구하는 방법은 통계학에서 자주 사용되는 언어인 R을 이용해야합니다. 그러면, 아래와 같이 쉽게 값을 구할 수 있습니다.
$$P(T > 1.901) = 1 - pt(1.901, 4) = 0.065$$
이때, $pt(1.901, 4)$는 자유도 4일 때의 $t$ 분포에서 $P(T < 1.901)$인 확률을 찾는 것과 동일합니다. 그러면 $p$ 값이 0.065인 것을 알았으며 이를 유의 수준 $\alpha$와 비교해보면 $p$ 값이 더 큰 것을 알 수 있습니다. 그러므로 귀무가설을 기각하지 않습니다. 이것을 그림으로 그리면 아래와 같습니다.
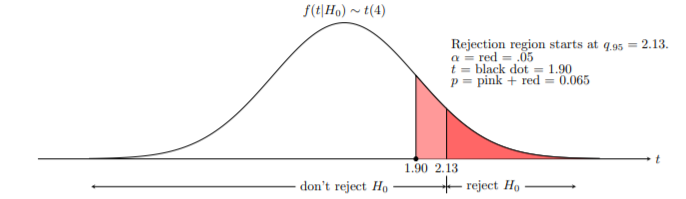
2.2 이표본 $t$ 검정(two-sample $t$ test)
다음으로 볼 것은 이표본 $t$ 검정입니다. 일표본 $t$ 검정에서는 데이터의 표본이 1개의 세트밖에 없었습니다. 그에 반해 이표본 $t$ 검정에서는 데이터의 표본이 2개의 세트가 존재합니다. 일표본 $t$ 검정과 비교해보며 보시면 더 쉽게 이해할 수 있을 것입니다.
- 데이터 : 표본 집합 $x_{1}, x_{2}, \dots, x_{n} \sim {N(\mu_{1}, \sigma^{2})}$라고 하고, 다른 표본 집합은 $y_{1}, y_{2}, \dots, y_{m} \sim {N(\mu_{2}, \sigma^{2})}$이라고 가정하겠습니다. 이때, 각각의 $\mu_{1}, \mu_{2}, \sigma$는 알지못하는 값입니다. 여기서 중요하게 봐야할 것은 두 데이터 표본의 분산이 동일하다는 점입니다. 그리고 첫번째 표본 집합은 $n$개의 데이터를 가지는 데 반해, 두번째 표본 집합은 $m$개의 데이터를 가지고 있습니다. 즉, 굳이 두 표본 집합의 개수가 동일할 필요가 없다는 것을 의미합니다.
- 귀무가설 $H_{0}$ : $\mu_{1} = \mu_{2}$
- 검정 통계량 $t$ : $t = \frac{\bar{x} - \bar{y}}{s_{p}}$이고 여기서 $s^{2}_{p} = \frac{(n - 1)s^{2}_{x} + (m - 1)s^{2}_{y}}{n + m - 2}(\frac{1}{n} + \frac{1}{m})$입니다. 그리고 $s^{2}_{x}, s^{2}_{y}$는 각각 $x_{i}, y_{j}$의 표본 분산을 의미합니다.
- 귀무분포 $f(t|H_{0})$ : 확률 변수 $T \sim {t(n + m - 2)}$의 확률 밀도함수입니다.
- 오른쪽 꼬리로 정의된 $p$ 값 : $p = P(T > t|H_{0})$
- 왼쪽 꼬리로 정의된 $p$ 값 : $p = P(T < t|H_{0})$
- 양쪽 꼬리로 정의된 $p$ 값 : $p = P(|T| > |t| | H_{0})$
일표본 $t$ 검정과 비교해보면 그렇게 큰 차이가 있지 않다는 것을 알 수 있습니다. 바뀐 것은 귀무가설, 검정 통계량밖에 없습니다!! 마지막으로 이표본 $t$ 검정을 위한 예제를 확인하고 끝내도록 하겠습니다.
예제1. 본 예제는 해당 여성들이 1). 의학적인 이유로 또는 2). 예약되지 않은 응급 상황으로 인해서 임산부 병원에 입원한 1408명의 여성을 대상으로 한 데이터입니다. 임신 기간은 마지막 생리 기간이 시작된 후 완전히 끝난 주에 측정이 됩니다. 데이터 요약을 하자면 아래와 같습니다.
- 의학적인 이유로 입원한 경우 : 755명의 환자. 해당 환자들의 임신 기간 평균 $\bar{x}_{M} = 39.08$, 분산은 $s^{2}_{M} = 7.77$
- 응급 상황으로 입원한 경우 : 633명의 환자. 해당 환자들의 임신 기간 평균 $\bar{y}_{E} = 39.60$, 분산은 $s^{2}_{E} = 4.95$
이제 이표본 $t$ 검정을 통해서 두 환자 그룹의 평균이 다른 지 확인해보도록 하겠습니다. 먼저, 검정 통계량을 계산하기 위해서 $s^{2}_{p}$를 계산해야합니다. 이는 값들이 전부 평균과 분산으로 주어져있기 때문에 쉽게 계산할 수 있습니다. 그 결과, $s^{2}_{p} = \frac{39.08 \times 7.77 + 39.60 \times 4.95}{755 + 633 - 2}(\frac{1}{755} + \frac{1}{633}) = 0.0187$입니다.
이제, 검정 통계량을 구하면 $t = \frac{\bar{x}_{M} - \bar{y}_{E}}{s_{p}} = \frac{39.08 - 39.60}{\sqrt{0.0187}} = -3.8064$가 됩니다. 이때, 대립가설 $H_{A}$를 보도록 하겠습니다. 단순히 크다, 작다가 아닌 평균이 다른 지이므로 $\mu_{1} \neq \mu_{2}$입니다. 따라서 양쪽 꼬리로 정의된 $p$ 값을 구해야함을 알 수 있습니다. 그러므로 $p = P(|T| > 3.8064)$를 계산하면 됩니다. 이는 R을 이용하면 0.00015라는 값을 쉽게 구할 수 있습니다.(이때, 자유도가 1406인것을 있지 마세요!!!)
$p$ 값을 보면 자주 쓰이는 유의 수준인 0.05, 0.001 보다도 훨씬 작은 것을 알 수 있습니다. 따라서 저희는 귀무가설 $H_{0}$를 기각하고 대립가설 $H_{A}$를 선택할 수 있습니다. 그러므로 두 환자 그룹의 평균이 다르다는 결론을 내릴 수 있습니다.
'수학 > 기초통계학' 카테고리의 다른 글
| 기초통계학[34].베이즈 추론과 빈도주의 추론의 비교 (0) | 2020.08.06 |
|---|---|
| 기초통계학[33].귀무가설의 유의성 검정 6 (0) | 2020.08.05 |
| 기초통계학[31].귀무가설의 유의성 검정 4 (0) | 2020.07.21 |
| 기초통계학[30].귀무가설의 유의성 검정 3 (0) | 2020.07.17 |
| 기초통계학[29].귀무가설의 유의성 검정 2 (0) | 2020.07.16 |
안녕하세요. 지난 포스팅인 기초통계학[31].귀무가설의 유의성 검정 4에서는 $z$ 검정에 대해서 알아보았습니다. 오늘은 스튜던트 $t$ 검정에 대해서 알아보도록 하겠습니다. 하지만 스튜던트 $t$ 검정을 배우기 위해서 알아야하는 스튜던트 $t$ 분포부터 배우고 넘어가도록 하겠습니다.
여기서 $t$ 분포 앞에 붙은 "스튜던트"는 해당 분포를 제시한 윌리엄 고셋의 필명을 따서 지었습니다. 윌리엄 고셋은 양조장에서 일했다고 합니다. 그 이름도 유명한 기네스였습니다!! 양조장에서 맥주를 만들 때 사용되는 "홉"의 이상적인 비율을 알아내기 위해서 윌리엄 고셋이 직접 분포를 만들었습니다. 하지만, 자신의 이름으로 이와 관련된 논문을 학계에 내고자 했으나 기네스 측에서는 이를 받아주지 않았다고 합니다. 다만, ‘연구원 신분이 노출되지 않는 가명이라면 연구 내용을 발표해도 좋다’라는 기네스 측의 조건을 받아들여 필명을 통해 논문을 발표했다고 하였습니다.
1. $t$ 분포($t$ distribution)
여러분들 모두 여기까지 오셨다면 정규분포의 모양이 평균을 중심으로 종모양의 대칭형인 것을 기억하실 겁니다. $t$ 분포도 정규분포와 매우 유사합니다. 다른 점은 정규분포는 중심이 이동할 수 있지만 $t$ 분포는 중심이 항상 0으로 고정되어 있다는 것입니다. 그리고 정규분포는 분산의 크기에 따라서 중심을 기준으로 넓게 분포하거나 좁게 분포할 수도 있었습니다. $t$ 분포 역시 어떤 값을 기준으로 0을 중심으로 넓게 분포하거나 좁게 분포할 수도 있습니다. 그 값을 자유도(degree of freedom; df)라고 합니다. 여기서 자유도는 표본의 개수에 의존하는 값입니다. 만약 표본의 개수가 많아지면 $t$ 분포는 평균이 0이고 분산이 1인 표준정규분포와 모양이 유사해집니다. 또한, $t$ 분포는 표준정규분포에 비해서 꼬리 영역이 더 두껍다는 특징이 있습니다. 이것은 $t$ 분포를 따르는 데이터들은 중심에 덜 모여있다는 것을 의미합니다.

위의 그림을 보도록 하겠습니다. 파란색을 표준정규분포를 나타냅니다. 빨간색은 자유도가 3인 $t$ 분포를 나타내고 있습니다. 방금 언급한 것처럼 $t$ 분포의 꼬리 영역이 표준정규분포에 비해서 조금 더 두껍다는 것을 알 수 있습니다.
이제 검정을 중심으로 생각해보도록 하겠습니다. 각 확률밀도함수에서 색칠한 영역은 좌우 꼬리 영역 각각 2.5%를 의미합니다. 합쳐서 5%의 영역입니다. 표준정규분포의 경우에는 중심인 0에서 2정도만 벗어나도 다르다는 결과를 줄것입니다. 그에 반해 $t$ 분포의 경우에는 2를 벗어나더라도 같다는 결과를 줄것입니다. 이를 "보수적이다." 또는 "보수적인 검정이다."라고 표현합니다. 왜냐하면 꽤나 큰 차이가 없다면 다르다는 결과를 주지 않기 때문이죠.
사실 $t$ 분포를 더 정확하게 이해하기 위해서는 $\chi^{2}$ 분포를 이해해야합니다. 하지만 오늘은 그 느낌 정도만 알고 넘어가도록 하겠습니다.
2. $t$ 검정
일단 $t$ 검정에는 크게 2가지 종류가 존재합니다. 각각 일표본 $t$ 검정, 이표본 $t$ 검정이라고 부릅니다. 오늘은 이 두가지를 각각 배워보도록 하겠습니다.
2.1 일표본 $t$ 검정(one sample $t$ test)
다시 $z$ 검정 과정을 생각해보겠습니다. $z$ 검정 시 검정 통계량은 $Z = \frac{\bar{x}-\mu_{0}}{\frac{\sigma}{\sqrt{n}}}$으로 표준화(standardization)를 진행해야했습니다. 일표본 $t$ 검정도 마찬가지로 표본에 대해서 어떤 변환을 적용해야하는 데 이를 학생화(studentization)이라고 말합니다. "학생화"라고 부르는 이유는 위에서 언급했듯이 $t$ 분포를 제안한 윌리엄 고셋의 필명이 "학생(student)"이기 때문이죠. $z$ 검정에서 정리했던 것처럼 동일하게 정리하면 아래와 같습니다.
- 데이터 : $x_{1}, x_{2}, \dots, x_{n} \sim {N(\mu, \sigma^{2})}$이고 $\mu$와 $\sigma$는 모르는 값입니다.
- 귀무가설 $H_{0}$ : "어떤 값 $\mu_{0}$에 대해서 $\mu = \mu_{0}$이다."
- 검정 통계량 $t$ : $t = \frac{\bar{x} - \mu_{0}}{\frac{s}{\sqrt{n}}}$이고 이때, $s^{2} = \frac{1}{n-1}\sum_{i=1}^{n}{(x_{i} - \bar{x})^{2}}$으로 정의됩니다. 여기서 $t$는 학생화 평균, $s^{2}$은 표본 분산이라고 합니다. $s^{2}$같은 경우에는 실제 분산 $\sigma^{2}$의 추정치라고 보면 됩니다.
- 귀무분포 $f(t|H_{0})$ : 확률 변수 $T \sim {t(n - 1)}$의 확률 밀도함수입니다. 이때, $t(n-1)$에서 $t$는 $t$ 분포를 의미하고 $n-1$은 자유도를 의미합니다.
- 오른쪽 꼬리로 정의된 $p$ 값 : $p = P(T > t|H_{0})$
- 왼쪽 꼬리로 정의된 $p$ 값 : $p = P(T < t|H_{0})$
- 양쪽 꼬리로 정의된 $p$ 값 : $p = P(|T| > |t||H_{0})$
이제 일표본 $t$ 검정을 활용해서 NHST를 진행해보도록 하겠습니다. 여기서 사용할 예제는 이전 포스팅의 예제1을 사용하는 데 다만, 분산 $\sigma$도 모른다고 가정하겠습니다. 이전 예제와 동일하게 저희는 데이터 1, 2, 3, 6, -1을 얻었다고 가정하겠습니다.
먼저 귀무가설 $H_{0}$를 "$\mu = 0$이다."라고 정의하겠습니다. 그리고 대립가설 $H_{A}$는 $\mu > 0$이 될 것입니다. 그리고 유의 수준 $\alpha = 0.05$라고 가정하겠습니다. 그러면 귀무가설 $H_{0}$를 기각할 수 있을 까요?
일표본 $t$ 검정을 사용하기 위해서는 표본에 대한 평균인 $\bar{x}$를 구해야합니다. 그러면 $\bar{x} = 2.2$가 됩니다. 또한, 데이터의 가정에 의해서 각각의 데이터는 어떤 $\mu$, $\sigma$를 가지는 정규분포를 따를 것입니다. 이때, $\mu$, $\sigma$는 저희가 모르는 값이기 때문에 일표본 $t$ 검정을 사용할 수 있습니다.
다음으로 표본 분산 $s^{2}$을 계산해야합니다. 이는 위의 계산식을 참고하여 아래와 같이 계산하면 됩니다.
$$s^{2} = \frac{1}{4} ((1 - 2.2)^{2} + (2 - 2.2)^{2} + (3 - 2.2)^{2} + (6 - 2.2)^{2} + (-1 - 2.2)^{2}) = 6.7$$
따라서, 저희의 검정 통계량 $t$는 $\frac{\bar{x} - \mu_{0}}{\frac{s}{\sqrt{n}}} = \frac{2.2}{\frac{\sqrt{6.7}}{\sqrt{5}}} = 1.901$가 되는 것을 알 수 있습니다. 대립가설 $H_{A}$를 보면 오른쪽 꼬리로 정의되었습니다. 그러므로 $p$ 값은 아래와 같이 유도할 수 있습니다.
$$p = P(T > t) = P(T > 1.901)$$
자 그럼 이제 $P(T > 1.901)$만 얻으면 됩니다. 하지만 $T$가 정규분포가 아니라 $t$ 분포를 따르기 때문에 정규분포표가 아닌 $t$ 분포표를 보고 얻어야합니다. 아래의 표를 참조해보세요.

y축은 자유도를 의미합니다. 표본의 개수에서 1을 뺀 값이죠. 그리고 x축은 확률을 의미합니다. 그리고 표안의 숫자가 $t$ 값을 의미합니다. 하지만, 위의 표를 통해서 $P(T > 1.901)$을 찾을 수는 없습니다... 왜냐하면 1.901에 해당하는 $t$ 값이 없기 때문이죠. 다만, 유의 수준 $\alpha$가 0.05이고 자유도가 4일 때의 $t$ 값은 2.132인것은 알 수 있습니다. 이제, $P(T > 1.901)$을 구하는 방법은 통계학에서 자주 사용되는 언어인 R을 이용해야합니다. 그러면, 아래와 같이 쉽게 값을 구할 수 있습니다.
$$P(T > 1.901) = 1 - pt(1.901, 4) = 0.065$$
이때, $pt(1.901, 4)$는 자유도 4일 때의 $t$ 분포에서 $P(T < 1.901)$인 확률을 찾는 것과 동일합니다. 그러면 $p$ 값이 0.065인 것을 알았으며 이를 유의 수준 $\alpha$와 비교해보면 $p$ 값이 더 큰 것을 알 수 있습니다. 그러므로 귀무가설을 기각하지 않습니다. 이것을 그림으로 그리면 아래와 같습니다.

2.2 이표본 $t$ 검정(two-sample $t$ test)
다음으로 볼 것은 이표본 $t$ 검정입니다. 일표본 $t$ 검정에서는 데이터의 표본이 1개의 세트밖에 없었습니다. 그에 반해 이표본 $t$ 검정에서는 데이터의 표본이 2개의 세트가 존재합니다. 일표본 $t$ 검정과 비교해보며 보시면 더 쉽게 이해할 수 있을 것입니다.
- 데이터 : 표본 집합 $x_{1}, x_{2}, \dots, x_{n} \sim {N(\mu_{1}, \sigma^{2})}$라고 하고, 다른 표본 집합은 $y_{1}, y_{2}, \dots, y_{m} \sim {N(\mu_{2}, \sigma^{2})}$이라고 가정하겠습니다. 이때, 각각의 $\mu_{1}, \mu_{2}, \sigma$는 알지못하는 값입니다. 여기서 중요하게 봐야할 것은 두 데이터 표본의 분산이 동일하다는 점입니다. 그리고 첫번째 표본 집합은 $n$개의 데이터를 가지는 데 반해, 두번째 표본 집합은 $m$개의 데이터를 가지고 있습니다. 즉, 굳이 두 표본 집합의 개수가 동일할 필요가 없다는 것을 의미합니다.
- 귀무가설 $H_{0}$ : $\mu_{1} = \mu_{2}$
- 검정 통계량 $t$ : $t = \frac{\bar{x} - \bar{y}}{s_{p}}$이고 여기서 $s^{2}_{p} = \frac{(n - 1)s^{2}_{x} + (m - 1)s^{2}_{y}}{n + m - 2}(\frac{1}{n} + \frac{1}{m})$입니다. 그리고 $s^{2}_{x}, s^{2}_{y}$는 각각 $x_{i}, y_{j}$의 표본 분산을 의미합니다.
- 귀무분포 $f(t|H_{0})$ : 확률 변수 $T \sim {t(n + m - 2)}$의 확률 밀도함수입니다.
- 오른쪽 꼬리로 정의된 $p$ 값 : $p = P(T > t|H_{0})$
- 왼쪽 꼬리로 정의된 $p$ 값 : $p = P(T < t|H_{0})$
- 양쪽 꼬리로 정의된 $p$ 값 : $p = P(|T| > |t| | H_{0})$
일표본 $t$ 검정과 비교해보면 그렇게 큰 차이가 있지 않다는 것을 알 수 있습니다. 바뀐 것은 귀무가설, 검정 통계량밖에 없습니다!! 마지막으로 이표본 $t$ 검정을 위한 예제를 확인하고 끝내도록 하겠습니다.
예제1. 본 예제는 해당 여성들이 1). 의학적인 이유로 또는 2). 예약되지 않은 응급 상황으로 인해서 임산부 병원에 입원한 1408명의 여성을 대상으로 한 데이터입니다. 임신 기간은 마지막 생리 기간이 시작된 후 완전히 끝난 주에 측정이 됩니다. 데이터 요약을 하자면 아래와 같습니다.
- 의학적인 이유로 입원한 경우 : 755명의 환자. 해당 환자들의 임신 기간 평균 $\bar{x}_{M} = 39.08$, 분산은 $s^{2}_{M} = 7.77$
- 응급 상황으로 입원한 경우 : 633명의 환자. 해당 환자들의 임신 기간 평균 $\bar{y}_{E} = 39.60$, 분산은 $s^{2}_{E} = 4.95$
이제 이표본 $t$ 검정을 통해서 두 환자 그룹의 평균이 다른 지 확인해보도록 하겠습니다. 먼저, 검정 통계량을 계산하기 위해서 $s^{2}_{p}$를 계산해야합니다. 이는 값들이 전부 평균과 분산으로 주어져있기 때문에 쉽게 계산할 수 있습니다. 그 결과, $s^{2}_{p} = \frac{39.08 \times 7.77 + 39.60 \times 4.95}{755 + 633 - 2}(\frac{1}{755} + \frac{1}{633}) = 0.0187$입니다.
이제, 검정 통계량을 구하면 $t = \frac{\bar{x}_{M} - \bar{y}_{E}}{s_{p}} = \frac{39.08 - 39.60}{\sqrt{0.0187}} = -3.8064$가 됩니다. 이때, 대립가설 $H_{A}$를 보도록 하겠습니다. 단순히 크다, 작다가 아닌 평균이 다른 지이므로 $\mu_{1} \neq \mu_{2}$입니다. 따라서 양쪽 꼬리로 정의된 $p$ 값을 구해야함을 알 수 있습니다. 그러므로 $p = P(|T| > 3.8064)$를 계산하면 됩니다. 이는 R을 이용하면 0.00015라는 값을 쉽게 구할 수 있습니다.(이때, 자유도가 1406인것을 있지 마세요!!!)
$p$ 값을 보면 자주 쓰이는 유의 수준인 0.05, 0.001 보다도 훨씬 작은 것을 알 수 있습니다. 따라서 저희는 귀무가설 $H_{0}$를 기각하고 대립가설 $H_{A}$를 선택할 수 있습니다. 그러므로 두 환자 그룹의 평균이 다르다는 결론을 내릴 수 있습니다.
'수학 > 기초통계학' 카테고리의 다른 글
| 기초통계학[34].베이즈 추론과 빈도주의 추론의 비교 (0) | 2020.08.06 |
|---|---|
| 기초통계학[33].귀무가설의 유의성 검정 6 (0) | 2020.08.05 |
| 기초통계학[31].귀무가설의 유의성 검정 4 (0) | 2020.07.21 |
| 기초통계학[30].귀무가설의 유의성 검정 3 (0) | 2020.07.17 |
| 기초통계학[29].귀무가설의 유의성 검정 2 (0) | 2020.07.16 |
