안녕하세요. 지난 포스팅 기초통계학[28].귀무가설의 유의성 검정 1에서는 NHST와 관련된 몇 가지 정의들을 활용해서 현실 문제에 통계학적인 언어로 쓸 수 있는 방법에 대해서 알아보았습니다. 오늘은 이에 이어서 좀 더 이론적인 배경에 대해서 설명하도록 하겠습니다.
저희가 귀무가설을 정의하게 되면 귀무가설에 맞다고 했을 때 정의되는 귀무분포를 얻을 수 있다는 것에서 시작합니다. 일반적으로 그 귀무분포는 정확하게(specific) 얻을 수 있는 경우는 많이 없습니다. 하지만 바로 이전 포스팅에서와 같이 간단한 귀무가설을 정하게 되면 이항분포를 통해서 정확하게 구할 수 있었습니다. 이와같이 가설에 대한 분포를 정확하게 구할 수 있는 가설을 "간단한 가설(simple hypothesis)" 이라고 합니다. 그에 반해, 정확하게 얻을 수 없는 경우 "복합 가설(composite hypothesis)" 이라고 합니다.
이전 포스팅의 예시를 생각해보겠습니다. 저희는 귀무가설을 "동전이 공평하다.", 즉 $\theta = 0.5$로 정의하였습니다. 이 경우에는 귀무분포를 정확하게 얻을 수 있으므로 $H_{0}$은 간단한 가설이 될 것입니다. 이에 반해 대립가설은 "동전이 공평하지 않다.". 즉, $\theta \neq 0.5$가 됩니다. 이 경우 그 확률분포를 특정하기 어렵기 때문에 $H_{A}$은 복합 가설이 됩니다. 왜냐하면 $\theta = 0.5000001, 0.499999$와 같은 값이 될 수도 있기 때문이죠.
다른 예시를 보도록 하겠습니다. 저희에게 $n$개의 데이터 $X_{n} = \{x_{1}, x_{2}, \dots, x_{n}\}$이 있다고 가정하겠습니다. 그리고 귀무가설 $H_{0}$를 "$X_{n}$이 $N(0, 1)$을 따른다."라고 하고, 대립가설 $H_{A}$를 "$X_{n}$이 $N(1, 1)$을 따른다."라고 하게 되면 귀무가설과 대립가설 모두 가우스 분포로 특정할 수 있기 때문에 둘 다 간단한 가설이 됩니다.
1. 1종 오류와 2종 오류
만약 귀무가설이 참인데 기각시키거나, 귀무가설이 거짓인데 기각을 하지 못하는 경우에 대한 오류를 의미합니다. 이들을 각각 1종 오류, 2종 오류라고 합니다.
2. 유의 수준(significance level)과 검정력(power)
유의 수준과 검정력은 유의성 검정의 품질을 정량화하는 데 사용됩니다. 즉, 이 유의성 검정이 얼마나 정확한지에 대해서 설명하는 측도라고 보면 될 거 같습니다. 정말 이상적으로 생각했을 때는 유의성 검정은 어떠한 오류도 발생해서는 안됩니다. 즉, 귀무가설 $H_{0}$가 참일 때 $H_{0}$를 기각해서는 안되며, $H_{A}$가 참일 때 $H_{0}$를 기각하고 $H_{A}$를 선택해야합니다. 이를 각각 조건부 확률로 쓰면 아래와 같습니다.
- $P(reject\ H_{0} | H_{0})$ : $H_{0}$가 참일 때 $H_{0}$가 기각될 확률
- $P(reject\ H_{0} | H_{A})$ : $H_{A}$가 참일 때 $H_{0}$가 기각될 확률
- $P(no\ reject\ H_{0} | H_{0})$ : $H_{0}$가 참일 때 $H_{0}$가 기각되지 않을 확률
- $P(no\ reject\ H_{0} | H_{A})$ : $H_{A}$가 참일 때 $H_{0}$가 기각되지 않을 확률
위에서 유의 수준은 첫번째 조건부 확률로 정의됩니다. 그리고 이는 1종 오류가 발생활 확률과 동일합니다. 그 이유는 조건부 확률을 재해석해보면 알 수 있습니다. 첫번째 조건부 확률이 "$H_{0}$가 참일 때 $H_{0}$가 기각될 확률"이라고 하였습니다. 그런데 이는 1종 오류의 정의와 완전히 동일하기 때문입니다.
그리고 검정력은 두번째 조건부 확률로 정의됩니다. 이는 $1 - P(2종\ 오류가\ 발생할\ 확률)$과 동일합니다. 그 이유는 두번째 조건부 확률이 "$H_{A}$가 참일 때 $H_{0}$가 기각될 확률"인데 이것은 2종 오류의 여집합과 동일한 개념일 같기 때문입니다.
그래서 이상적인 유의성 검정은 유의 수준을 최소화 하고, 검정력을 최대화해야합니다. 각각 0, 1로 다가가야하는 것이죠.
이제 예시를 보고 확인해보도록 하겠습니다. 이 예시는 이전 포스팅과 동일합니다.
동전이 공평한지 확인해보기 위해서 10번 던졌다고 가정하겠습니다. 만약 앞면이나 뒷면이 극단적으로 적거나 크다면 저희는 그 동전이 불공평하다고 의심할 것입니다. 예를 들어서 10번 중에서 앞면이 1번 나오거나, 9번 나오는 경우가 있겠죠. 이를 NHST를 사용하기 위한 언어로 바꾸는 과정이 필요합니다.
이 경우 대립가설 $H_{A}$는 복합 가설이라고 언급하였습니다. 따라서 검정력은 $\theta$의 값에 따라 달라질 것이라고 쉽게 유추할 수 있습니다. 그렇다면 실제로 $\theta$의 값을 조금씩 바꾸어가며 어떤 식으로 변화가 일어나는 지 확인해보도록 하겠습니다. 아래의 표를 참고해주세요.

이제 위의 확률 분포표를 활용해서 유의 수준과 각 $\theta$ 값에 따른 검정력을 알 수 있습니다.
- 유의 수준 = $H_{0}$가 참일 때 $H_{0}$를 기각할 확률이므로 이는 $H_{0}$가 참일 때 기각 영역안에 시험 통계량이 포함될 확률과 동일함을 알 수 있습니다. 즉, 상단의 표에서 빨간색 영역의 확률의 합으로 정의됩니다. 그러므로 0.11이 유의 수준이 됩니다.
- $\theta = 0.6$일 때 검정력 = $\theta = 0.6$일 때 $H_{0}$가 기각될 확률이므로 이는 $\theta = 0.6$일 때 기각 영역안에 시험 통계량이 포함될 확률과 동일함을 알 수 있습니다. 즉, 노란색 영역의 확률의 합으로 정의됩니다. 그러므로 0.180이 검정력이 됩니다.
- $\theta = 0.7$일 때 검정력 = $\theta = 0.7$일 때 $H_{0}$가 기각될 확률이므로 이는 $\theta = 0.7$일 때 기각 영역안에 시험 통계량이 포함될 확률과 동일함을 알 수 있습니다. 즉, 초록색 영역의 확률의 합으로 정의됩니다. 그러므로 0.384이 검정력이 됩니다.
위 결과를 보면 $\theta = 0.7$일 때의 검정력이 $\theta = 0.6$일 때의 검정력보다 더 큰 것을 알 수 있습니다. 검정력이 더 크다는 것은 대립가설과 귀무가설 사이의 차이가 크다는 것을 의미합니다. 실제로 $\theta = 0.6$일 때의 대립가설 보다는 $\theta = 0.7$일 때의 대립가설이 귀무가설과의 차이가 더 크기 때문에 검정력이 더 높은 것을 알 수 있습니다.
지금까지 정리한 결과로 몇 가지 결론을 얻을 수 있습니다.
- 기각 영역은 귀무 분포의 중심으로부터 멀리 떨어져있습니다.
- 기각 영역은 2개의 영역으로 이루어져있습니다.
- 대립가설은 귀무가설의 기각 여부에 영향을 주지 않습니다. 다시 한번 생각해보면 귀무가설의 기각 여부는 귀무가설이 맞다고 가정했을 때 그 우도의 값으로만 판단했습니다.
- 귀무가설은 증명될 수 없습니다. 단지, 주어진 데이터를 바탕으로 합리적인 추론을 하는 것뿐입니다.
3. 높은 검정력과 낮은 검정력
방금 말씀드린 검정력을 다시 떠올려보겠습니다. "검정력이 높다." = "대립가설과 귀무가설 사이의 차이가 크다." 라는 것을 알게 되었습니다. 그러므로 아래의 그림을 얻을 수 있습니다.
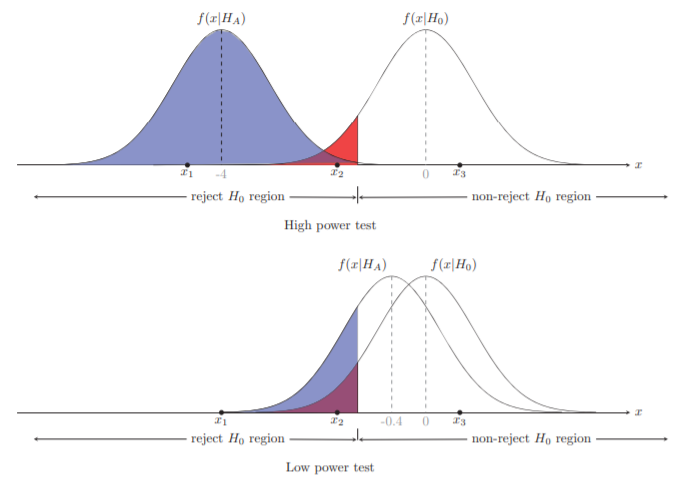
검정력은 $H_{A}$가 참일 때 $H_{0}$를 기각할 확률이라고 하였습니다. 이는 올바르게 기각한 것으로 $H_{A}$가 참일 때 $H_{0}$를 기각하지 않는 2종 오류의 여집합입니다. 따라서 1 - 2종 오류가 발생할 확률이라고 정의하였죠. 그림을 보면 높은 검정력을 가지는 상단의 그림은 귀무분포와 대립분포 사이의 평균이 멉니다. 그에 반해 낮은 검정력을 가지는 하단의 그림은 귀무분포와 대립분포 사이의 평균이 상대적으로 가깝습니다.
그리고 조건부 귀무분포 $f(x|H_{0})$에서 빨간색 영역이 유의 수준입니다. 다시 한번 유의 수준에 대해서 복습하면 1종 오류가 날 확률로써 귀무가설 $H_{0}$가 참이지만 기각할 확률이라고 했습니다.
다시 한번 위의 그림을 보면 파란색 영역을 볼 수 있습니다. 이 영역이 각 대립가설에 의한 검정력을 의미합니다. 왜냐하면 검정력은 $H_{A}$가 참이라고 가정했을 때 검정 통계량 $X$이 $H_{0}$의 기각 영역에 있을 확률과 동일하기 때문입니다. 유의 수준은 어차피 한번 정해진 귀무가설에 의한 귀무분포로 정해지기 때문에 위의 그림이나 아래의 그림이나 동일한 유의 수준을 가집니다. 하지만 검정력의 경우에는 귀무분포와 대립분포와 겹치면 겹칠수록 점점 커지는 작아지는 것을 알 수 있습니다.
예를 들어서 신약이 위약 효과에 의한 것인지, 아니면 정말 효과가 있는 것인지 알아보기 위한 검정을 수행한다고 가정해겠습니다. 이 경우 귀무가설 $H_{0}$는 "신약이 위약 효과보다 효과가 없다."라고 하겠습니다. 그리고 대립가설 $H_{A}$는 "신약이 위약 효과보다 효과가 있다."라고 하겠습니다. 이때, 가설 검정의 검정력은 "신약이 실제로 더 좋으면(대립가설이 맞다고 가정했을 때) 효과가 있다."라는 결론을 내릴 확률로 생각할 수 있습니다.(검정력의 정의를 다시 한번 생각해보세요.) 이에 반해 유의 수준은 "신약이 실제로 효과가 없을 때(귀무가설이 맞다고 가정했을 때) 효과가 있다."라는 결론을 내릴 확률로 생각할 수 있습니다.(유의 수준의 정의를 다시 한번 생각해보세요.)
'수학 > 기초통계학' 카테고리의 다른 글
| 기초통계학[31].귀무가설의 유의성 검정 4 (1) | 2020.07.21 |
|---|---|
| 기초통계학[30].귀무가설의 유의성 검정 3 (0) | 2020.07.17 |
| 기초통계학[28].귀무가설의 유의성 검정 1 (0) | 2020.07.14 |
| 기초통계학[27].빈도론자 관점의 통계학 (0) | 2020.07.11 |
| 기초통계학[26].예측 구간 (1) | 2020.07.10 |
