이번에는 여러 개의 파라미터를 가진 모델에 중에서 "올바른" 모델을 선택하고자 할 때의 설정을 다루어보도록 하겠습니다. 일단, "올바른" 모델이란 무엇일까요? 아마도 이는 상황과 목적에 따라 그 정의가 달라질 수 있습니다. 베이지안 결정이론은 이를 명확하게 정해줍니다.
두 개의 가설(일반적으로 모델을 지칭), 즉 귀무가설(null hypothesis) $M_{0}$과 대립가설(alternative hypothesis) $M_{1}$이 있고 그중 어느 쪽이 더 그럴듯한지 알고 싶다고 가정하겠습니다. 이를 가설검정(hypothesis testing)이라고 합니다.
지난 포스팅에서 보았던 0-1 손실을 쓴다고 가정하겠습니다. 최적 의사결정은 $p(M_{1} \mid \mathcal{D}) > p(M_{0} \mid \mathcal{D})$일 때 $M_{1}$을 고르는 것입니다. 이에 대한 동치는 $\frac{p(M_{0} \mid \mathcal{D})}{p(M_{1} \mid \mathcal{D})} > 1$이면 됩니다. 균일 사전분포 $p(M_{0}) = p(M_{1}) = 0.5$라고 가정하면 의사결정 규칙은 $M_{1}$을 선택할 조건은 $\frac{p(\mathcal{D} \mid M_{1})}{p(\mathcal{D} \mid M_{1})} > 1$이 됩니다. 이 식에서 주변우도(marginal likelihood)의 비를 베이즈 요인(Bayes factor)라고 부릅니다.
$$B_{1, 0} = \frac{p(\mathcal{D} \mid M_{1})}{p(\mathcal{D} \mid M_{0})}$$
이는 우도비(likelihood ratio)와 유사하지만 모델들의 파라미터를 적분으로 제거한다는 점이 다릅니다. 향후에 설명할 베이지안 오컴의 면도날(Bayesian Occam’s razor) 효과로 복잡도가 다른 모델도 비교할 수 있게 됩니다. $B_{1, 0} > 1$라면 모델 1을 선택하고 그렇지 않으면 모델 0을 선택하면 됩니다.
그렇다면 $B_{1, 0} = 1.0001$이나 $B_{1, 0} = 0.0009$와 같이 애매한 경우는 어떤 식으로 해석해야할까요? 이때는 모델 1이나 모델 0이 더 낫다는 확신을 크지 않다고 해석해야합니다.

Jeffreys라는 통계학자는 베이즈 요인의 크기를 해석하기 위한 증거 척도를 제안하기도 하였습니다. 이는 빈도주의 관점에서 바라본 $p$-값과 대응되는 베이지안 관점에서의 대안입니다.
간단한 예시를 들어 베이즈 요인을 계산해보겠습니다. 동전이 공평한 지 확인해보는 문제입니다. $M_{0}$을 공정한 동전으로 데이터 우도는 항상 $\left( \frac{1}{2} \right)^{N}$이 되고 $M_{1}$은 편향된 동전으로 $\theta$를 적분으로 평균낸 주변 우도 $p(\mathcal{D} \mid M_{1})$은 다음과 같습니다.
$$p(\mathcal{D} \mid M_{1}) = \int p(\mathcal{D} \mid \theta) p(\theta) \; d\theta = \frac{B(\alpha_{1} + N_{1}, \alpha_{0} + N_{0})}{B(\alpha_{1}, \alpha_{0})}$$
좀 더 문제를 쉽게 하기 위해 $\alpha_{0} = \alpha_{1} = 1$이라고 가정하면 $p(\mathcal{D} \mid M_{1})$은 다음과 같습니다.
$$p(\mathcal{D} \mid M_{1}) = \frac{B(N_{1} + 1, N_{0} + 1)}{B(1, 1)} = B(N_{1} + 1, N_{0} + 1)$$
이는 극단적인 결과(앞면이 거의 0이거나 거의 $N$)일수록 더 커지고 균형(50:50)일 수록 점점 작아지게 됩니다. 이는 “정말로 편향됐다면 극단 결과가 더 그럴듯”하다는 직관과 일치하게 됩니다.
만약, $N = 5$인 경우를 보도록 하겠습니다. 그러면 $p(\mathcal{D} \mid M_{0}) = \left( \frac{1}{2} \right)^{5} \approx 0.03125$가 됩니다. 여기서 $p(\mathcal{D} \mid M_{1})$의 경우 앞면이 나온 횟수 $N_{1}$에 따라 그 결과가 달라지게 됩니다.
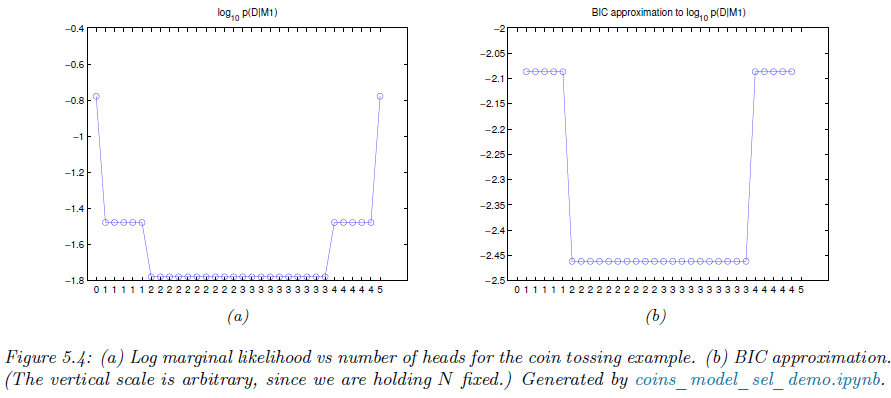
그림 5.4를 보도록 하겠습니다. 결국 2 ~ 3번의 앞면이 나오게 되었다면 균형에 가까우므로 $M_{0}$이 더 타당하게 되고 반대로 앞면이 아예 안나오거나 뒷면만 나온다면 극단적이므로 $M_{1}$이 좀 더 말이 됩니다.
