두 모델 $m_{1}$과 $m_{2}$가 있다고 가정하겠습니다. 여기서 $m_{1}$은 단순한 모델이고 $m_{2}$는 $m_{1}$보다는 더 복잡한 모델입니다. 두 모델 모두 적절한 파라미터 $\hat{\theta}_{1}$과 $\hat{\theta}_{2}$를 찾으면 데이터에 잘 맞는다고 가정하겠습니다. 즉, $p(\mathcal{D} \mid \hat{\theta}_{1}, m_{1})$과 $p(\mathcal{D} \mid \hat{\theta}_{2}, m_{2})$ 모두 크다고 가정하는 것이죠. 이 경우 단순한 모델인 $m_{1}$을 선택하는 것이 직관적으로 옳은 선택입니다. 이 원칙을 오컴의 면도날(Occam's razor)라고 부르죠. 즉, “같은 설명력을 가진다면 더 단순한 모델을 선택하라”는 의미입니다.
지난 포스팅에서 보았듯이 다양한 모델들이 있을 때 주변우도를 기반으로 최적의 모델을 선택하는 방식을 보았습니다. 이와 같이 모델의 순위를 주변우도로 매긴다면 자연스럽게 이 현상이 발생하게 됩니다. 일단, 복잡한 모델 $m_{2}$은 파라미터 공간이 넓기 때문에 좋은 파라미터 $\hat{\theta}_{2}$에 할당되는 사전 확률이 작습니다. 사전 확률은 전체 파라미터 공간에 대해서 적분했을 때 1이 되어야하므로 많은 부분에서 낮은 우도를 가지게 될 것 입니다. 반대로 단순한 모델 $m_{1}$의 경우 파라미터 공간이 상대적으로 좁을 것 입니다. 따라서, 사전 확률이 좋은 파라미터 주변에 더 집중되어 평균적으로 더 높은 우도를 얻게 됩니다. 결과적으로 주변우도는 더 단순한 모델을 선택하게 되죠. 이러한 현상을 베이지안 오컴의 면도날 효과(Bayesian Occam’s razor effect)이라고 합니다.
이 현상을 이해하는 또 다른 방법은 예측 능력의 분포를 비교하는 것입니다. 기본적으로 모든 가능한 데이터셋 $\mathcal{D}^{'}$에 대한 확률의 합은 1이어야합니다. 즉, $\sum_{\mathcal{D}^{'}} p(\mathcal{D}^{'} \mid m) = 1$이여야하죠. 여기서, 복잡한 모델은 예측할 수 있는 경우의 수가 많으므로, 각 데이터셋에 할당되는 확률 질량이 얇게 퍼집니다. 특정 데이터셋에는 높은 확률을 주기 어렵습니다. 반면에 단순한 모델은 예측 범위가 좁기 때문에, 특정 데이터셋(특히 관측된 데이터)에 더 높은 확률을 할당할 수 있습니다.
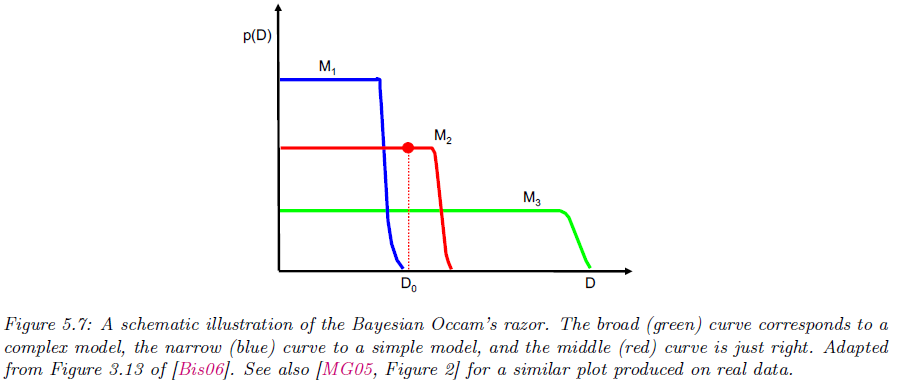
그림 5.7을 통해서 이 현상을 이해해보겠습니다. 여기서 $x$축은 가능한 모든 데이터셋을 복잡도 순서로 정렬해 놓은 축입니다. 그리고 $y$축은 어떤 모델 $M$이 각 데이터에 할당하는 예측 확률 $p(\mathcal{D} \mid M)$의 크기를 의미합니다. 이 그림을 연속 곡선처럼 보이지만 실제로는 가능한 데이터셋들의 집합 $\{ \mathcal{D}^{'} \}$위에서 $\sum_{\mathcal{D}^{'}} p(\mathcal{D}^{'} \mid m) = 1$이 할당되도록 확률 질량을 배분하고 있다는 것을 보여주고 있습니다.
이 그림에서 파란색 선인 $M_{1}$은 단순한 모델로 폭이 매우 좁고 높이가 큽니다. 이는 소수의 아주 단순한 데이터셋에 확률에 집중한다는 것을 보여주죠. 관측 데이터 $\mathcal{D}_{0}$가 파란 곡선의 급격한 하강 이후에 위치하므로 $p(\mathcal{D}_{0} \mid M_{1})$에 대해서는 과소적합이 발생했다고 볼 수 있습니다.
반면에 초록색 선인 $M_{3}$은 복잡한 모델로 폭이 매우 넓지만 높이는 낮습니다. 이는 많은 데이터를 설명할 수 있지만 확률 질량이 넓게 희석되죠. 그 결과 관측 데이터 $\mathcal{D}_{0}$에 대해서도 $p(\mathcal{D}_{0} \mid M_{3})$가 낮게 됩니다. 이는 과도한 유연성으로 인해 확률이 분산되었다고 볼 수 있죠.
마지막으로 빨간색 선인 $M_{2}$는 중간정도의 복잡한 모델로 폭과 높이가 모두 적당합니다. 지나치게 많은 데이터셋에 대해서 확률을 뿌리지도 많으며 너무 좁게도 한정하지 않습니다. 이로 인해 빨간 점이 관측 데이터 $\mathcal{D}_{0}$에 대해서도 $p(\mathcal{D}_{0} \mid M_{2})$가 최적이 됩니다.
이 그림에서 핵심적으로 전달하고자 하는 바는 베이지안 모델 비교는 기본적으로 주변우도 $p(\mathcal{D} \mid M) = \int p(\mathcal{D} \mid \theta, M) p(\theta \mid M) \; d\theta$를 통해 수행합니다. 여기서 복잡한 모델은 파라미터 공간이 더 넓어지게 되어 $p(\theta \mid M)$를 덜 좋은 영역에도 골고루 깔리게 됩니다. 이로 인해 평균(위에서 적분은 곧 평균임을 인지하세요.)을 취하면 낮은 우도 영역의 영향도 함께 적용되어 증거가 깍이는 효과가 발생합니다. 반대로 단순한 모델은 좋은 영역 근처에 사전이 상대적으로 집중되어 평균 우도가 유리해집니다.
