이번에는 두 개 이상의 모델이 포함된 집합 $\mathcal{M}$ 중에서 어떤 모델이 가장 그럴듯한 선택인지 다루어보도록 하겠습니다. 이 과정으로 모델 선택(Model Selection)이라고 부릅니다. 이를 의사결정 관점에서 해석해본다면 우리가 해야 할 행동은 여러 모델들 중 하나를 선택하는 것이죠, 즉, $m \in \mathcal{M}$을 선택하는 문제라고 볼 수 있습니다.
여기서는 0-1 손실을 사용했을 때의 최적 선택을 알아보도록 하겠습니다. 이 경우에는 확률이 가장 높은 모델을 고르는 것이 최적의 전략입니다.
$$\hat{m} = \text{argmax}_{m \in \mathcal{M}} p(m \mid \mathcal{D})$$
여기서 $p(m \mid \mathcal{D})$는 사후확률로 다음과 같이 계산됩니다.
$$p(m \mid \mathcal{D})= \frac{p(\mathcal{D} \mid m)p(m)}{\sum_{m^{'} \in \mathcal{M}} p(\mathcal{D} \mid m^{'})p(m^{'})}$$
이때, 모델에 대한 사전 확률이 균등분포라고 가정하겠습니다. 즉, $p(m) = \frac{1}{|M|}$이라고 하겠습니다. 그러면 MAP 추정은 사후 확률 대신 주변우도가 가장 큰 모델을 고르는 것과 동일하므로 다음과 같이 쓸 수 있습니다.
$$\hat{m} = \text{argmax}_{m \in \mathcal{M}} p(\mathcal{D} \mid m)$$
이제 주변 우도를 계산해봐야겠죠? 여기서 주변우도는 $p(\mathcal{D} \mid m) = \int p(\mathcal{D} \mid \theta, m) p(\theta \mid m) \; d\theta$가 됩니다. 이 값은 모델 $m$에 대한 모든 파라미터 설정에 대해 데이터가 나올 확률을 평균낸 것 입니다. 단, 평균을 낼 때는 사전분포 $p(\theta \mid m)$으로 가중합니다.
만약 어떤 모델의 모든 파라미터 설정이 데이터에 높은 확률을 준다면, 해당 모델은 좋은 모델일 가능성이 높습니다. 즉, 단순히 특정 파라미터에서의 성능이 좋은 것이 아니라 전반적으로 안정적인 성능을 내는 모델을 선호하게 됩니다.
결국 베이지안 모델 선택은 단순히 데이터에 가장 잘 맞는 파라미터를 찾는 것이 아니라, 모델 전체의 평균적인 설명력을 평가하여 선택하는 방법입니다. 이때 핵심 개념이 바로 주변우도입니다. 간단한 예시를 들어보도록 하겠습니다. 1차원 다항 회귀를 예로 들고 3가지 모델을 확인해보도록 하겠습니다. 모델 1부터 모델 3까지 각각 1차 ~ 3차 다항식 모델이라고 가정하겠습니다. 즉, 모델 1은 직선, 모델 2은 포물선, 모델 3은 삼차곡선이 됩니다.
모델 사전 확률 $p(m)$은 이전과 동일하게 균등 분포를 사용하겠습니다. 즉, 세 모델이 사전적으로 모두 동일하다고 가정합니다. 회귀 계수에 대한 사전 분포 $p(\theta \mid m)$은 경험적 베이즈(Empirical Bayes) 방식으로 추정합니다. 이는 향후에 더 자세히 알아보도록 하죠. 각 모델의 주변우도를 계산하는 자세한 과정 역시 향후에 더 자세하게 알아보겠습니다.
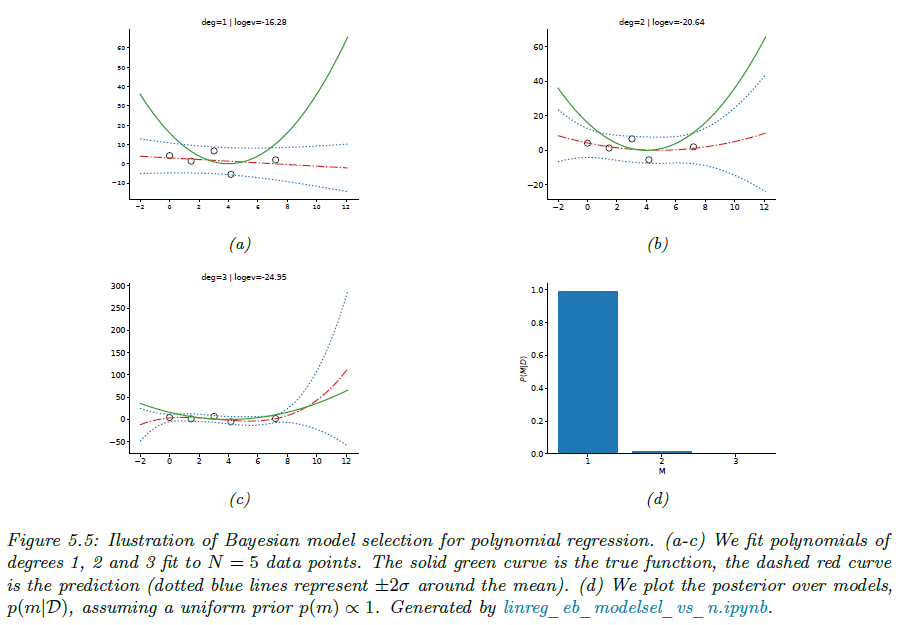
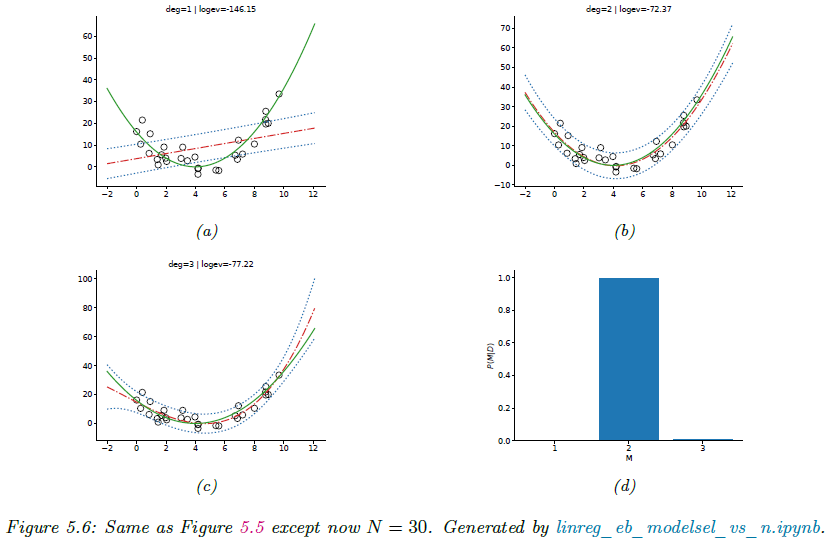
그림5.5는 데이터가 5개($N = 5$) 그리고 그림 5.6은 30개($N = 30$)인 경우 결과를 보여주고 있습니다. $N = 5$인 경우 데이터가 5개밖에 없기 때문에, 복잡한 모델을 선택할 근거가 충분하지 않습니다. 따라서 MAP 추정 결과, 최적 모델은 $m = 1$입니다. 반면에 $N = 30$인 경우 최적 모델은 $m = 2$가 됩니다. 즉, 표본 수가 증가하면 더 복잡한 모델을 선택할 근거가 제공되어 안전하게 선택할 수 있음을 보여주죠. 이는 데이터가 적을 때, 단순한 모델이 안정적이고 일반화 성능이 높으며 반대로 데이터가 많을 때, 더 많은 패턴을 포착할 수 있는 복잡한 모델을 선택 가능함을 볼 수 있습니다.
이러한 결과는 베이지안 모델 선택은 데이터 양에 따라 자연스럽게 모델 복잡도를 조절함을 보여주며 모델의 복잡성은 고정된 것이 아니라, 주어진 데이터 크기와 품질에 따라 달라진다는 것을 알려줍니다.
