이전 포스팅에서 저희는 거짓양성(False Positive)과 거짓음성(False Negative)의 상대적 비용으로부터 결정된 임곗값 $\tau$를 이용해 이진분류에서 최적의 레이블을 선택하는 방법에 대해서 알아보았습니다. 하지만 하나의 임곗값만 고집하기 보다는 여러 개의 임곗값을 시도해보고 그때마다 모델이 얼마나 잘 동작하는 지 비교할 수도 있습니다. 먼저, 임의의 고정된 임곗값 $\tau$에 대해서 저희는 다음과 같은 결정 규칙을 고려해볼 수 있습니다.
$$\hat{y}_{\tau}(\mathbf{x}) = \mathbb{I}(p(y = 1 \mid \mathbf{x}) \ge 1 - \tau)$$
즉, 양성일 확률이 $1 - \tau$보다 크다면 양성으로 예측하고 작다면 음성으로 예측하는 것이죠. 여기서 저희는 거짓양성인 FP를 계산해볼 수 있습니다.
$$\text{FP}_{\tau} = \sum_{n = 1}^{N} \mathbb{I}(\hat{y}_{\tau} (x_{n}) = 1, y_{n} = 0)$$
즉, 예측된 결과 $\hat{y}_{\tau} (x_{n})$는 양성(1)이지만 실제 레이블 $y_{n}$은 음성(0)인 케이스의 개수를 카운트한 것 입니다. 이와 같은 방식으로 거짓음성 FN, 참양성 TP, 참음성 TN에 해당하는 클래스의 개수를 모두 세볼 수 있습니다. 이를 기반으로 $2 \times 2$ 행렬로 만든 것이 바로 클래스 혼동 행렬 $C$입니다.
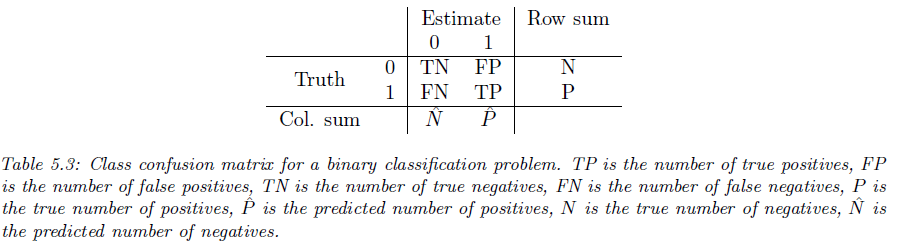
위 표 5.3으로부터 저희는 행 또는 열을 기준으로 정규화하면 $p(\hat{y} \mid y)$ 또는 $p(y \mid \hat{y})$와 같은 다양한 요약 통계를 얻을 수 있습니다.

표 5.4와 표 5.5가 그 예시를 보여주고 있스빈다. 예를 들어 민감도(Sensitivity), 재현율(Recall), 참양성비율(True Positive Rate; TPR)은 다음과 같이 구할 수 있습니다.
$$\text{TPR}_{\tau} = p(\hat{y} = 1 \mid y = 1, \tau) = \frac{\text{TP}_{\tau}}{\text{TP}_{\tau} + \text{FN}_{\tau}}$$
그리고 거짓 양성률(False Positive Rate; FPR), Type II Error는 다음과 같이 구할 수 있습니다.
$$\text{FPR}_{\tau} = p(\hat{y} = 1 \mid y = 0, \tau) = \frac{\text{FP}_{\tau}}{\text{FP}_{\tau} + \text{TN}_{\tau}}$$

마지막으로 TPR vs FPR을 임곗값 $\tau$에 따라서 그리면 그림 5.2 (a)와 같이 ROC 곡선(Receiver Operating Characteristic(ROC) Curve)를 얻을 수 있습니다. 이제 위 곡선으로부터 몇 가지 요약 통계를 더 얻을 수 있습니다.
- AUC(Area Under the Curve): 말 그대로 ROC 곡선의 밑 면적을 의미합니다. 이는 두 클래스 중 임의로 하나씩 뽑아서 점수를 비교했을 때 "양성 점수가 더 높다"라고 판단할 확률과 동일합니다. 0과 1 사이의 값으로 가지며 클수록 좋은 값입니다.
- EER(Equal Error Rate): 이는 거짓양성률(FPR)과 거짓음성률(FNR)이 같아지는 지점의 오류율을 의미합니다. 즉, FPR = FNR을 만족하는 것이죠? 따라서, FNR = 1 - TPR이 됩니다. 구하는 법은 간단합니다. ROC 곡선에서 좌상단에서 우하단으로 대각선을 하나 그어줍니다. 그 대각선과 ROC 곡선이 교차하는 지점의 x좌표가 바로 EER입니다. EER 역시 0과 1 사이의 값으로 작을수록 좋은 값 입니다.
몇몇 문제에서는 양성 샘플보다 음성 샘플이 훨씬 많은 상황이 있습니다. 예를 들어, 정보검색 시 관련 문서(양성)보다 무관한 문서(음성)가 훨씬 많은 경우가 있죠. ROC 곡선은 비율 지표이기 때문에 클래스 불균형 상황에서 큰 영향이 없습니다. 하지만, 음성이 너무 압도적으로 많다면 FP + TN도 너무 커져서 ROC 곡선의 좌측하단 구간만이 실제 차이를 보여주게 되고 나머지 구간은 모델 평가에 큰 정보를 주지 못합니다.
이를 대신해서 활용할 수 있는 다른 통계 기법이 그림 5.2 (b)에서 볼 수 있는 바로 정밀도-재현율 곡선(Precision-Recell Curve; PR Curve)입니다. 이에 대한 자세한 내용은 다음 포스팅에서 설명해보도록 하겠습니다.
