오늘 포스팅에서는 MVN을 기반으로한 선형 모델인 선형 가우시안 시스템(Linear Gaussian System; LGS)에 대해서 알아보도록 하겠스니다. 일단 모델을 가정하기 위해 잠재변수 $\mathbf{z} \in \mathbb{R}^{L}$이라고 하고 관측변수는 $\mathbf{y} \in \mathbb{R}^{D}$라고 하겠습니다. 그리고 추가적으로 이 변수들이 다음과 같은 관계식을 만족한다고 가정하겠습니다.
$$\begin{cases} p(\mathbf{z}) &= \mathcal{N}(\mathbf{z}|\mu_{z}, \Sigma_{z}) \\ p(\mathbf{y}|\mathbf{z}) &= \mathcal{N}(\mathbf{y}|\mathbf{W}\mathbf{z} + \mathbf{b}, \Sigma_{y}) \end{cases}$$
이때, $\mathbf{W} \in \mathbb{R}^{D \times L}$ 크기의 선형 변환 행렬입니다. 이러한 구조를 선형 가우시안 시스템이라고 부릅니다. 저희는 이전 포스팅에서도 보았다싶이 가우시안 분포를 따르는 두 변수의 결합분포 $p(\mathbf{z}, \mathbf{y}) = p(\mathbf{z})p(\mathbf{y}|\mathbf{z})$ 역시 가우시안임을 알았습니다. 그리고 그에 따른 차원은 $L + D$이죠. 그리고 결합분포에 대한 평균벡터 $\mu$와 공분산행렬 $\Sigma$는 다음과 같이 주어집니다.
$$\mu = \begin{pmatrix} \mu_{z} \\ \mathbf{W}\mu_{z} + \mathbf{b} \end{pmatrix}$$
$$\Sigma = \begin{pmatrix} \Sigma_{z} & \Sigma_{z}\mathbf{W}^{T} \\ \mathbf{W}^{T}\Sigma_{z} & \Sigma_{y} + \mathbf{W}\Sigma_{z}\mathbf{W}^{T} \end{pmatrix}$$
이제부터 저희는 관측값을 본 뒤의 사후분포 $p(\mathbf{z} | \mathbf{y})$를 유도할 것 입니다. 이는 "$\mathbf{z} \rightarrow \mathbf{y}$ 방향의 생성적 모델(generative model)을 관측 후 역전하여 잠재 변수 $\mathbf{z}$에 대한 불확실성을 업데이트"하는 과정으로 해석할 수 있습니다.
일단 선형 가우시안 시스템의 결합분포 $p(\mathbf{z}, \mathbf{y})$을 구해두었기 때문에 새로운 관측 $\mathbf{y}$를 본 뒤 잠재 변수 $\mathbf{z}$의 사후분포를 바로 쓸 수 있습니다.
$$\begin{cases} p(\mathbf{z}|\mathbf{y}) &= \mathcal{N}(\mathbf{z}|\mu_{z|y}, \Sigma_{z|y}) \\ \mu_{z|y} &= \Sigma_{z|y}\left[ \mathbf{W}^{T}\Sigma_{y}^{-1} (\mathbf{y} - \mathbf{b}) + \Sigma_{z}^{-1} \mu_{z} \right] \\ \Sigma^{-1}_{z|y} &= \Sigma^{-1}_{z} + \mathbf{W}^{T}\Sigma_{y}^{-1}\mathbf{W} \end{cases}$$
이 결과가 보통 가우시안에 대한 베이즈 룰로 알려져 있습니다. 그리고 사후분포의 정규화상수는 다음과 같이 계산됩니다.
$$p(\mathbf{y}) = \int \mathcal{N}(\mathbf{z}|\mu_{z}, \Sigma_{z})\mathbf{N}(\mathbf{y}|\mathbf{W}\mathbf{z} + \mathbf{b}, \Sigma_{y}) \; d\mathbf{z} = \mathcal{N}(\mathbf{y}|\mathbf{W}\mu_{z} + \mathbf{b}, \Sigma_{y} + \mathbf{W}\Sigma_{z}\mathbf{W}^{T})$$
즉, 선형 변환과 가우시안 합성은 여전히 가우시안 형태를 유지합니다. 이 결과로 알 수 있는 사실은 가우시안 사전분포 $p(\mathbf{z})$와 가우시안 우도 $p(\mathbf{y}|\mathbf{z})$를 곱해 정규화상수 $p(\mathbf{y})$로 나누어도 사후분포도 여전히 가우시안이라는 점 입니다. 일반적으로 이와 같은 같은 분포족(Distribution Family)로 사후분포가 복구되기 때문에 가우시안 분포는 가우시안 우도에 대한 공액 사전(Conjugate Prior)라고 합니다. 덕분에 선형 회귀, 칼만 필터, 가우시안 프로세스 회귀 등 다양한 모델에서 수식만으로 업데이트가 가능해 계산이 매우 간단해집니다. 이 부분에 대한 자세한 내용은 향후에 더 자세히 다루도록 하겠습니다. 몇 가지 예시를 들어서 설명드리기 전에 위 결과에 대한 실제 유도 과정을 아래에 정리하였으니 필요하신 분은 한번씩 봐주세요.
위 수식의 핵심 아이디어는 1) 결합분포 $p(\mathbf{z}, \mathbf{y}) = p(\mathbf{z})p(\mathbf{y}|\mathbf{z})$를 전개한 뒤, 2) 가우시안 조건화 공식을 적용한다.
STEP1. 결합분포의 로그 - 이차식 형태
정규화 상수를 제외하고 결합분포 $p(\mathbf{z}, \mathbf{y})$에 로그를 취하면 다음과 같다.
$$\log p(\mathbf{z}, \mathbf{y}) = -\frac{1}{2} (\mathbf{z} - \mu_{z})^{T} \Sigma^{-1}_{z} (\mathbf{z} - \mu_{z}) - \frac{1}{2} (\mathbf{y} - \mathbf{W}\mathbf{z} - \mathbf{b})^{T}\Sigma^{-1}_{y}(\mathbf{y} - \mathbf{W}\mathbf{z} - \mathbf{b})$$
이 식은 $(\mathbf{z}, \mathbf{y})$에 대한 이차식이므로 결합분포는 가우시안이다.
STEP2. 이차식 전개 → 정밀도(Precision) 행렬 정의
$$\begin{align} Q &= -\frac{1}{2} \mathbf{z}^{T}\Sigma^{-1}_{z}\mathbf{z} - \frac{1}{2}\mathbf{y}^{T}\Sigma^{-1}_{y}\mathbf{y} - \frac{1}{2} (\mathbf{W}\mathbf{z})^{T}\Sigma^{-1}_{y}(\mathbf{W}\mathbf{z}) + \mathbf{y}^{T}\Sigma^{-1}_{y}\mathbf{W}\mathbf{z} \\ &= -\frac{1}{2} \begin{pmatrix} \mathbf{z} \\ \mathbf{y} \end{pmatrix}^{T} \begin{pmatrix} \Sigma_{z}^{-1} + \mathbf{W}^{T}\Sigma_{y}^{-1}\mathbf{W} & -\mathbf{W}^{T}\Sigma_{y}^{-1} \\ -\Sigma_{y}^{-1}\mathbf{W} & \Sigma^{-1}_{y} \end{pmatrix} \begin{pmatrix} \mathbf{z} \\ \mathbf{y} \end{pmatrix} \\ &= -\frac{1}{2}\begin{pmatrix} \mathbf{z} \\ \mathbf{y} \end{pmatrix}^{T} \Sigma^{-1} \begin{pmatrix} \mathbf{z} \\ \mathbf{y} \end{pmatrix} \end{align}$$
여기서 정밀도 행렬 $\Lambda$을 다음과 같이 정의한다.
$$\Sigma^{-1} = \begin{pmatrix} \Sigma^{-1}_{z} + \mathbf{W}^{T}\Sigma_{y}^{-1}\mathbf{W} & -\mathbf{W}^{T}\Sigma_{y}^{-1} \\ -\Sigma_{y}^{-1}\mathbf{W} & \Sigma^{-1}_{y} \end{pmatrix} = \begin{pmatrix} \Lambda_{zz} & \Lambda_{zy} \\ \Lambda_{yz} & \Lambda_{yy} \end{pmatrix} = \Lambda$$
STEP3. 가우시안 조건화 공식 적용
먼저 사후 공분산 $\Sigma_{z|y}$와 사후 평균 $\mu_{z|y}$를 가우시안 조건화 공식을 이용해서 다음과 같이 구할 수 있다.
$$\Sigma_{z|y} = \Lambda^{-1}_{zz} = (\Sigma_{z}^{-1} + \mathbf{W}^{T}\Sigma_{y}^{-1}\mathbf{W})$$
$$\begin{align} \mu_{z|y} &= \Sigma_{z|y} (\Lambda_{zz}\mu_{z} - \Lambda_{zy}(\mathbf{y} - \mu_{y})) \\ &= \Sigma_{z|y} (\Sigma^{-1}_{z}\mu_{z} + \mathbf{W}^{T}\Sigma^{-1}_{y}\mathbf{W}\mu_{z} + \mathbf{W}^{T}\Sigma^{-1}_{y}(\mathbf{y} - \mu_{y})) \\ &= \Sigma_{z|y} (\Sigma^{-1}_{z}\mu_{z} + \mathbf{W}^{T}\Sigma^{-1}_{y}(\mathbf{W}\mu_{z} + \mathbf{y} - \mu_{y})) \\ &= \Sigma_{z|y} (\Sigma^{-1}_{z}\mu_{z} + \mathbf{W}^{T}\Sigma^{-1}_{y}(\mathbf{y} - \mathbf{b})) \end{align}$$
이제 간단한 예시로 선형 가우시안 시스템을 이해해보도록 하겠습니다. 핵심은 "측정이 많아질수록 얼마나 빨리 불확실성이 줄어드는 가, 그리고 사전확률분포과 데이터가 어떻게 타협하는가?"를 수식으로 직접 확인하려고 합니다. 일단, 문제 설정을 하도록 하겠습니다. $z$를 알고싶은 미지의 스칼라라고 가정하고 $y_{i}$를 총 $N$개의 잡음이 포함된 측정치라고 하겠습니다. 즉, $p(y_{i}|z) = \mathcal{N}(y_{i}|z, \lambda_{y}^{-1})$이죠. 쉽게 생각하자면 관측값 $y_{i}$는 참값 $z$ 주위에 분산 $\sigma^{2}$을 갖는 가우시안 노이즈를 더한 형태로 보시면 됩니다. 여기서, $\lambda_{y} = \frac{1}{\sigma^{2}}$은 측정 정밀도로 이전에 말씀드렸듯이 분산의 역수로 정의됩니다. 마지막으로 $p(z) = \mathcal{N}(z | \mu_{0}, \lambda_{0}^{-1})$을 $z$에 대한 사전확률분포라고 가정하겠습니다.
문제의 목표에 따르면 저희는 $p(z|y_{1}, \dots, y_{N}, \sigma^{2})$을 계산하고 싶습니다. 이제 저희는 지금까지 배운 가우시안에 대한 베이즈 룰을 적용해서 표현해보도록 하겠스빈다. 이를 위해 다수의 관측치를 벡터로 묶어 $\mathbf{y} = (y_{1}, \dots, y_{N})$이라고 하고 $\mathbf{W} = \mathbf{1}_{N}$, 즉 $N \times 1$의 1로 채워진 벡터라고 정의하겠습니다. 마지막으로 $\Sigma^{-1}_{y} = \text{diag}(\lambda_{y}\mathbf{I})$라고 정의하겠습니다. 그러면 다음과 같이 $p(z|y_{1}, \dots, y_{N}, \sigma^{2})$에 대해 베이즈 룰을 적용할 수 있습니다.
$$\begin{cases} p(z | \mathbf{y}) &= \mathcal{N}(z | \mu_{N}, \lambda_{N}^{-1}) \\ \lambda_{N} = \lambda_{0} + N\lambda_{y} \\ \mu_{N} &= \frac{N\lambda_{y}\bar{y} + \lambda_{0}\mu_{0}}{\lambda_{N}} = \frac{N\lambda_{y}}{N\lambda_{y} + \lambda_{0}} \bar{y} + \frac{y_{0}}{N\lambda_{y} + \lambda_{0}}\mu_{0} \end{cases}$$
여기서 $\bar{y} = \frac{1}{N}\sum_{i = 1}^{N} y_{i}$로 관측값의 평균입니다. 이 결과를 해석해보도록 하죠.
- 정밀도는 사전 정밀도 + 측정 정밀도 $\times$ 측정 데이터 개수로 단순하게 얻을 수 있습니다.
- 평균은 사전 평균 $\mu_{0}$와 최우추정치(MLE)인 표본평균 $\bar{y}$의 가중 평균으로 얻습니다.
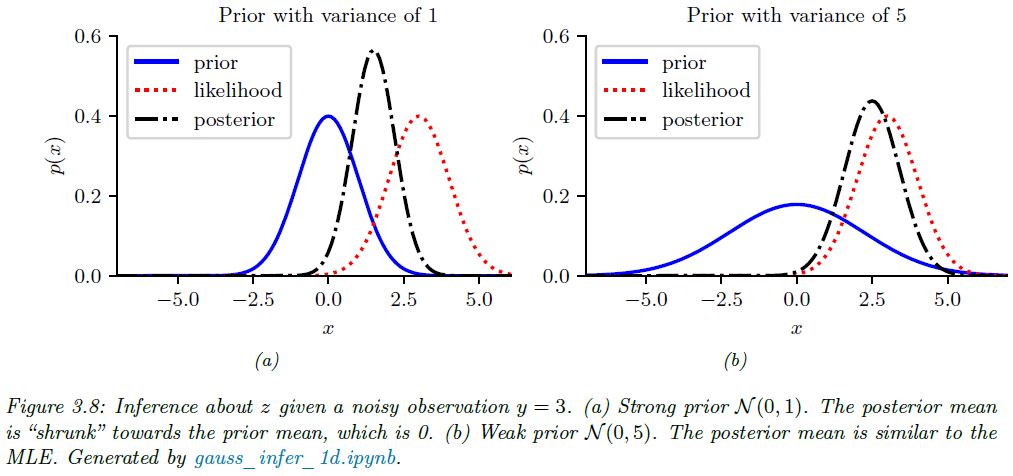
이 결과를 보면 그림 3.8과 같이 사전확률이 약하면 ($\lambda_{0} < N\lambda_{y}$) 데이터 쪽으로 반대로 사전이 강하면 그 반대로 더 기울게 됩니다.
지금까지 저희는 정밀도를 기준으로 확인했으니 이번에는 역으로 분산을 기준으로 분석해보도록 하겠습니다. 그러면 다음과 같이 쓸 수 있죠.
$$\begin{cases} p(z| \mathcal{D}, \sigma^{2}) &= \mathcal{N}(z | \mu_{N}, \tau_{N}^{2}) \\ \tau_{N}^{2} &= \frac{1}{\frac{N}{\sigma^{2}} + \frac{1}{\tau_{0}^{2}}} = \frac{\sigma^{2}\tau_{0}^{2}}{N\tau_{0}^{2} + \sigma^{2}} \\ \mu_{N} &= \tau_{N}^{2} \left( \frac{\mu_{0}}{\tau^{2}_{0}} + \frac{N\bar{y}}{\sigma^{2}} \right) = \frac{\sigma^{2}}{N\tau_{0}^{2} + \sigma^{2}} \mu_{0} + \frac{N\tau_{0}^{2}}{N\tau_{0}^{2} + \sigma^{2}}\bar{y} \end{cases}$$
여기서 $\tau_{0}^{2} = \frac{1}{\lambda_{0}}$와 $\tau_{N}^{2} = \frac{1}{\lambda_{N}}$은 각각 사전 분산과 사후 분산을 의미합니다. 이 수식은 처음에 정밀도를 기준으로 했을 때와 굉장히 달라보이지만 그 해석은 동일합니다.
저희는 총 $N$개의 데이터를 한번에 관측했다고 가정했습니다. 그렇다면 한 개씩 관측하는 경우에는 어떨까요? 즉, $N = 1$이라고 가정하겠습니다. 먼저 1개의 관측 $y$를 본 뒤 사후는 다음과 같이 계산할 수 있습니다.
$$\begin{cases} p(z | y) &= \mathcal{N}(z|\mu_{1}, \Sigma_{1}) \\ \Sigma_{1} &= \left( \frac{1}{\Sigma_{0}} + \frac{1}{\Sigma_{y}} \right)^{-1} = \frac{\Sigma_{y}\Sigma_{0}}{\Sigma_{0} + \Sigma_{y}} \\ \mu_{1} &= \Sigma_{1} \left( \frac{\mu_{0}}{\Sigma_{0}} + \frac{y}{\Sigma_{y}} \right)\end{\cases}$$
여기서 $\Sigma_{1} = \sigma^{2}$ 이고 $\Sigma_{0} = \tau_{0}^{2}$입니다. 여기서 $\mu_{1}$을 총 3가지 관점에서 다르게 볼 수 있습니다.
$$\begin{align} \mu_{1} &= \frac{\Sigma_{y}}{\Sigma_{y} + \Sigma_{0}}\mu_{0} + \frac{\Sigma_{0}}{\Sigma_{y} + \Sigma_{0}}y \\ &= \mu_{0} + (y - \mu_{0})\frac{\Sigma_{0}}{\Sigma_{y} + \Sigma_{0}} \\ &= y - (y - \mu_{0}) \frac{\Sigma_{y}}{\Sigma_{y} + \Sigma_{0}} \end{align}$$
이때 첫번째 식은 사전확률과 데이터의 볼록 조합(Convex Combination)으로 볼 수 있습니다. 그리고 두번째 식은 사전 데이터가 관측된 데이터쪽으로 이동한 것으로 볼 수 있으며, 세번째 식은 데이터를 사전 데이터쪽으로 수축(Shrinkage)했다고 볼 수 있죠. 이때, 신호-대-잡음비 (Signal-to-Noise Ratio; SNR)라고 불리는 수축정도를 양적으로 표현할 수 있는 방법이 있습니다.
$$\text{SNR} = \frac{\mathbb{E}[Z^{2}]}{\mathbb{E}[\epsilon^{2}]} = \frac{\Sigma_{0} + \mu_{0}^{2}}{\Sigma_{y}}$$
여기서 $z \sim \mathcal{N}(\mu_{0}, \Sigma_{0})$은 실제 신호를 의미하고 $y = z + \epsilon$은 관측된 신호로 $\epsilon \sim \mathcal{N}(0, \Sigma_{y})$로 잡음 항(Noise Term)입니다.
