1. 정의(Definition)
지금까지 저희는 가우시안 분포 또는 베르누이 분포 등 단일 분포를 중심으로 알아보았습니다. 하지만 현실 세계에서는 다양한 복잡한 분포들이 더 존재할 수 있습니다. 이를 위해 사용할 수 있는 방법이 바로 혼합 모델(Mixture Model) 입니다. 즉, 간단한 분포들을 볼록 결합(Convex Combination)을 통해 사용하는 것이죠. 수식적으로는 다음과 같이 정의됩니다.
$$p(\mathbf{y} \mid \mathbf{\theta}) = \sum_{k = 1}^{K} \pi_{k} p_{k}(\mathbf{y})$$
여기서 $p_{k}(\mathbf{y})$는 $k$번째 혼합 성분(Mixture Component)으로 확률 분포라고 생각하시면 됩니다. 그리고 $\pi_{k}$는 혼합 가중치(Mixture Coefficient)로 $k$번째 혼합 성분 $p_{k}(\mathbf{y})$를 새로운 혼합 모델에 얼마나 영향을 끼칠지를 결정하는 요소입니다. 이 혼합 가중치는 $0 \le \pi_{k} \le 1$ 그리고 $\sum_{k = 1}^{K} \pi_{k} = 1$ 조건을 항상 만족합니다.
이 혼합 모델을 새롭게 표현해볼 수도 있습니다. 이를 계층적 표현(Hierarchical Representation)이라고 하죠. 핵심적인 아이디어는 "어떤 혼합 성분을 사용할 지"를 알려주는 잠재 변수(latent variable) $z \in \{ 1, \dots, K \}$을 도입하는 것 입니다.
$$\begin{cases} p(z\mid \mathbf{\theta}) &= \text{Cat} (z \mid \mathbf{\pi}) \\ p(\mathbf{y} \mid z = k, \mathbf{\theta}) &= p(\mathbf{y} \mid \mathbf{\theta}_{k}) \end{cases}$$
여기서 $\theta = (\pi_{1}, \dots, \pi_{K}, \theta_{1}, \dots, \theta_{K})$로 모델 파라미터로 정의됩니다. 전체적인 수식을 해석해보도록 하겠습니다. 일단, 카테고리 분포 $\text{Cat}(z \mid \mathbf{\pi})$에서 $z$를 뽑아 혼합 성분을 결정합니다. 그리고 선택된 성분 $k$의 파라미터 $\theta_{k}$로부터 관측값 $\mathbf{y}$를 생성하는 것이죠. 결국 중간 잠재변수 $z$가 중간 다리 역할을 하는 것이라고 볼 수 있습니다.
그렇다면 이렇게 계층적인 표현을 했을 때 원래 식으로 만들수도 있지 않을까요? 여기서 저희가 이전에 배웠던 주변화(Marginalization)을 수행하면 됩니다. 이때 $z$는 처음에 이산형 변수라고 가정했기 때문에 가능한 $z \in \{ 1, \dots, K \}$에 대한 모든 합을 취해주면 다음과 같이 식을 전개할 수 있습니다.
$$\begin{align} p(\mathbf{y} \mid \mathbf{\theta}) &= \sum_{k = 1}^{K} p(z = k \mid \mathbf{\theta})p(\mathbf{y} \mid z = k, \mathbf{\theta}) \\ &= \sum_{k = 1}^{K} \pi_{k}p(\mathbf{y} \mid \mathbf{\theta}) \end{align}$$
저희는 이제 혼합성분을 어떤식으로 정의하느냐에 따라 굉장히 다양한 종류의 혼합 모델을 만들 수 있습니다. 예를 들어, 정규 분포를 사용하면 가우시안 혼합 모델(Gaussian Mixture Model; GMM) 그리고 베르누이 분포를 쓰면 베르누이 혼합 모델(Bernoulli Mixture Models; BMM), 또한 서로 다른 형태의 분포들을 섞어서 쓰면 멀티모달 데이터도 설명할 수 있죠. 결국 혼합 모델은 **“어떤 단일 분포로는 설명하기 어려운 데이터”**를 효과적으로 표현할 수 있는 강력한 도구입니다. 위와 같이 잠재 변수를 도입해 위계적으로 해석하면, 학습(EM 알고리즘 등)과 추론(베이지안 방법) 모두 직관적으로 이해하고 구현할 수 있습니다.
2. 혼합 모델의 예시(Examples)
2.1 가우시안 혼합 모델(Gaussian Mixture Model; GMM)
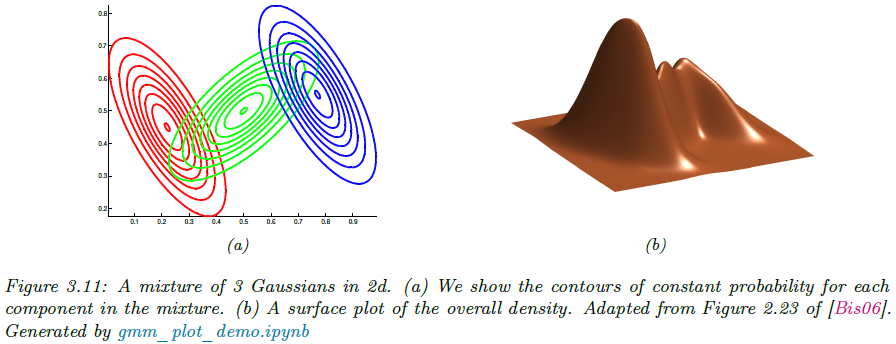
가우시안 혼합 모델, 줄여서 GMM(또는 Mixture of Gaussian; MoG)는 여러 개의 가우시안 분포를 가중합한 확률 모델로 다음과 같이 정의됩니다. 그림 3.11은 그 예시를 보여주고 있습니다.
$$p(\mathbf{y} \mid \mathbf{\theta}) = \sum_{k = 1}^{K} \pi_{k} \mathcal{N}(\mathbf{y} \mid \mu_{k}, \Sigma_{k})$$
여기서 기존의 혼합모델의 혼합 성분 $ p_{k}(\mathbf{y}) $가 단순히 가우시안 분포로 정의되기만 하면 됩니다. GMM이 가장 활발하게 사용되는 분야는 비지도 군집화(Unsupervised Clustering)일 것 입니다. 실수형 벡터 $\mathbf{y} \in \mathbb{R}^{D}$가 있다고 가정하겠습니다. 이를 위해 먼저 MLE를 통해 파라미터를 추정합니다.
$$\hat{\mathbf{\theta}} = \text{argmax}_{\mathbf{\theta}} \log(p(\mathcal{D} \mid \mathbf{\theta}))$$
이때 자세한 학습 방식은 향후이 설명드리도록 하겠습니다. 다음 단계는 각 데이터 $y_{n}$이 어떤 성분에서 왔는지를 나타내는 숨은 변수인 잠재성분 $z_{n} \in \{ 1, 2, \dots, K \}$에 대한 사후확률을 계산해야합니다.
$$r_{nk} = p(z_{n} \mid \mathbf{y}_{n}, \mathbf{\theta}) = \frac{p(z_{n} = k \mid \mathbf{\theta})p(\mathbf{y}_{n} \mid z_{n} = k, \mathbf{\theta})}{\sum_{k^{'} = 1}^{K} p(z_{n} = k^{'} \mid \mathbf{\theta})p(\mathbf{y}_{n} \mid z_{n} = k^{'}, \mathbf{\theta})}$$
여기서 $r_{nk}$는 군집 $k$에 대한 책임도(reponsibility)라고 불리며 데이터 $n$을 설명할 때 가우시안 분포 $k$이 설명한 책임 비율입니다.

그림 3.12와 같이 마지막 단계로 군집화를 수행할 때 하드 군집화(Hard Clustering)과 소프트 군집화(Soft Clustering) 중 하나를 선택할 수 있습니다. 하드 군집화를 하게 되면 가장 가능성이 높은 한 클러스만 선택하게 되고 소프트 군집화를 수행하면 책임도 $r_{nk}$를 가중치로 삼아서 여러 클러스터링에 분할하고 배정합니다.
2.2 베르누이 혼합 모델(Bernoulli Mixture Models; BMM)
관측된 데이터가 이진 데이터라면 가우시안 분포대신 베르누이 혼합 모델, 줄여서 BMM( 또는 Mixture of Bernoulli; MoB)를 사용할 수 있습니다. 일단 베르누이 분포를 아래와 같이 정의됩니다.
$$p(\mathbf{y} \mid z = k, \mathbf{\theta}) = \prod_{d = 1}^{D} \text{Ber}(y_{d} \mid \mu_{dk}) = \prod_{d = 1}^{D} \mu_{dk}^{y_{d}}(1 - \mu_{dk})^{1 - y_{d}}$$
여기서 $y_{d} \in \{0, 1\}$은 $d$번째 비트이고 $\mu_{dk}$는 군집 $k$에서 비트 $d$가 1이 될 확률을 의미합니다. 전체모델을 혼합가중치 $\pi_{k}$를 이용해서 다음과 같이 정의하게 됩니다.
$$p(\mathbf{y} \mid \mathbf{\theta}) = \sum_{k = 1}^{K} \pi_{k} p(\mathbf{y} \mid z = k, \mathbf{\theta})$$

그림 3.13은 BMM을 통해 MNIST로 학습하여 얻은 군집화 결과와 가중치 $\pi_{k}$를 보여주고 있습니다. 시각화 결과를 보면 ‘0’ ~ ‘9’ 각 숫자 모양이 여러 버전으로 나타나는데, 이는 모델이 숫자 종류를 자동으로 “발견”했음을 보여줍니다. 베르누이 혼합 모델은 바이너리 피처(텍스트의 단어 출현, 흑백 이미지의 픽셀 등)에 자연스럽게 맞춰져 있습니다. GMM처럼 책임도–EM 구조를 그대로 활용하면서, 확률적 픽셀 패턴까지 학습해 “어떤 모양이 어떤 클러스터에 속하는가”를 명확히 파악할 수 있다는 장점이 있습니다.
