1. 정의(Definition)
I basically know of two principles for treating complicated systems in simple ways: the first is the principle of modularity and the second is the principle of abstraction. I am an apologist for computational probability in machine learning because I believe that probability theory implements these two principles in deep and intriguing ways — namely through factorization and through averaging. Exploiting these two mechanisms as fully as possible seems to me to be the way forward in machine learning. — Michael Jordan, 1997
확률론 및 컴퓨터공학의 대가 마이클 조던(Michael I. Jordan) 교수는 확률 모델에 대해 위와 같이 설명하였습니다. 결론적으로 확률 모델은 ‘분해(모듈화)’로 복잡한 문제를 작은 조건부/주변 분포의 곱으로 나누고, ‘평균화(추상화)’로 불필요한 세부를 통합해 단순화하는 것입니다. 그리고 이를 그래프로 표현하면 조건부 독립 구조가 드러나 계산과 설계가 쉬워져 머신러닝에서 큰 힘을 발휘하게 된다는 것이죠.
이 모듈화-추상화 접근법은 훨씬 더 많은 랜덤 변수 집합에 대해서도 확장될 수 있습니다. 단, 한가지 중요한 가정을 두어야합니다. 어떤 변수들은 다른 변수들과 조건부로 독립(Conditional Independence; CI)이라는 점이죠. 이 CI 가정을 그래프(Graph)로 표현하면 복잡한 확률 모델을 훨씬 직관적으로 다룰 수 있죠. 실제로 이러한 그래프 표현 방식은 최근 딥 러닝 계열의 생성모델, 대표적으로 VAE, GAN, Diffusion Model 등에서 아직도 적극적으로 활용되고 있습니다. 오늘은 이 개념을 정말 간략하게 배워보도록 하겠습니다.
확률 그래프 모델(Probabilistic Graphical Model; PGM)은 여러 개의 확률 변수들 공유하는 공동 확률분포를 그래프로 표현하여 조건부 독립성 가정을 명시하는 기법입니다. 그래프가 유향 비순환 그래프(Directed Acyclic Graph; DAG)인 경우 이를 베이지안 네트워크(Bayesian network)라고 부르기는 하지만 이 모델이 반드시 베이지안적이지는 않습니다. 결국, 그래프로 표현해야하니 노드, 간선이 정의되어야겠죠. PGM에서 노드는 확률 변수, 그리고 간선은 직접적인 의존관계를 의미합니다. 따라서, 노드 간의 간선이 없는 경우에는 CI를 만족하게 되는 것이죠.
DAG에서는 노드를 위상 정렬(Topological Order), 즉 부모에서 자식 순으로 번호를 매길 수 있습니다. 이때, 각 노드는 부모집합 $\text{pa}(i)$만 알면 선행 노드 $\text{pred}(i)$ 중 부모가 아닌 나머지와 조건부로 독립니다. 이를 순서 마코프 성질(Ordered Markov Property)라고 하죠.
$$Y_{i} \perp Y_{\text{pred}(i) \text{pa}(i)} \mid Y_{\text{pa}(i)}$$
따라서, 전체 공동 분포는 다음과 같이 조건부 분포의 곱으로 표현할 수 있습니다.
$$p(\mathbf{Y}_{1:N_{G}}) = \prod_{i = 1}^{N_{G}} p(Y_{i}|\mathbf{Y}_{\text{pa}(i)})$$
여기서 $N_{G}$는 그래프의 노드(변수)의 개수를 의미합니다. 그런데 곱셈 항 하나하나는 작은 로컬 모델이므로 모델링에서 변수마다 필요한 부모 노드만 고르면 되므로 구조가 단순해지고 학습·추론 시 파라미터 추정이나 샘플링을 “블록별”로 병렬·분할 처리할 수 있어 계산이 빨라집니다. 결국 위 식은 “그래프 구조가 주는 독립성 가정 덕분에, 거대한 다변량 확률분포도 작고 단순한 조각들의 곱으로 표현‧학습‧추론할 수 있다”는 사실을 공식으로 요약한 것입니다.
2. 예시: 마르코프 체인(Markov Chain)
이를 활용한 가장 대표적인 확률 모델이 바로 마르코프 체인(Markov Chain)입니다. 가변 길이 시퀀스 $y_{1:T}$에 대한 공동 확률분포 $p(y_{1:T})$를 만들고 싶다고 가정하겠습니다. 각 원소 $y_{t}$가 $K$개의 값을 갖는 단어를 의미한다고 할 때 $y_{t} \in \{ 1, \dots, K \}$이고 모델은 길이 $T$인 문장의 분포를 나타냅니다. 이런 모델을 언어 모델(Language Model)이라고 부르죠. 한편, 확률의 곱셈 법칙에 따르면 $T$개의 변수의 어떠한 공동 확률분포도 다음과 같이 표현할 수 있습니다.
$$p(\mathbf{y}_{1:T}) = p(y_{1})p(y_{2} \mid y_{1})p(y_{3} \mid y_{2}, y_{1}) \cdots = \prod_{t = 1}^{T} p(y_{t} \mid \mathbf{y}_{1:t - 1})$$
하지만, 조건부 분포 $p(y_{t} \mid \mathbf{y}_{1:t - 1})$를 모두 담으려면 파라미터 수가 지수적으로 증가합니다. 이러한 문제를 해결하기 위해 1차 마르코프 조건(first‑order Markov condition)을 가정합니다. 즉, "현재 상태 $y_{t}$만 알면 미래 $\mathbf{y}_{t+1:T}$는 과거 $\mathbf{y}_{1:t-1}$와 독립이다"라는 것이죠. 이를 만족하는 PGM은 그림 3.15(a)과 같이 그릴 수 있으며 수식적으로도 표현할 수 있습니다.
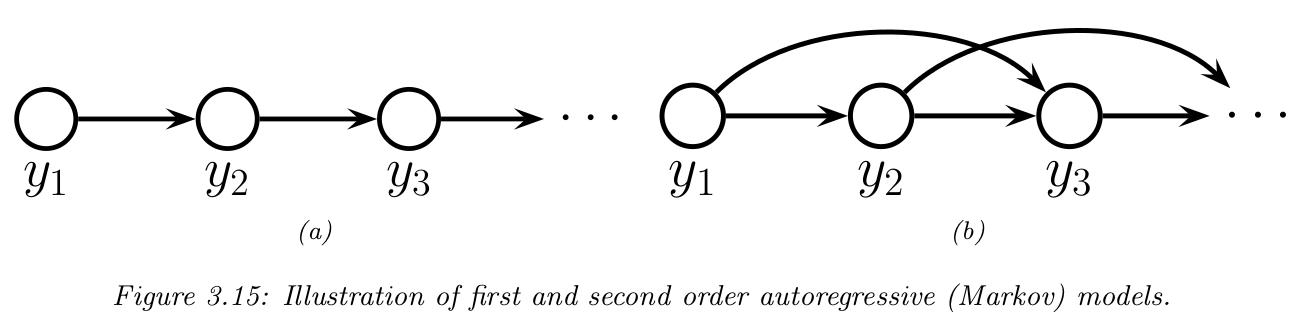
$$p(\mathbf{y}_{1:T}) = p(y_{1})p(y_{2} \mid y_{1})p(y_{3} \mid y_{2}) \cdots = \prod_{t = 1}^{T} p(y_{t} \mid y_{t - 1})$$
쉽게 말하면 현재상태는 바로 직전과거 상태에만 영향을 받는다는 의미입니다. 이러한 확률 모델을 마르코프 체인·마르코프 모델·1차 자기회귀(autoregressive) 모델이라 부릅니다. 이때, 각 조건부 분포 $P(y_{t} \mid y_{y - 1})$를 전이 함수(transition function), 전이 커널(transition kernel), 마르코프 커널이라고도 합니다. 이를 해석해보면 "지난 상태 $y_{t - 1}$가 $j$일 때 이번 상태 $y_{t}$가 $k$가 될 확률"라고 볼 수 있으며 $p(y_{t} \mid y_{t - 1}) \ge 0$이고 $\sum_{k = 1}^{K} p(y_{t} = k \mid y_{t - 1} = j) = 1$을 만족합니다. 이러한 조건부 확률표(Conditional Probabilistic Table; CPT)를 확률 행렬(Probabilistic Matrix) $A_{jk} = p(y_{t} = k \mid y_{t - 1} = j)$로 표현하며 각 행의 합이 1이 됩니다. 이때, 모든 시점에서 같은 확률행렬 $A$를 사용한다면 모델은 동질(homogeneous)·정상(stationary)·시간 불변(time‑invariant) 이라 합니다. 이는 여러 시점이 동일 파라미터를 공유(parameter tying) 한다는 뜻으로, 임의 길이의 시퀀스도 고정된 파라미터 수로 표현할 수 있게 해 줍니다.
하지만 굳이 바로 직전 상태만 고려해야할까요? 직전 상태만 고려하는 것은 실생활에서 꽤나 강력한 가정입니다. 따라서 이를 완화하기 위해 현재 상태가 마지막 $M$개의 관측치에 의존하게 만들면 됩니다.
$$p(\mathbf{y}_{1:T}) = p(\mathbf{y}_{1:M}) \prod_{t = M +1}^{T} p(y_{t} \mid \mathbf{y}_{t - M:t - 1})$$
이를 $M$차 마르코프 모델이라고 합니다. $M = 1$이라면 바이그램(bigram) 모델 그리고 $M = 2$이라면 트라이그램(trigram) 모델이라고 부릅니다. 이러한 구조는 그림 3.15(b)를 보시면 알 수 있습니다.
3. 추론(Inference)
PGM은 공동 확률분포를 기반으로 동작합니다. 따라서, 주변화와 조건부화 규칙을 이용해 임의의 변수 집합 $i$와 $j$에 대해 $p(\mathbf{Y}_{i} \mid \mathbf{Y}_{j} = \mathbf{y}_{j})$를 계산할 수 있습니다. 자세한 내용은 향후에 설명드리도록 하겠습니다. 다만, 이처럼 여러 원인이 같은 결과를 설명할 때, 한 원인을 관측하면 다른 원인의 필요성이 줄어드는 현상을 설명 상쇄 효과(explaining away effect) 또는 버크슨의 역설(Berkson’s paradox)이라 부릅니다.
4. 학습(Learning)
모형의 조건부 확률분포 파라미터가 알려져 있지 않다면, 이들 파라미터를 추가적인 확률 변수로 간주해 그래프에 노드로 추가한 뒤, 숨은(latent) 변수로서 추론할 수 있습니다.

그림 3.16(a)는 그 예시로 동일한 분포를 따르는 독립‧동일 분포(iid) 랜덤 변수 $\mathbf{y}_{n}$이 $N$개 있고 이들의 공통 파라미터가 $\theta$만 있는 상황을 보여주고 있습니다. 여기서 그늘진 노드는 관측값, 빈 노드는 잠재 변수나 파라미터를 뜻합니다. 보통 모델은 데이터를 다음 절차를 통해 생성했다고 가정합니다.
$$\begin{cases} \mathbf{\theta} &\sim p(\mathbf{\theta}) \\ \mathbf{y}_{n} &\sim p(\mathbf{y} \mid \mathbf{\theta}) \end{cases}$$
여기서 $p(\mathbf{\theta})$는 파라미터 $\mathbf{\theta}$에 대한 사전분포(prior distribution)아고 $p(\mathbf{y} \mid \mathbf{\theta})$는 관측값 $\mathbf{y}$의 우도 함수입니다. 따라서, 데이터 $\mathcal{D} = \{ \mathbf{y}_{1}, \dots, \mathbf{y}_{N} \}$와 파라미터 $\mathbf{\theta}$의 공동분포 $p(\mathcal{D}, \mathbf{\theta})$는 다음과 같습니다.
$$p(\mathcal{D}, \theta) = p(\mathbf{\theta}) p(\mathcal{D} \mid \mathbf{\theta})$$
이때 i.i.d 가정에 의해 우도는 $p(\mathcal{D}, \theta) = \prod_{n = 1}^{N} p(\mathbf{y}_{n} \mid \mathbf{\theta})$와 같이 샘플별 곱으로 분해됩니다. 여기서 데이터 벡터의 순서는 모델 정의에 중요하지 않습니다. 즉, PGM에서 말단 노드의 번호를 어떻게 재배열해도 모델은 그대로 입니다. 이런 성질을 교환가능성(exchangeability) 이라 부릅니다.
그림 3.16(a)에서 보면 $\mathbf{y}$가 $N$번 반복되어 그림이 복잡합니다. 이러한 시각적 혼란을 줄이기 위해 그림 3.16(b) 플레이트 표기법(Plate notation)을 사용하기도 합니다. 그냥 반복되는 변수들을 작은 상자로 둘러싸고 상자 오른쪽 아래에 반복 횟수를 적습니다. 이는 모델을 “펼칠(unroll)” 때, 상자 안 노드들이 그 숫자만큼 자동으로 복제된다고 약속합니다. 이 표기법은 특정 종류의 베이지안 모델을 간결하게 표현할 때 널리 사용됩니다.
