1 공분산(Covariance)
두 확률변수 $X$와 $Y$ 사이의 공분산은 두 변수가 서로 얼마나 선형적으로 관련되어 있는지를 나타내는 지표이며 다음과 같이 정의됩니다.
$$\text{Cov}[X, Y] = \mathbb{E}[(X - \mathbb{E}[X])(Y - \mathbb{E}[Y])] = \mathbb{E}[XY] - \mathbb{E}[X]\mathbb{E}[Y]$$
이때, 공분산 $\text{Cov}[X, Y]$이 양수라면 둘이 함께 증가(양의 상관성을 가짐)하게 되고 음수라면 한쪽이 증가할 때 다른 쪽은 감소(음의 상관성을 가짐)지며 0이라면 선형적인 상관관계가 없음을 의미합니다.
1.1 고차원 벡터의 공분산 행렬
$x$가 $D$차원 랜덤 벡터일 때 그 공분산 행렬은 다음과 같이 정의되며 대칭이고 양의 준정행렬(Posititve Semi-definite Matrix)입니다.
$$\begin{align} \text{Cov}[\mathbf{x}] &= \mathbb{E}[(\mathbf{x} - \mathbb{E}[\mathbf{x}])(\mathbf{x} - \mathbb{E}[\mathbf{x}])^{T}] \\ &= \Sigma = \begin{pmatrix} \mathbb{V}[X_{1}] & \text{Cov}[X_{1}, X_{2}] & \cdots & \text{Cov}[X_{1}, X_{D}] \\ \text{Cov}[X_{2}, X_{1}] & \mathbb{V}[X_{2}] & \cdots & \text{Cov}[X_{2}, X_{2}] \\ \vdots & \vdots & \ddots & \vdots \\ \text{Cov}[X_{D}, X_{1}] & \text{Cov}[X_{D}, X_{2}] & \cdots & \mathbb{V}[X_{D}] \end{pmatrix} \end{align}$$
이 행렬로부터 $\mathbb{E}[\mathbf{x}\mathbf{x}^{T}] = \Sigma + \mu\mu^{T}$임을 알 수 있습니다. 또한, 벡터 $\mathbf{x}$에 선형변환 $\mathbf{A}\mathbf{x} + \mathbf{b}$를 적용하면 새로운 공분산은 $\text{Cov}[\mathbf{A}\mathbf{x} + \mathbf{b}] = \mathbf{A}\text{Cov}[\mathbf{x}]\mathbf{A}^{T}$임을 알 수 있죠 (이에 대한 증명은 지난 포스팅 [PML intro] Ch2 Probability: Univariate Model (Sec2.8 Transformations of Random Variables)을 참고해주세요.).
1.2 교차 공분산(Cross‑Covariance)
서로 다른 두 랜덤벡터 $\mathbf{x}$와 $\mathbf{y}$ 사이의 교차 공분산은 다음과 같이 계산됩니다.
$$\text{Cov}[\mathbf{x}, \mathbf{y}] = \mathbb{E}[(\mathbf{x} - \mathbb{E}[\mathbf{x}])(\mathbf{y} - \mathbb{E}[\mathbf{y}])^{T}]$$
이는 $\mathbf{x}$의 각 성분과 $y$의 각 성분 사이의 상관관계를 행렬 형태로 나타낸것입니다.
2. 상관성(Correlation)
2.1 상관계수(Correlation Coefficient)
공분산의 값의 범위가 $-\infty$에서 $\infty$이기 때문에 크기를 직접적으로 비교하기 어렵습니다. 상관계수는 이를 $[-1, 1]$ 구간으로 정규화한 지표로 두 변수의 선형적 관계 정도를 나타냅니다.
$$\rho = \text{corr}[X, Y] = \frac{Cov[X, V]}{\mathbb{V}[X]\mathbb{V}[Y]}$$

그림 3.1에서 볼 수 있다싶이 여기서 $Y = aX + b$라고 할 때 $\rho = 1$이라면 $a > 0$안 완전한 양의 선형관계, $\rho = -1$이라면 완전한 음의 선형관계를 가지며 $\rho = 0$이라면 선형성이 없음을 의미합니다. 다만, 비선형 관계는 존재할 수도 있습니다. 이때, 회귀 직선 $Y = aX + b$의 기울기 $a = \frac{\text{Cov}[X, Y]}{\mathbb{V}[X]}$로 상관계수와는 별개입니다 (이 부분은 향후에 증명하도록 하겠습니다.). 상관계수는 기울기의 크기가 아니라 선형성의 정도를 측정합니다.
2.2 다변량 상관 행렬
관련 확률변수 벡터 $\mathbf{x} = (X_{1}, \dots, X_{D})^{T}$라고 할 때 상관행렬(Correlation Matrix)는 다음과 같이 정의됩니다.
$$\text{corr}[\mathbf{x}] = \begin{pmatrix} 1 & \frac{\mathbb{E}[(X_{1} - \mu_{1})(X_{2} - \mu_{2})]}{\sigma_{1}\sigma_{2}} & \cdots & \frac{\mathbb{E}[(X_{1} - \mu_{1})(X_{D} - \mu_{D})]}{\sigma_{1}\sigma_{D}} \\ \frac{\mathbb{E}[(X_{2} - \mu_{2})(X_{1} - \mu_{1})]}{\sigma_{2}\sigma_{1}} & 1 & \cdots & \frac{\mathbb{E}[(X_{2} - \mu_{2})(X_{D} - \mu_{D})]}{\sigma_{2}\sigma_{D}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\mathbb{E}[(X_{D} - \mu_{D})(X_{1} - \mu_{1})]}{\sigma_{D}\sigma_{1}} & \frac{\mathbb{E}[(X_{D} - \mu_{D})(X_{2} - \mu_{2})]}{\sigma_{D}\sigma_{2}} & \cdots & 1 \end{pmatrix}$$
여기서 $\mathbf{K}_{xx} = \Sigma = \mathbb{E}[(\mathbf{x} - \mathbb{E}[\mathbf{x}])(\mathbf{x} - \mathbb{E}[\mathbf{x}])^{T}] = \mathbf{R}_{xx} - \mu\mu^{T}$라고 정의하겠습니다. 이때, $\mathbf{K}_{xx}$는 자기 공분산 행렬(Auto-covariance Matrix)라고 부르며 $\mathbf{R}_{xx} = \mathbb{E}[\mathbf{x}\mathbf{x}^{T}]$는 자기 상관 행렬(Auto-correlation Matrix)라고 정의됩니다. 그러면 기존의 상관행렬은 다음과 같이 간단하게 표현됩니다.
$$\text{corr}[\mathbf{x}] = \left( \text{diag}(\mathbf{K}_{xx}) \right)^{-\frac{1}{2}} \mathbf{K}_{xx} \left( \text{diag}(\mathbf{K}_{xx}) \right)^{-\frac{1}{2}}$$
즉, 공분산 행렬을 각 변수의 표준편차로 양쪽에서 나눠 주면 상관 행렬이 됩니다.
3. 상관성에 대한 오해
3.1 상관이 없다고 해서 독립인 것은 아니다
두 확률변수 $X$와 $Y$가 독립이면 $p(X, Y) = p(X)p(Y)$가 성립합니다. 이 경우에는 $\text{Cov}[X, Y] = 0 \Rightarrow \text{corr}[X, Y] = 0$이므로 상관성이 없습니다. 하지만 그 역은 성립하지 않습니다. 즉, 상관계수가 0이라고 해서 두 변수가 독립은 아닙니다.
가장 대표적인 반례로 $X \sim U(-1, 1)$을 고려해보겠습니다. 즉, $X$를 $[-1, 1]$ 사이의 균등분포를 따르는 확률변수라고 가정하고 $Y = X^{2}$이라고 하겠습니다. 그러면 $Y$는 $X$에 의해 완전히 결정되므로 두 변수는 매우 강하게 의존하지만 실제로는 $\text{corr}[X, Y] = 0$입니다.
이러한 현상이 발생하는 이유는 상관계수는 오직 선형적 결합만을 측정하기 때문입니다. 보다 폭넓은 의존성을 정량화하려면 상호정보량(mutual information) 을 사용합니다. 상호정보량은 두 변수가 완전히 독립일 때만 0이 되므로, 선형·비선형 관계를 가리지 않고 의존성을 잡아낼 수 있습니다.
3.2 상관관계는 인과관계를 뜻하지 않는다
“상관관계(correlation)가 있다고 해서 인과관계(causation)가 있는 것은 아니다”라는 말은 통계·데이터 과학 분야의 대표적인 교훈입니다.

재미있는 예시를 통해 이를 알아보도록 하겠습니다. 그림 3.2에서 빨간선은 월별 아이스크림 판매량, 노란색은 같은 기간의 범죄율입니다. 두 시계열을 적절히 스케일링해 겹쳐 그리면 매우 높은 상관계수가 나타납니다. 실제로 “아이스크림을 많이 먹으면 살인이 늘어난다”는 식의 주장까지 있었습니다. 그러나 이는 허위(가짜) 상관관계로, 두 변수 모두 날씨(기온)라는 숨은 공통 원인에 영향을 받기 때문입니다.
무더운 날씨 → 사람들이 아이스크림을 더 많이 구매하게 되고 무더운 날씨 → (여러 가설)에 의해 더운 환경이 분노를 높여 폭력 사건 증가하거나 더 많은 인원이 야외 활동 → 범죄 노출 기회 증가될 수 있기 때문입니다. 즉, 아이스크림이 범죄를 유발한 것이 아니라, 둘 다 더운 날씨라는 제3의 요인에 의해 동시에 변화한 것입니다.
이처럼 예측 가능성($x$로 $y$를 잘 맞춘다)이 인과성($x$가 $y$를 일으킨다)을 보장하지 않습니다. 스푸리어스(spurious) 상관관계—숨은 공통 원인이나 우연에 의한 상관—를 경계해야 합니다. 보다 정확한 인과 추론을 위해서는 랜덤화 실험, 자연 실험, 구조적 인과 모델 등과 같은 추가적인 분석 기법을 필요로 합니다.
3.3 심슨의 역설 (Simpson’s paradox)
심슨의 역설은 여러 하위 집단에서 동일하게 나타나던 통계적 추세가, 집단을 모두 합쳐 분석할 때는 사라지거나 방향이 반대로 바뀌는 현상을 말합니다. 추세를 인과관계로 오해하면 매우 직관에 반하는 결론에 도달할 수 있으므로 주의가 필요합니다.

그림 3.3에서 전체 데이터를 보면 $x$가 커질수록 $y$는 감소합니다. 하지만 각 하위 집단(예: 색·마커로 구분)을 따로 보면, $x$가 커질수록 $y$는 증가하죠. 즉, 집단별로는 양(+)의 관계, 전체로는 음(−)의 관계가 동시에 존재합니다.
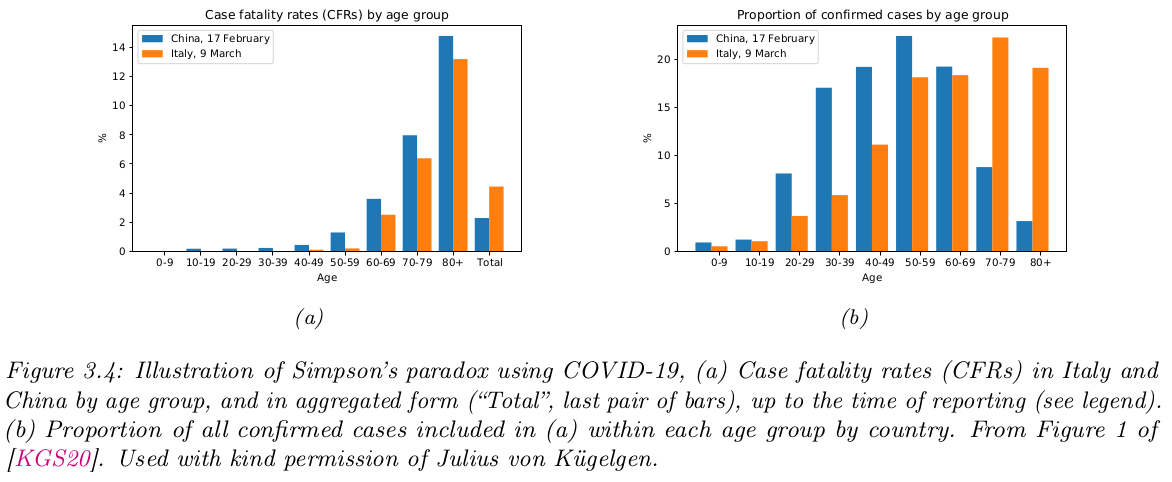
이번에는 다른 예시로 COVID19의 실제 사례를 보도록 하겠습니다. 그림 3.4.(a)를 보면 연령대별 $A$로 보면, 이탈리아의 COVID‑19 치명률(CFR)이 중국보다 낮습니다. 즉, $p(F = 1 | A, C = \text{Italy}) < p(F = 1 | A, C = \text{China})$. 여기서 $F = 1$은 "사망"을 의미합니다.
하지만, 그림 3.4.(b)를 보면 두 나라의 연령분포 $p(A|C)$가 다릅니다. 이탈리아는 고령 인구 비율이 더 높습니다. 연령분포를 가중 평균하면 오히려 $p(F = 1 | A, C = \text{Italy}) > p(F = 1 | A, C = \text{China})$가 되죠. 즉, 집단 내 비교와 집단 간 전체 비교가 정반대 결과를 보입니다.
이러한 현상이 발생하는 이유는 교란 변수(confounder)때문입니다. 하위 집단을 정의하는 변수(위 사례에서는 ‘연령’)가 주요 결과에도 영향을 미치면서, 나라별 비율이 크게 다르기 때문입니다. 집단을 합치면 교란 변수의 분포 차이가 섞여 본래의 추세를 뒤집어 버릴 수 있습니다.
정리하자면 심슨의 역설은 “부분에서 참, 전체에서 거짓” 또는 그 반대의 경우를 보여 줍니다. 통계적 의사결정·정책 수립·의료 연구 등에서 집단 구성 차이를 간과하면 잘못된 결론을 내릴 수 있으므로, 계층별 분석과 교란 변수 통제가 필수입니다.
