1 스튜던트 $t$-분포(Student's $t$-distribution)
일반적으로 많이 사용하는 가우시안 분표는 이상치(outlier)에 민감한 단점이 있습니다. 이에 비해 좀 더 이상치에 강건(robust)한 분포가 있는데, 그것이 바로 스튜던트 $t$-분포 (Student's $t$-distribution)입니다. 여기서는 간단히 "스튜던트 분포"라고 부르도록 하겠습니다. 스튜던트 분포의 PDF는 다음과 같은 형태로 표현됩니다.
$$\mathcal{T}(y|\mu,\sigma^{2},\nu) \propto \left[ 1 + \frac{1}{\nu} \left( \frac{y - \nu}{\sigma} \right)^{2} \right]^{-\frac{\nu + 1}{2}}$$
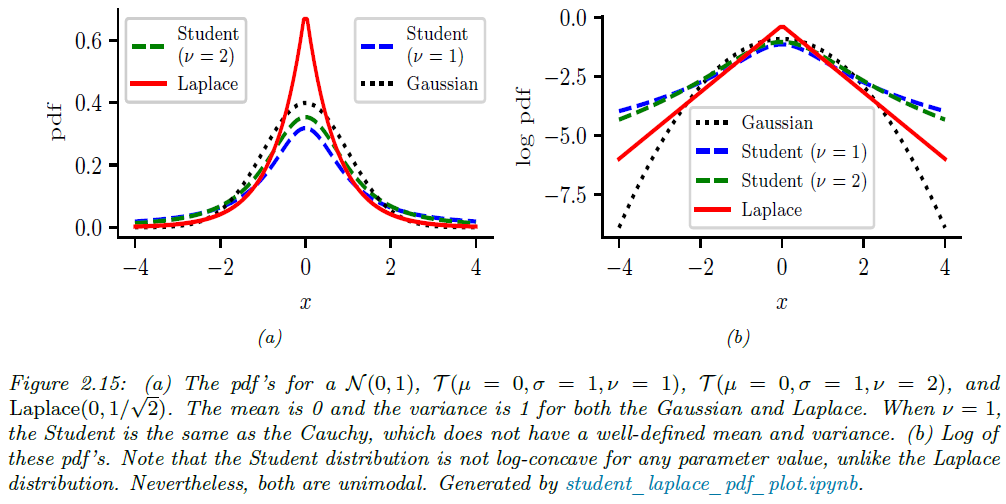
여기서 가우시안 분포와 유사하게 $\mu$는 평균을 나태나고 $\sigma > 0$은 분포의 폭을 결정하는 척도매개변수(scale parameter, 표준편차와 다른 개념), $\nu > 0$는 자유도(degrees of freedom)이라고 합니다. 사실 자유도보다는 "정규성의 정도(degree of normality)"라는 표현이 적합하기는 합니다. 왜냐하면 자유도 $\nu$값이 커질수록 스튜던트 분포의 모양이 가우시안 분포와 유사해지기 때문입니다 (그림 2.15).
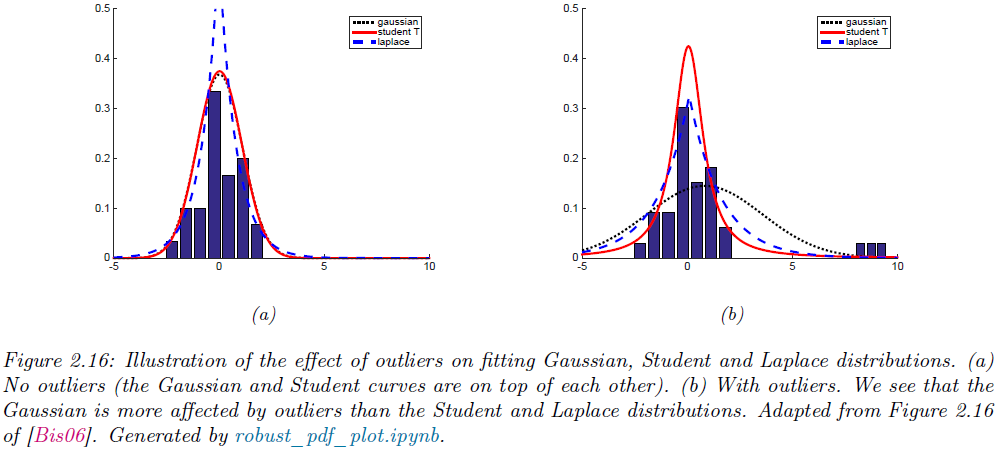
스튜던트 분포는 중심 $\mu$에서 멀어질수록 확률밀도가 제곱된 거리의 다항식 형태로 감소합니다. 이는 거리에 따라 지수적으로 감소하는 가우시안 분포보다 천천히 감소하는 것을 의미하며 이로 인해 꼬리부분에 더 많은 확률이 분포하게 됩니다 (그림 2.16). 이 현상을 "두꺼운 꼬리(heavy tails)"를 가진다라고 표현하며 이것이 스튜던트 분포가 이상치에 더 강건한 이유입니다.
스튜던트 분포의 강건성을 보다 명확하게 보여주는 예시를 살펴봅시다. 어떤 데이터에 이상치가 없을 때 가우시안 분포와 스튜던트 분포를 각각 피팅하면 비슷한 결과를 보입니다. 하지만 데이터에 이상치가 포함되었을 때는 가우시안 분포가 크게 영향을 받아 분포의 형태가 크게 변하는 반면, 스튜던트 분포는 거의 영향을 받지 않습니다. 이런 특성 덕분에 강건한 선형 회귀(robust linear regression) 모델에서 스튜던트 분포가 유용하게 사용됩니다.
추후의 참고를 위해 스튜던트 분포의 특성을 정리하면 평균은 $\mu$, 최빈값은 $\mu$, 그리고 분산은 $\frac{\nu\sigma^{2}}{\nu - 2}$입니다. 여기서 평균은 $\nu > 1$인 경우에만 존재하고 분산은 $\nu > 2$인 경우에만 정의됩니다. 만약 $1 \le \nu < 2$라면 스튜던트 분포의 분산은 $\infty$로 이야기합니다. 특히, $\nu$가 5이상으로 매우 커지면 스튜던트 분포는 빠르게 가우시안 분포에 근접하고 견고성의 장점도 잃어버리게 됩니다. 실제 어플리케이션에서는 $\nu = 4$ 정도로 선택하면 다양한 상황에서 좋은 성능을 보인다는 것이 알려져 있습니다.
2 코시 분포 (Cauchy Distribution)
스튜던트 분포에서 자유도 $\nu$가 1인 경우를 코시 분포(Cauchy Distribution) 또는 로렌츠 분포(Lorentz Distribution)라고 합니다. 코시 분포의 PDF는 다음과 같습니다.
$$\mathcal{C}(x|\mu, \gamma) = \frac{1}{\gamma \pi} \left[ 1 + \left( \frac{x - \mu}{\gamma} \right)^{2} \right]^{-1}$$
여기서 $\mu$는 분포의 중심, $\gamma > 0$는 분포의 폭을 나타내는 척도 매개변수입니다. 코시 분포는 정규분포(가우시안 분포)에 비해서 꼬리가 매우 두껍습니다. 이를 직관적으로 이해하기 위해 구체적인 예를 하나 들어보면 표준 정규분포에서 약 95%의 값은 -1.96에서 1.96 사이에 위치하지만 코시 분포는 같은 비율의 값이 무려 -12.7에서 12.7 사이에 존재할 만큼 넓게 분포합니다. 이 처럼 코시 분포의 꼬리는 굉장히 두꺼워서 평균값을 계산하기 위한 적분이 수렴하지 않습니다. 다시 말하자면, 코시 분포의 평균은 존재하지 않습니다.
2.1 반쪽 코시 분포 (Half Cauchy Distribution)
코시 분포에서 위치 매개변수 $\mu$를 0으로 고정한 뒤 음수 축 부분을 양수 축 쪽으로 접어서 만든 분포를 반쪽 코시 분포 (Half Cauchy Distribution)라고 합니다. 반쪽 코시 분포는 항상 양수 값만 가지며 다음과 같은 PDF를 가집니다.
$$\mathcal{C}_{+}(x|\gamma) = \frac{2}{\gamma \pi} \left[ 1 + \left( \frac{x}{\gamma} \right)^{2} \right]^{-1}$$
반쪽 코시 분포는 베이지안 모델링에서 유용하게 사용됩니다. 이는 양의 실수 영역에서 확률 분포를 지정할 때, 꼬리는 무겁고(heavy-tailed) 동시에 원점(0)에 유한한 확률밀도를 가지는 분포가 필요할 경우 유리하기 때문입니다.
3 라플라스 분포(Laplace Distribution)
또 다른 무거운 꼬리(heavy-tailed)를 가진 분포로 라플라스 분포(Laplace distribution)가 있습니다. 라플라스 분포는 양쪽 지수 분포(double-sided exponential distribution)라고도 불리며, 다음과 같은 PDF를 갖습니다.
$$\text{Laplace}(y|\mu, b) = \frac{1}{2b} \text{exp}\left( -\frac{|y - \mu|}{b} \right)$$
여기서 $\mu$는 분포의 중심, $b > 0$은 분포의 퍼짐을 나타냅니다. 그리고 평균은 $\mu$, 최빈값은 $\mu$ 그리고 분산은 $2b^{2}$으로 계산됩니다.
라플라스 분포는 중심에서 멀어질수록 지수적으로 감소하는 형태이지만, 정규 분포에 비해서는 꼬리가 더 무겁습니다. 이런 특성 덕분에 이상치(outlier)에 대해 더 강건한(robust) 특성을 보입니다. 향후 라플라스 분포를 이용한 견고한 선형회귀(robust linear regression) 방법과 희소 선형회귀(sparse linear regression) 방법에 대해서 더 알아보도록 하겠습니다.
4 베타 분포(Beta Distribution)
베타 분포(Beta Distribution)는 확률변수가 항상 $[0, 1]$ 사이의 값만 갖는 분포로 PDF는 다음과 같이 정의됩니다.
$$\text{Beta}(x|a,b) = \frac{1}{B(a, b)}x^{a - 1}(1 - x)^{b - 1}$$
여기서 $a, b$는 베타 분포의 모양을 결정하는 매개변수로 둘 다 양수여야합니다. 그리고 $B(a, b) = \frac{\Gamma(a)\Gamma(b)}{\Gamma(a + b)}$로 베타함수로 정의되며 이때 $\Gamma(a) = \int_{0}^{\infty} x^{a - 1}e^{-x} \; dx$는 감마함수입니다.
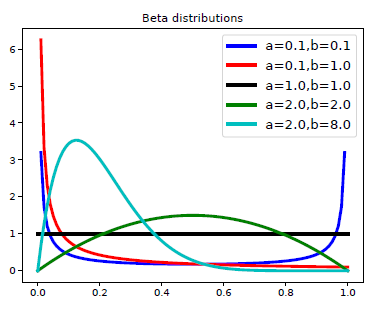
베타 분포는 $a$와 $b$의 값에 따라 다른 현상을 보이기 때문에 대표적인 특성만 알아보도록 하겠습니다.
- $a = b = 1$이라면 베타분포는 $[0, 1]$구간에서 균일 분포(Uniform Distribution)이 됩니다.
- $a < 1$이고 $b < 1$이라면 0과 1 양 끝부분에서 밀도가 높아지는 쌍봉 분포(Bimodal Distribution)가 됩니다.
- $a > 1$이고 $b > 1$이라면 하나의 봉우리를 가지는 단봉 분포(Unimodal Distribution)가 됩니다.
이때 베타 분포의 평균은 $\frac{a}{a + b}$, 최빈값은 $\frac{a - 1}{a + b - 2}$ 그리고 분산은 $\frac{ab}{(a + b)^{2}(a + b + 1)}$로 계산되며 최빈값의 경우에는 $a > 1$이고 $b > 1$인 경우에 유효합니다. 만약 $a < 1$이고 $b \ge 1$이라면 최빈값은 0이고 $a \ge 1$이고 $b < 1$이라면 최빈값은 1입니다.
5 감마 분포(Gamma Distribution)
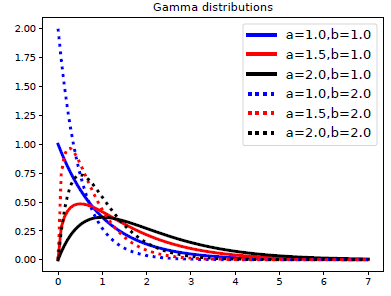
감마 분포(Gamma Distribution) 는 양의 실수값 $x > 0$을 가지는 확률변수를 위한 매우 유연한 분포입니다. 두 가지 매개변수로 정의되며, 각각 모양 매개변수 $a > 0$ 그리고 비율 매개변수 $b > 0$으로 나타내며 다음과 같은 PDF를 갖습니다.
$$\text{Ga}(x|\text{shape} = a, \text{rate} = b) = \frac{b^{a}}{\Gamma(a)} x^{a - 1}e^{-xb}$$
때때로 비율 매개변수 $b$의 역수인 척도 매개변수 $s = \frac{1}{b}$를 사용하여 다음과 같이 PDF를 표현하기도 합니다.
$$\text{Ga}(x|\text{shape} = a, \text{scale} = s) = \frac{1}{s^{a}\Gamma(a)} x^{a - 1}e^{-\frac{x}{s}}$$
이때, 감마분포의 평균은 $\frac{a}{b}$, 최빈값은 $\text{max}\left( \frac{a - 1}{b}, 0 \right)$, 그리고 분산은 $\frac{a}{b^{2}}$으로 계산됩니다. 감마분포는 굉장히 유연하게 변할 수 있는 분포로 다음과 같은 몇 가지 특별한 분포의 일반적 형태로 활용됩니다.
5.1 지수 분포(Exponential Distribution)
감마 분포에서 모양 매개변수를 1로 설정한 특별한 경우입니다.
$$\text{Expon}(x|\lambda) = \text{Ga}(x|\text{shape} = 1, \text{rate} = \lambda)$$
이 분포는 포아송 과정(Poisson process)에서 사건(event) 사이의 시간 간격을 모델링할 때 자주 사용됩니다. 포아송 과정은 사건들이 일정한 평균 발생률 $\lambda$로 연속적이고 독립적으로 일어나는 확률과정입니다.
5.2 카이제곱 분포(Chi-Squared($\chi^{2}$) Distribution)
감마 분포에서 모양 매개변수를 $\nu^{2}$, 비율 매개변수를 $\frac{1}{2}$로 설정한 경우를 카이제곱 분포(Chi-Squared($\chi^{2}$) Distribution)라고 합니다.
$$\chi^{2}_{\nu}(x) = \text{Ga}(x|\text{shape} = \frac{\nu}{2}, \text{rate} = \frac{1}{2})$$
여기서 $\nu$는 자유도(degrees of freedom)를 나타냅니다. 카이제곱 분포는 독립적인 표준정규분포 $Z_{i} \sim \mathcal{N}(0, 1)$를 제곱하여 합산한 값의 분포입니다. 정확히 말하면 $Z_{i} \sim \mathcal{N}(0, 1)$이고 $S = \sum_{ i = 1}^{\nu} Z_{i}^{2}$라면 $S \sim \chi^{2}_{\nu}$입니다.
5.3 역감마 분포(Inverse Gamma Distribution)
역감마 분포(Inverse Gamma distribution)는 다음과 같이 정의됩니다:
$$\text{IG}(x|\text{shape} = a, \text{scale} = b) = \frac{b^{a}}{\Gamma(a)}x^{-(a + 1)}e^{-\frac{b}{x}}$$
역감마 분포의 평균은 $\frac{b}{a - 1}$, 최빈값은 $\frac{b}{a + 1}$ 그리고 분산은 $\frac{b^{2}}{(a - 1)^{2}(a - 2)}$로 계산되며 평균의 경우 $a > 1$일 때, 분산의 경우 $a > 2$일 때 계산가능합니다.
여기서 만약 $X \sim \text{Ga}(\text{shape} = a, \text{rate} = b)$라면 그 역수 $\frac{1}{X} \sim \text{IG}(\text{shape} = a, \text{scale} = b)$를 따르는 매우 중요한 관계를 가지고 있습니다. 이때 매개변수 $b$가 감마 분포의 비율 매개변수와 역감마 분포의 척도 매개변수라는 두 가지 다른 역할을 수행한다는 것에 주의하셔야합니다.
6 경험적 분포(Empirical Distribution)
우리가 어떤 분포 $p(X)$에서 추출된 데이터 샘플 집합을 가지고 있다고 가정하겠습니다. 즉, $\mathcal{D} = \{ x^{(1)}, x^{(2)}, \dots, x^{(N)} \}$이라는 데이터 샘플들을 가지고 있습니다. 그러면 저희는 이 샘플들을 이용해 원래의 PDF를 근사적으로 표현할 수 있습니다. 이를 위해 각 샘플 위치에 델타 함수를 놓아 다음과 같이 표현할 수 있습니다.
$$\hat{p}_{N}(x) = \frac{1}{N} \sum_{n = 1}^{N} \delta_{x^{(n)}}(x)$$
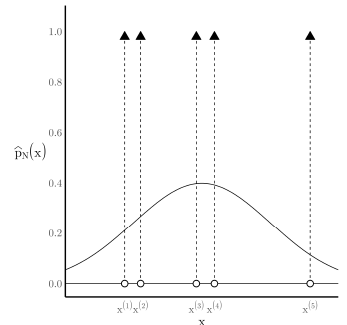
이와 같이 데이터셋 $\mathcal{D}$로부터 근사된 확률분포를 경험적 분포(empirical distribution)라고 부릅니다. 예시로, 샘플의 개수가 $N=5$인 경험적 분포가 위 그림에 나와 있습니다.
5.1 경험적 누적분포함수
이러한 경험적 분포의 CDF는 다음과 같이 정의됩니다
$$\hat{P}_{N}(x) = \frac{1}{N} \sum_{n = 1}^{N} \mathbb{I}(x^{(n)} \le x) = \frac{1}{N} \sum_{n = 1}^{N} u_{x^{(n)}}(x)$$
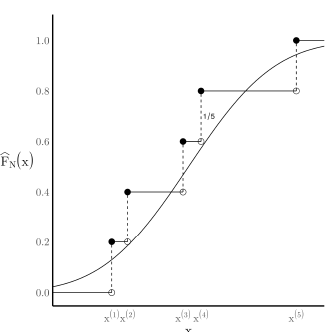
여기서 $u_{y}(x)$은 스텝 함수로 $x \le y$이면 1이고 $x < y$라면 0으로 정의되는 함수입니다. 이 경험적 누적분포함수는 "계단식" 모양으로 시각화할 수 있으며, 각 샘플 $x^{(n)}$에서 정확히 높이가 $\frac{1}{N}$만큼씩 증가합니다. 이 경험적 분포와 누적분포함수는 실제 데이터를 기반으로 분포를 근사할 때, 특히 데이터를 기반으로 하는 비모수적(non-parametric) 추정에서 매우 유용하게 사용됩니다.
6 너무 많은 분포가 존재하는 이유와 다 외워야할까?
개인적으로 이 부분에 대한 제 생각은 다음과 같습니다.
6.1 너무 많은 분포가 존재하는 이유
현실 세계에서는 다양한 형태의 데이터가 존재합니다. 예를 들면:
- 키, 몸무게와 같은 연속형 데이터 → 정규분포(Gaussian) 사용
- 확률이나 비율(0~1 사이) 데이터 → 베타(Beta) 분포 사용
- 사건 발생 간격(시간 데이터) → 지수(Exponential) 분포 사용
- 독립적인 사건들의 빈도 → 포아송(Poisson) 분포 사용
- 극단적인 이상치가 존재할 때 → 코시(Cauchy)나 스튜던트(Student) 분포 사용
즉, 데이터의 특징에 따라 적합한 분포가 달라지기 때문에 다양한 분포를 알고 있어야 합니다. 그리고 특히 베이지안 통계나 머신러닝 분야에서는 데이터를 설명하는 사전 지식을 모델링할 때 여러 분포가 자주 쓰입니다. 각 분포는 서로 다른 형태의 사전 지식을 나타내기 때문에, 이를 잘 활용하면 보다 강력한 모델링이 가능합니다.
- 양수값만 가질 수 있는 데이터는 감마(Gamma) 분포로,
- 양수 중에서도 무거운 꼬리를 가진 분포는 역감마(Inverse Gamma) 분포로 표현할 수 있습니다.
또한, 여러 분포를 이해하면 통계적 방법론을 이해할 때의 배경 지식으로 작용하여, 통계 분석이 어떤 전제 조건 아래에서 이루어졌는지 잘 이해할 수 있습니다.
6.2 그럼 다 외워?
아니요. 그럴 이유는 없습니다. 중요한 것은 각 분포가 어떤 데이터나 문제 상황에서 유용한지 그 특성을 이해하는 것입니다. 실제 실무나 연구에서는 자주 사용하는 몇 가지 분포의 특성을 명확히 알고, 나머지는 필요할 때 참고자료를 찾아보면서 사용해도 충분합니다. 실제로 전통적으로 활용되는 대표적인 분포는 가우시안 분포와 베타 분포 등이 자주 활용되고 이에 파생되는 분포들은 더 찾아봐도 충분합니다. 일단은 이런게 있구나~ 하고만 넘어가셔도 충분합니다!
