어떤 변수가 유한한 개수의 범주(클래스, 레이블) 중 하나를 취할 때, 예를 들어 $y = \{ 1, 2, \dots, C \}$ 처럼 나타낼 수 있을 때, 이를 표현하기 위한 확률 분포로 범주형 분포(Categorical distribution)를 사용합니다.
1. 정의(Definition)
범주형 분포는 일종의 이산 확률 분포로, 각 클래스마다 하나의 확률 파라미터를 가지고 있습니다. 이를 수식으로 표현하면 다음과 같습니다.
$$\text{Cat}(y | \mathbf{\theta}) = \prod_{c = 1}^{C} \theta^{\mathbb{I}(y = c)}_{c}$$
위 수식은 간단히 말해서, 특정 클래스 $c$가 선택될 확률이 $\theta_{c}$라는 의미힙니다. 즉, 클래스 $c$일 확률을 $p(y = c | \mathbf{\theta}) = \theta_{c}$로 표현하였습니다. 여기서 각 확률 파라미터 $\theta_{c}$는 $0 \le \theta \le 1$이여야하고 $\sum_{c = 1}^{C} \theta_{c} = 1$을 만족해야합니다. 이 때문에 실제로 독립적인 파라미터 개수는 전체 클래스 수 $C$에서 하나를 뺀 $C - 1$개가 됩니다.
2. 원-핫(One-hot) 표현 방식
범주형 변수를 표현할 때, 흔히 원-핫(one-hot) 벡터라는 것을 사용하기도 합니다. 원-핫 벡터는 클래스 수 $C$ 만큼의 길이를 가지며, 해당하는 클래스의 위치에만 1이 있고 나머지 모든 값은 0인 벡터입니다. 이 역시 딥 러닝 공부하셨던 분들은 다중 클래스 분류문제에서 자주 본 용어일 겁니다. 예를 들어, 클래스가 3개($C = 3$)일 때는 다음과 같이 표기합니다.
- 클래스 1 → (1, 0, 0)
- 클래스 2 → (0, 1, 0)
- 클래스 3 → (0, 0, 1)
이런 식으로 표현하는 방식을 원-핫 인코딩이라고 부릅니다. 원-핫 벡터를 이용하면 범주형 분포를 다음과 같이 나타낼 수도 있습니다.
$$\text{Cat}(\mathbf{y} | \mathbf{\theta}) = \prod_{c = 1}^{C} \theta^{y_{c}}_{c}$$
여기서 $y_{c}$는 벡터 $\mathbf{y}$의 $c$번째 값으로 원-핫 벡터이기 때문에 특정 클래스에서만 1이고 나머지는 모두 0입니다.
3. 다항 분포(Multinomial distribution)로의 확장
범주형 분포는 다항 분포의 특수한 경우라고 할 수 있습니다. 다항 분포는 쉽게 말해, 범주형 시행을 여러 번 반복했을 때 각 클래스가 몇 번 등장했는지를 표현한 분포입니다. 이전 포스팅에서 설명한 베르누이 분포와 이항 분포 사이의 관계와 동일합니다!
더 구체적으로 설명하자면 $C$개의 면이 있는 주사위를 $N$번 던졌을 때 각 면이 나온 횟수를 세는 상황을 생각해볼 수 있습니다. 이렇게 각 클래스의 등장 횟수를 세는 벡터를 $\mathbf{y} = (y_{1}, y_{2}, \dots, y_{C})$ 라고 하면, 이때의 확률 분포가 바로 다항 분포입니다. 다항 분포는 다음과 같은 수식으로 정의됩니다.
$$\mathcal{M}(\mathbf{y}|N, \mathbf{\theta}) = \begin{pmatrix} N \\ y_{1} \dots y_{C} \end{pmatrix} \prod_{c = 1}^{C} \theta^{y_{c}}_{c} = \begin{pmatrix} N \\ N_{1} N_{2} \dots, N_{C} \end{pmatrix} \prod_{c = 1}^{C} \theta^{N_{c}}_{c}$$
여기서, $\theta_{c}$는 각 클래스 $c$가 나올 확률입니다. $y_{c}$는 클래스 $c$가 등장한 횟수이며 모든 클래스의 등장 횟수를 합하면 총 $N$번의 시행횟수가 나옵니다. 즉, $\sum_{c = 1}^{C} N_{c}$이죠. 여기서 다항계수 $\begin{pmatrix} N \\ N_{1}, N_{2}, \dots, N_{C} \end{pmatrix} = \frac{N!}{N_{1}!N_{2}! \dots N_{C}!}$로 정의됩니다. 수식을 보시면 아시겠지만 여기서 $N = 1$, 즉 시행횟수가 한 번이라면 이는 범주형 분포와 동일해지므로 다항 분포는 여러 번의 범주형 시행 결과를 하나로 표현한 확장된 형태라고 할 수 있습니다.
4. 소프트맥스 함수(Softmax Function)
특정 조건(입력값 $x$) 이 주어졌을 때, 클래스 $y$ 가 나타날 확률을 표현하기 위해 범주형 분포(Categorical Distribution)를 다음과 같이 사용할 수 있습니다. 지난 포스팅에서는 이진클래스였기 때문에 베르누이 분포로 사용하였지만 이번에는 다중클래스이기 때문에 범주형 분포를 사용하여 표현하는 것입니다!
$$p(y|\mathbf{x}, \mathbf{\theta}) = \text{Cat}(y|f(\mathbf{x}; \mathbf{\theta}))$$
이 표현을 시행횟수가 1인 다항 분포($N = 1$)를 이용해 다음과 같이 나타내는 것도 가능합니다.
$$p(y|\mathbf{x}, \mathbf{\theta}) = \mathcal{M}(\mathbf{y}| 1, f(\mathbf{x}; \mathbf{\theta}))$$
여기서 확률분포의 성질 상 함수 $f(\mathbf{x}; \mathbf{\theta})$는 $0 \le f_{c}(\mathbf{x}; \mathbf{\theta}) \le 1$이고 $\sum_{c = 1}^{C} f_{c}(\mathbf{x}; \mathbf{\theta}) = 1$이여야합니다. 하지만, 하지만 함수 $f(\mathbf{x}; \mathbf{\theta})$가 위의 조건을 항상 만족하도록 직접 확률값을 출력하는 것은 어렵습니다. 이를 해결하기 위해 흔히 사용하는 방법이 바로 소프트맥스(Softmax) 함수입니다.
4.1 소프트맥스 함수의 정의
소프트맥스 함수는 로짓(logit)이라는 임의의 값을 받아 확률 분포 형태로 변환해주는 함수입니다. 이를 수식으로 나타내면 다음과 같습니다.
$$\text{softmax}(\mathbf{a}) = \left[ \frac{e^{a_{1}}}{\sum_{c^{'}=1}^{C} e^{a_{c}^{'}}}, \dots, \frac{e^{a_{C}}}{\sum_{c^{'}=1}^{C} e^{a_{c^{'}}}} \right]$$
즉, 각 원소 $a_{c}$를 지수함수($e^{a_{c}}$)를 사용해 모두 양수로 변환하고 그 값을 전체 합으로 나누어 정규화(normalization)한 것입니다. 이렇게 되면 원래의 값은 어떠한 실수값 $\mathbb{R}^{C}$더라도 최종값은 $[0, 1]^{C}$ 이 되며, 전체 합이 반드시 1이 됩니다. 이 때 소프트맥스 함수의 입력값인 벡터 $a$를 로짓(logits)이라고 부르며, 로짓은 확률값을 나타내기 전에 존재하는 원시(raw) 형태의 점수입니다. (로짓은 로짓스틱 회귀(logistic regression)에서 사용되는 로그 오즈(log odds)의 개념을 일반화한 것으로 생각할 수 있습니다.) 이 역시 딥 러닝 공부하셨던 분들은 잘 아실 거 같네요.
4.2 왜 소프트맥스인가?
소프트맥스라는 이름이 붙은 이유는 이 함수가 일종의 부드러운(soft) 아그맥스(argmax) 함수처럼 작동하기 때문입니다. 아그맥스(argmax)는 여러 값 중 가장 큰 값을 선택하는 함수인데, 소프트맥스 함수는 이를 부드럽게 연속적인 확률 값으로 표현해줍니다. 이 특성을 더 이해하기 위해, 각 로짓값 $a_{c}$를 어떤 상수 $$ (온도, temperature)로 나누어준 뒤, $T$ 값을 조절하면 어떻게 되는지 살펴볼 수 있습니다.
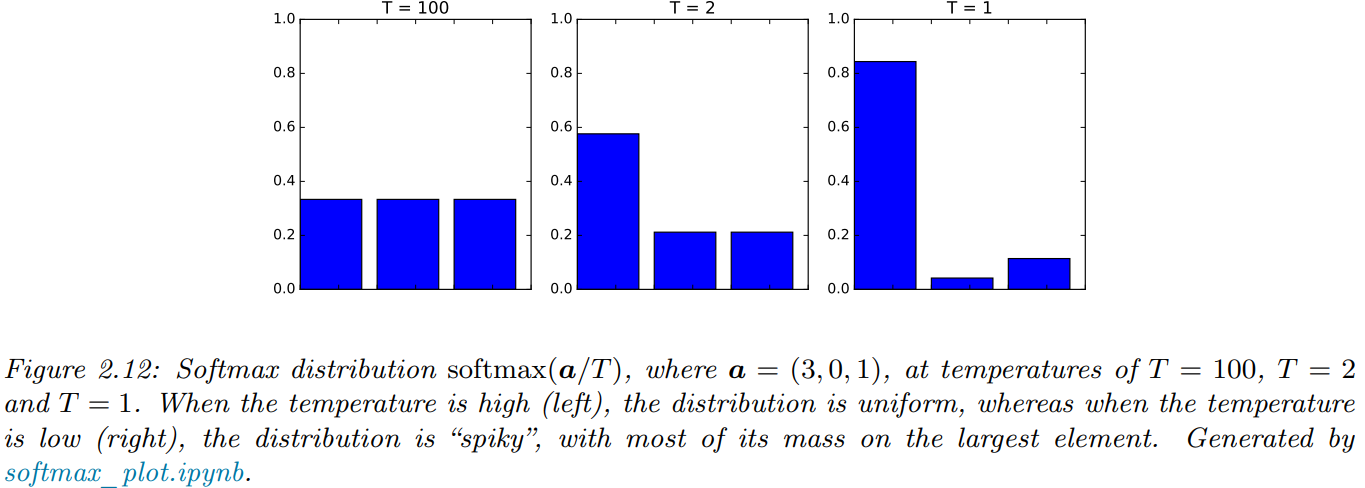
온도 $T$가 매우 작은 값이 되면 소프트맥스의 값은 가장 큰 로짓값을 가진 클래스에서만 확률 1을 부여하고, 나머지 클래스 확률은 0으로 수렴하게 됩니다. 이러한 현상을 승자 독식(winner takes all)이라고 표현하기도 합니다. 즉, 수식으로 나타내면$c = \text{argmax}_{c^{'}}(a_{c^{'}})$일 때 $\text{softmax}(\frac{\mathbf{a}}{T})_{c} = 1$이고 아니라면 $\text{softmax}(\frac{\mathbf{a}}{T})_{c} = 0$이 됩니다. 반대로 온도 $T$가 매우 큰 값일 경우 모든 클래스에 거의 균등한 확률값을 할당하게 되어 확률 분포가 평평해지게 됩니다.
5. 다중 클래스 로지스틱 회귀(Multiclass Logistic Regression)
앞서 정의한 범주형 분포와 소프트맥스 함수를 이용하면 다중 클래스 분류 모델을 쉽게 만들 수 있습니다. 여기서 선형 예측(linear predictor)을 사용하는 경우를 생각해 봅시다. 입력값 $\mathbf{x}$가 $D$차원의 벡터라고 할 때, 클래스가 $C$개라면 다음과 같은 선형 예측 함수를 정의할 수 있습니다.
$$f(\mathbf{x}; \mathbf{\theta}) = \mathbf{W} \mathbf{x} + \mathbf{b}$$
여기서 $\mathbf{W} \in \mathbb{R}^{C \times D}$인 가중치 행렬이고 $\mathbf{b} \in \mathbb{R}^{C}$는 편향(bias) 벡터입니다. 이 함수를 소프트맥스 함수에 넣어 최종적으로 확률값을 얻으면, 다음과 같은 형태가 됩니다.
$$p(\mathbf{y}| \mathbf{x}; \mathbf{\theta}) = \frac{e^{a_{c}}}{\sum_{c^{'} = 1}^{C} e^{a_{c^{'}}}}$$
이 모델을 바로 다중 클래스 로지스틱 회귀(Multinomial logistic regression)라고 부릅니다.
5.1 이항 로지스틱 회귀(Binary Logistic Regression)와의 관계
클래스가 딱 두 개($C = 2$) 만 있을 때는, 이 다중 클래스 로지스틱 회귀가 이항 로지스틱 회귀(Binary logistic regression)로 축소됩니다. 이를 확인해 봅시다. 두 클래스만 있다고 하면, 소프트맥스 함수는 다음과 같이 표현될 수 있습니다.
$$\text{softmax}(\mathbf{a})_{0} = \frac{e^{a_{0}}}{e^{a_{0}} + e^{a_{1}}} = \frac{1}{1 + e^{a_{1} - a_{0}}} = \sigma(a_{0} - a_{1})$$
여기서 $\sigma(\cdot)$은 로지스틱 시그모이드(logistic sigmoid) 함수로 정의됩니다. 즉, 클래스가 두 개뿐이라면, 다중 클래스 로지스틱 회귀를 굳이 쓸 필요 없이, 그냥 두 로짓(logit)의 차이 $a = a_{1} - a_{0}$를 예측하는 하나의 가중치 벡터 $\mathbf{w}$만 사용하면 됩니다. 반면, 다중 클래스 로지스틱 회귀를 그대로 두 클래스에 적용하면 클래스마다 하나의 가중치 벡터를 따로 갖게 되어 가중치가 중복되는(over-parameterized) 현상이 발생할 수 있습니다. 이 경우 해석이 어렵긴 하지만, 결과적으로 얻어지는 예측 결과 자체는 동일합니다. 이러한 개념에 대해서는 향후에 더 자세히 살펴보도록 하겠습니다.
5.2 다중 클래스 로지스틱 회귀의 예시
이를 더 직관적으로 보기 위해 3가지 클래스(품종)를 가진 아이리스(iris) 데이터셋을 예로 들어보겠습니다. 이 데이터셋에서 두 개의 특징(feature)만 사용하여 다중 클래스 로지스틱 회귀 모델을 학습시키면, 각 클래스 사이의 경계가 직선으로 나타나게 됩니다.
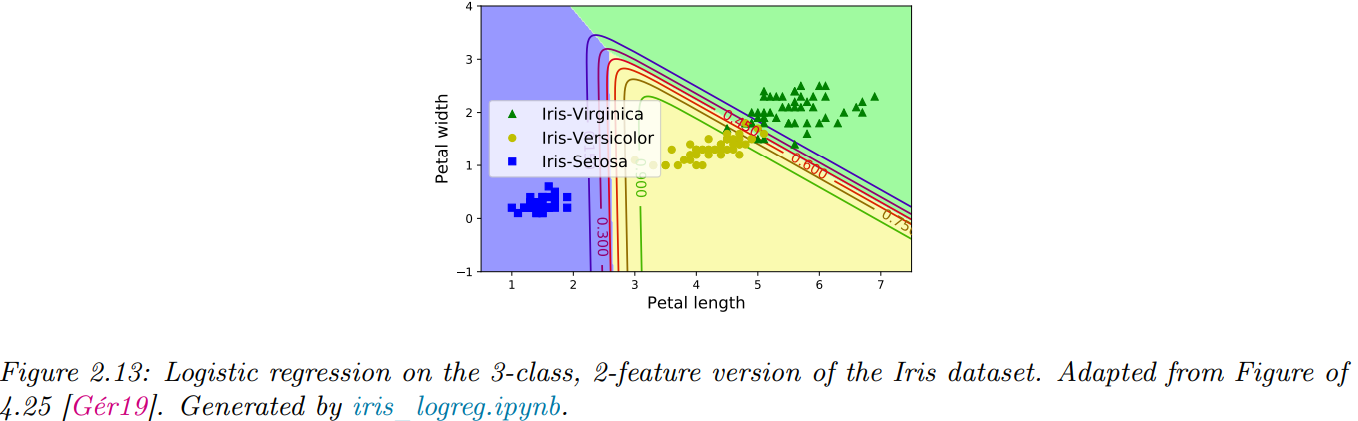
이처럼 다중 클래스 로지스틱 회귀는 기본적으로 각 클래스 간 경계를 선형(linear)으로 결정짓습니다. 만약 보다 복잡하고 비선형적인 경계를 얻고자 한다면, 특징을 변환하는 방법(예: 다항식 변환)을 사용하면 됩니다. 이 부분은 향후에 더 자세히 살펴보도록 하겠습니다.
6. 로그-합-지수(Log-sum-exp) 기법
이번 절에서는 소프트맥스 분포를 실제로 구현할 때 매우 중요한 수치적 안정성(numerical stability) 문제를 해결하기 위한 기법을 소개합니다. 소프트맥스 함수는 클래스 $c$ 의 확률을 계산할 때 다음과 같은 형태를 가집니다.
$$p_{c} = p(y = c|\mathbf{x}) = \frac{e^{a_{c}}}{Z(\mathbf{a})} = \frac{e^{a_{c}}}{\sum_{c^{'} = 1}^{C} e^{a_{c^{'}}}}$$
여기서 $a = f(\mathbf{x}; \mathbf{\theta})$ 를 로짓이라 부르고 $Z(\mathbf{a})$ 를 정규화 상수(partition function) 라고 합니다.
6.1 왜 수치적 안정성 문제가 발생할까?
실제로 이 정규화 상수 $Z(\mathbf{a})$ 를 컴퓨터에서 계산할 때 큰 숫자 문제가 발생할 수 있습니다. 예를 들어, 다음과 같은 로짓 벡터를 가정해 봅시다. $\mathbf{a} = (0, 1, 0)$이라면 $Z(\mathbf{a}) = e^{0} + e^{1} + e^{0} = 1 + 2.71 + 1 = 4.71$로 문제없이 계산됩니다. 하지만, $\mathbf{a} = (1000, 1001, 1000)$일 경우 $e^{1000}$ 그리고 $e^{1001}$와 같은 큰 값은 컴퓨터가 처리할 수 없어 무한대로 취급됩니다. 실제로 자주 사용하는 파이썬 라이브러리 중 하나인 numpy에서 64비트 실수를 사용해도 np.exp($e^{1000}$) = $\inf$가 나오게 됩니다. 이는 매우 작은 숫자도 마찬가지죠. 즉, 아주 큰 값이 등장하면 숫자가 무한대로 발산하고, 아주 작은 값은 0에 너무 가까워져서 정보가 사라지게 됩니다.
6.2 로그-합-지수(Log-sum-exp) 트릭
이러한 수치적 안정성 문제를 해결하기 위해서 로그-합-지수(Log-sum-exp) 트릭을 사용합니다. 이 트릭은 다음과 같은 중요한 항등식을 이용합니다.
$$\text{log} \left( \sum_{c = 1}^{C} e^{a_{c}} \right) = m + \text{log} \left( \sum_{c = 1}^{C} e^{a_{c} - m} \right)$$
여기서 $m$ 은 아무 값이나 가능하지만, 일반적으로 로짓 벡터에서 가장 큰 값인 $m = \text{max}_{c} a_{c}$ 를 선택합니다. 이렇게 하면 지수 함수의 입력값이 항상 0 이하로 제한되므로, 계산 과정에서 값이 무한대로 발산하는 것을 방지할 수 있습니다. 이렇게 정의된 로그-합-지수(Log-sum-exp, LSE) 함수는 다음과 같습니다.
$$\text{lse}(\mathbf{a}) = \text{log} \left( \sum_{c = 1}^{C} e^{a_{c}} \right)$$
이를 이용해 클래스 확률을 계산하면 다음과 같습니다.
$$p(y = c|\mathbf{x}) = e^{a_{c} - \text{lse}(\mathbf{a})}$$
이렇게 하면 수치적으로 안정적인 확률값을 얻을 수 있습니다.
6.3 실제 크로스엔트로피(Cross-entropy) 손실 계산 시의 적용법
로짓 값을 확률값으로 변환한 뒤 크로스엔트로피 손실(cross-entropy loss)을 계산할 수도 있지만, 실제로는 숫자적 안정성과 효율성을 위해 로짓 값을 직접 손실 함수에 전달하여 계산하는 방식을 흔히 사용합니다. 예를 들어, 클래스가 두 개인 경우의 크로스엔트로피 손실은 다음과 같이 정의됩니다.
$$\mathcal{L} = - [\mathbb{I}(y = 0)\text{log}(p_{0}) + \mathbb{I}(y = 1) \text{log}(p_{1})]$$
이때 각 클래스의 확률 $p_{0}$와 $p_{1}$ 의 로그값을 로짓을 이용해 바로 계산하면 다음과 같습니다.
$$\text{log}(p_{1}) = \text{log}\left( \frac{1}{1 + e^{-a}} \right) = 0 - \text{lse}([0, -a])$$
$$\text{log}(p_{0}) = 0 - \text{lse}([0, +a])$$
이렇게 하면 굳이 확률값을 계산하는 중간 단계를 거치지 않고, 직접 로짓 값을 사용하여 숫자적으로 안정적이고 효율적으로 손실 함수를 계산할 수 있습니다.
