확률변수(random variable)는 관심 있는 어떤 불확실한 값을 나타낼 때 사용합니다. 예를 들어 주사위를 던졌을 때 나오는 숫자나 현재 집 밖의 기온처럼, 값이 미리 정해지지 않았거나 변할 수 있는 경우가 이에 해당됩니다. 확률변수를 보통 $X$라고 표현하며, 가능한 값들의 집합을 표본공간(sample space) 또는 상태공간(state space)이라고 합니다. 하나의 사건(event)이란 이 표본공간에서 특정 결과들의 집합을 의미합니다. 예컨대, 주사위를 던졌을 때 나오는 숫자를 확률변수 $X$라 하면, 표본공간은 $X = \{ 1, 2, 3, 4, 5, 6 \}$이며, ‘1이 나오는 사건’은 $X = 1$, ‘홀수가 나오는 사건’은 $X = \{ 1, 3, 5 \}$, ‘1부터 3까지의 숫자가 나오는 사건’은 $1 \le X \le 3$와 같이 나타낼 수 있습니다.
1. 이산 확률변수(Discrete Random Variables)
표본공간이 유한하거나 셀 수 있는 무한한 원소들로 구성되어 있다면, 이 확률변수를 이산 확률변수(discrete random variable)라고 부릅니다. 이산 확률변수의 특정 값 $x$에 대한 사건의 확률을 $\text{Pr}(X = x)$로 나타내며, 이러한 확률들을 계산해 주는 함수를 확률 질량 함수(probability mass function, pmf)라고 정의합니다. 수식으로는 다음과 같이 표현합니다:
$$p(x) = \text{Pr}(X = x)$$
이 확률 질량 함수는 두 가지 중요한 특성을 만족해야 합니다:
1). 모든 $x$에 대해 $0 \le p(x) \le 1$
2). 표본공간에 있는 모든 값들에 대한 확률의 합이 1이어야 함. 즉 $\sum_{x \in X} p(x) = 1$

표본공간이 유한한 값들로 구성되어 있을 경우, 이 pmf는 그림 2.1과 같이 히스토그램 형태로 시각적으로 나타낼 수 있습니다. 예를 들어, 다음과 같은 두 가지 경우가 있습니다:
- 균등분포(uniform distribution): 모든 값의 확률이 동일하게 $p(x) = \frac{1}{4}$로 설정됩니다.
- 퇴화 분포(degenerate distribution): 특정 값 하나에만 확률이 몰려 있으며 나머지 값들에 대해서는 확률이 0인 분포로, 예를 들어 $p(x) = \mathbb{I}(x = 1)$형태로 표현됩니다. 여기서, $\mathbb{I}(\cdot)$는 조건이 참이면 1, 그렇지 않으면 0을 나타내는 지시함수(indicator function)입니다. 이러한 퇴화 분포는 확률변수가 항상 일정한 값을 가지는 경우를 나타내며, 따라서 확률변수가 꼭 변하는 값만을 의미하는 것은 아니라는 것을 알 수 있습니다.
2. 연속 확률변수 (Continuous Random Variables)
만약 어떤 확률변수 $X$가 실수 값 전체를 대상으로 할 수 있다면, 이를 연속 확률변수(continuous random variable) 라고 합니다. 이때는 더 이상 확률변수가 취할 수 있는 값들을 유한하거나 셀 수 있는 집합으로 나타낼 수 없습니다. 하지만 실수 전체를 수많은 구간(interval)으로 나누고 각 구간에 대해 확률을 할당하면, 앞서 언급한 이산 확률변수와 유사한 방식으로 다룰 수 있습니다. 직관적으로는, 구간의 크기를 점점 줄여서 특정 값을 가질 확률을 나타내는 방식을 사용할 수 있습니다.
2.1. 누적분포함수 (Cumulative Distribution Function, cdf)
먼저, $A = (X \le a), B = (X \le b), C = (a \le X \le b)$로 3개의 사건을 정의하겠습니다. 여기서, $a < b$입니다. 사건 $B$는 사건 $A$와 사건 $C$의 합집합이고 이 둘의 서로 배타적이기 때문에 확률의 덧셈법칙에 따라 다음과 같이 표현됩니다.
$$\text{Pr}(B) = \text{Pr}(A) + \text{Pr}(C)$$
따라서, 사건 $C$의 확률은 다음과 같습니다.
$$\text{Pr}(C) = \text{Pr}(B) - \text{Pr}(A)$$
일반적으로, 확률변수 $X$의 누적분포함수(Cumulative Distribution Function, cdf) 는 다음과 같이 정의됩니다. (여기서 cdf는 대문자 $P$로 나타냅니다.)
$$P(x) = \text{Pr}(X \le x)$$
이 정의를 이용하면 어떤 구간에 속할 확률을 간단히 다음처럼 구할 수 있습니다.
$$\text{Pr}(a < X \le b) = P(b) - P(a)$$

누적분포함수는 항상 단조 증가(monotonically non-decreasing)합니다. 누적분포함수의 대표적인 예시로 그림 2.2.(a)와 같이 표준정규분포 $\mathcal{N}(x|0, 1)$을 나타낸 그래프를 생각할 수 있습니다.
2.2. 확률밀도함수 (Probability Density Function, pdf)
누적분포함수 $P(x)$ 를 미분한 것을 확률밀도함수(Probability Density Function, pdf) 라고 정의합니다. (이 미분값이 항상 존재하지는 않으며, 그럴 경우에는 pdf가 정의되지 않습니다.)
$$p(x) = \frac{d}{dx} P(x)$$
확률밀도함수의 예로는 그림 2.2.(b)와 같이 단변량 가우시안 분포가 있으며, 일반적으로 다음과 같이 주어진 구간에 포함될 확률을 계산할 수 있습니다.
$$\text{Pr}(a < X \le b) = \int_{a}^{b} p(x) \; dx = P(b) - P(a)$$
구간의 크기가 점점 작아질 때, 확률은 다음과 같이 근사적으로 표현될 수 있습니다.
$$\text{Pr}(x < X \le x + dx) \approx p(x) dx$$
즉, 직관적으로 이는 확률변수 $X$가 아주 작은 구간 $[x, x + dx]$ 내에 있을 확률이 확률밀도함수 값 $p(x)$ 와 구간의 너비 $dx$의 곱과 같다는 의미입니다.
2.3. 분위수(Quantiles)
누적분포함수(CDF) $P(x)$가 엄밀히 단조 증가(strictly monotonically increasing) 하는 경우, 역함수를 정의할 수 있는데, 이를 역 누적분포함수(inverse CDF) 혹은 백분위함수(percent point function, ppf), 또는 분위수함수(quantile function) 라고 부릅니다.
확률변수 $X$의 누적분포함수가 $P(x)$라면 역함수 $P^{-1}(q)$ 는 다음과 같은 조건을 만족하는 값 $x_{q}$를 의미합니다.
$$\text{Pr}(X \le x_{q}) = q$$
이 값을 $q$번째 분위수라고 합니다. 특히, $P^{-1}(0.5)$는 중앙값(median) 으로서, 확률 분포의 절반이 중앙값보다 작고 나머지 절반이 중앙값보다 크도록 합니다. 마찬가지로 $P^{-1}(0.25)$와 $P^{-1}(0.75)$는 각각 하위 사분위수(lower quartile) 와 상위 사분위수(upper quartile) 로 불립니다.
예를 들어, 표준정규분포 $\mathcal{N}(0, 1)$의 누적분포함수를 $\Phi(x)$, 그 역함수를 $\Phi^{-1}$ 라고 하면, 그림 2.2.(b)에서 나타낸 바와 같이 다음과 같은 관계가 성립합니다.
- 왼쪽에서부터 점 $\Phi^{-1}(\frac{\alpha}{2})$ 까지의 영역에는 전체 확률질량의 $\frac{\alpha}{2}$ 가 포함됩니다.
- 대칭성으로 인해, 오른쪽으로부터 점 $\Phi^{-1}(1 - \frac{\alpha}{2})$ 까지의 영역에도 전체 확률질량의 $\frac{\alpha}{2}$ 가 포함됩니다.
결과적으로 중심 영역 $\left( \Phi^{-1}(\frac{\alpha}{2}), \Phi^{-1}(1 - \frac{\alpha}{2}) \right)$ 는 전체 확률질량의 $1 - \alpha$를 포함합니다. 특히, $\alpha = 0.05$로 설정하면, 95% 확률 질량을 갖는 중심 구간은 다음과 같이 나타납니다.
$$ \left( \Phi^{-1}(0.025), \Phi^{-1}(0.975) \right) = (-1.96, 1.96)$$
이를 평균이 $\mu$이고 분산이 $\sigma^{2}$인 정규분포 $\mathcal{N}(\mu, \sigma^{2})$으로 일반화하면, 95% 중심 구간은 다음과 같습니다.
$$(\mu - 1.96 \sigma, \mu + 1.96 \sigma)$$
이는 흔히 $\mu \pm 2\sigma$로 근사되어 사용되기도 합니다.
2.4. 관련 확률변수들의 집합(Sets of related random variables)
이제, 서로 관련된 확률변수들에 대한 분포를 살펴보겠습니다. 먼저 두 개의 확률변수 $X, Y$ 가 있다고 생각해봅시다. 이 두 확률변수에 대한 결합분포(Joint distribution)는 다음과 같이 정의됩니다.
$$p(x, y) = p(X = x, Y = y)$$
만약 두 확률변수가 유한한 개수의 값을 가질 경우, 결합분포를 모든 항목의 합이 1이 되는 2차원 표로 나타낼 수 있습니다. 예를 들어 다음과 같은 두 개의 이진변수(binary variables)를 고려해 봅시다.
| $P(X, Y)$ | $Y = 0$ | $Y = 1$ |
| $X = 0$ | 0.2 | 0.3 |
| $X = 1$ | 0.3 | 0.2 |
만약 두 변수가 서로 독립(independent)이라면, 결합분포는 각 변수가 가진 주변분포(marginal distributions)의 곱으로 표현됩니다. 이때, 위의 2차원 표는 두 개의 1차원 벡터의 곱으로 표현됩니다. 결합분포가 주어졌을 때, 확률변수 하나의 주변분포(Marginal distribution) 는 다음과 같이 계산할 수 있습니다. 여기서 주변분포라는 용어는, 행과 열의 합계를 표의 주변(margin)에 기록했던 회계 관습에서 비롯되었습니다.
$$p(X = x) = \sum_{y} p(X = x, Y = y)$$
이때 합산은 가능한 모든 $Y$ 값들에 대해 이뤄집니다. 이를 합의 규칙(sum rule) 또는 전체확률 규칙(rule of total probability) 이라고도 합니다. 예를 들어, 위 표에서 계산해 보면 다음과 같습니다.
- $p(X = 0) = 0.2 + 0.3 = 0.5$
- $p(Y = 0) = 0.2 + 0.3 = 0.5$
또한, 한 변수의 값이 주어졌을 때 다른 변수의 조건부 분포(Conditional distribution) 는 다음과 같이 정의됩니다.
$$p(Y = y | X = x) = \frac{p(X = x, Y = y)}{p(X = x)}$$
이를 다시 정리하면 다음과 같은 곱의 규칙(product rule) 을 얻습니다.
$$p(X = x, Y = y) = p(Y = y | X = x)p(X = x)$$
곱의 규칙을 확장하여 $D$ 개의 변수에 대한 결합분포를 표현하면, 다음과 같은 연쇄 규칙(chain rule) 이 됩니다.
$$p(x_{1:D}) = p(x_{1})p(x_{2}|x_{1})p(x_{3}|x_{1}, x_{2}) \cdots p(x_{D}|x_{1:D-1})$$
이는 조건부 분포들의 곱으로부터 고차원의 결합분포를 구성할 수 있는 방법을 제공합니다. 이 내용에 대해서는 향후에 더 자세히 다룰 예정입니다.
2.5. 독립성과 조건부 독립성 (Independence and Conditional Independence)
두 확률변수 $X$와 $Y$ 가 서로 영향을 주지 않고 독립적으로 존재할 때, 이 둘은 (무조건적) 독립(unconditional independence) 또는 주변 독립(marginal independence)이라고 하며, 이를 기호로 $X \perp Y$로 나타냅니다. 이때 두 변수의 결합 확률분포(joint distribution)는 각 주변분포(marginal distributions)의 곱으로 나타낼 수 있습니다. 수식으로 표현하면 다음과 같습니다.
$$X \perp Y \Leftrightarrow p(X, Y) = p(X)p(Y)$$
일반적으로 여러 확률변수 $X_{1}, \dots, X_{n}$이 **상호 독립(mutually independent)**이라는 것은 이들 중 임의의 부분 집합에 대한 결합분포가 해당 개별 변수들의 주변분포 곱으로 표현될 수 있다는 것을 의미합니다. 이를 수식으로 쓰면 모든 부분집한 $\{X_{1}, \dots, X_{m}\} \subset \{ X_{1}, \dots, X_{n} \}$에 대해 $p(X_{1}, \dots, X_{m}) = \prod_{i = 1}^{m} p(X_{i})$가 성립할 때, $X_{1}, \dots, X_{n}$은 상호 독립이라고 부릅니다.
예를 들어, 세 개의 변수 $X_{1}, X_{2}, X_{3}$ 이 상호 독립이라는 조건은 다음과 같은 조건들을 만족해야 함을 의미합니다.
- $p(X_{1}, X_{2}, X_{3})= p(X_{1})p(X_{2})p(X_{3})$
- $p(X_{1}, X_{2})= p(X_{1})p(X_{2})$
- $p(X_{2}, X_{3})= p(X_{2})p(X_{3})$
- $p(X_{1}, X_{3})= p(X_{1})p(X_{3})$
현실에서 무조건적 독립성(unconditional independence)은 매우 드뭅니다. 왜냐하면 대부분의 변수들은 서로 직간접적으로 영향을 미치기 때문입니다. 그러나 흔히 변수 간의 영향이 직접적인 것이 아니라 다른 변수를 통해 간접적으로 이루어집니다. 이러한 경우 우리는 두 확률변수 $X$와 $Y$가 어떤 변수 $Z$ 가 주어진 조건하에서 독립이라고 말하며, 이를 조건부 독립성(conditional independence)이라 부릅니다. 수식으로 표현하면 다음과 같습니다.
$$X \perp Y | Z \Leftrightarrow p(X, Y|Z) = p(X|Z)p(Y|Z)$$
이 조건부 독립성의 가정은 $X - Z - Y$ 와 같은 형태의 그래프로 나타낼 수 있는데, 이 그래프는 $X$와 $Y$ 사이의 모든 의존관계가 $Z$ 를 통해서만 이루어진다는 직관을 시각적으로 표현합니다. 이러한 형태의 그래프를 확장하면 더욱 복잡한 결합 확률분포를 정의할 수 있으며, 이를 그래프 모델(Graphical Models)이라고 합니다. 이 개념은 향후에 더 자세히 다룰 예정입니다.
2.6. 분포의 모멘트 (Moments of a distribution)
이 절에서는 확률분포(연속 또는 이산 분포)에서 도출할 수 있는 여러 가지 요약 통계량을 살펴보겠습니다.
2.6.1 분포의 평균 (Mean of a distribution)
확률분포의 가장 친숙한 특성 중 하나는 바로 평균(mean) 또는 기댓값(expected value)이며, 흔히 $\mu$로 나타냅니다.
- 연속 확률변수의 평균: $\mathbb{E}[X] = \int_{\mathcal{X}} x p(x) \; dx$ ( 만약 적분 값이 유한하지 않으면 평균은 정의되지 않습니다. )
- 이산 확률변수의 평균: $\mathbb{E}[X] = \sum_{x \mathcal{X}} xp(x)$
기댓값은 선형 연산자로서, 다음과 같은 기댓값의 선형성(linearity of expectation) $\mathbb{E}[aX + b] = a\mathbb{E}[X] + b$를 만족합니다. 따라서, 여러 개의 확률변수들의 합에 대한 기댓값은 $\mathbb{E}\left[ \sum_{i = 1}^{n} X_{i} \right] = \sum_{i = 1}^{n} \mathbb{E}[X_{i}]$와 같이 표현할 수 있습니다.
만약 이 확률변수들이 서로 독립이라면, 그 곱의 기댓값은 $\mathbb{E}\left[ \prod_{i = 1}^{n} X_{i} \right] = \prod_{i = 1}^{n} \mathbb{E}[X_{i}]$ 와 같이 표현할 수 있습니다.
2.6.2 분포의 분산 (Variance of a distribution)
분포의 분산(variance)은 분포의 ‘퍼짐 정도(spread)’를 나타내며, 일반적으로 $\sigma^{2}$ 로 표기합니다. 다음과 같이 정의됩니다.
$$\begin{align} \mathbb{V}[X] &= \mathbb{E}[(X - \mu)^{2}] \\ &= \int (x - \mu)^{2} p(x) \; dx \\ &= \int x^{2}p(x) \; dx + \mu^{2} \int p(x) \; dx - 2\mu \int xp(x) \; dx \\ &= \mathbb{E}[X^{2}] - \mu^{2} \end{align}$$
이로 인해 $\mathbb{E}[X^{2}] = \sigma^{2} + \mu^{2}$이라는 결과도 얻을 수 있습니다. 여기서 분산의 양의 제곱근을 **표준편차(standard deviation)**라 하며, 확률변수 $X$와 같은 단위를 갖기 때문에 실용적으로 유용합니다.
$$\text{std}[X] = \sqrt{\mathbb{V}[X]} = \sigma$$
확률변수의 선형변환에 대한 분산은 $\mathbb{V}[aX + b] = a^{2}\mathbb{V}$로 표현되며 서로 독립인 $n$ 개의 확률변수들의 합에 대한 분산은 $\mathbb{V}\left[ \sum_{i = 1}^{n} X_{i} \right] = \sum_{i = 1}^{n} \mathbb{V}[X_{i}]$로 각각 분산의 합과 같습니다.
하지만, 이들의 곱에 대한 분산은 다음과 같은 복잡한 형태로 나타납니다.
$$\begin{align} \mathbb{V} \left[ \prod_{i = 1}^{n} X_{i} \right] &= \mathbb{E} \left[ \left( \prod_{i = 1}^{n} X_{i} \right)^{2} \right] - \left( \mathbb{E} \left[ \prod_{i = 1}^{n} X_{i} \right] \right)^{2} \\ &= \mathbb{E} \left[ \prod_{i = 1}^{n} X_{i}^{2} \right] - \left( \prod_{i = 1}^{n} \mathbb{E} [X_{i}] \right)^{2} \\ &= \prod_{i = 1}^{n} \mathbb{E} \left[ X_{i}^{2} \right] - \prod_{i = 1}^{n} \left( \mathbb{E} [X_{i}] \right)^{2} \\ &= \prod_{i = 1}^{n} \left( \mathbb{V}[X_{i}] + \left( \mathbb{E}[X_{i}] \right)^{2} \right) - \prod_{i = 1}^{n} \left( \mathbb{E}[X_{i}] \right)^{2} \\ &= \prod_{i = 1}^{n} (\sigma^{2}_{i} + \mu^{2}_{i}) - \prod_{i = 1}^{n} \mu_{i}^{2} \end{align}$$
2.6.3 분포의 최빈값 (Mode of a distribution)
확률분포의 최빈값(mode)이란, 확률밀도함수(pdf) 또는 확률질량함수(pmf)에서 가장 확률이 높은 값을 의미합니다.
$$x^{*} = \text{argmax}_{x} p(x)$$
분포가 다봉(multimodal) 형태인 경우 최빈값은 유일하지 않을 수도 있습니다. 또한, 최빈값이 유일하다 해도 항상 분포를 잘 대표하지는 않습니다.
2.6.4. 조건부 모멘트 (Conditional moments)
두 개 이상의 종속된 확률변수가 있다면, 한 변수가 주어졌을 때 다른 변수의 모멘트를 계산할 수 있습니다. 대표적으로 반복 기대 법칙(law of iterated expectations) 또는 전체 기대 법칙(law of total expectation)이 있습니다.
$$\mathbb{E}[X] = \mathbb[E]_{Y} [\mathbb{E}[X|Y]]$$
이를 간단히 증명하면, $X$와 $Y$가 이산 확률변수라고 가정할 때 다음과 같습니다.
$$\begin{align} \mathbb{E}_{Y} [\mathbb{E}[X|Y]] &= \sum_{y} \left( \sum_{x} xp(X = x | Y = y) \right)p(Y = y) \\ &= \sum_{x, y} xp(X = x, Y = y) \\ &= \mathbb{E}[X] \end{align}$$
이를 보다 직관적으로 설명하기 위해 다음과 같은 예를 생각해 봅시다. 예를 들어, 확률변수 $X$ 는 전구의 수명을 나타내고 $Y$ 는 제조공장을 나타낸다고 할 때, 공장1의 전구는 평균 5000시간, 공장2는 평균 4000시간 지속된다고 하겠습니다. $p(Y = 1) = 0.6$ 그리고 $P(Y = 2) = 0.4$라고 가정하면 다음과 같이 두 공장에 대한 전구 수명의 기댓값을 알 수 있습니다.
$$\mathbb{E}[X] = \mathbb{E}[X|Y = 1]p(Y = 1) + \mathbb{E}[X|Y = 2]p(Y = 2) = 5000 \times 0.6 + 4000 \times 0.4 = 4600$$
분산에 대해서도 유사한 법칙이 있으며, 이를 전체 분산 법칙(law of total variance) 또는 조건부 분산 공식(conditional variance formula)이라고 부릅니다.
$$\mathbb{V}[X] = \mathbb{E}_{Y}[\mathbb{Y}[X|Y]] + \mathbb{V}_{Y} [\mathbb{E}[X|Y]]$$
이 공식은, 전체 분산이 각 조건부 분산의 평균과 조건부 기대값의 분산으로 구성된다는 것을 의미하며 증명과정은 다음과 같습니다. 먼저, 조건부 기대값 $\mu_{X | Y} = \mathbb{E}[X|Y]$, 조건부 2차 모멘트 $s_{X | Y} = \mathbb{E}[X^{2}|Y]$, 그리고 조건부 분산 $\sigma^{2}_{X | Y} = \mathbb{V}[X|Y] = s_{X|Y} - \mu^{2}_{X|Y}$를 정의합니다. 이 값들은 $Y$ 의 함수이기 때문에 역시 확률변수로 취급할 수 있습니다. 이를 바탕으로 전체 분산을 전개하면 다음과 같습니다.
$$\begin{align} \mathbb{V}[X] &= \mathbb{E}[X^{2}] - (\mathbb{E}[X])^{2} \\ &= \mathbb{E}_{Y} [s_{X|Y}] - \left( \mathbb{E}_{Y} [\mu_{X|Y}] \right)^{2} \\ &= \mathbb{E}_{Y} \left[ \sigma^{2}_{X|Y} \right] + \mathbb{E}_{Y} \left[ \mu^{2}_{X|Y} \right] - \left( \mathbb{E}_{Y} \left[ \mu_{X|Y} \right] \right)^{2} \\ &= \mathbb{E}_{Y}[\mathbb{V}[X|Y]] + \mathbb{V}_{Y}[\mu_{X|Y}]\end{align}$$
이 공식을 직관적으로 이해하기 위해 단변량 가우시안 혼합 모델(mixture of Gaussians)을 예로 들어봅시다. 확률변수 $X$ 가 평균이 다른 $K$ 개의 가우시안 혼합 성분 중 하나에서 생성된다고 가정하고, $Y$ 는 그 중 어떤 성분에서 생성되었는지를 나타내는 숨겨진 변수(hidden indicator variable)입니다. 여기서 $X = \sum_{y = 1}^{K} \pi_{y} \mathcal{N}(X|\mu_{y}, \sigma_{y})$라고 정의하겠습니다.
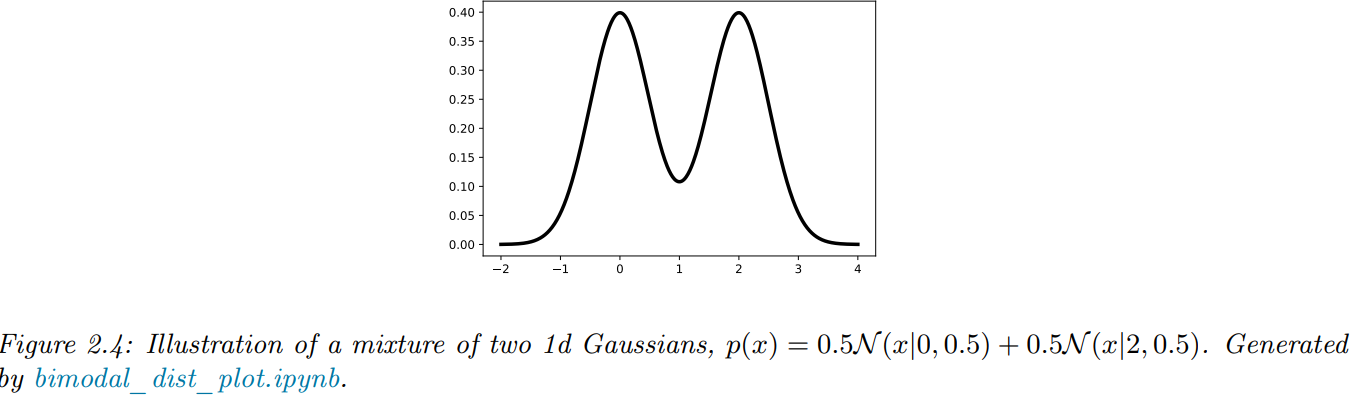
그러면 그림 2.4에서 보이는 것과 같이 $\pi_{1} = \pi_{2} = 0.5$ 그리고 평균 $\mu_{1} = 0, \mu_{2} = 2$, 표준편차 $\sigma_{1} = \sigma_{2} = 0.5$라고 하면 전체분산은 다음과 같이 구할 수 있습니다.
- 조건부분산의 평균: $\mathbb{E}[\mathbb{V}[X|Y]] = \pi_{1}\sigma^{2}_{1} + \pi_{2}\sigma^{2}_{2} = 0.25$
- 조건부기대값의 분산: $\mathbb{V}[\mathbb{E}[X|Y]] = \pi_{1} (\mu_{1} - \bar{\mu})^{2} + \pi_{2}(\mu_{2} - \bar{\mu}) = 1$
즉, 여기서 전체 분산의 대부분은 각 혼합 성분의 중심값들 간의 차이에서 발생하며, 각 성분 내의 국지적 분산(local variance)은 상대적으로 작은 역할을 함을 알 수 있습니다.
2.7 요약 통계량의 한계 (Limitations of summary statistics)

확률분포(혹은 분포에서 추출된 샘플들)를 평균과 분산과 같은 간단한 통계량으로 요약하는 것은 흔한 방법입니다. 하지만 이 과정에서 상당한 양의 정보가 손실될 수 있습니다. 이 현상을 극적으로 보여주는 대표적인 예시가 앤스콤의 4중주(Anscombe’s Quartet) 입니다. 그림 2.5에 나타난 이 예시는 4개의 서로 다른 데이터셋이 동일한 평균, 분산 및 상관계수 $\rho$ 값을 가지면서도 시각적으로 완전히 다른 패턴을 보이고 있습니다.
구체적으로 이 데이터셋들의 공통된 통계량은 다음과 같습니다. 평균은 $\mathbb{E}[x] = 9, \mathbb{E}[y] = 7.5$, 분산은 $\mathbb{V}[x] = 11, \mathbb{V}[y] = 4.12$, 그리고 상관계수는 $\rho = 0.816$입니다. 하지만 그림에서 명확히 보이듯, 각 데이터셋의 결합분포 $p(x, y)$ 는 완전히 다른 형태를 띠고 있습니다. 앤스콤은 각기 10개의 데이터 포인트로 이루어진 이 데이터셋들을 만들어, 통계학자들이 흔히 수치적인 요약 통계가 시각화보다 우월하다고 생각하는 경향을 지적했습니다.

이보다 더욱 흥미로운 예시는 그림 2.6에 나타난 Datasaurus Dozen 이라고 불리는 데이터셋입니다. 여기에는 공룡 모양의 데이터셋과 더불어, 서로 모양이 매우 다른 11개의 데이터셋이 포함되어 있습니다. 이 데이터셋들은 모두 낮은 차수(low-order)의 요약 통계량이 완전히 같습니다. 이 데이터셋들은 수치적 최적화 기법의 일종인 시뮬레이티드 어닐링(simulated annealing)을 이용하여 만들어졌으며, 목표 통계량에 대한 편차와 목표로 하는 특정 형태와의 거리를 최소화하도록 최적화되어 있습니다.

이와 같은 시뮬레이티드 어닐링 접근법은 1차원 데이터셋에도 적용할 수 있습니다(그림 2.7). 이 그림에서도 각 데이터셋은 뚜렷이 다른 형태를 보이지만, 중앙값(median)과 사분위 범위(inter-quartile range, IQR)는 모두 동일합니다. 중앙에 그려진 박스 플롯(Box plot)의 음영 부분이 이 사실을 나타냅니다.
이러한 정보 손실을 최소화하기 위해 사용되는 더 효과적인 시각화 방법이 바로 바이올린 플롯(Violin plot) 입니다(그림 2.7 우측). 바이올린 플롯은 데이터 분포의 밀도를 보다 직관적으로 나타내기 위해 커널 밀도 추정(kernel density estimation)을 이용하여 데이터의 밀도를 수직 축에 양쪽으로 그립니다(자세한 내용은 16.3절 참고). 또한 중앙값과 IQR도 함께 표시됩니다. 이 방법을 사용하면 분포 간 미묘한 차이를 시각적으로 더 잘 구별할 수 있지만, 이 방법은 1차원 데이터에만 적용할 수 있다는 제한이 있습니다.
