1. 베이즈 추론(Bayesian inference)
Bayes’s theorem is to the theory of probability what Pythagoras’s theorem is to geometry. — Sir Harold Jeffreys, 1973
위 문구에서도 알 수 있다싶이 확률론에서 베이즈 이론의 중요성을 매우 크게 강조하고 있습니다. 기하학의 대표적인 정리가 피타고라스 정리라면 확률론의 대표적인 정리는 베이즈 이론이죠. 오늘은 본격적으로 베이즈 추론(Bayesian inference)의 기초에 대해 살펴보겠습니다. 우선 ‘추론(inference)’이라는 말은 사전적으로는 "표본 데이터를 바탕으로 일반적인 결론으로 나아가는 행위로, 일반적으로 확신의 정도를 계산하여 진행하는 것"을 뜻합니다. 그리고 ‘베이즈적(Bayesian)’이라는 표현은 확률 이론을 이용해 이러한 "확신의 정도"를 표현하고, 관측 데이터를 바탕으로 업데이트할 때 베이즈 규칙을 활용하는 방식을 의미합니다.
베이즈 규칙은 매우 간단합니다. 이는 단지 "관측된 데이터 $Y = y$ 가 있을 때, 아직 알 수 없는(숨겨진) 변수 $H$가 특정 값 $h$ 를 가질 확률"을 계산하는 공식입니다. 수식으로 나타내면 다음과 같습니다.
$$p(H = h | Y = y) = \frac{p(H = h)p(Y = y | H = h)}{p(Y = y)}$$
이 식은 다음과 같은 기본적인 확률의 곱 규칙(product rule)으로부터 바로 유도할 수 있습니다.
$$p(h|y)p(y) = p(h)p(y|h) = p(h, y)$$
이 수식에서 등장하는 각 항의 의미를 하나씩 살펴보겠습니다.
- 사전 확률 (Prior distribution, $p(H)$): 이는 데이터를 관찰하기 전에 우리가 가지고 있던 숨겨진 변수 $H$ 에 대한 지식 또는 믿음입니다. 예를 들어, $H$ 가 가질 수 있는 값이 $K$ 개라면, 사전 확률 $p(H)$ 는 이들 값에 대응하는 $K$ 개의 확률을 갖는 벡터이며, 그 합이 1이 됩니다.
- 관측 확률 분포 (Observation distribution, $p(Y|H=h)$): 이는 특정 값 $h$ 일 때 관측 가능한 결과 $Y$ 의 확률적 분포를 나타냅니다. 우리가 실제 관찰한 데이터를 $y$ 라 하면, 이 값을 $h$마다 계산한 함수인 $p(Y = y|H = h)$를 우도(likelihood) 라고 불립니다. (단, 이 값은 $h$ 에 대한 함수이지만, 모든 $h$ 에 대해 합이 1이 되는 확률 분포는 아닙니니다.)
사전 확률과 우도를 곱하면, 각 $h$ 에 대해 정규화되지 않은 결합 분포(unnormalized joint distribution) $p(H = h, Y = y)$ 를 얻습니다. 이 정규화되지 않은 결합 분포를 확률 분포로 만들기 위해서는 분모인 주변 우도(marginal likelihood, $p(Y = y)$ )로 나눠주어야 합니다. 이 주변 우도는 숨겨진 변수 $H$의 모든 가능한 값에 대해 결합 분포를 더한 값으로 다음과 같이 계산됩니다.
$$P(Y = y) = \sum_{h^{'} \in \mathcal{H}} p(H = h^{'})p(Y = y|H=h^{'}) = \sum_{h^{'} \in \mathcal{H}} p(H=h^{'}, Y=y)$$
최종적으로 결합 분포를 주변 우도로 나눠 정규화하면, 우리가 관심 있는 사후 확률 분포(posterior distribution, $p(H = h | Y = y)$ )를 얻게 됩니다. 이 사후 확률 분포는 데이터를 관찰한 뒤 숨겨진 변수 $H$ 의 가능한 값에 대한 우리의 업데이트된 믿음입니다. 이러한 베이즈 규칙은 다음과 같이 간략히 표현할 수 있습니다.
$$\text{posterior} \propto \text{prior} \times \text{likelihood}$$
여기서 $\propto$ 는 '비례한다'는 뜻으로 $p(Y = y)$ 는 변수 $H$ 와 상관없는 상수이므로 일단 생략해도 됩니다.
이처럼, 베이즈 규칙을 활용하여 관심 있는 어떤 변수에 대한 확률 분포를 데이터를 통해 갱신하는 방식을 베이즈 추론(Bayesian inference) 또는 사후 확률 추론(posterior inference)이라고 부릅니다. 이를 단순히 확률적 추론(probabilistic inference)이라고도 합니다.
2. 베이즈 규칙의 예시
다음에는 간단한 사례를 통해 베이즈 추론이 실제 어떻게 적용되는지 살펴보도록 하겠습니다.
2.1 COVID-19 검사 결과 해석하기
COVID-19(코로나바이러스 감염증-19)는 SARS-CoV-2 바이러스로 인해 발생하는 전염병입니다. 여러분이 혹시 코로나19에 감염됐다고 생각해 봅시다. 감염 여부를 확인하기 위해 진단 검사를 받고, 이 검사 결과를 통해 자신이 실제 감염되었는지 여부를 확인하고 싶다고 가정하겠습니다.
먼저 상황을 수학적으로 간단하게 표현해 보겠습니다. $H = 1$과 $H = 0$은 실제로 감염된 경우와 아닌경우, 그리고 $Y = 1$과 $Y = 0$은 검사 결과가 양성인 경우와 음성인 경우로 정하겠습니다. 이 상황에서 우리가 구하고자 하는 값은 검사 결과 $Y = y$가 관측되었을 때 실제 감염 여부 $H = h$의 확률입니다. 즉, 우리는 $p(H = h|Y = y)$를 계산해야하죠. 편의를 위해 간단히 확률 분포를 $p(H|y) = [p(H = 0|Y = y), p(H = 1|Y = y)]$라고 표기할 수 있습니다. 이것은 실제 감염 여부를 예측하는 일종의 이진 분류(binary classification) 문제로 볼 수도 있습니다. 여기서, $H$는 우리가 모르는 클래스(감염 여부)이며 $y$ 는 진단 검사를 통해 얻은 데이터입니다.
2.1.1 검사 정확도 이해하기
검사 결과의 신뢰도를 평가하기 위해 민감도(Sensitivity, 참 양성률)와 특이도(Specificity, 참 음성률)라는 중요한 개념이 있습니다.
- 민감도(Sensitivity, 참 양성률) $p(Y = 1|H = 1)$: 실제로 감염된 사람이 양성 결과를 받을 확률입니다.
- 특이도(Specificity, 참 음성률) $p(Y = 0|H = 0)$: 실제로 감염되지 않은 사람이 음성 결과를 받을 확률입니다.
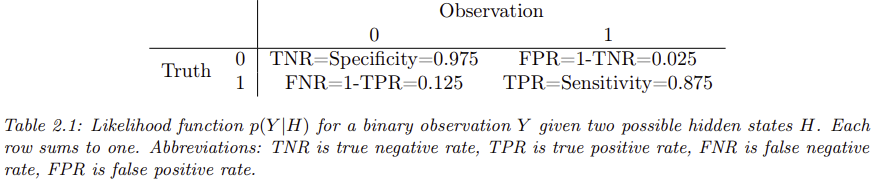
여기서 거짓 음성률(False Negative Rate)는 민감도의 반대 개념으로, 실제 감염된 사람이 음성 결과를 받을 확률입니다. 그리고 거짓 양성률(False Positive Rate)은 특이도의 반대 개념으로, 실제 감염되지 않은 사람이 양성 결과를 받을 확률입니다. 실제 데이터를 참고하여 민감도는 87.5%, 특이도는 97.5%로 설정해 보겠습니다. (표 2.1 참고)
2.1.2 사전 확률(Prevalence)
감염 여부의 확률을 계산하려면 검사 전, 지역 내 질병의 실제 유병률(prevalence)을 알아야 합니다. 이 값을 사전 확률(prior)이라고 합니다. 2020년 봄 뉴욕시의 코로나19 유병률이 약 10%였다고 하므로, 이를 사전 확률로 설정하면 $p(H = 1) = 0.1$ 이고 $p(H = 0) = 0.9$입니다.
2.1.3 검사 결과가 양성일 때 감염 확률 계산
이제 실제로 검사를 받았는데 결과가 양성($Y = 1$) 이라고 가정합시다. 이때 실제 감염될 확률을 베이즈 규칙으로 계산하면 다음과 같습니다.
$$\begin{align} p(H = 1 | Y = 1) &= \frac{p(Y = 1|H = 1)p(H = 1)}{p(Y = 1|H=1)p(H=1) + p(Y=1)p(H=0)p(H=0)} \\ &= \frac{0.875 \times 0.1}{0.875 \times 0.1 + 0.025 \times 0.9} = 0.795 \end{align}$$
즉, 양성 결과를 받았을 때 실제 감염 확률은 약 79.5%입니다.
2.1.4 검사 결과가 음성일 때 감염 확률 계산
이번에는 실제로 검사를 받았는데 결과가 성($Y = 0$) 이라고 가정합시다. 이때 실제 감염될 확률을 베이즈 규칙으로 계산하면 다음과 같습니다.
$$\begin{align} p(H = 1 | Y = 0) &= \frac{p(Y = 0|H = 1)p(H = 1)}{p(Y = 0|H=1)p(H=1) + p(Y=0)p(H=0)p(H=0)} \\ &= \frac{0.125 \times 0.1}{0.125 \times 0.1 + 0.975 \times 0.9} = 0.014 \end{align}$$
즉, 음성 결과를 받았을 때 실제 감염 확률은 약 1.4%입니다.
2.1.5 유병률이 낮아졌을 때의 상황
이번에는 COVID-19의 유병률이 매우 낮아졌다고 가정합시다. 만약 유병률이 1%로 낮아졌다면, 위의 계산을 다시 하면 양성일 때 감염확률은 26% 그리고 음성일 때 감염확률은 0.13%가 됩니다.
유병률이 낮을 때는 검사 결과가 양성이라도 실제 감염 확률이 생각보다 낮게 나옵니다. 이는 매우 직관에 어긋나는 결과입니다. 이유는 질병 자체가 희소한 경우, 한 번의 양성 결과는 실제 감염보다는 오히려 잘못된 양성(False Positive)일 가능성이 높기 때문입니다.
예를 들어, 10만 명 중 1000명만 감염된 상황에서, 감염된 1000명 중 875명이 양성으로 나타나고, 감염되지 않은 99,000명 중 2475명이 양성으로 잘못 나타나게 됩니다. 전체 양성은 875 + 2475 = 3350명이므로, 이 중 실제 감염자는 875명으로 전체 양성자 대비 실제 감염 비율은 875/3350 ≈ 26%밖에 되지 않습니다.
2.2 몬티 홀(Monty Hall) 문제
이번에는 베이즈 규칙을 활용한 재미있는 예시 하나를 살펴보겠습니다. 바로 유명한 몬티 홀(Monty Hall) 문제입니다. 이 문제는 개인적으로 제가 제일 좋아하는 확률론 문제 중 하나입니다.
2.2.1 몬티 홀 문제의 규칙
게임쇼를 상상해 봅시다. 여기에는 1번, 2번, 3번의 문이 있고, 이 중 하나의 문 뒤에는 자동차와 같은 큰 상품이 숨겨져 있습니다. 여러분은 먼저 이 중 하나의 문을 선택합니다. 여러분이 문을 선택한 후, 진행자는 여러분이 고르지 않은 나머지 두 문 중 하나를 엽니다. 물론, 진행자는 상품이 숨겨진 문은 절대 열지 않고, 항상 빈 문을 열어서 보여줍니다. 이때 진행자가 빈 문을 하나 열어준 뒤, 여러분에게 새로운 선택의 기회가 주어집니다.
- 원래 선택한 문을 그대로 유지할 수도 있고,
- 아직 열리지 않은 다른 문으로 바꿀 수도 있습니다.
마지막으로 여러분이 선택한 문이 열리고, 그 문 뒤에 있는 상품을 얻게 됩니다.
예를 들어, 여러분이 처음에 1번 문을 골랐고, 진행자가 3번 문을 열어 아무것도 없음을 보여줬다고 생각해 봅시다. 이때 여러분은 다음 중 어떤 결정을 내리는 게 좋을까요?
- (a) 처음 선택한 1번 문을 유지한다.
- (b) 아직 열리지 않은 2번 문으로 바꾼다.
- (c) 바꾸든 바꾸지 않든 차이가 없다.
2.2.2 직관적 오해와 실제 결과
직관적으로는 처음 선택한 문이 상품의 위치에 영향을 주지 않을 것 같기 때문에 바꾸거나 유지하거나 아무 차이가 없어 보입니다. 하지만 실제로는 진행자가 3번 문을 열었다는 사실이 상품 위치에 대한 중요한 정보를 주고 있습니다. 진행자는 상품의 위치와 여러분의 최초 선택을 모두 알고 난 뒤 빈 문을 골랐기 때문입니다. 놀랍게도, 문을 바꾸는 것이 상품을 얻을 확률을 두 배나 높입니다.
2.2.3 베이즈 규칙으로 분석하기
이를 명확하게 이해하기 위해 베이즈 규칙을 이용하여 분석해 보겠습니다. 먼저, $H_{i}$를 "상품이 $i$번 문 뒤에 있다" 는 가설이라고 합시다. 상품이 어떤 문 뒤에 있을 확률은 게임이 시작되기 전에는 모두 동일하다고 가정합니다. 즉, 다음과 같이 동일한 사전 확률을 가정합니다.
$$P(H_{1}) = P(H_{2}) = P(H_{3}) = \frac{1}{3}$$
이제 여러분이 1번 문을 골랐다고 가정해 봅시다. 이때 진행자가 여는 문(관측 데이터)은 $Y$ 이며, 이때 $Y = 2$ 는 2번 문이 열렸다는 의미이고, $Y = 3$ 은 3번 문이 열렸다는 의미입니다. 이를 통해 진행자의 행동 확률은 다음과 같이 정리할 수 있습니다:
- 만약 상품이 1번 문 뒤에 있다면, 진행자는 2번 또는 3번 중 하나를 랜덤으로 열 것입니다.
- 상품이 다른 문 뒤에 있다면, 진행자는 상품이 숨겨져 있지 않은 문만 열 수 있습니다.
따라서 조건부 확률은 다음과 같습니다.

2.2.4 실제 계산 예시
여러분이 1번 문을 골랐고 진행자가 3번 문을 열었을 때 ($Y = 3$) , 각 문 뒤에 상품이 있을 확률을 베이즈 규칙을 이용해 계산해 보겠습니다. 베이즈 규칙은 다음과 같습니다.
$$P(H_{i} | Y = 3) = \frac{P(Y = 3|H_{i})P(H_{i})}{P(Y = 3)}$$
이를 각 경우에 대입하면,
$$P(H_{1} | Y = 3) = \frac{P(Y = 3|H_{1})P(H_{1})}{P(Y = 3)} = \frac{\frac{1}{2} \times \frac{1}{3}}{P(Y = 3)}$$
$$P(H_{2} | Y = 3) = \frac{P(Y = 3|H_{2})P(H_{2})}{P(Y = 3)} = \frac{1 \times \frac{1}{3}}{P(Y = 3)}$$
$$P(H_{3} | Y = 3) = \frac{P(Y = 3|H_{3})P(H_{3})}{P(Y = 3)} = \frac{0 \times \frac{1}{3}}{P(Y = 3)}$$
여기서 분모 $P(Y = 3)$ 는 모든 가능한 $H$값에 대한 합이므로
$$\begin{align} P(Y = 3) &= P(Y = 3|H_{1})P(H_{1}) + P(Y = 3|H_{2}) + P(Y=3|H_{3})P(H_{3}) \\ &= \frac{1}{2} \cdot \frac{1}{3} + 1 \cdot \frac{1}{3} + 0 \cdot \frac{1}{3} = \frac{1}{2} \end{align}$$
이 결과를 이용하면, 사후 확률은 다음과 같습니다.
$$P(H_{1} | Y = 3) = \frac{1}{3}$$
$$P(H_{2} | Y = 3) = \frac{2}{3}$$
$$P(H_{3} | Y = 3) = 0$$
즉, 상품이 2번 문 뒤에 있을 확률이 2/3(약 66.7%)로 가장 높습니다. 따라서 여러분은 최초에 선택한 문(1번 문)에서 다른 문(2번 문)으로 바꾸는 것이 상품을 얻을 가능성을 두 배로 높입니다.
2.2.5 직관적으로 이해하기 쉬운 확장 예시
많은 사람이 위 결과를 듣고도 놀라워하거나 잘 이해하지 못합니다. 이런 경우 이해하기 쉬운 직관적 예시를 생각해 볼 수 있습니다.
예를 들어, 문이 100만 개 있고 여러분이 그 중 하나(예를 들어 1번 문)를 선택했다고 생각합시다. 그 뒤 진행자는 999,998개의 문을 열고 오직 두 개의 문(여러분이 고른 1번 문과 다른 한 개의 문 예: 234,598번 문)만 남겨둔다면, 여러분은 선택을 바꾸시겠습니까? 이 경우, 처음 여러분이 아무 정보 없이 고른 문에 상품이 있을 확률이 매우 낮기 때문에, 남은 다른 문으로 선택을 바꾸는 게 훨씬 이득이라는 것을 쉽게 직관할 수 있습니다.
이처럼 몬티 홀 문제는 베이즈 규칙을 이용한 확률적 추론이 직관적인 사고와 다를 수 있음을 보여주는 흥미로운 예시입니다.
3. 역문제(Incerse Problem)
확률 이론(probability theory)은 세상의 상태(state of the world), 즉 숨겨진 변수 $h$를 알고 있을 때, 그로부터 나올 결과 $y$의 확률 분포를 예측하는 데 관심이 있습니다. 반면 역확률(inverse probability)은 관찰된 결과로부터 세상의 상태를 추론하는 데 관심이 있습니다. 다시 말해, 이미 발생한 결과 $y$ 를 관찰한 뒤, 이것을 유발한 숨겨진 원인 $h$ 를 추론하는 것입니다. 이를 쉽게 표현하면, 다음과 같은 역방향의 문제를 푸는 것이라 할 수 있습니다.
$$h \rightarrow y \Rightarrow y \rightarrow h$$
3.1 역문제의 예시와 근본적 한계

예를 들어, 그림 2.8과 같이 하나의 2차원 이미지 $y$ 로부터 그것이 나타내는 3차원 물체의 형태 $h$ 를 추론하는 문제를 생각해 봅시다. 이는 컴퓨터 비전 분야에서 매우 중요한 고전적 문제이기도 합니다.
그런데 이 문제는 근본적으로 ‘부정확한(ill-posed)’ 문제입니다. 즉, 하나의 2차원 이미지로부터 정확한 3차원 모양을 복원할 수 없는 이유는, 여러 개의 서로 다른 3차원 형태 $h$ 가 동일한 2차원 이미지 $y$ 를 만들어 낼 수 있기 때문입니다.
또 다른 예로 자연어 이해(Natural Language Understanding) 문제를 들 수 있습니다. 듣는 사람이 말하는 사람이 사용하는 단어 $y$ 로부터 화자의 진짜 의도 $h$ 를 정확히 추론해야 하는 문제 역시 역문제이며, 이 또한 근본적으로 모호성을 포함하는 부정확한 문제입니다.
3.2 역문제를 해결하기 위한 베이즈 규칙의 활용
이처럼 불명확한 역문제를 다루기 위해서는, 베이즈 규칙을 활용하여 숨겨진 상태에 대한 사후 확률 $p(h|y)$ 를 계산할 수 있습니다. 이때, 베이즈 규칙을 사용하려면 다음 두 가지가 필요합니다.
- 순방향 모델(forward model): $p(y|h)$, 즉 숨겨진 상태 $h$에서 어떻게 관측 데이터 $y$가 생성되는지를 모델링한 것.
- 사전 확률(prior): $p(h)$, 즉 세상에 존재할 수 있는 상태들의 초기 확률을 나타내는 것으로, 불가능하거나 그럴듯하지 않은 상태의 가능성을 낮추는 역할을 합니다.
이 두 가지를 통해 관측 데이터로부터 세상의 상태에 대한 믿음의 분포(posterior distribution)를 얻을 수 있으며, 이는 다양한 역문제를 해결하는 데 중요한 역할을 합니다. 역문제 해결 방법과 베이즈적 접근에 대한 보다 깊은 내용은 향후에 더 자세히 다루도록 하겠습니다.
