안녕하세요. 지난 포스팅의 [IC2D] Drop an Octave: Replacing Spatial Redundancy in Convolutional Neural Networks with Octave Convolution (ICCV2019)에서는 저주파에 존재하는 Spatial Redundancy를 줄일 수 있는 OctConv에 대한 이야기를 해드렸습니다. 오늘도 CNN 구조에 큰 영향을 주었던 Selective Kernel Networks에 대해서 소개시켜드리겠습니다.
Selective Kernel Networks
In standard Convolutional Neural Networks (CNNs), the receptive fields of artificial neurons in each layer are designed to share the same size. It is well-known in the neuroscience community that the receptive field size of visual cortical neurons are modu
arxiv.org
Background
본 논문의 기본적인 motivation은 CNN 설계의 기본 원리인 고양이 눈에 존재하는 Local Receptive Field (RF)입니다. 이러한, Local RF의 가장 큰 특징은 동일한 위치의 뉴런의 RF에 따라서도 크기가 가지각색이라는 점 입니다. 이를 통해, 고양이는 다양한 크기의 사물을 인지할 수 있게 되는 것이죠. 이러한 구조를 활용한 대표적인 모델이 바로 multi-branch 모델인 InceptionNet입니다.
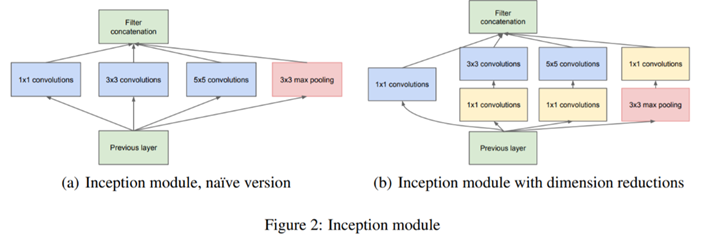
InceptionNet은 실제로 정말 많은 변형들이 제안되어 현재까지 multi-branch 모델의 근본 구조가 되었습니다. 이를 통해, 고양이의 눈과 같이 다양한 크기의 객체를 인지할 수 있는 능력을 가지게 되었다고 합니다.
하지만, 많은 딥 러닝 연구자들이 간과하고 있는 RF의 두번째 특성이 있다고 합니다. 바로 RF의 크기가 이전 뉴런의 자극에 따라 적응적으로 (Adaptively) 크기가 변화한다는 점입니다. 본 논문에서는 간과된 RF의 특성을 CNN 구조에 넣기 위해 Selective Kernel Networks를 제안합니다.
- 기본적으로 InceptionNet은 multi-branch를 가지더라도 각각의 branch가 가지는 중요도는 동일하다고 가정하기 때문에 단순한 선형적인 aggregation을 수행합니다.
- Selective Kernel (SK) 합성곱 연산은 크게 Split, Fuse, Select의 연산으로 나누어집니다.
- SK 합성곱 연산은 파라미터의 개수가 적은 lightweight 연산으로 계산 복잡도 역시 낮습니다.
- SK 합성곱 연산은 기존 ResNext에 추가하여 학습했을 때 ImageNet2012, CIFAR10, CIFAR100에서 SOTA 성능을 달성하였습니다.
Method
1). Selective Kernel Convolution
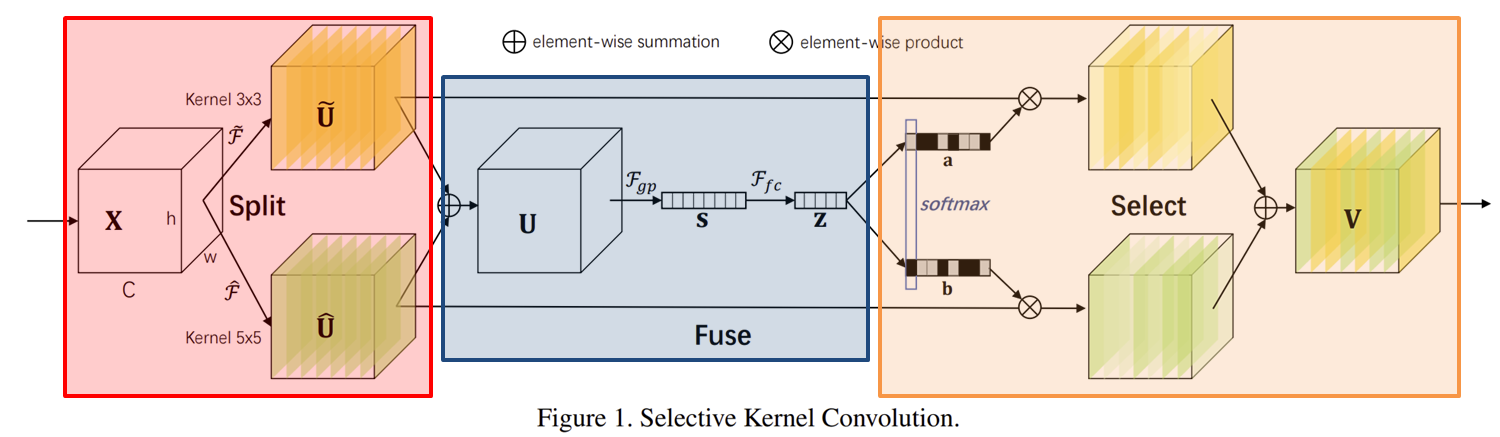
Background에서 설명드렸다싶이 SK 합성곱은 그림1과 같이 3개의 연산인 Split, Fuse, Select로 구성되어 있습니다. 이번 절에서는 각 연산이 수행되는 방식에 대해서 말씀드리도록 하겠습니다.
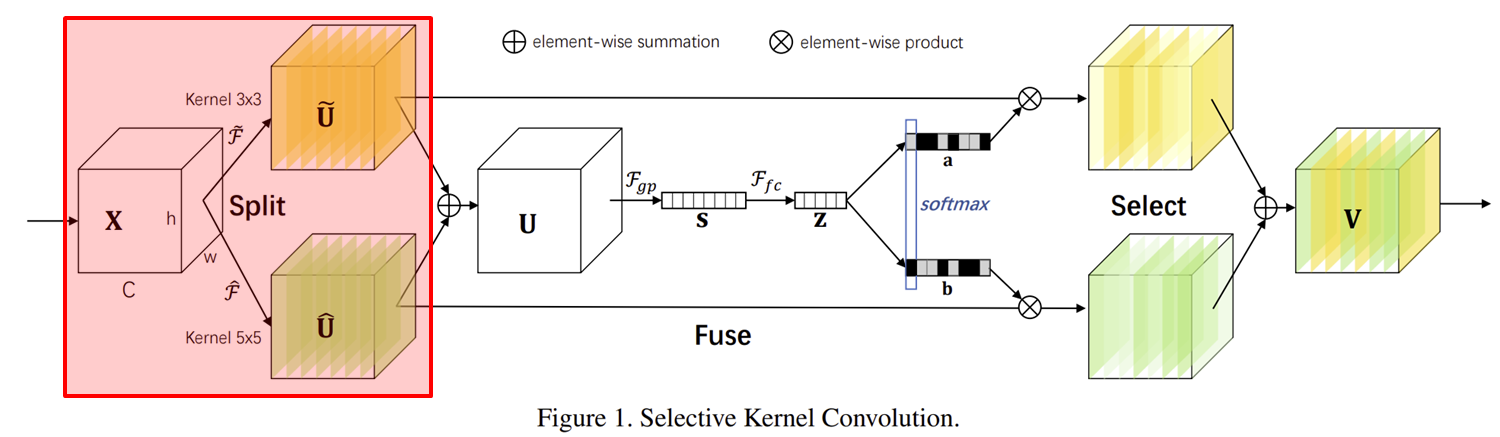
먼저, 빨간색으로 칠해진 Split 연산입니다. 이름에서도 보이다싶이 입력 특징 맵 $\mathbf{X} \in \mathbb{R}^{h \times w \times C}$를 서로 다른 커널의 크기를 가지는 $M$개의 연산을 각각 적용하게 됩니다. 이 부분까지는 InceptionNet과 어느정도 유사한 거 같습니다. 그림1에서는 단순하게 그리기 위해 $M = 2$로 설정하였으며 두 개의 커널 크기인 $3 \times 3$과 $5 \times 5$를 가지는 두 연산 $\tilde{F}$와 $\hat{F}$를 적용합니다. 이때, 두 연산 모두 합성곱 연산을 수행한 뒤 배치 정규화와 ReLU 활성화 함수로 구성되어 있습니다. 이때, 더욱 효율적인 연산을 위해 $5 \times 5$ 크기의 합성곱 연산을 $3 \times 3$ 크기의 합성곱으로 dilation을 2로 설정하여 수행할 수도 있습니다. 이 경우 역시 receptive field는 $5 \times 5$와 동일하지만 파라미터의 개수는 $9 / 25 \approx 0.36$배 더 감소하기 때문에 굉장히 효율적임을 알 수 있습니다.
이를 다음과 같이 수학적으로 표현할 수 있습니다. 단, $M = 2$입니다.
$$\begin{cases} &\tilde{F}: \mathbf{X} \rightarrow \tilde{\mathbf{U}} \in \mathbb{R}^{H \times W \times C} \\ &\hat{F}: \mathbf{X} \rightarrow \hat{\mathbf{U}} \in \mathbb{R}^{H \times W \times C} \end{cases}$$
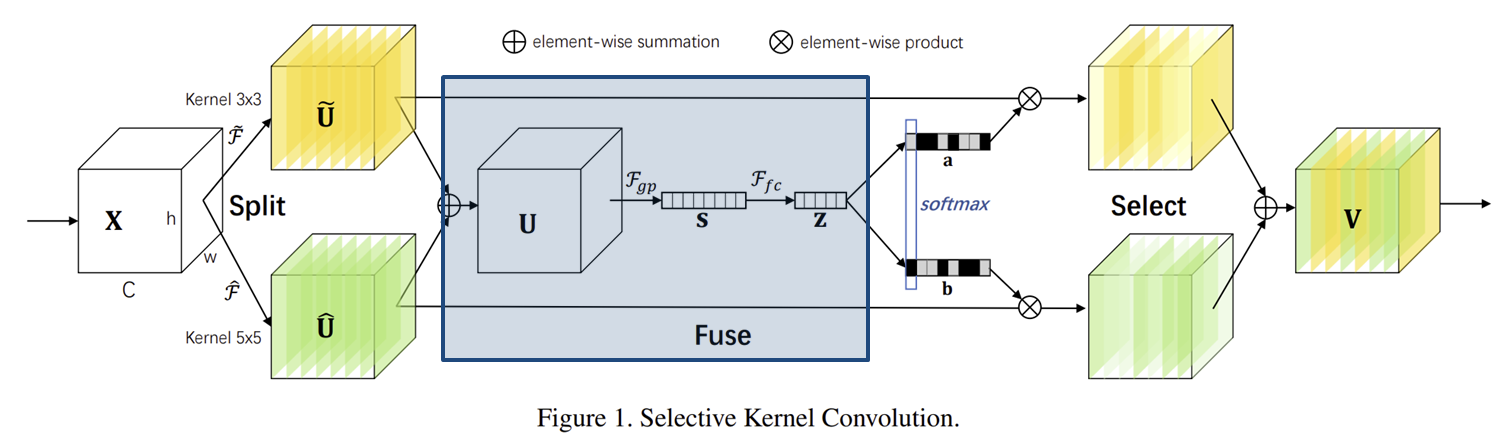
다음으로 파란색 영역인 Fuse 연산입니다. 딱 3개의 단계로 이루어진 연산입니다. 먼저, 서로 다른 $M$개의 연산을 적용한 뒤 하나로 summation을 수행합니다.
$$\mathbf{U} = \tilde{\mathbf{U}} + \hat{\mathbf{U}} \in \mathbb{R}^{H \times W \times C}$$
다음으로 Global Average Pooling을 통해 채널 설명자 (channel descriptor) $\mathbf{s} \in \mathbb{R}^{C}$로 $\mathbf{U}$를 임베딩합니다.
$$\mathbf{s}_{c} = \mathcal{F}_{gp} (\mathbf{U}_{c}) = \frac{1}{H \times W} \sum_{i = 1}^{H} \sum_{j = 1}^{W} \mathbf{U}_{c} (i, j)$$
마지막으로 채널 설명자 $\mathbf{s}$를 더 작은 차원을 가지는 $\mathbf{z} \in \mathbb{R}^{d}$로 압축합니다.
$$\mathbf{z} = \mathcal{F}_{fc} (\mathbf{s}) = \delta (\mathcal{B} (\mathbf{W} \mathbf{s})) \in \mathbb{R}^{d}$$
여기서, $\mathbf{W} \in \mathbb{R}^{d \times C}$로 학습가능한 파라미터, $\mathcal{B}$와 $\delta$는 각각 배치 정규화 및 ReLU 함수를 의미합니다. 전체적인 Fuse 연산을 보시면 SE Block과 어느정도 유사한 면이 있습니다. 그래서 그런지 실제로 reduce ratio 파라미터인 $r$을 도입하였습니다. 그래서 감소된 차원 $d$에 따른 성능 분석을 위해 다음과 같이 정의합니다.
$$d = \text{max} (C / r, L)$$
여기서 $L = 32$로 reduce ratio $r$을 통해 줄일 수 있는 최대 차원입니다. 즉, 아무리 줄여도 32개의 채널보다는 많거나 같다는 뜻이죠.

마지막 연산은 압축된 채널 설명자 $\mathbf{z} \in \mathbb{R}^{d}$를 기반으로 $M$개의 branch의 특징 맵의 채널에 attention을 적용합니다. 이 과정에서 $\mathbf{z}$의 채널 개수는 $d$개이고 각 branch의 채널 개수는 $C$개이기 때문에 shape 변경을 위한 $\mathbf{A}_{C} \in \mathbb{R}^{C \times d}$와 $\mathbf{B}_{C} \in \mathbb{R}^{C \times d}$를 각각 적용해줍니다. 그러면 $C$개의 채널을 가지는 두 채널 설명자 $\mathbf{a}$와 $\mathbf{b}$를 얻을 수 있습니다. 여기서 중요한 것은 $M$개의 branch간 가지고 있는 서로 다른 크기의 RF를 활용하겠다는 것 입니다. 따라서, $M$개의 branch에 대해서 각각 softmax를 수행해줍니다.
$$\begin{cases} &\mathbf{a}_{c} &= \frac{e^{\mathbf{A}_{c} \mathbf{z}}}{e^{\mathbf{A}_{c} \mathbf{z}} + e^{\mathbf{B}_{c} \mathbf{z}}} \\ &\mathbf{b}_{c} &= \frac{e^{\mathbf{B}_{c} \mathbf{z}}}{e^{\mathbf{A}_{c} \mathbf{z}} + e^{\mathbf{B}_{c} \mathbf{z}}} \end{cases}$$
이제 추출된 채널 설명자와 각 branch를 곱한 뒤 하나로 summation해주면 SK 합성곱 연산이 종료됩니다.
$$\mathbf{V}_{c} = \mathbf{a}_{c} \cdot \tilde{\mathbf{U}_{c}} + \mathbf{b}_{c} \cdot \hat{\mathbf{U}_{c}}$$
2). Network Architecture
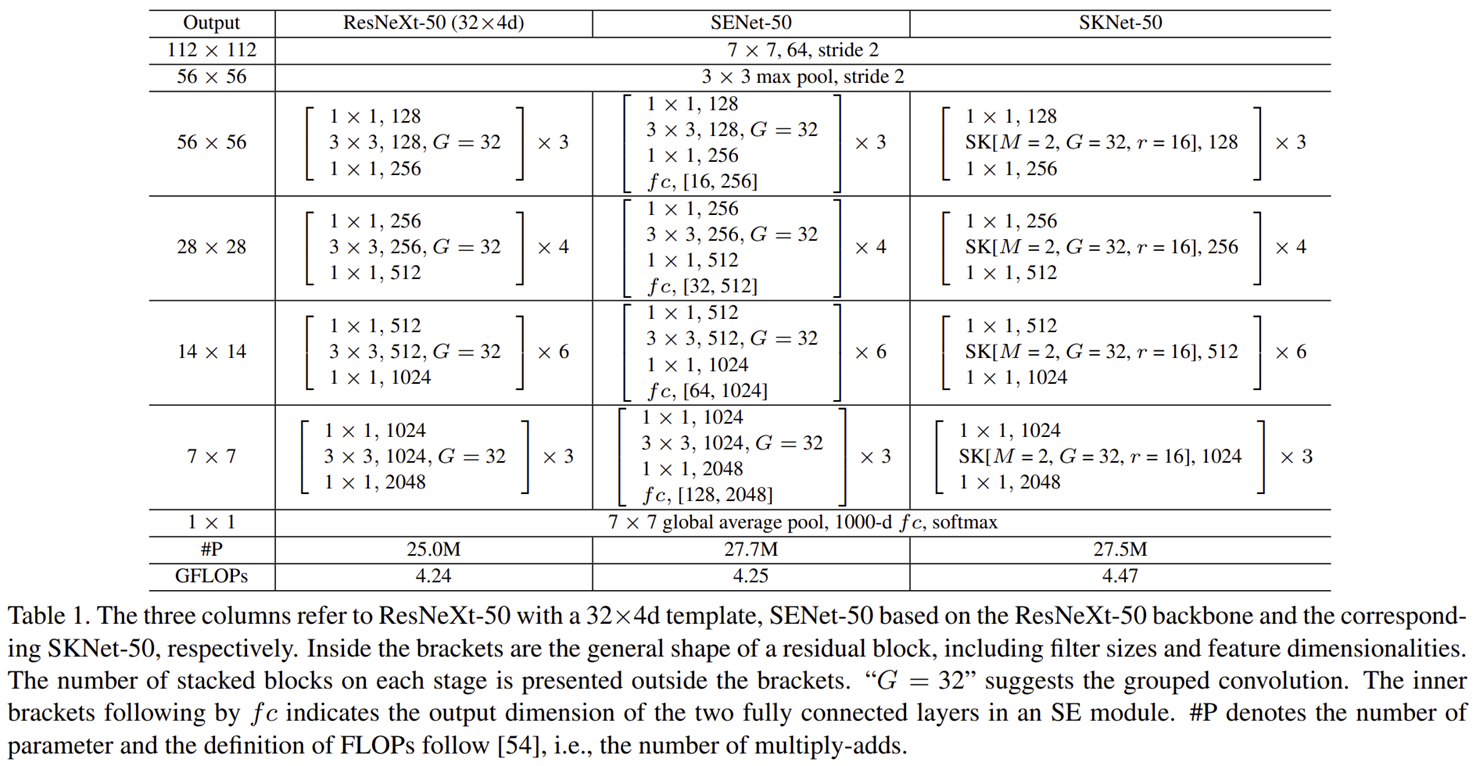
표1은 original ResNeXt-50와 SENet-50 그리고 SKNet-50을 정리한 것 입니다. 본 논문에서는 ResNeXt을 기본 베이스라인으로 잡은 이유를 2가지로 설명하고 있습니다. 1). 그룹 합성곱 연산 활용으로 적은 연산량, 2). ImageNet과 같은 이미지 인식 분야에서 SOTA 모델 인 점을 강조하고 있습니다. 이때, SK 합성곱 연산을 ResNeXt에 적용하기 위해 ResNet-like 모델에서 사용하는 Bottleneck 구조를 참고하여 새롭게 구현합니다. 즉, $1 \times 1$ 합성곱 연산, SK 합성곱 연산, 그리고 다시 $1 \times 1$ 합성곱 연산 순으로 연산을 적용하죠. 이를 본 논문에서는 "SK Unit"이라고 정의합니다. 이와 같이 모델을 구성하더라도 ResNeXt-50와 비교했을 때 파라미터 개수는 약 10%, 계산 복잡도는 5% 밖에 증가하지 않았다고 하네요.
또한, SKNet의 주요 하이퍼파라미터는 branch의 개수인 $M$, 그룹 합성곱 연산의 그룹 개수인 $G$ 그리고 reduction ratio $r$로 구성되어 있습니다. 그래서 단일 SK Unit을 하이퍼파라미터와 함께 표기하면 SK[$M$, $G$, $r$]이라고 쓸 수 있습니다. 그리고, ResNet에서 제안되었던 것과 마찬가지로 각 stage에서 사용하는 블록의 개수는 $\{3, 4, 6, 3\}$으로 동일합니다.
SK 합성곱 연산의 효율성은 ResNet-like 모델 뿐만 아니라 MobileNet 및 ShuffleNet과 같은 $3 \times 3$ 크기의 depthwise convolution을 활용하는 모델에서도 쉽게 적용할 수 있다고 합니다.
Experiment Results
본 논문에서는 ImageNet, CIFAR10, CIFAR100에서 영상 분류 실험을 수행하여 SOTA 성능을 달성하였습니다.
1). ImageNet Classification Results
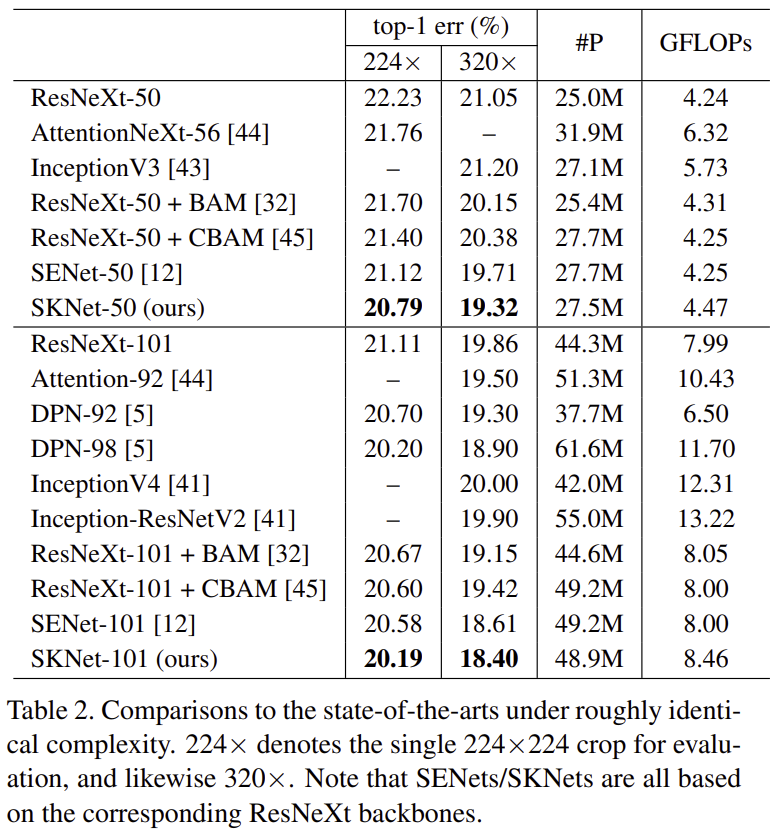
표2는 SK 합성곱을 ResNeXt에 적용했을 때 성능을보여주고 있습니다. 결과적으로 파라미터 개수 및 FLOPs에 비해 상대적으로 높은 성능을 보여주고 있습니다.
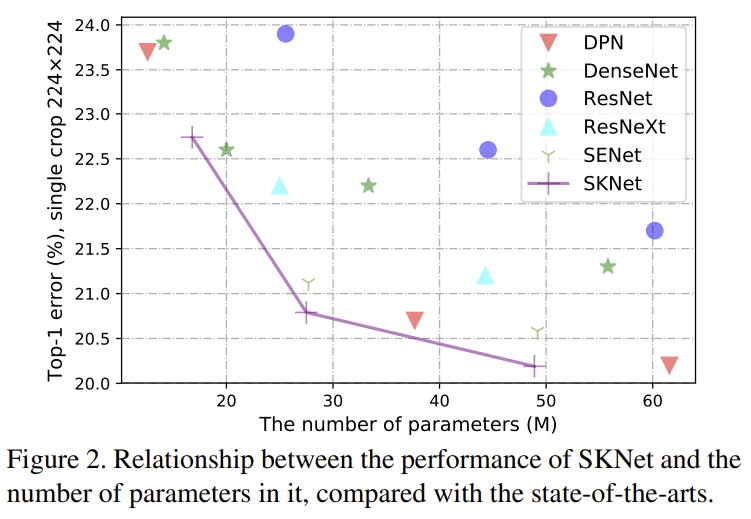
이를 파라미터 개수 vs Performance를 이용한 그래프를 그려보았을 때 동일 파라미터 개수에서 낮은 ImageNet Classification Error를 달성하고 있습니다.
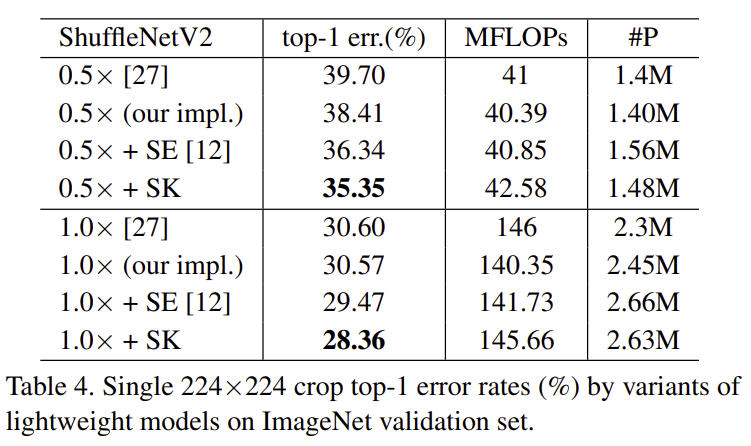
또한, ShuffleNetV2에 SK 합성곱 연산을 적용했을 때 성공적으로 성능 향상을 달성할 수 있었습니다.
2). CIFAR Classification Results
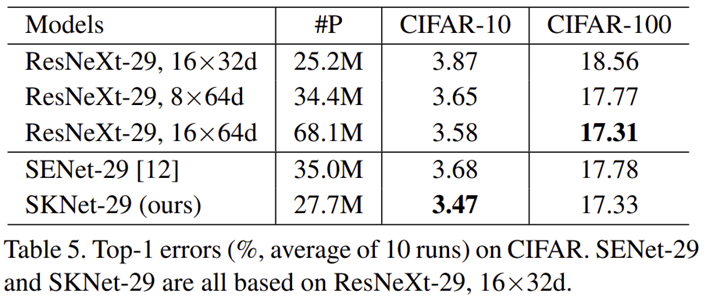
CIFAR에서도 마찬가지로 성능이 높은 것을 볼 수 있죠.
Implementation Code
import torch
import torch.nn as nn
class SKConv(nn.Module):
def __init__(self,
in_channels,
stride,
M=2, G=32, r=16, L=32):
super(SKConv, self).__init__()
self.in_channels = in_channels
self.M = M
d = max(int(in_channels / r), L)
self.conv_branches = nn.ModuleList([])
for i in range(M):
self.conv_branches.append(
nn.Sequential(nn.Conv2d(in_channels, in_channels, kernel_size=3, stride=stride, padding=1+i, dilation=1+i, groups=G, bias=False),
nn.BatchNorm2d(in_channels), nn.ReLU(inplace=True)))
self.gap = nn.AdaptiveAvgPool2d((1, 1))
self.fc1 = nn.Sequential(nn.Conv2d(in_channels, d, kernel_size=1, stride=1, padding=0, bias=False),
nn.BatchNorm2d(d), nn.ReLU(inplace=True))
self.fc2_branches = nn.ModuleList([])
for i in range(M):
self.fc2_branches.append(
nn.Sequential(nn.Conv2d(d, in_channels, kernel_size=1, stride=1, padding=0, bias=False),
nn.BatchNorm2d(in_channels), nn.ReLU(inplace=True)))
self.softmax = nn.Softmax(dim=1)
def forward(self, x):
batch_size = x.shape[0]
features = torch.cat([conv(x) for conv in self.conv_branches], dim=1)
features = features.view(batch_size, self.M, self.in_channels, features.shape[2], features.shape[3])
features_U = torch.sum(features, dim=1)
features_S = self.gap(features_U)
features_Z = self.fc1(features_S)
attention_vectors = torch.cat([fc(features_Z) for fc in self.fc2_branches], dim=1)
attention_vectors = attention_vectors.view(batch_size, self.M, self.in_channels, 1, 1)
attention_vectors = self.softmax(attention_vectors)
features_V = torch.sum(features * attention_vectors, dim=1)
return features_V
class SKUnit(nn.Module):
def __init__(self,
in_channels,
mid_channels,
out_channels,
stride=1, M=2, G=32, r=16, L=32):
super(SKUnit, self).__init__()
self.conv1x1_1 = nn.Sequential(nn.Conv2d(in_channels, mid_channels, kernel_size=1, stride=1, padding=0, bias=False),
nn.BatchNorm2d(mid_channels), nn.ReLU(inplace=True))
self.skconv_2 = SKConv(mid_channels, stride, M, G, r, L)
self.conv1x1_3 = nn.Sequential(nn.Conv2d(mid_channels, out_channels, kernel_size=1, stride=1, padding=0, bias=False),
nn.BatchNorm2d(out_channels), nn.ReLU(inplace=True))
# if in_channels == out_channels: # when dim not change, input_features could be added diectly to out
self.shortcut = nn.Sequential()
if stride != 1 or in_channels != out_channels: # when dim not change, input_features should also change dim to be added to out
self.shortcut = nn.Sequential(
nn.Conv2d(in_channels, out_channels, 1, stride=stride, bias=False),
nn.BatchNorm2d(out_channels)
)
self.relu = nn.ReLU(inplace=True)
def forward(self, x):
residual = x
out = self.conv1x1_1(x)
out = self.skconv_2(out)
out = self.conv1x1_3(out)
return self.relu(out + self.shortcut(residual))
class SKNet(nn.Module):
"""
ResNext-based Selective Kernel Network
"""
def __init__(self,
block,
num_blocks,
strides_list=[1, 2, 2, 2],
num_classes=100,
num_channels=3,
M=2, G=32, r=16, L=32):
super(SKNet, self).__init__()
self.conv = nn.Sequential(
nn.Conv2d(num_channels, 64, 7, stride=2, padding=3, bias=False),
nn.BatchNorm2d(64),
nn.ReLU(inplace=True))
self.pool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
self.stage_1 = self._make_layer(block, num_blocks[0], in_channels=64, mid_channels=128, out_channels=256, stride=strides_list[0], M=M, G=G, r=r, L=L)
self.stage_2 = self._make_layer(block, num_blocks[1], in_channels=256, mid_channels=256, out_channels=512, stride=strides_list[1], M=M, G=G, r=r, L=L)
self.stage_3 = self._make_layer(block, num_blocks[2], in_channels=512, mid_channels=512, out_channels=1024, stride=strides_list[2], M=M, G=G, r=r, L=L)
self.stage_4 = self._make_layer(block, num_blocks[3], in_channels=1024, mid_channels=1024, out_channels=2048, stride=strides_list[3], M=M, G=G, r=r, L=L)
self.avg = nn.AdaptiveAvgPool2d((1, 1))
self.fc = nn.Linear(512 * 4, num_classes)
def _make_layer(self, block, num_block, in_channels, mid_channels, out_channels, stride=1, M=2, G=32, r=16, L=32):
layers = [block(in_channels, mid_channels, out_channels, stride=stride, M=M, G=G, r=r, L=L)]
for _ in range(1, num_block):
layers.append(block(out_channels, mid_channels, out_channels))
return nn.Sequential(*layers)
def forward(self, x):
x = self.conv(x)
x = self.pool(x)
x = self.stage_1(x)
x = self.stage_2(x)
x = self.stage_3(x)
x = self.stage_4(x)
x = self.avg(x)
x = x.view(x.size(0), -1)
x = self.fc(x)
return x
def SKNet26(num_classes=1000):
return SKNet(SKUnit, [2, 2, 2, 2], [1, 2, 2, 2], num_classes)
def SKNet50(num_classes=1000):
return SKNet(SKUnit, [2, 2, 2, 2], [1, 2, 2, 2], num_classes)
def SKNet101(num_classes=1000):
return SKNet(SKUnit, [2, 2, 2, 2], [1, 2, 2, 2], num_classes)
if __name__=='__main__':
x = torch.rand(8, 3, 224, 224)
model = SKNet26()
out = model(x)