안녕하세요. 지난 포스팅의 선형대수학 - 그람-슈미트 과정에서는 내적공간의 비직교 기저로부터 정규직교 기저를 만들 수 있는 그람-슈미트 과정 (Gram-Schmitz Process)에 대해서 알아보았습니다. 또한, 실제로 예시를 통해 적용해보았죠. 이를 통해, 0이 아닌 유한차원을 가지는 임의의 내적공간은 항상 정규직교 기저를 가짐을 보였습니다. 뿐만 아니라, 내적공간의 임의의 벡터들은 정규직교 기저를 통해 임의의 벡터와 기저 사이의 선형결합을 통해 표현할 수 있음을 보였습니다. 오늘은 직교집합을 주제로한 새로운 내용을 말씀드리고자 합니다. 바로 직교여공간 (Orthogonal Complement)입니다. 이 역시 앞으로 배울 고급 선형대수 주제에서 빼놓을 수 없는 주제이기 때문에 알아두시면 큰 도움이 될 거 같습니다.
정의1. 직교여공간 (Orthogonal Complement)
$S$를 내적공간 $V$의 공집합이 아닌 부분집합이라고 하자. 우리는 $S^{\perp}$를 부분집합 $S$ 내의 모든 벡터들에 직교하는 내적공간 $V$의 벡터들의 집합으로 정의한다. 즉, $S^{\perp} = \{ x \in V | \langle x, y \rangle = 0 \text{ for all } y \in S \}$으로 정의된다. 이때, $S^{\perp}$는 집합 $S$의 직교여공간 (Orthogonal Complement)로 불린다.
Let $S$ be a nonempty subset of an inner product space $V$. We define $S^{\perp}$ to be the set of all vectors in $V$ that are orthogonal to every vector in $S$, that is, $S^{\perp} = \{ x \in V | \langle x, y \rangle = 0 \text{ for all } y \in S \}$. The set $S^{\perp}$ is called the orthogonal complement of $S$.
설명
가장 간단한 두 가지 경우를 고려해보겠습니다. 바로 $\{ 0 \}^{\perp}$와 $V^{\perp}$이죠. 이 두 집합은 어떤 벡터들을 가지고 있을까요?
1). 직교여공간의 정의에 따르면 $\{ 0 \}^{\perp}$는 다음과 같이 쓸 수 있다.
$$\begin{align*} \{ 0 \}^{\perp} &= \{ x \in V | \langle x, y \rangle = 0 \text{ for all } y \in \{ 0 \} \} \\ &= \{ x \in V | \langle x, 0 \rangle = 0 \} \end{align*}$$
이때, 임의의 벡터 $x \in V$에 대해서 항상 $\langle x, 0 \rangle = 0$이므로 $\{ 0 \}^{\perp} = V$이다.
2). 직교여공간의 정의에 따르면 $V^{\perp}$는 다음과 같이 쓸 수 있다.
$$\begin{align*} V^{\perp} &= \{ x \in V | \langle x, y \rangle = 0 \text{ for all } y \in V \} \end{align*}$$
이때, 임의의 벡터 $x \in V$에 대해 항상 $\langle x, y \rangle = 0$을 만족하는 벡터 $y \in V$는 영벡터밖에 없기 때문에 $V^{\perp} = \{ 0 \}$이다.
아직 감이 안오실 거 같습니다. 그렇다면 이번 예제는 어떨까요? 바로 내적공간 $V = \mathbb{R}^{3}$의 부분집합 $S = \{ e_{3} \}$가 주어졌을 때 $S^{\perp}$를 찾아보도록 하겠습니다.
직교여공간의 정의에 따르면 $S^{\perp}$는 다음과 같이 쓸 수 있다.
$$\begin{align*} S^{\perp} &= \{ x \in V | \langle x, y \rangle = 0 \text{ for all } y \in \{ e_{3} \} \} \\ &= \{ x \in V | \langle x, e_{3} \rangle = 0 \} \end{align*}$$
이때, $V = \mathbb{R}^{3}$이므로 $x = (a, b, c)$라고 두면 다음과 같이 내적을 풀 수 있다.
$$\begin{align*} \langle x, e_{3} \rangle &= \langle (a, b, c), (0, 0, 1) \rangle \\ &= c = 0 \end{align*}$$
즉, $S^{\perp} = \{ a, b \in \mathbb{R} | (a, b, 0) \} = xy\text{-plane}$이다.
위 추가 예시를 통해 굉장히 중요한 직관을 얻을 수 있습니다. 만약, 3차원 공간에서 직선에 대한 직교여공간이라고 한다면 이는 해당 직선이 수직으로 관통하는 평면이 될 것 입니다. 반대로 3차원 공간에서 평면에 대한 직교여공간이라고 한다면 이는 해당 평면을 수직으로 관통하는 직선이 될 것 입니다. 이 정도만 생각하셔도 정리들을 이해하는 데 큰 무리는 없습니다. 이제 이 개념을 활용해서 다음 문제를 풀어보도록 하겠습니다.
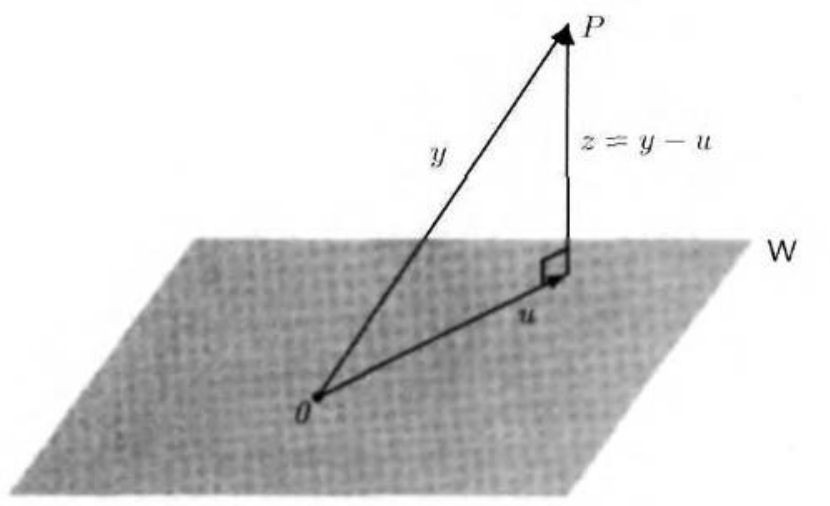
위 그림과 같이 점 $P$와 평면 $W$가 주어졌다고 가정하겠습니다. 이때, 점 $P$에서 평면 $W$까지의 최단거리를 구해보도록 하죠. 아마 이 문제는 고등학교 때 기하와벡터 파트에 나오는 것으로 기억합니다. 저희는 이를 선형대수학을 활용해서 구하도록 하겠습니다.
이 문제를 다시 써보면 원점 $O$에서 점 $P$로 이어지는 벡터를 $y$ 그리고 점 $P$가 평면 $W$에 정사영시켰을 때 점 $P^{'}$와 원점 $O$ 사이의 벡터를 $u$라고 두도록 하겠습니다. 그러면 점 $P$와 점 $P^{'}$ 사이의 벡터는 $z = y - u$라고 쓸 수 있으므로 점과 평면 사이의 최단거리는 $\lVert z \rVert = \lVert y - u \rVert$입니다. 이때, 눈여겨봐야할 것은 $z$는 평면 $W$에 직교하는 직선이라는 점 이죠. 따라서, 직교여공간의 정의에 의해 $z \in W^{\perp}$가 됩니다. 이제 저희가 해야하는 것은 $y = u + z$를 만족하는 2개의 벡터 $u \in W$와 $z \in W^{\perp}$가 유일하게 존재함을 보일 것 입니다.
정리1
$W$를 유한차원의 내적공간 $V$의 부분공간 그리고 $y \in V$라고 하자. 그러면 $y = u + z$를 만족하는 2개의 벡터 $u \in W$와 $z \in W^{\perp}$가 유일하게 존재한다. 뿐만 아니라, $\{ v_{1}, \dots, v_{k} \}$가 부분공간 $W$의 정규직교기저라면 $u = \sum_{i = 1}^{k} \langle y, v_{i} \rangle v_{i}$이다.
설명
증명은 크게 2가지로 진행됩니다. 먼저 $z \in W^{\perp}$를 보이고 $u$와 $z$의 유일성을 증명합니다. 이 과정에서 내적의 성질과 직교기저의 성질을 활용하면 됩니다.
Proof)
$\{ v_{1}, \dots, v_{k} \}$를 부분공간 $W$의 직교기저 그리고 $u$를 이전에 정의한 대로 $z = y - u$를 만족하는 벡터라고 하자. 이는 자명하게 $u \in W$이고 $y = u + z$이다.
1). $z \in W^{\perp}$
벡터 $z$가 부분공간 $W$의 직교여공간 $W^{\perp}$에 속한다는 것을 증명하는 것은 직교여공간의 정의에 따라 벡터 $z$가 임의의 $v_{j} \in W$에 대해 모두 직교한다는 것을 보이는 것과 동치이다. 따라서, 임의의 $j$에 대해서 우리는 $z$와 $v_{j}$ 사이의 내적을 다음과 같이 쓸 수 있다.
$$\begin{align*} \langle z, v_{j} \rangle &= \langle y - u, v_{j} \rangle \\ &= \langle y - \sum_{i = 1}^{k} \langle y, v_{i} \rangle v_{i}, v_{j} \rangle \\ &= \langle y, v_{j} \rangle - \sum_{i = 1}^{k} \langle y, v_{i} \rangle \langle v_{i}, v_{j} \rangle \\ &= \langle y, v_{j} \rangle \langle y, v_{j} \rangle = 0 \end{align*}$$
$\langle z, v_{j} \rangle = 0$이므로 $z \in W^{\perp}$이다.
2). $u$와 $z$는 유일하다.
$y = u + z = u^{'} + z^{'}$를 만족하는 또다른 벡터 $u^{'} \in W$와 $z^{'} \in W^{\perp}$가 존재한다고 가정하자. 그러면 $u - u^{'} = z - z^{'} \in W \cap W^{\perp} = \{ 0 \}$이므로 $u = u^{'}$ 이고 $z = z^{'}$이므로 $u$와 $z$는 유일하다.
따름정리1-1
$W$를 유한차원의 내적공간 $V$의 부분공간 그리고 $y \in V$라고 하자. 벡터 $u \in W$가 벡터 $y$와 가장 가까운 벡터이다. 즉, 임의의 벡터 $x \in W$에 대해서 $\lVert y - x \rVert \ge \lVert y - u \rVert$이고 오직 $x = u$일 때만 등식이 성립한다.
Proof)
정리1에 의해 $y = u + z$이고 $z \in W^{\perp}$임을 알 수 있다. 이때, 임의의 벡터 $x \in W$가 주어졌다고 하면 $u - x$는 $z$에 직교한다. 따라서, 다음과 같이 식을 전개할 수 있다.
$$\begin{align*} \lVert y - x \rVert^{2} &= \lVert (u + z) - x \rVert^{2} \\ &= \lVert (u - x) + z \rVert^{2} \\ &= \lVert u - x \rVert^{2} + \lVert z \rVert^{2} \\ &= \lVert z \rVert^{2} = \lVert y - u \rVert \end{align*}$$
이제 $\lVert y - x \rVert = \lVert y - u \rVert$라고 가정하자. 그러면 $\lVert u - x \rVert^{2} + \lVert z \rVert^{2} = \lVert z \rVert^{2}$이기 때문에 $\lVert u - x \rVert = 0$이므로 $x = u$이다.
정리1과 따름정리1-1을 통해 평면 $W$과 점 $P$ 사이의 최단거리를 구하는 방법은 원점 $O$에서 점 $P$로 이어지는 벡터 $y$ 그리고 점 $P$가 평면 $W$에 정사영시켰을 때 점 $P^{'}$와 원점 $O$ 사이의 벡터 $u$를 각각 정한 뒤 두 벡터의 차의 노름 $\lVert y - u \rVert = \lVert z \rVert$를 구하면 됩니다. 이때, 이 두 벡터 $z$와 $u$는 유일하기 때문에 이 최단거리 역시 유일하게 결정됩니다.
마지막으로 직교여공간의 성질을 확인하고 마무리하도록 하겠습니다.
정리2
$S = \{ v_{1}, \dots, v_{k} \}$를 $n$차원의 내적공간 $V$의 정규직교집합 이라고 하면 다음 명제들이 성립한다.
(a). $S$는 내적공간 $V$의 정규직교 기저 $\{ v_{1}, \dots, v_{k}, v_{k + 1}, \dots, v_{n} \}$로 확장될 수 있다.
(b). $W = \text{span} (S)$이면 $S_{1} = \{ v_{k + 1}, \dots, v_{n} \}$은 $W$의 직교여공간 $W^{\perp}$의 정규직교 기저이다.
(c). $W$를 $V$의 부분공간이라고 하면 $\text{dim} (V) = \text{dim} (W) + \text{dim} (W^{\perp})$이다.
Proof)
(a). 선형대수학 - 기저와 차원의 정리3 (Replacement Theorem)에 의해 집합 $S$는 $W$의 순서 기저 $S^{'} = \{ v_{1}, \dots, v_{k}, w_{k + 1}, \dots, w_{n} \}$으로 확장될 수 있다. 이제, $S^{'}$를 선형대수학 - 그람-슈미트 과정의 정리1 (그람-슈미트 정리)를 적용하면 처음 $k$개의 벡터들 ($v_{1}, \dots, v_{k}$)은 이미 직교하기 때문에 보존되고 남은 $n - k$개의 벡터들 ($w_{k + 1}, \dots, w_{n}$)은 직교기저로 만들어진다. 이때, 정규화를 통해 최종적으로 정규직교 기저 $S^{'}$를 만들어 낼 수 있다.
(b). $S_{1}$의 기저의 부분집합이기 때문에 선형독립이다. 또한, $S_{1}$의 각 벡터들은 $S$와 모두 직교하기 때문에 $W$와도 직교한다. 따라서, $S_{1}$은 $W^{\perp}$의 부분집합이다. 이때, 임의의 벡터 $x \in V$에 대해서 선형대수학 - 그람-슈미트 과정의 정리2에 의해 $x = \sum_{i = 1}^{k} \langle x, v_{i} \rangle v_{i}$이다. 만약, $x \in W^{\perp}$라면 모든 $1 \le i \le k$에 대해서 $\langle x, v_{i} \rangle = 0$이다. 따라서, $x = \sum_{i = k + 1}^{n} \langle x, v_{i} \rangle v_{i} \in \text{span}(S_{1})$이다. 그러므로, $S_{1}$은 $W^{\perp}$의 정규직교 기저이다.
(c). 내적공간 $V$의 부분공간 $W$는 정규직교 기저 $\{ v_{1}, \dots, v_{k} \}$를 가지고 있기 때문에 유한차원을 가지는 내적공간이다. 두 명제 (a)와 (b)에 의해 $\text{dim} (V) = n = k + (n - k) = \text{dim} (W) + \text{dim} (W^{\perp})$를 만족한다.
오늘은 직교여공간의 정의와 이를 활용한 점-평면 간 최단거리 문제 그리고 직교여공간의 성질에 대해서 알아보았습니다. 특히, 정리2에서는 내적공간의 정규직교 기저를 찾으면 이를 서로소인 두 기저로 만들면 각 부분공간은 서로 직교여공간이 되고 각 기저집합은 각 부분공간의 기저가 됨을 보였습니다. 지금까지 저희는 내적공간의 성질을 주로 살펴보았습니다. 하지만, 선형대수학에서 중요한 주제 중 하나는 바로 선형변환입니다. 그렇다면 이 선형변환과 직교성 사이의 관계도 굉장히 궁금해집니다. 다음 포스팅에서는 이를 알아볼 수 있는 수반연산자 (Adjoint operator)와 그 성질에 대해서 알아보도록 하겠습니다.
참고문헌
Linear Algebra (Stephan. H)
'수학 > 선형대수학' 카테고리의 다른 글
| 선형대수학 - 최소제곱법 (0) | 2023.09.01 |
|---|---|
| 선형대수학 - 수반연산자 (0) | 2023.08.15 |
| 선형대수학 - 그람-슈미트 과정 (0) | 2023.08.06 |
| 선형대수학 - 직교 기저 (0) | 2023.08.03 |
| 선형대수학 - 노름과 직교성 (0) | 2023.08.01 |
안녕하세요. 지난 포스팅의 선형대수학 - 그람-슈미트 과정에서는 내적공간의 비직교 기저로부터 정규직교 기저를 만들 수 있는 그람-슈미트 과정 (Gram-Schmitz Process)에 대해서 알아보았습니다. 또한, 실제로 예시를 통해 적용해보았죠. 이를 통해, 0이 아닌 유한차원을 가지는 임의의 내적공간은 항상 정규직교 기저를 가짐을 보였습니다. 뿐만 아니라, 내적공간의 임의의 벡터들은 정규직교 기저를 통해 임의의 벡터와 기저 사이의 선형결합을 통해 표현할 수 있음을 보였습니다. 오늘은 직교집합을 주제로한 새로운 내용을 말씀드리고자 합니다. 바로 직교여공간 (Orthogonal Complement)입니다. 이 역시 앞으로 배울 고급 선형대수 주제에서 빼놓을 수 없는 주제이기 때문에 알아두시면 큰 도움이 될 거 같습니다.
정의1. 직교여공간 (Orthogonal Complement)
$S$를 내적공간 $V$의 공집합이 아닌 부분집합이라고 하자. 우리는 $S^{\perp}$를 부분집합 $S$ 내의 모든 벡터들에 직교하는 내적공간 $V$의 벡터들의 집합으로 정의한다. 즉, $S^{\perp} = \{ x \in V | \langle x, y \rangle = 0 \text{ for all } y \in S \}$으로 정의된다. 이때, $S^{\perp}$는 집합 $S$의 직교여공간 (Orthogonal Complement)로 불린다.
Let $S$ be a nonempty subset of an inner product space $V$. We define $S^{\perp}$ to be the set of all vectors in $V$ that are orthogonal to every vector in $S$, that is, $S^{\perp} = \{ x \in V | \langle x, y \rangle = 0 \text{ for all } y \in S \}$. The set $S^{\perp}$ is called the orthogonal complement of $S$.
설명
가장 간단한 두 가지 경우를 고려해보겠습니다. 바로 $\{ 0 \}^{\perp}$와 $V^{\perp}$이죠. 이 두 집합은 어떤 벡터들을 가지고 있을까요?
1). 직교여공간의 정의에 따르면 $\{ 0 \}^{\perp}$는 다음과 같이 쓸 수 있다.
$$\begin{align*} \{ 0 \}^{\perp} &= \{ x \in V | \langle x, y \rangle = 0 \text{ for all } y \in \{ 0 \} \} \\ &= \{ x \in V | \langle x, 0 \rangle = 0 \} \end{align*}$$
이때, 임의의 벡터 $x \in V$에 대해서 항상 $\langle x, 0 \rangle = 0$이므로 $\{ 0 \}^{\perp} = V$이다.
2). 직교여공간의 정의에 따르면 $V^{\perp}$는 다음과 같이 쓸 수 있다.
$$\begin{align*} V^{\perp} &= \{ x \in V | \langle x, y \rangle = 0 \text{ for all } y \in V \} \end{align*}$$
이때, 임의의 벡터 $x \in V$에 대해 항상 $\langle x, y \rangle = 0$을 만족하는 벡터 $y \in V$는 영벡터밖에 없기 때문에 $V^{\perp} = \{ 0 \}$이다.
아직 감이 안오실 거 같습니다. 그렇다면 이번 예제는 어떨까요? 바로 내적공간 $V = \mathbb{R}^{3}$의 부분집합 $S = \{ e_{3} \}$가 주어졌을 때 $S^{\perp}$를 찾아보도록 하겠습니다.
직교여공간의 정의에 따르면 $S^{\perp}$는 다음과 같이 쓸 수 있다.
$$\begin{align*} S^{\perp} &= \{ x \in V | \langle x, y \rangle = 0 \text{ for all } y \in \{ e_{3} \} \} \\ &= \{ x \in V | \langle x, e_{3} \rangle = 0 \} \end{align*}$$
이때, $V = \mathbb{R}^{3}$이므로 $x = (a, b, c)$라고 두면 다음과 같이 내적을 풀 수 있다.
$$\begin{align*} \langle x, e_{3} \rangle &= \langle (a, b, c), (0, 0, 1) \rangle \\ &= c = 0 \end{align*}$$
즉, $S^{\perp} = \{ a, b \in \mathbb{R} | (a, b, 0) \} = xy\text{-plane}$이다.
위 추가 예시를 통해 굉장히 중요한 직관을 얻을 수 있습니다. 만약, 3차원 공간에서 직선에 대한 직교여공간이라고 한다면 이는 해당 직선이 수직으로 관통하는 평면이 될 것 입니다. 반대로 3차원 공간에서 평면에 대한 직교여공간이라고 한다면 이는 해당 평면을 수직으로 관통하는 직선이 될 것 입니다. 이 정도만 생각하셔도 정리들을 이해하는 데 큰 무리는 없습니다. 이제 이 개념을 활용해서 다음 문제를 풀어보도록 하겠습니다.

위 그림과 같이 점 $P$와 평면 $W$가 주어졌다고 가정하겠습니다. 이때, 점 $P$에서 평면 $W$까지의 최단거리를 구해보도록 하죠. 아마 이 문제는 고등학교 때 기하와벡터 파트에 나오는 것으로 기억합니다. 저희는 이를 선형대수학을 활용해서 구하도록 하겠습니다.
이 문제를 다시 써보면 원점 $O$에서 점 $P$로 이어지는 벡터를 $y$ 그리고 점 $P$가 평면 $W$에 정사영시켰을 때 점 $P^{'}$와 원점 $O$ 사이의 벡터를 $u$라고 두도록 하겠습니다. 그러면 점 $P$와 점 $P^{'}$ 사이의 벡터는 $z = y - u$라고 쓸 수 있으므로 점과 평면 사이의 최단거리는 $\lVert z \rVert = \lVert y - u \rVert$입니다. 이때, 눈여겨봐야할 것은 $z$는 평면 $W$에 직교하는 직선이라는 점 이죠. 따라서, 직교여공간의 정의에 의해 $z \in W^{\perp}$가 됩니다. 이제 저희가 해야하는 것은 $y = u + z$를 만족하는 2개의 벡터 $u \in W$와 $z \in W^{\perp}$가 유일하게 존재함을 보일 것 입니다.
정리1
$W$를 유한차원의 내적공간 $V$의 부분공간 그리고 $y \in V$라고 하자. 그러면 $y = u + z$를 만족하는 2개의 벡터 $u \in W$와 $z \in W^{\perp}$가 유일하게 존재한다. 뿐만 아니라, $\{ v_{1}, \dots, v_{k} \}$가 부분공간 $W$의 정규직교기저라면 $u = \sum_{i = 1}^{k} \langle y, v_{i} \rangle v_{i}$이다.
설명
증명은 크게 2가지로 진행됩니다. 먼저 $z \in W^{\perp}$를 보이고 $u$와 $z$의 유일성을 증명합니다. 이 과정에서 내적의 성질과 직교기저의 성질을 활용하면 됩니다.
Proof)
$\{ v_{1}, \dots, v_{k} \}$를 부분공간 $W$의 직교기저 그리고 $u$를 이전에 정의한 대로 $z = y - u$를 만족하는 벡터라고 하자. 이는 자명하게 $u \in W$이고 $y = u + z$이다.
1). $z \in W^{\perp}$
벡터 $z$가 부분공간 $W$의 직교여공간 $W^{\perp}$에 속한다는 것을 증명하는 것은 직교여공간의 정의에 따라 벡터 $z$가 임의의 $v_{j} \in W$에 대해 모두 직교한다는 것을 보이는 것과 동치이다. 따라서, 임의의 $j$에 대해서 우리는 $z$와 $v_{j}$ 사이의 내적을 다음과 같이 쓸 수 있다.
$$\begin{align*} \langle z, v_{j} \rangle &= \langle y - u, v_{j} \rangle \\ &= \langle y - \sum_{i = 1}^{k} \langle y, v_{i} \rangle v_{i}, v_{j} \rangle \\ &= \langle y, v_{j} \rangle - \sum_{i = 1}^{k} \langle y, v_{i} \rangle \langle v_{i}, v_{j} \rangle \\ &= \langle y, v_{j} \rangle \langle y, v_{j} \rangle = 0 \end{align*}$$
$\langle z, v_{j} \rangle = 0$이므로 $z \in W^{\perp}$이다.
2). $u$와 $z$는 유일하다.
$y = u + z = u^{'} + z^{'}$를 만족하는 또다른 벡터 $u^{'} \in W$와 $z^{'} \in W^{\perp}$가 존재한다고 가정하자. 그러면 $u - u^{'} = z - z^{'} \in W \cap W^{\perp} = \{ 0 \}$이므로 $u = u^{'}$ 이고 $z = z^{'}$이므로 $u$와 $z$는 유일하다.
따름정리1-1
$W$를 유한차원의 내적공간 $V$의 부분공간 그리고 $y \in V$라고 하자. 벡터 $u \in W$가 벡터 $y$와 가장 가까운 벡터이다. 즉, 임의의 벡터 $x \in W$에 대해서 $\lVert y - x \rVert \ge \lVert y - u \rVert$이고 오직 $x = u$일 때만 등식이 성립한다.
Proof)
정리1에 의해 $y = u + z$이고 $z \in W^{\perp}$임을 알 수 있다. 이때, 임의의 벡터 $x \in W$가 주어졌다고 하면 $u - x$는 $z$에 직교한다. 따라서, 다음과 같이 식을 전개할 수 있다.
$$\begin{align*} \lVert y - x \rVert^{2} &= \lVert (u + z) - x \rVert^{2} \\ &= \lVert (u - x) + z \rVert^{2} \\ &= \lVert u - x \rVert^{2} + \lVert z \rVert^{2} \\ &= \lVert z \rVert^{2} = \lVert y - u \rVert \end{align*}$$
이제 $\lVert y - x \rVert = \lVert y - u \rVert$라고 가정하자. 그러면 $\lVert u - x \rVert^{2} + \lVert z \rVert^{2} = \lVert z \rVert^{2}$이기 때문에 $\lVert u - x \rVert = 0$이므로 $x = u$이다.
정리1과 따름정리1-1을 통해 평면 $W$과 점 $P$ 사이의 최단거리를 구하는 방법은 원점 $O$에서 점 $P$로 이어지는 벡터 $y$ 그리고 점 $P$가 평면 $W$에 정사영시켰을 때 점 $P^{'}$와 원점 $O$ 사이의 벡터 $u$를 각각 정한 뒤 두 벡터의 차의 노름 $\lVert y - u \rVert = \lVert z \rVert$를 구하면 됩니다. 이때, 이 두 벡터 $z$와 $u$는 유일하기 때문에 이 최단거리 역시 유일하게 결정됩니다.
마지막으로 직교여공간의 성질을 확인하고 마무리하도록 하겠습니다.
정리2
$S = \{ v_{1}, \dots, v_{k} \}$를 $n$차원의 내적공간 $V$의 정규직교집합 이라고 하면 다음 명제들이 성립한다.
(a). $S$는 내적공간 $V$의 정규직교 기저 $\{ v_{1}, \dots, v_{k}, v_{k + 1}, \dots, v_{n} \}$로 확장될 수 있다.
(b). $W = \text{span} (S)$이면 $S_{1} = \{ v_{k + 1}, \dots, v_{n} \}$은 $W$의 직교여공간 $W^{\perp}$의 정규직교 기저이다.
(c). $W$를 $V$의 부분공간이라고 하면 $\text{dim} (V) = \text{dim} (W) + \text{dim} (W^{\perp})$이다.
Proof)
(a). 선형대수학 - 기저와 차원의 정리3 (Replacement Theorem)에 의해 집합 $S$는 $W$의 순서 기저 $S^{'} = \{ v_{1}, \dots, v_{k}, w_{k + 1}, \dots, w_{n} \}$으로 확장될 수 있다. 이제, $S^{'}$를 선형대수학 - 그람-슈미트 과정의 정리1 (그람-슈미트 정리)를 적용하면 처음 $k$개의 벡터들 ($v_{1}, \dots, v_{k}$)은 이미 직교하기 때문에 보존되고 남은 $n - k$개의 벡터들 ($w_{k + 1}, \dots, w_{n}$)은 직교기저로 만들어진다. 이때, 정규화를 통해 최종적으로 정규직교 기저 $S^{'}$를 만들어 낼 수 있다.
(b). $S_{1}$의 기저의 부분집합이기 때문에 선형독립이다. 또한, $S_{1}$의 각 벡터들은 $S$와 모두 직교하기 때문에 $W$와도 직교한다. 따라서, $S_{1}$은 $W^{\perp}$의 부분집합이다. 이때, 임의의 벡터 $x \in V$에 대해서 선형대수학 - 그람-슈미트 과정의 정리2에 의해 $x = \sum_{i = 1}^{k} \langle x, v_{i} \rangle v_{i}$이다. 만약, $x \in W^{\perp}$라면 모든 $1 \le i \le k$에 대해서 $\langle x, v_{i} \rangle = 0$이다. 따라서, $x = \sum_{i = k + 1}^{n} \langle x, v_{i} \rangle v_{i} \in \text{span}(S_{1})$이다. 그러므로, $S_{1}$은 $W^{\perp}$의 정규직교 기저이다.
(c). 내적공간 $V$의 부분공간 $W$는 정규직교 기저 $\{ v_{1}, \dots, v_{k} \}$를 가지고 있기 때문에 유한차원을 가지는 내적공간이다. 두 명제 (a)와 (b)에 의해 $\text{dim} (V) = n = k + (n - k) = \text{dim} (W) + \text{dim} (W^{\perp})$를 만족한다.
오늘은 직교여공간의 정의와 이를 활용한 점-평면 간 최단거리 문제 그리고 직교여공간의 성질에 대해서 알아보았습니다. 특히, 정리2에서는 내적공간의 정규직교 기저를 찾으면 이를 서로소인 두 기저로 만들면 각 부분공간은 서로 직교여공간이 되고 각 기저집합은 각 부분공간의 기저가 됨을 보였습니다. 지금까지 저희는 내적공간의 성질을 주로 살펴보았습니다. 하지만, 선형대수학에서 중요한 주제 중 하나는 바로 선형변환입니다. 그렇다면 이 선형변환과 직교성 사이의 관계도 굉장히 궁금해집니다. 다음 포스팅에서는 이를 알아볼 수 있는 수반연산자 (Adjoint operator)와 그 성질에 대해서 알아보도록 하겠습니다.
참고문헌
Linear Algebra (Stephan. H)
'수학 > 선형대수학' 카테고리의 다른 글
| 선형대수학 - 최소제곱법 (0) | 2023.09.01 |
|---|---|
| 선형대수학 - 수반연산자 (0) | 2023.08.15 |
| 선형대수학 - 그람-슈미트 과정 (0) | 2023.08.06 |
| 선형대수학 - 직교 기저 (0) | 2023.08.03 |
| 선형대수학 - 노름과 직교성 (0) | 2023.08.01 |
