안녕하세요. 오늘은 2015년에 나온 FCN이라는 약어로 유명한 Fully Convolutional Networks for Semantic Segmentation을 보도록 하겠습니다.
논문 출처 : https://people.eecs.berkeley.edu/~jonlong/long_shelhamer_fcn.pdf
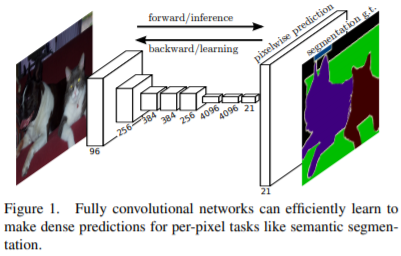
0. Abstract
합성곱 신경망(Convolutional Neural Network; CNN)은 입력 이미지의 특성의 계층을 얻는 강력한 모델입니다. 본 논문에서는 CNN만으로 신경망을 구성하였으며, end-to-end, pixel-to-pixel 방식으로 학습을 하고, semantic segmentation에서 SOTA 성능을 달성하였습니다. 본 논문에서 주의깊게 봐야할 점은 처음부터 끝까지의 모든 layer를 Convolution layer로 구성했다는 점입니다. 본 논문에서는 이를 fully convolutional network(FCN)이라고 표현하였습니다.
이 신경망의 특성은 임의의 사이즈를 갖는 입력 이미지를 사용할 수 있고, 입력 이미지에 대응되는 동일한 크기의 출력 이미지를 효율적인 추론(inference)와 학습(learning)을 할 수 있습니다. 본 논문은 먼저 FCN space에 대한 상세하게 정의, FCN이 spatial dense prediction task로의 응용을 설명, 마지막으로 이전에 나왔던 대표적인 신경망(AlexNet, VGG, GoogleNet)을 FCN으로 바꾸고 segmentation을 위해서 fine-tuned를 통해 이 신경망들이 다른 데이터를 통해 배웠던 데이터 셋의 표현을 transfer하는 방식(transfer learning)으로 진행됩니다. 그리고 deep하고 coarse한 layer의 semantic information과 shallow하고 fine한 layer의 appearance information을 결합하여 더 정확한 segmentation을 결과를 얻게 되었습니다.
본 논문은 PASCAL VOC, NYUDv2, SIFT Flow라는 데이터 셋을 사용하였습니다. 각 데이터 셋에 대한 상세한 설명은 실험부분에서 하도록 하겠습니다.
1. Method
Abstract에서 설명했듯이 본 논문에서는 먼저 FCN에 대해서 설명을 합니다. CNN의 개념을 아시는 분들은 전부 아시겠지만 CNN 내에서 각 layer의 feature map은 3차원 배열($h \times w \times d$)로 구성됩니다. 여기서 $h$와 $w$는 spatial dimension으로 쉽게 말해서 feature map의 세로와 가로를 의미합니다. $d$는 color channel을 의미합니다. $d$ 같은 경우에는 입력 이미지가 color라면 입력 이미지의 shape에서 $d=3$이고 gray scale이면 $d=1$가 됩니다. 또한 여기서 receptive fields라는 용어가 나오는 데 이거는 그림을 통해 설명하면 명확합니다.
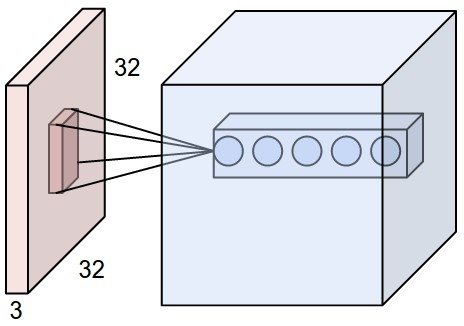
이 그림을 보면 feature map에서 kernel을 통해서 한개의 노드가 생기는 것을 볼 수가 있습니다. 이 한 개의 노드를 만드는데 관여되는 kernel을 receptive fields라고 합니다. 따라서 기본적으로 receptive fields의 크기는 kernel과 동일한 것도 당연히 받아드릴 수 있습니다.
CNN의 중요한 특성 중 하나는 입력 이미지에서 layer(convolution, pooling, activation function)를 통과시키더라도 위치 정보가 불변한다는 점입니다. 이를 translation invariant라고 말합니다. 단지 receptive fields에 해당하는 feature map들의 영역만 영향을 받습니다. 몇 가지 기호에 대해서 언급하면 $\sf x_{i, j}$는 특정 layer의 $(i, j)$ 위치에 해당하는 data vector라고 하겠습니다. 이때 $\sf x_{i, j}$가 vector인 이유는 feature map의 결과가 3차원의 형태로 나올 텐데 특정 위치에 해당하는 data의 이전 layer의 kernel의 개수와 동일하기 때문입니다. 그리고 $\sf y_{i, j}$는 $\sf x_{i, j}$에 의해 계산되는 결과라고 하겠습니다. 이를 수학적으로 표기하면 아래와 같습니다.
$$\sf y_{i, j} = f_{ks}(\{\sf x_{si + \delta i, sj + \delta j}\}_{0 \le \delta i, \delta j \le k})$$
여기서 $k$는 kernel의 크기, $s$는 stride 또는 subsampling factor이라고 합니다. 그리고 $f_{ks}$는 layer의 종류를 의미합니다. 예를들어 convolution layer, average pooling 등이 있습니다.
위 함수식에서 2개의 함수를 합성하면 아래의 transformation rule을 만족한다고 합니다.
(이유는 모르겠네요. 혹시 아시는 분 있으면 댓글로 남겨주시길 바랍니다.)
$$f_{ks} \circ g_{k^{'}s^{'}} = (f \circ g)_{k^{'} + (k - 1)s^{'}, ss^{'}}$$
함수 합성을 적용하는 거는 전체 신경망의 앞에서 뒤로 나아가는 것을 의미합니다. 즉, data가 각종 layer를 통과하는 것을 의미하죠. 그런데 위의 $f$, $g$는 항상 nonlinear layer입니다. 따라서 data는 항상 nonlinear filter를 계산하게 되는 것이죠. 이런 구조를 갖는 신경망을 fully convolutional network라고 정의합니다. 이 FCN은 아무 입력 이미지의 크기에 대해서 연산을 수행할 수 있고 resampling 과정을 통해서 입력 이미지에 대응되는 크기의 출력 이미지를 만들수 있습니다.
1.1. Adapting classifier for dense prediction
그럼 다시 FCN 이전에 유명한 신경망 구조를 다시 생각해보겠습니다. 대표적으로 LeNet, AlexNet, VGG 등등이 있습니다. 이 신경망들은 모두 반드시 고정된 입력 이미지의 크기를 입력받고, nonspatial 출력을 얻습니다. 여기서 nonspatial 출력은 단순한 classification 결과를 의미합니다. 예를 들어 강아지, 고양이 등을 분류하기위해서 출력이 0, 1이 나오는 것입니다. 단순 scalar이기 때문에 nonspatial입니다. 위 예시의 fully connected layer(FCL)는 spatial coordinates를 버리게 됩니다.(Convolution layer으로 진행하다가 Flatten layer로 강제로 dense layer로 만드는 것을 기억해보세요.) 하지만 본 논문에서는 관점을 바꿉니다. FCL의 dense layer 역시 kernel을 통해 얻는 convolution layer로 바라볼 수 있다라는 것입니다. 그래서 아래의 그림과 dense layer였던 마지막 3개의 layer를 convolution layer로 바꿉니다. 이를 convolutionalization이라고 하였습니다.
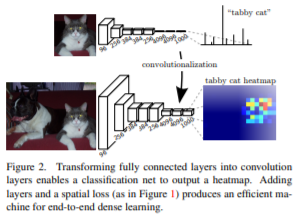
흠 하지만 위의 그림을 봐도 convolutionalization이 어떻게 적용되는 지 모르겠습니다. 제가 그린 그림을 통해서 자세히 알아보도록 하겠습니다.(그림을 잘 못그려서 이해를 부탁드립니다.)
먼저 기존의 convolution layer 이후에 적용되는 fully connected layer를 가지는 신경망부터 보겠습니다.
완벽하게는 아니지만 전형적으로 convolution layer 이후에 적용되는 fully connected layer를 가지고 있습니다. 저희는 이 fully connected layer를 마치 convolution layer처럼 대하고 싶은 것이기 때문에 먼저 이 layer를 90도로 회전시킵니다.
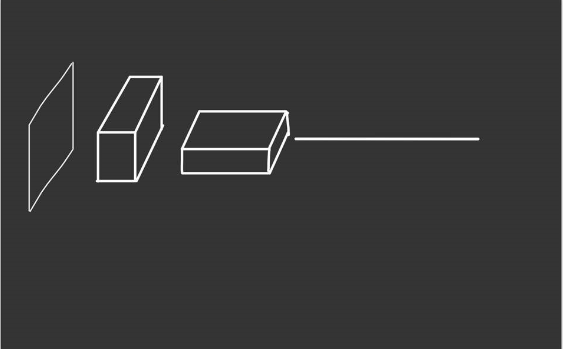
90도로 회전한 결과입니다. 여기에서 fully connected layer의 하나하나의 흔히 노드라고 부르는 요소가 나열되어 있을 것입니다. 그럼 이 노드들을 전부 묶어서 하나의 feature map이라고 보는 것입니다. 아래의 그림을 보시죠.
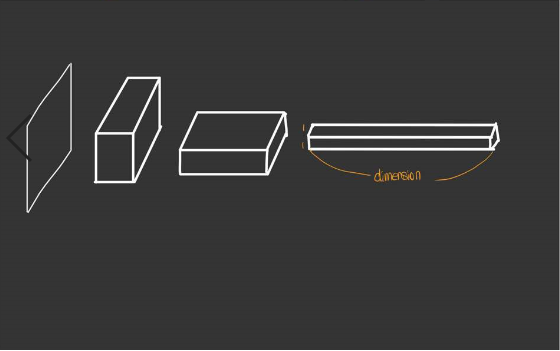
최종적으로 convolutionalization한 결과입니다. 마지막 fully connented layer를 $1 \times 1 \times dimension$의 feature map으로 관점을 바꾸어 생각한 것이 convolutionalization입니다. 만약 fully connected layer가 여러개라면 어떻게 할까요? 동일하게 각각의 dense layer에 대해서 위의 작업을 해주면 됩니다. 본 논문같은 경우에는 convolution layer이후에 3개의 dense layer가 존재하여 각각을 90도로 회전시킨 뒤 다시 한번 각각을 convolution layer로 다루는 것을 볼 수 있습니다.
1.2. shift-and-stitch is filter rarefaction
저는 shift-and-stitch 라는 개념을 처음 들어서 이 부분은 정확하게 이해는 하지 못했습니다. 지금까지 이해한 것을 바탕으로 설명하면 입력 이미지를 조금씩 이동시켜서(shifting) 얻은 출력 영상들을 겹치는(stitch) 것으로 이해하였습니다.(혹시 자세한 관련 논문을 아시는 분들은 댓글로 남겨주시길 바랍니다.)
https://stackoverflow.com/questions/40690951/shift-and-stitch-in-fcn를 참고하여 더 자세히 설명하면 위의 네트워크 구조에서도 보이듯이 Upsampling을 사용하지 않은 경우 입력 이미지에 비해서 최종 출력 이미지의 해상도는 현저하게 낮습니다. 예를 들어 $100 \times 100$의 입력 이미지를 넣으면 $10 \times 10$ 크기의 최종 출력 이미지를 얻게 되겠지요.(출력 이미지의 크기는 변할 수도 있습니다. 예를 들어 설명한 것입니다.) 하지만 저희는 이를 semantic segmentation을 위해서 입력 이미지와 출력 이미지와의 크기를 동일하게 맞춰주어야합니다. 그런데 만약 출력 이미지를 그대로 upsampling하게 되면 당연히 정확하게 되지 않겠죠. 하지만 이러한 과정을 동일한 최종 출력 이미지를 가지고 약간 이동하고 다시 출력을 얻고 그 다음에 다시 조금 이동하고 출력을 얻고 반복합니다. 그러면 출력 이미지가 1개가 아니라 여러 개의 출력 이미지를 얻게 되겠지요. 이렇게 얻은 출력 이미지의 집합을 더 고해상도의 이미지를 얻기 위해서 서로 결합하여 사용하게 됩니다.
아래 그림의 예시를 통해 확인해보겠습니다.
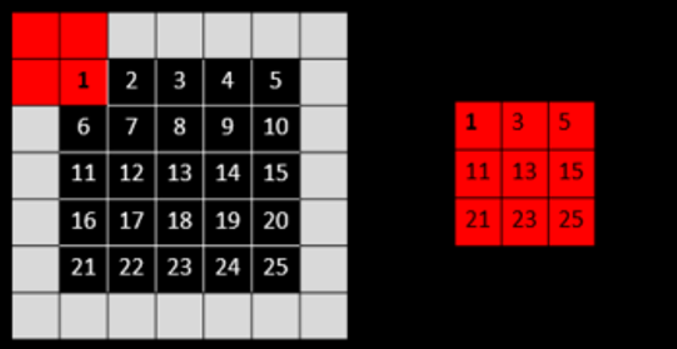
먼저, 빨간색 박스는 $2 \times 2$ 크기의 max pooling filter로 stride는 2로 2칸씩 이동하며 filtering을 하게 됩니다. 오른쪽 $3 \times 3$ 크기의 행렬은 연산 결과를 보여주고 있습니다.
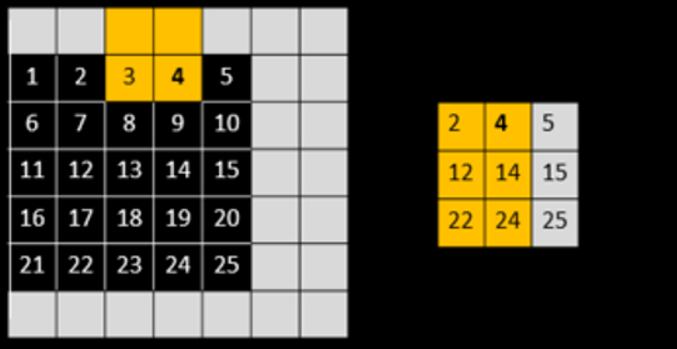
위의 빨간색 박스와 동일한 연산을 하지만 다른 점은 입력 행렬입니다. 비교해보면 왼쪽으로 1 픽셀만큼 이동한 것을 볼 수 있습니다. 따라서 결과도 조금 달라진 것을 볼 수 있습니다. 특히 결과 행렬의 가장 오른쪽이 회색으로 표시되어있는데 이는 입력 이미지를 왼쪽으로 1 픽셀만큼 이동했기 때문에 가장 오른쪽 픽셀 영역은 필요없는 정보가 되기 때문입니다.
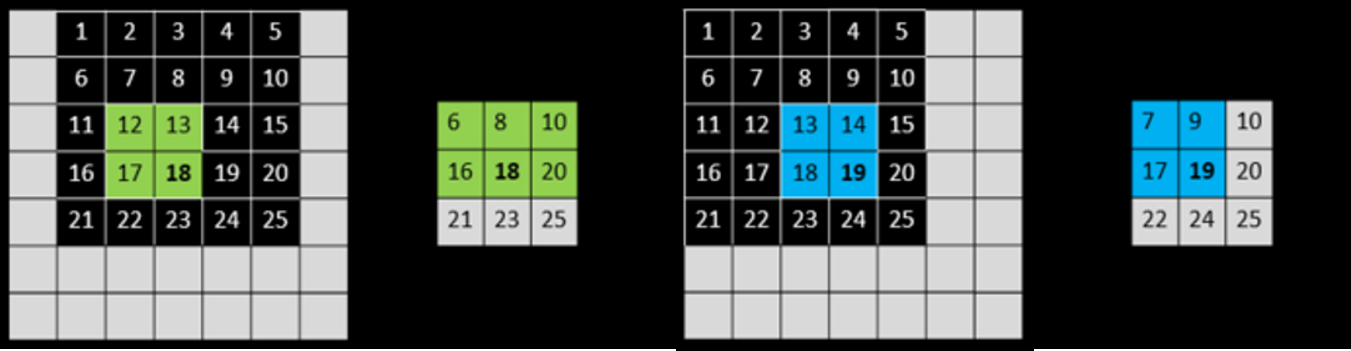
위와 같은 과정을 입력 이미지에서 픽셀 이동 방향을 다르게 잡아 2번 더 반복해주게 됩니다. 물론 더 적용할 수도 있습니다만 총 4번만 적용하였습니다. 이제 이 결과들을 하나로 합칩니다.
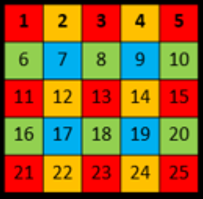
어디서 max pooling 연산이 적용되었는 지에 대한 위치 정보만 저장한다면 위와 같이 다시 입력 이미지와 같은 크기로 채울 수 있을 것입니다.
하지만 이 알고리즘의 치명적은 단점은 계산 비용이 크다는 점입니다. 따라서 계산비용을 낮추기 위해서 본 논문에서는 위와 같은 upsampling을 위해서 트릭을 사용하였습니다. $s$를 stride, $f_{ij}$를 convolution layer의 필터 가중치라고 하겠습니다. 다음 layer의 필터의 가중치를 만약 $s$가 $i$, $j$를 나눌 수 있다면 $f^{'}_{ij} = f_{i/s, j/s}$로 채우고 나누지 못한다면 0으로 채웁니다. 그러나 위의 shift-and-stitch와 완전히 동일한 결과는 얻을 수는 없을 것입니다. 왜냐하면 오직 $s$에 따라서 채워지는 위치가 달라지기 때문이지요. 또한 shift-and-stitch와 다른 점은 max pooling을 사용하지 않고 학습가능한 가중치로 필터를 채운다는 점입니다. 따라서 이 upsampling하는 필터는 적절하게 학습까지 진행할 수 있다는 점이 차이점입니다. 하지만 본 논문에서는 이렇게 길게 설명하고 이 트릭을 사용하지 않았습니다. 왜냐하면 나중에 설명할 skip connection을 통해 구현한 것이 더 효과적이기 때문이죠. 이 절은 가볍게 읽어도 될 것 같습니다.
1.3. Upsampling is backward strided convolution
1.2절의 최종적인 목표는 낮은 해상도의 이미지를 높은 해상도의 이미지로의 upsampling이 목표였습니다. 이를 layer를 중심으로 다시 설명하면 coarse한 결과 이미지를 dense하게 픽셀을 채우는 것입니다. 이를 위한 대표적인 방법으로는 보간법(interpolation)입니다. 예를 들어 bilinear interpolation 같은 경우에는 $y_{ij}$에서 4개의 맞닿는 픽셀을 사용해서 보간을 할 수 있습니다.
본 논문에서는 backward convolution(deconvolution, transposed convolution)이라고 불리는 학습 기반 upsampling을 적용하였습니다. 이렇게 backward convolution과 activation function을 연결하여 nonlinear upsampling을 학습하게 됩니다.
1.4. Patchwise training is loss sampling
그 다음으로 본 논문에서는 patchwise training이라는 개념을 언급합니다. patchwise training이란 모델을 training 할 때 전체 이미지를 넣는 것이 아니라 객체의 주변을 분리한 서브 이미지 즉 patch image를 사용하는 방법을 의미합니다. 여기서 이미지의 부분을 학습하는 patch training과 전체 이미지를 학습하는 fully convolution training은 서로 동일하다고 설명하고 있습니다. 또한 본 논문에서는 fully convolution training이 더 계산적으로 유리하다고 언급하였습니다.
2. Segmentation
본 논문에서는 ILSVRC의 classifier를 FCN으로 변경시키고, pixel 별 loss 계산을 위해서 upsampling을 수행하였습니다. fine-tuning을 통해서 segmentation을 위한 학습을 진행하고, skip connection을 coarse하고 semantic한 layer와 local하고 appearance한 layer 사이에 추가하였습니다. skip connection 추가한 네트워크 구조를 skip architecture라고 하는데 이 skip architecture는 end-to-end로 학습하게 됩니다.
그리고 본 논문에서 사용한 데이터 셋은 PASCAL VOC 2011 segmentation challenge에서 사용된 데이터입니다. 학습을 할 때는 pixel 별 multinomial logistic loss를 사용했습니다. multinomial logistic loss은 아래와 같습니다.
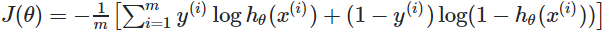
$y$는 true label이고 $h_{\theta}$는 모델입니다. 그리고 $x$는 입력 데이터입니다. 식을 보면 사실장 binary cross-entropy랑 동일한 것을 볼 수 있습니다. 마지막 성능 평가를 위해서 segmentation에서 대표적으로 사용되는 mean pixel intersection over union을 사용했는데 줄여서 IoU라고 하기도 합니다.
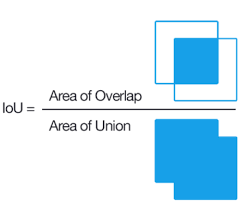
이 그림은 IoU를 간단하게 표현한 것입니다. 실제 mask이미지와 예측된 mask 이미지 사이에 픽셀 단위로 얼마나 겹치는 지를 비율로 표현해주는 metric으로 쓰입니다. 1에 가까울 수록 좋은 성능을 지녔음을 의미합니다.
이제 본 논문에서 말하는 FCN을 만들기 위해서 사용한 네트워크는 AlexNet(ILSVRC2012), VGG(ILSVRC2014), GoogLeNet(ILSVRC2014)를 사용하였습니다. 특히 VGG같은 경우에는 VGG16이 있고 VGG19가 있는데 본 논문에서는 VGG16을 사용하였습니다. 이 네트워크들을 1절에서 언급한 convolutionalozation 과정을 통해서 전부 FCN으로 만들게 됩니다. 이 과정에서 이전에 언급했다 싶이 $1 \times 1$ 합성곱 layer를 사용하였습니다. 그리고 PASCAL 데이터셋의 클래스가 21개(배경을 포함)이기 때문에 원래 Fully connected layer였던 부분은 21개의 채널을 가지는 layer로 바뀌게 됩니다.
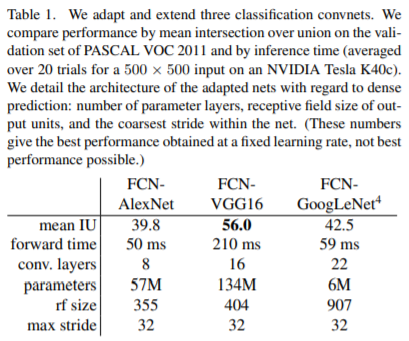
왼쪽의 표는 방금 언급했던 네트워크들을 FCN으로 바꾸고 성능을 측정한 결과입니다. mean IU는 IoU와 동일한 metric인데 VGG16일 때 가장 성능이 좋은 것을 볼 수 있습니다. 하지만 VGG16의 forward time, parameter가 많아서 네트워크 자체가 무거울 것 같습니다. 그래도 전체적으로 봤을 때 성능이 엄청 좋은 것 같지는 않은 것같습니다. 그래서 본 논문에서 skip architecture를 제시하였습니다.
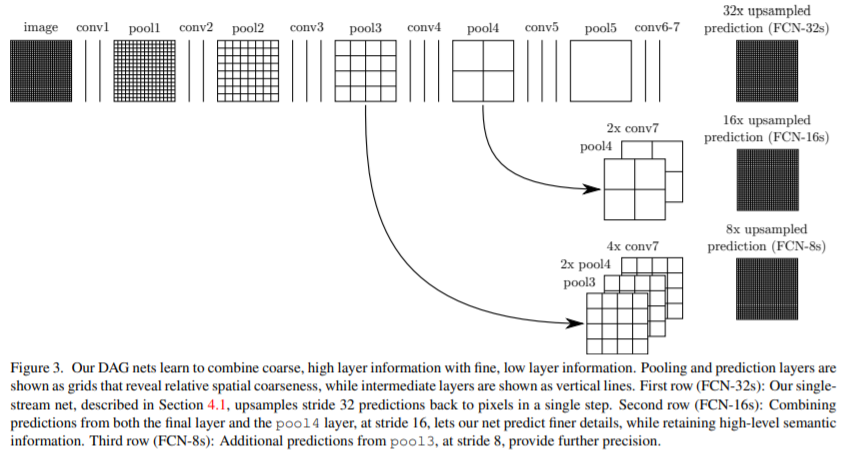
먼저, FCN-16은 pool4 layer에서 $1 \times 1$ 합성곱 layer를 적용하고, 마지막 layer에서 x2 upsampling을 한 뒤에 합칩니다. 마지막 layer에서 x32배 upsampling을 하지 않고 x16배 upsampling하면 입력 이미지의 크기와 동일한 출력 이미지를 얻을 수 있습니다. 그리고 FCN-8은 FCN-16에서 x16배 upsampling하기 전 결과에서 x2 upsampling을 한 뒤에 pool3 layer에 $1 \times 1$ 합성곱 layer를 적용하여 하나로 합칩니다. 그리고 x8배 upsampling을 하게 되는 것입니다. 위의 과정에서 단순히 마지막 layer에서 x32배 upsampling을 한 것은 FCN-32라고 하겠습니다. 각각의 skip architecture의 결과를 시각화하여 확인해보겠습니다.

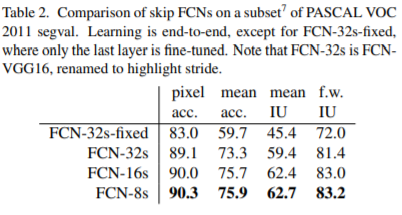
왼쪽 그림을 보면 상위 layer에서 skip connection을 할 수록 결과 mask의 detail이 점점 좋아지는 것을 볼 수 있습니다. 그런데 이는 어떻게 보면 당연한 결과인데 FCN-32의 경우를 생각해보면 한번에 x32배의 upsampling을 하게 되면 엄청나게 많은 정보량이 손실될 것입니다. 따라서 이 정보량 손실을 막기 위해서 fine layer에서 coarse layer로의 skip connection을 적용하게 되면 더 좋은 성능을 얻을 수 있는 것입니다.
왼쪽의 표는 skip connection을 어디에서 했는 지에 따라서 성능이 어떻게 차이가 나는 지 보여주고 있습니다. 실제로 위에서 언급했듯이 fine layer에는 입력 이미지의 세세한 정보가 많이 담겨있을 것입니다. 그래서 convolution layer를 진행하면서 조금씩 손실되는 이미지의 정보를 skip connection을 통해서 손실을 막아주는 역할을 하는 것이죠. 따라서 FCN-16보다 FCN-8이 더 좋은 성능을 보이는 이유는 더 얕은 layer에서 skip connection을 주었기 때문에 더 디테일한 이미지의 정보를 얻을 수 있었기 때문이라고 해석할 수 있을 것 같습니다.
3. 정리
본 논문은 기존에 ILSVRC의 유명한 딥러닝 기반 분류 모델을 sematic segmentation에 맞춰서 수정하여 transfer learning을 수행하고 각 네트워크에 따른 성능을 비교하였다.
segmentation의 per pixel loss를 얻으려면 입력 이미지와 출력 이미지의 shape이 동일해야 하기 때문에 upsampling을 수행하였지만 이 과정에서 많은 정보를 손실하여 성능이 좋지 않았다. 따라서 fine layer에서 coarse layer로의 skip connection을 통해서 정보의 손실을 방지하고 이를 통해 더 좋은 성능을 내는 것을 보여주었다.
