안녕하세요. 지난 포스팅의 선형대수학 - 기저와 차원에서는 어떤 체 $\mathbf{F}$에 대한 벡터공간 $V$가 주어졌을 때 기저(basis) $\beta$와 차원 $\text{dim}(V)$의 정의에 대해서 알아보았습니다. 오늘은 두 개의 벡터공간 $V, W$ 사이의 관계성을 정의하는 선형변환(Linear Transformation)과 선형변환의 영 공간(Null Space)와 치역(Range)까지 알아보도록 하겠습니다.
정의 1. 선형변환(Linear Transformation)
어떤 체 $\mathbf{F}$에 대한 벡터공간 $V$와 $W$가 주어졌을 때, 선형변환(Linear Transformation) $T : V \rightarrow W$는 모든 $\mathbf{u}_{1}, \mathbf{u}_{2} \in V, \alpha \in \mathbf{F}$에 대해서 $T(\mathbf{u}_{1} + \mathbf{u}_{2}) = T(\mathbf{u}_{1}) + T(\mathbf{u}_{2})$이고 $T(\alpha \mathbf{u}_{1}) = \alpha T(\mathbf{u}_{1})$을 만족한다.
Let $V$, and $W$ be vector spaces over a field $\mathbf{F}$. We call a function $T : V \rightarrow W$ a linear transformation from $V$ to $W$ if for all $x, y \in V$ and $c \in \mathbf{F}$, we have
1). $T(\mathbf{x} + \mathbf{y}) = T(\mathbf{x}) + \mathbf{y}$
2). $T(c\mathbf{x}) = cT(\mathbf{x})$
설명
지금까지 저희는 벡터공간 하나가 가지는 다양한 개념 (부분공간, 선형결합, 선형독립, 선형종속, 기저, 차원)에 대한 지식을 쌓았습니다. 그렇다면 자연스럽게 궁금한 것은 벡터공간 두 개가 서로 관계성을 가지는 경우를 생각해볼 수 있겠죠. 마치 함수처럼요! 함수는 두 집합 간의 관계를 어떤 규칙성을 가지고 표현한 것입니다. 선형대수학에서 말하는 선형변환도 마찬가지입니다. 두 벡터공간 간의 관계를 어떤 규칙성을 가지고 표현하지만 정의1과 같이 두 가지 조건을 만족하는 변환을 의미하죠.
Remark1
1). $T$가 선형변환이면 $T(\mathbf{0}) = \mathbf{0}$이다.
2). $T$가 선형변환인 것과 임의의 $\mathbf{x}, \mathbf{y} \in V$와 $c \in \mathbf{F}$에 대해서 $T(c\mathbf{x} + \mathbf{y}) = cT(\mathbf{x}) + T(\mathbf{y})$을 만족하는 것은 동치이다.
3). $T$가 선형변환이면 임의의 $\mathbf{x}, \mathbf{y} \in V$에 대해서 $T(\mathbf{x} - \mathbf{y}) = T(\mathbf{x}) - T(\mathbf{y})$이다.
4). $T$가 선형변환인 것과 임의의 $\mathbf{x}_{1}, \dots, \mathbf{x}_{n} \in V$와 $a_{1}, \dots, a_{n} \in \mathbf{F}$에 대해서 $T(\sum_{i = 1}^{n} a_{i}x_{i}) = \sum_{i = 1}^{n} a_{i} T(x_{i})$를 만족하는 것은 동치이다.
Remark1에서 2)가 가장 중요합니다. 앞으로 어떤 변환이 선형임을 증명할 때는 2)를 사용해서 증명하기 때문이죠. 간단한 선형변환의 예시를 들어보도록 하겠습니다. $T : \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}$인 변환 $T$가 $T(a_{1}, a_{2}) = (2a_{1} + a_{2}, a_{1})$으로 정의되었다고 가정하겠습니다. 그렇다면 $T$가 선형변환임을 증명하기 위해 임의의 $\mathbf{x}, \mathbf{y} \in V = \mathbb{R}^{2}$와 $c \in \mathbb{R}$를 선택하도록 하죠. 그러면 $\mathbf{x} = (b_{1}, b_{2})$ 그리고 $\mathbf{y} = (d_{1}, d_{2})$와 같이 쓸 수 있습니다. 저희는 Remark1의 2)를 사용해서 증명할 예정이기 때문에 $c\mathbf{x} + \mathbf{y} = c(b_{1}, b_{2}) + (d_{1}, d_{2}) = (cb_{1} + d_{1}, cb_{2} + d_{2})$를 변환 $T$에 넣어보겠습니다.
$$\begin{align*} T(c\mathbf{x} + \mathbf{y}) &= T(cb_{1} + d_{1}, cb_{2} + d_{2}) \\ &= (2(cb_{1} + d_{1}) + (cb_{2} + d_{2}), cb_{1} + d_{1}) \\ &= (2c(b_{1} + b_{2}) + 2(d_{1} + d_{2}), cb_{1} + d_{1}) \\ &= c(2(b_{1} + b_{2}), b_{1}) + (2(d_{1} + d_{2}), d_{1}) \\ &= cT(\mathbf{x}) + T(\mathbf{y}) \end{align*}$$
따라서, $T(c\mathbf{x} + \mathbf{y}) = cT(\mathbf{x}) + T(\mathbf{y})$를 만족하기 때문에 $T$는 선형변환입니다. 몇 가지 예시를 통해서 선형변환의 다양한 증명을 보도록 하겠습니다.
예제1. $T_{\theta} : \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}$인 변환 $T_{\theta}(a_{1}, a_{2})$는 벡터 $(a_{1}, a_{2})$를 $\theta$ 만큼 반시계방향으로 회전한다고 하자. 만약 $(a_{1}, a_{2}) = (0, 0)$이라면 $T_{\theta}(0, 0) = (0, 0)$이다. 이때, $T$가 선형변환임을 증명하라.
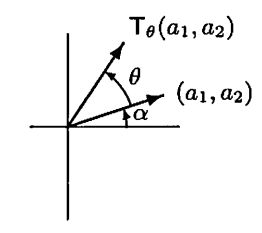
영벡터가 아닌 벡터 $(a_{1}, a_{2}) \in \mathbb{R}^{2}$가 주어졌다고 하자. 여기서 $\alpha$를 위 그림과 같이 벡터 $(a_{1}, a_{2})$와 $x$-축 사이의 각이라고 하자. 또한, $r = \sqrt{a_{1}^{2} + a_{2}^{2}}$이라고 하면 극좌표변환에 의해 $a_{1} = r\cos(\alpha)$ 그리고 $a_{2} = r\sin(\alpha)$라고 둘 수 있다.
여기서 선형변환 $T_{\theta}$는 $x$-축과의 각도가 $\alpha$인 벡터 $(a_{1}, a_{2})$의 각도를 $\theta$만큼 더 회전하기 때문에 변환된 벡터와 $x$-축 사이의 각도는 $\alpha + \theta$이다. 따라서, 선형변환 $T_{\theta}$는 다음과 같이 정리할 수 있다.
$$\begin{align*} T_{\theta}(a_{1}, a_{2}) &= (r\cos(\alpha + \theta), r\sin(\alpha + \theta)) \\ &= (r\cos(\alpha)\cos(\theta) - r\sin(\alpha)\sin(\theta), r\cos(\alpha)\sin(\theta) + r\sin(\alpha)\cos(\theta)) \\ &= (a_{1}\cos(\theta) - a_{2}\sin(\theta), a_{1}\sin(\theta) + a_{2}\cos(\theta)) \end{align*}$$
실제로 $T_{\theta}(0, 0) = (0, 0)$임을 알 수 있다. 이제 $T_{\theta}$가 선형변환임을 증명하기 위해 임의의 $\mathbf{x}, \mathbf{y} \in V = \mathbb{R}^{2}$와 $c \in \mathbb{R}$를 선택한다. 이때, $\mathbf{x} = (b_{1}, b_{2})$ 그리고 $\mathbf{y} = (d_{1}, d_{2})$와 같이 쓸 수 있으며 $c\mathbf{x} + \mathbf{y} = c(b_{1}, b_{2}) + (d_{1}, d_{2}) = (cb_{1} + d_{1}, cb_{2} + d_{2})$를 변환 $T_{\theta}$에 대입한다.
$$\begin{align*} T_{\theta}(c\mathbf{x} + \mathbf{y}) &= T_{\theta}(cb_{1} + d_{1}, cb_{2} + d_{2}) \\ &= ((cb_{1} + d_{1})\cos(\theta) - (cb_{2} + d_{2})\sin(\theta), (cb_{1} + d_{1})\sin(\theta) + (cb_{2} + d_{2})\cos(\theta)) \\ &= c(b_{1}\cos(\theta) - b_{2}\sin(\theta), b_{1}\sin(\theta) + b_{2}\cos(\theta)) + (d_{1}\cos(\theta) - d_{2}\sin(\theta), d_{1}\sin(\theta) + d_{2}\cos(\theta)) \\ &= cT(\mathbf{x}) + T(\mathbf{y})\end{align*}$$
따라서, $T_{\theta}(c\mathbf{x} + \mathbf{y}) = cT_{\theta}(\mathbf{x}) + T_{\theta}(\mathbf{y})$를 만족하기 때문에 $T_{\theta}$는 선형변환이다.
예제2. $T : M_{m \times n}(\mathbf{F}) \rightarrow M_{n \times m}(\mathbf{F})$인 변환 $T$가 $T(A) = A^{t}$로 정의된다고 하자. 이때, $T$가 선형변환임을 증명하라.
$T$가 선형변환임을 증명하기 위해 임의의 $A, B \in V = M_{m \times n}(\mathbf{F})$와 $c \in \mathbf{F}$를 선택한다.
$$\begin{align*} T(cA + B) &= (cA + B)^{t} \\ &= cA^{t} + B^{t} \\ &= cT(A) + T(B) \end{align*}$$
따라서, $T(cA + B) = cT(A) + T(B)$를 만족하기 때문에 $T$는 선형변환이다.
예제3. $T : P_{n}(\mathbb{R}) \rightarrow P_{n - 1}(\mathbb{R})$인 변환 $T(f(x)) = f^{'}(x)$로 정의된다고 하자. 이때, $T$가 선형변환임을 증명하라.
$T$가 선형변환임을 증명하기 위해 임의의 $f, g \in V = P_{n}(\mathbb{R})$와 $c \in \mathbb{R}$를 선택한다.
$$\begin{align*} T((cf + g)(x)) &= (cf + g)^{'}(x) \\ &= cf^{'}(x) + g^{'}(x) \\ &= cT(f(x)) + T(g(x)) \end{align*}$$
따라서, $T((cf + g)(x)) = cT(f(x)) + T(g(x))$를 만족하기 때문에 $T$는 선형변환이다.
예제4. $V = \mathcal{C}(\mathbb{R})$을 실수에서 연속인 실함수들의 집합이라고 하자. $T : V \rightarrow \mathbb{R}$인 변환 $T$가 임의의 실수 $a, b \in \mathbb{R}$에 대해서 $T(f(x)) = \int_{a}^{b} f(t) \; dt$로 정의된다고 하자. 이때, $T$가 선형변환임을 증명하라.
$T$가 선형변환임을 증명하기 위해 임의의 $f, g \in V = \mathcal{C}(\mathbb{R})$와 $c \in \mathbb{R}$를 선택한다.
$$\begin{align*} T((cf + g)(x)) &= \int_{a}^{b} (cf + g)(t) \; dt \\ &= \int_{a}^{b} (cf(t) + g(t)) \; dt \\ &= \int_{a}^{b} cf(t) \; dt + \int_{a}^{b} g(t) \; dt \\ &= c\int_{a}^{b} f(t) \; dt + \int_{a}^{b} g(t) \; dt \\ &= cT(f(x)) + T(g(x)) \end{align*}$$
따라서, $T((cf + g)(x)) = cT(f(x)) + T(g(x))$를 만족하기 때문에 $T$는 선형변환이다.
이를 통해서 저희는 영상 처리에서 나오는 개념인 회전이 왜 선형변환인지 알게 되었습니다. 뿐만 아니라, 전치행렬 역시 선형변환이죠. 다항식 연산인 미분과 적분 역시 선형변환임을 알게 되었습니다. 이 개념들은 앞으로 선형대수학 전반에서 아주 중요하게 사용되니 꼭 기억해주시길 바랍니다.
정의2. 항등변환 (identity transformation)과 영변환 (zero transformation)
어떤 체 $\mathbf{F}$에 대한 벡터공간 $V$와 $W$가 주어졌을 때, $I_{V} : V \rightarrow V$인 변환 $I_{V}$가 임의의 $\mathbf{x} \in V$에 대해서 $I_{V}(\mathbf{x}) = \mathbf{x}$를 만족하면 $I_{V}$를 항등변환 (identity transformation)이라고 한다. 그리고 $T_{\mathbf{0}} : V \rightarrow W$인 변환 $T_{\mathbf{0}}$가 임의의 $\mathbf{x} \in V$에 대해서 $T_{\mathbf{0}}(\mathbf{x}) = \mathbf{0}$를 만족하면 $T_{\mathbf{0}}$을 영변환 (zero transformation)이라고 한다. 이때, 항등변환 $I_{V}$와 영변환 $T_{\mathbf{0}}$ 모두 선형변환이다.
Let $V$, and $W$ be vector spaces over a field $\mathbf{F}$. We define a identity transformation $I_{V} : V \rightarrow V$ by $I_{V}(\mathbf{x}) = \mathbf{x}$ for all $\mathbf{x} \in V$, and a zero transformation $T_{\mathbf{0}} : V \rightarrow W$ by $T_{\mathbf{0}}(\mathbf{x}) = \mathbf{0}$ for all $\mathbf{x} \in V$. These two transformations are linear.
정의3. 영공간 (Null Space)와 치역공간 (Range)
어떤 체 $\mathbf{F}$에 대한 벡터공간 $V$와 $W$가 주어졌을 때, 선형변환 $T : V \rightarrow W$의 영 공간(Null Space)과 치역(Range)는 아래와 같이 정의된다.
1). 영 공간 : $N(T) = \{\mathbf{u} \in V | T(\mathbf{u}) = \mathbf{0}\}$
2). 치역 : $R(T) = \{T(\mathbf{u}) | \mathbf{u} \in V\}$
Let $V$, and $W$ be vector spaces over a field $\mathbf{F}$, and let $T : V \rightarrow W$ be linear.
1). We define the null space $N(T)$ of $T$ to be the set of all vectors $\mathbf{x} \in V$ such that $T(\mathbf{x}) = \mathbf{0}$ :
$$N(T) = \{\mathbf{x} \in V | T(\mathbf{x}) = \mathbf{0}\}$$
2). We define the range $R(T)$ of $T$ to be the subset of $W$ consisting of all vectors in $V$ :
$$R(T) = \{T(\mathbf{x}) \in W | \mathbf{x} \in V\}$$
설명
간단한 예시와 함께 설명해보도록 하겠습니다. 정의2에서의 항등변환과 영변환을 이용해보도록 하죠. 항등변환은 $I_{V} : V \rightarrow V$인 변환 $I_{V}(\mathbf{x}) = \mathbf{x}$를 의미합니다. 이때, 영공간을 구하기 위해서는 $I_{V}(\mathbf{x}) = 0$이 되는 모든 벡터들을 구해야하죠. 하지만, 항등변환의 정의에 의해 $I_{V}(\mathbf{x}) = 0$를 만족하는 벡터는 영벡터가 유일합니다. 따라서, $N(I_{V}) = \{\mathbf{0}\}$이죠. 또한, 항등변환에 의해 $V$의 모든 벡터들이 $V$로 매핑되기 때문에 $R(I_{V}) = V$입니다.
이번에는 영변환을 보도록 하죠. 영변환은 모든 $\mathbf{x} \in V$에 대해서 $T_{\mathbf{0}}(\mathbf{x}) = \mathbf{0}$을 만족하는 선형변환입니다. $T_{\mathbf{x}} = \mathbf{0}$은 그 자체로 영공간의 정의를 따르는 것을 볼 수 있습니다. 즉, $V$의 모든 벡터들이 $\mathbf{0}$으로 매핑되기 때문에 $N(T_{\mathbf{0}}) = V$가 됩니다. 또한, 영변환에 의해 $V$의 모든 벡터들이 $\mathbf{0}$으로 매핑되기 때문에 $R(T_{\mathbf{0}}) = \{\mathbf{0}\}$입니다.
예제5. $T : \mathbb{R}^{3} \rightarrow \mathbb{R}^{2}$에서 $T(a_{1}, a_{2}, a_{3}) = (a_{1} - a_{2}, a_{3})$로 정의된 선형변환이라고 할 때, 영공간과 치역공간을 찾아라.
영공간을 찾기 위해 $T(a_{1}, a_{2}, a_{3}) = (a_{1} - a_{2}, a_{3}) = \mathbf{0}$이라고 두면 $a_{1} = a_{2}$ 그리고 $a_{3} = 0$을 만족하는 모든 3차원 벡터이므로 영공간은 아래와 같다.
$$N(T) = \{(a, a, 0) \in \mathbb{R}^{3} | a \in \mathbf{F}\}$$
치역공간은 매핑되는 공간이 2차원 실수공간과 동일하므로 $R(T) = \mathbb{R}^{2}$이다.
정리 1.
어떤 체 $\mathbf{F}$에 대한 벡터공간 $V$와 $W$가 주어졌을 때, 선형변환 $T : V \rightarrow W$의 영 공간은 $V$의 부분공간이고 치역공간은 $W$의 부분공간이다.
$$N(T) < V$$
$$R(T) < W$$
증명
오랜만에 부분공간을 증명해야하는 정리가 등장하였습니다. 이를 위해서는 부분공간의 정의와 부분공간을 증명하기 위해 몇 가지 기술을 아래의 링크에서 참조해주시길 바랍니다.
선형대수학 - 부분공간
안녕하세요. 지난 포스팅의 선형대수학 - 벡터 공간에서 이어서 오늘은 부분 공간(Subspaces)에 대해서 알아보도록 하겠습니다. 1. 정의 : 부분 공간(Subspace) $V$를 체 $\mathbf{F}$ 상의 벡터 공간($V.S/
everyday-image-processing.tistory.com
$N(T)$가 $V$의 부분공간임을 증명하기 위해서는 $\mathbf{0} \in N(T)$와 $\mathbf{u}_{1}, \mathbf{u}_{2} \in N(T)$ 그리고 $c \in \mathbf{F}$에 대해서 $\mathbf{u}_{1} + \mathbf{u}_{2}, c\mathbf{u}_{1} \in N(T)$을 보여야한다.
1). 정리1에 의해서 $V$의 항등원 $\mathbf{0}_{V}$에 대한 선형변환은 $W$의 항등원이므로 $T(\mathbf{0}_{V}) = \mathbf{0}_{W}$와 같이 쓸 수 있다. 영 공간의 정의에 의해서 $\mathbf{0}_{V} \in N(T)$이다.
2). $T(\mathbf{u}_{1} + \mathbf{u}_{2}) = T(\mathbf{u}_{1}) + T(\mathbf{u}_{2}) = \mathbf{0} + \mathbf{0} = \mathbf{0} \Rightarrow \mathbf{u}_{1} + \mathbf{u}_{2} \in N(T)$
3). $T(c\mathbf{u}_{1}) = cT(\mathbf{u}_{1}) = c \cdot \mathbf{0} = \mathbf{0} \Rightarrow c\mathbf{u}_{1} \in N(T)$
다음으로 $R(T)$가 $W$의 부분공간임을 증명하기 위해서는 $\mathbf{0} \in R(T)$와 $T(\mathbf{u}_{1}), T(\mathbf{u}_{2}) \in R(T)$ 그리고 $c \in \mathbf{F}$에 대해서 $T(\mathbf{u}_{1}) + T(\mathbf{u}_{2}), cT(\mathbf{u}_{1}) \in R(T)$을 보여야한다.
1). 정리1에 의해서 $V$의 항등원 $\mathbf{0}_{V}$에 대한 선형변환은 $W$의 항등원이므로 $T(\mathbf{0}_{V}) = \mathbf{0}_{W}$와 같이 쓸 수 있다. 치역의 정의에 의해서 $\mathbf{0}_{W} \in R(T)$이다.
2). $T(\mathbf{u}_{1}) + T(\mathbf{u}_{2}) = T(\mathbf{u}_{1} + \mathbf{u}_{2}) \in R(T)$
3). $cT(\mathbf{u}_{1}) = T(c\mathbf{u}_{1}) \in R(T)$
따라서, 정리1은 증명된다.
정리2.
어떤 체 $\mathbf{F}$에 대한 벡터공간 $V$와 $W$와 선형변환 $T : V \rightarrow W$가 주어졌다고 하자. 만약 $\beta = \{u_{1}, \dots, u_{n}\}$이 $V$의 기저라고 할 때, $T$의 치역공간은 아래와 같다.
$$R(T) = \text{span}(T(\beta)) = \text{span}(\{T(u_{1}), \dots, T(u_{n})\})$$
증명
기본적으로 정리2는 $R(T) = \text{span}(T(\beta))$임을 증명해야합니다. 이는 본질적으로 두 집합 사이의 포함관계를 이용해서 증명해야하기 때문에 $R(T) \subseteq \text{span}(T(\beta))$와 $\text{span}(T(\beta)) \subseteq R(T)$ 모두 보여야합니다.
1). $\text{span}(T(\beta)) \subseteq R(T)$ : 선형변환의 정의에 의해 자명하게 모든 $i = 1, \dots, n$에 대해서 $T(u_{i}) \in W$가 성립한다. 즉, $\{T(u_{1}), \dots, T(u_{n})\} \subset R(T)$이다. 이는 선형대수학 - 선형결합의 정리2에 의해 $\text{span}(\{T(u_{1}), \dots, T(u_{n})\}) = \text{span}(T(\beta)) \subseteq R(T)$이다.
2). $\text{span}(T(\beta)) \subseteq R(T)$ : 임의의 벡터 $w \in R(T)$를 선택한다. 그러면 어떤 벡터 $u \in V$에 대해서 $T(u) = v$를 만족한다. 여기서, $\beta$는 벡터공간 $V$의 기저이기 때문에 어떤 스칼라 $a_{1}, \dots, a_{n} \in \mathbf{F}$에 대해서 벡터 $u$를 기저의 선형결합으로 표현할 수 있다.
$$u = a_{1}u_{1} + \cdots + a_{n}u_{n} = \sum_{i = 1}^{n} a_{i}u_{i}$$
여기서, $T$가 선형이기 때문에 양변에 $T$를 취한 뒤 선형성을 이용해서 정리할 수 있다.
$$w = T(u) = T(\sum_{i = 1}^{n} a_{i}u_{i}) = \sum_{i = 1}^{n} a_{i} T(u_{i})$$
즉, $w$는 벡터 $\{T(u_{1}), \dots, T(u_{n})\}$의 선형결합이기 때문에 $w \in \text{span}(T(\beta))$이다.
저희는 정리2를 이용해서 $V$의 기저만 찾을 수 있면 $R(T)$의 기저도 쉽게 찾을 수 있습니다. 예를 들어, $T : P_{2}(\mathbb{R}) \rightarrow M_{2 \times 2}(\mathbb{R})$이 아래와 같이 정의되었다고 하겠습니다.
$$T(f(x)) = \begin{bmatrix} f(1) - f(2) & 0 \\ 0 & f(0) \end{bmatrix}$$
여기서, $P_{2}(\mathbb{R})$의 기저는 $\beta = \{1, x, x^{2}\}$으로 쉽게 알 수 있습니다. 이제 각 기저에 대해서 선형변환 $T$를 적용한 뒤 선형생성을 적용하면 정리2에 의해 $R(T)$를 찾을 수 있습니다.
$$\begin{align*} R(T) &= \text{span}(T(\beta)) = \text{span}(\{T(1), T(x), T(x^{2})\}) \\ &= \text{span}(\{\begin{bmatrix} 0 & 0 \\ 0 & 1 \end{bmatrix}, \begin{bmatrix} -1 & 0 \\ 0 & 0 \end{bmatrix}, \begin{bmatrix} -3 & 0 \\ 0 & 0 \end{bmatrix}\}) \\ &= \text{span}(\{\begin{bmatrix} 0 & 0 \\ 0 & 1 \end{bmatrix}, \begin{bmatrix} -1 & 0 \\ 0 & 0 \end{bmatrix}\})\end{align*}$$
따라서, $R(T)$의 기저는 $\{\begin{bmatrix} 0 & 0 \\ 0 & -1 \end{bmatrix}, \begin{bmatrix} -1 & 0 \\ 0 & 0 \end{bmatrix}\}$임을 알 수 있습니다.
정의4. 영공간의 차원 (nullity)과 치역공간의 차원 (rank)
어떤 체 $\mathbf{F}$에 대한 벡터공간 $V$와 $W$가 주어졌을 때, $T : V \rightarrow W$이 선형이라고 하자. 만약, $N(T)$와 $R(T)$가 유한차원이라면 $T$의 영공간 $N(T)$의 차원 $\text{nullity}(T) = \text{dim}(N(T))$와 치역공간 $R(T)$의 차원 $\text{rank}(T) = \text{dim}(R(T))$을 각각 정의할 수 있다.
Let $V$, and $W$ be vector spaces over a field $\mathbf{F}$, and let $T : V \rightarrow W$ be linear. If $N(T)$ and $R(T)$ are finite-dimensional, then we define the nullity of $T$, and the rank of $T$ to be the dimensions of $N(T)$ and $R(T)$, respectively. Namely, $\text{nullity}(T) = \text{dim}(N(T))$ and $\text{rank}(T) = \text{dim}(R(T))$.
정리3. 차원정리 (Dimension Theorem)
어떤 체 $\mathbf{F}$에 대한 벡터공간 $V$와 $W$가 주어졌을 때, $T : V \rightarrow W$을 선형변환, $\text{dim}(V) < \infty$라고 하자. 그러면 $V$의 차원은 영 공간 $N(T)$의 차원과 치역 $R(T)$의 차원의 합과 동일하다.
$$\text{dim}(V) = \text{nullity}(T) + \text{rank}(T)$$
증명
차원정리는 선형대수학에서 Replacement Theorem만큼 중요한 정리로 앞으로 굉장히 자주 사용되는 정리이기 때문에 꼭 숙지하셔야합니다. 차원정리의 증명은 벡터공간 $V$의 기저에서 영공간 $N(T)$의 기저를 제외한 벡터들이 $R(T)$의 기저임을 증명하는 것으로 이루어집니다. 기저를 증명한다는 것은 기저의 정의를 만족하는 지 보여야한다는 것이겠죠? 따라서, 선형대수학 - 기저와 차원의 정의1. 기저 (basis)를 꼭 숙지하고 오시길 바랍니다.
$\text{dim}(V) = n$ 그리고 $\text{nullity}(T) = k$라고 하자. 또한, $\gamma = \{u_{1}, \dots, u_{k}\}$를 $T$의 영공간 $N(T)$의 기저라고 하자. 이때, 정리1에 의해 $N(T) < V$이기 때문에 선형대수학 - 기저와 차원의 따름정리4-1로 인해서 $\gamma$는 벡터공간 $V$의 기저 $\beta$로 확장가능하므로 $\gamma \subset \beta = \{u_{1}, \dots, u_{k}, u_{k + 1}, \dots, u_{n}\}$이다. 이때, 우리는 $\gamma$를 제외한 나머지 벡터들의 선형변환이 $S = \{T(u_{k + 1}), \dots, T(u_{n})\}$이 치역공간 $R(T)$의 기저임을 보이면 된다.
1). $\text{span}(S) = R(T)$ : 여기서 정리2에 의해서 $R(T) = \text{span}(T(\beta)) = \text{span}(\{T(u_{1}), \dots, T(u_{n})\})$이다. 그런데, $u_{1}, \dots, u_{k} \in N(T)$이므로 $T(u_{1}) = \cdots = T(u_{k}) = 0$이다. 따라서, 우리는 $R(T)$를 아래와 같이 정리할 수 있다.
$$\begin{align*} R(T) &= \text{span}(T(\beta)) = \text{span}(\{T(u_{1}), \dots, T(u_{n})\}) \\ &= \text{span}(\{T(u_{k + 1}, \dots, T(u_{n}))\}) = \text{span}(S) \end{align*}$$
2). $S$는 선형독립이다 : 어떤 $b_{k + 1}, \dots, b_{n} \in \mathbf{F}$에 대해서 $\sum_{i = k + 1}^{n} b_{i}u_{i} = \mathbf{0}$이라고 하자. 이때, $T$가 선형이므로 양변에 $T$를 취하면 아래와 같이 정리할 수 있다.
$$\sum_{i = k + 1}^{n} b_{i}T(u_{i}) = T\left( \sum_{i = k + 1}^{n} b_{i}u_{i} \right) = \mathbf{0}$$
즉, $\sum_{i = k + 1}^{n} b_{i}u_{i} \in N(T)$이다. 이는 $\sum_{i = k + 1}^{n} b_{i}u_{i} = \sum_{i = 1}^{k} c_{i}u_{i}$를 만족하는 계수 $c_{1}, \dots, c_{k} \in \mathbf{F}$가 존재한다는 의미이다. 따라서, $\sum_{i = 1}^{n} (-c_{i})u_{i} + \sum_{i = k + 1}^{n} b_{i}u_{i} = \mathbf{0}$이라고 쓸 수 있다.
여기서, $\beta$는 $V$의 기저이므로 선형독립이다. 따라서, $\sum_{i = 1}^{n} (-c_{i})u_{i} + \sum_{i = k + 1}^{n} b_{i}u_{i} = \mathbf{0}$를 만족하는 계수쌍은 0밖에 없으므로 $b_{k + 1} = \cdots = b_{n} = 0$이다. 따라서, $S$도 선형독립이다.
1)과 2)에 의해 집합 $S$는 $R(T)$의 계수로 $\text{rank}(T) = n - k$이다. 따라서, $\text{nullity}(T) + \text{rank}(T) = n = \text{dim}(V)$가 성립한다.
저희는 지금까지 선형변환의 정의와 관련된 다양한 정리들을 알아보았습니다. 함수에도 단사함수, 전사함수, 전단사함수가 있듯이 선형변환 역시 단사변환, 전사변환, 전단사변환이 존재합니다. 이번에는 어떤 조건을 만족해야 선형변환이 어떤 변환에 속하는 지 알아보도록 하겠습니다.
정리4.
어떤 체 $\mathbf{F}$에 대한 벡터공간 $V$와 $W$가 주어졌을 때, $T : V \rightarrow W$을 선형변환이라고 하자. 그러면 $T$가 단사변환인 것은 $N(T) = \{0\}$인 것과 동치이다.
증명
1). $(\Rightarrow)$ : $T$가 단사변환이라고 하자. 임의의 $\mathbf{x} \in N(T)$를 선택하자. 그러면 영공간의 정의에 의해 $T(\mathbf{x}) = \mathbf{0}$이다. 또한, Remark1에서 $T(\mathbf{0}) = \mathbf{0}$이므로 $T(\mathbf{x}) = T(\mathbf{0})$이라고 쓸 수 있다. 여기서 $T$가 단사변환이라고 가정하였으므로 $\mathbf{x} = \mathbf{0}$이다. 따라서, $N(T) = \{\mathbf{0}\}$이다.
2). $(\Leftarrow)$ : $N(T) = \{\mathbf{0}\}$이라고 하자. 그리고 $T(\mathbf{x}) = T(\mathbf{y})$를 만족하는 두 벡터 $\mathbf{x}, \mathbf{y} \in V$를 선택하자. 그러면 $T$의 선형성에 의해서 $\mathbf{0} = T(\mathbf{x}) - T(\mathbf{y}) = T(\mathbf{x} - \mathbf{y})$이다. 따라서, 영공간의 정의에 의해 $\mathbf{x} - \mathbf{y} \in N(T)$이다. 영공간에는 유일하게 영벡터 $\mathbf{0}$만 존재하므로 $\mathbf{x} - \mathbf{y} = \mathbf{0}$이다. 결론적으로 $\mathbf{x} = \mathbf{y}$이다. 즉, $T$는 단사함수이다.
1)과 2)에 의해 두 명제는 서로 동치이다.
정리5.
어떤 체 $\mathbf{F}$에 대한 동일한 차원의 벡터공간 $V$와 $W$가 주어졌을 때, $T : V \rightarrow W$을 선형변환이라고 하자. 그러면 아래의 3개의 명제는 동치이다.
(a). $T$가 단사변환이다.
(b). $T$가 전사변환이다.
(c). $\text{rank}(T) = \text{dim}(V)$
증명
정리4에서는 단사변환에 대한 이야기만 알 수 있지만, 정리5에서는 전사변환도 보일 수 있습니다. 예를 들어 $T$가 단사변환이면서 $\text{rank}(T) = \text{dim}(V)$를 만족하게 되면 $T$는 정리5에 의해 전사변환이라는 결과도 얻을 수 있습니다.
$T$가 단사변환이라고 가정하자 ((a) 가정). 정리4에 의해 $T$가 단사변환이기 위해서는 $N(T) = \{\mathbf{0}\}$인 것과 동치임을 알게 되었다. 여기서 $N(T)$의 기저는 $\emptyset$이므로 $\text{nullity}(T) = 0$이다. 여기서 차원정리에 의해 $\text{nullity}(T) + \text{rank}(T) = \text{dim}(V)$이므로 $\text{rank}(T) = \text{dim}(V)$이다 ((c) 증명). 이때, 두 벡터공간 $V$와 $W$의 차원이 동일하므로 $\text{rank}(T) = \text{dim}(W)$이다. $\text{rank}(T)$의 정의에 의해 $\text{dim}(R(T)) = \text{dim}(V)$라고 쓸 수 있으므로 선형대수학 - 기저와 차원의 정리4에 의해 $R(T) = W$이다. 이는 전사변환의 정의이므로 $T$는 전사변환이다.
간단하게 예를 들어보도록 하겠습니다. $T : P_{2}(\mathbb{R}) \rightarrow P_{3}(\mathbb{R})$이 아래와 같이 정의된다고 하겠습니다.
$$T(f(x)) = \int_{0}^{x} 3f(t) \; dt + f^{'}(x)$$
여기서, $P_{2}(\mathbb{R})$의 기저는 $\beta = \{1, x, x^{2}\}$입니다. 따라서, 정리2에 의해서 $R(T)$를 구할 수 있죠.
$$\begin{align*} R(T) &= \text{span}(T(\beta)) = \text{span}(\{T(1), T(x), T(x^{2})\}) \\ &= \text{span}(\{3x, 2 + \frac{3}{2}x^{2}, 4x + x^{3}\})\end{align*}$$
이때, $S = \{3x, 2 + \frac{3}{2}x^{2}, 4x + x^{3}\}$이 선형독립임을 보이기 위해 $a_{1}, a_{2}, a_{3} \in \mathbb{R}$를 선택하도록 하겠습니다. 그리고 $S$의 선형결합이 0인 계수쌍이 0밖에 없음을 보이면 됩니다.
$$\begin{align*} 3a_{1}x + (2 + \frac{3}{2}x^{2})a_{2} + (4x + x^{3})a_{3} &= a_{3}x^{3} + \frac{3}{2}a_{2}x^{2} + (3a_{1} + 4a_{3})x + 2a_{2} = \mathbf{0} \end{align*}$$
위 식에서 저희는 아래의 연립방정식을 얻을 수 있습니다.
$$\begin{cases} a_{3} &= 0 \\ a_{2} &= 0 \\ 3a_{1} + 4a_{3} &= 0 \\ 2a_{2} &= 0 \end{cases}$$
위 연립방정식을 만족하는 해는 오직 $a_{1} = a_{2} = a_{3} = a_{4} = 0$이므로 $S$는 선형독립입니다. 따라서, $\text{rank}(T) = 3$이죠. 여기서, 차원정리를 적용하면 $\text{nullity}(T) + \text{rank}(T) = \text{dim}(P_{2}(\mathbb{R})) = 3$이므로 $\text{nullity}(T) = 0$입니다. 이는 정리4에 의해서 $T$가 단사변환임을 알 수 있죠. 하지만!! 전사변환은 아닙니다. 왜냐하면 정리5의 가정은 두 벡터공간 $V$와 $W$의 차원이 동일해야한다고 했지만 $\text{dim}(P_{2}(\mathbb{R})) = 3 \neq 4 = \text{dim}(P_{3}(\mathbb{R}))$이기 때문이죠. 실제로 전사함수가 되려면 $\text{rank}(T) \neq \text{dim}(P_{3}(\mathbb{R}))$이기 때문에 전사함수가 아니죠.
자 그렇다면 다음으로 생각해볼 것은 두 선형변환이 있을 때 어떤 경우에 "같다"라고 말할 수 있을까요? 선형대수학 - 기저와 차원의 정리4에서는 두 벡터공간이 같기 위한 몇 가지 조건을 명시하고 있습니다. 선형변환에서도 "같다"라는 개념을 적용할 수 있습니다.
정리6.
어떤 체 $\mathbf{F}$에 대한 벡터공간 $V$와 $W$가 주어졌을 때, $T : V \rightarrow W$을 선형변환이라고 하자. 그리고 $\{u_{1}, \dots, u_{n}\}$이 $V$의 기저라고 하자. $w_{1}, \dots, w_{n} \in W$에 대해서 $i = 1, \dots, n$일 때 $T(u_{i}) = w_{i}$를 만족하는 선형변환 $T : V \rightarrow W$는 유일하다.
증명
정리6의 증명은 2개의 단계로 이루어집니다. 먼저, $T$가 선형변환이라는 것과 유일하다는 것 두 가지를 모두 증명해야하죠.
먼저, $\mathbf{x} \in V$인 벡터 $x$를 선택한다. 그러면 $\mathbf{x}$는 $V$의 기저에 대한 계수 $a_{1}, \dots, a_{n} \in \mathbf{F}$가 주어졌을 때 선형결합으로 표현할 수 있다.
$$\mathbf{x} = \sum_{i = 1}^{n} a_{i}u_{i}$$
이때, 선형변환 $T : V \rightarrow W$를 $T(\mathbf{x}) = \sum_{i = 1}^{n} a_{i}w_{i}$로 정의하자.
1). $T$는 선형변환이다 : 두 벡터 $u, v \in V$와 스칼라 $d \in \mathbf{F}$를 선택하자. 그러면 $u$와 $v$를 $V$의 기저의 선형결합으로 표현할 수 있다.
$$u = \sum_{i = 1}^{n} b_{i}u_{i}$$
$$v = \sum_{i = 1}^{n} c_{i}u_{i}$$
따라서, $du + v = d \left( \sum_{i = 1}^{n} b_{i}u_{i} \right) + \sum_{i = 1}^{n} c_{i}u_{i} = \sum_{i = 1}^{n} (db_{i} + c_{i})u_{i}$이다. 이제 여기서 변환 $T$를 적용한다.
$$T(du + v) = \sum_{i = 1}^{n} (db_{i} + c_{i})w_{i} = d\sum_{i = 1}^{n} b_{i}w_{i} + \sum_{i = 1}^{n} c_{i}w_{i} = dT(u) + T(v)$$
따라서, $T$는 선형변환이다.
2). $T$는 유일하다 : $U : V \rightarrow W$가 선형변환이고 $i = 1, \dots, n$에 대해서 $U(u_{i}) = w_{i}$를 만족한다고 하자. 그러면 $\mathbf{x} \in V$에 대해서 $\mathbf{x} = \sum_{i = 1}^{n} a_{i}u_{i}$ 이므로 아래와 같이 식을 정리할 수 있다.
$$\begin{align*} U(\mathbf{x}) &= U(\sum_{i = 1}^{n} a_{i}u_{i}) \\ &= \sum_{i = 1}^{n} a_{i}U(u_{i}) \\ &= \sum_{i = 1}^{n} a_{i}w_{i} \\ &= \sum_{i = 1}^{n} a_{i}T(u_{i}) \\ &= T(\sum_{i = 1}^{n} a_{i}u_{i}) = T(\mathbf{x}) \end{align*}$$
따라서, $U = T$이다.
따름정리6-1.
어떤 체 $\mathbf{F}$에 대한 벡터공간 $V$와 $W$가 주어졌을 때, $V$가 유한개의 기저 $\{u_{1}, \dots, u_{n}\}$을 가진다고 하자. 그리고 $T, U : V \rightarrow W$가 선형이고 $i = 1, \dots, n$에 대해서 $T(u_{i}) = U(u_{i})$를 만족하면 $U = T$이다.
설명
따름정리6-1이 처음에 제가 말씀드렸던 두 선형변환의 일치성에 대해서 말하고 있습니다. 쉽게 말해 정의역의 역할을 하는 벡터공간 $V$의 기저들만 선형변환을 적용해서 동일한 결과가 나오면 두 선형변환은 같다고 할 수 있다는 것이죠.
참고문헌
Linear Algebra (Stephan. H)
'수학 > 선형대수학' 카테고리의 다른 글
| 선형대수학 - 선형변환 합성과 행렬곱 (0) | 2021.11.05 |
|---|---|
| 선형대수학 - 선형변환의 행렬표현 (1) | 2021.11.03 |
| 선형대수학 - 기저와 차원 (0) | 2021.10.28 |
| 선형대수학 - 선형 종속과 독립 (0) | 2021.10.26 |
| 선형대수학 - 선형 결합 (0) | 2021.10.25 |
