안녕하세요. 지난 포스팅의 디지털 영상 처리 - 의사 칼라 영상 처리에서는 시각화를 위한 칼라 처리에 대해서 알아보았습니다. 오늘은 각 칼라 요소가 8비트씩 표현되는 풀-칼라 영상에 적용할 수 있는 처리 기법들에 대해서 알아보도록 하겠습니다.
풀-칼라 영상에서의 처리는 크게 2가지로 분류할 수 있습니다. 첫번째 방법인 칼라 성분별 처리는 각 성분 영상을 개별적으로 처리하고 개별적으로 처리된 성분 영상을 합쳐서 칼라 영상을 보여주는 방식입니다. 예를 들어서 RGB 칼라 공간의 경우에는 R, G, B에 대해서 각각 서로 다른 처리를 하거나 특정 칼라 성분만 처리를 하여 다시 RGB로 합치는 것입니다. 두번째 방법인 벡터-기반 처리는 칼라 화소를 직접 활용하는 방법입니다. 예를 들어 첫번째 방법은 각 성분 영상이기 때문에 그레이 스케일에서의 처리입니다. 하지만, 두번째 방법은 RGB를 같이 활용하기 때문에 하나의 벡터 $<r, g, b>$를 함께 처리하는 것입니다.
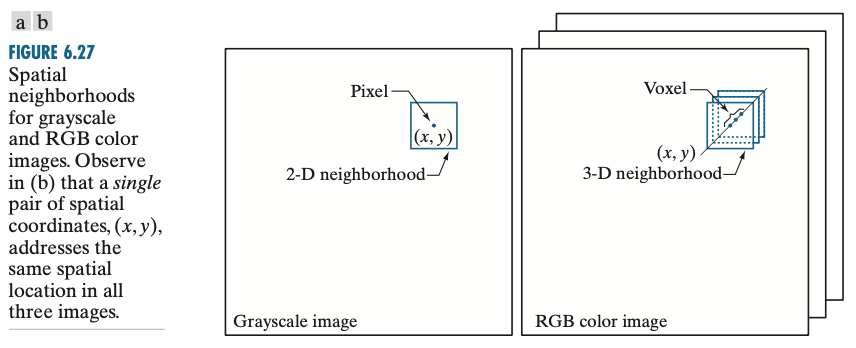
위에서 왼쪽 그림과 같이 그레이 스케일에서 각각 처리하는 것이 첫번째 방법, 오른쪽 그림과 같이 RGB 칼라 공간을 직접적으로 처리하여 결국에는 벡터를 다루는 것이 두번째 방법입니다. 앞으로 저희는 이 벡터를 $\mathbf{c}$라고 하겠습니다.
$$\mathbf{c} = \begin{bmatrix} c_{R} \\ c_{G} \\ c_{B} \end{bmatrix} = \begin{bmatrix} R \\ G \\ B \end{bmatrix}$$
위 식은 임의의 RGB 칼라 공간에서 임의의 벡터를 의미하고 아래와 같이 표현할 수도 있습니다.
$$\mathbf{c} = \begin{bmatrix} c_{R}(x, y) \\ c_{G}(x, y) \\ c_{B}(x, y) \end{bmatrix} = \begin{bmatrix} R(x, y) \\ G(x, y) \\ B(x, y) \end{bmatrix}$$
영상의 크기가 $M \times N$이라면 $\mathbf{c}(x, y)$는 총 $MN$ 개의 벡터가 존재하고 $x = 0 \sim M -1$, $y = 0 \sim N - 1$입니다. 위에서 언급한 칼라 성분별 처리와 벡터-기반 처리는 항상 동일한 결과를 보여주지 않습니다. 두 처리 결과가 동일하기 위해서는 2개의 조건이 만족해야합니다.
- 두 처리가 벡터와 스칼라에 모두 적용 가능해야한다.
- 벡터의 각 요소에 대한 연산이 나머지 요소들과 독립적이여야한다.
이 부분은 다음 포스팅에서 같은 경우와 같이 않은 경우 모두 보여드리도록 하겠습니다.
'image processing' 카테고리의 다른 글
| 디지털 영상 처리 - 스무딩과 샤프닝 (0) | 2021.07.23 |
|---|---|
| 디지털 영상 처리 - 칼라 변환 (0) | 2021.07.19 |
| 디지털 영상 처리 - 의사 칼라 영상 처리 (0) | 2021.07.16 |
| 디지털 영상 처리 - 칼라 기초 (0) | 2021.07.12 |
| 디지털 영상 처리 - 투영에 의한 영상 재구성 2 (1) | 2021.07.11 |
안녕하세요. 지난 포스팅의 디지털 영상 처리 - 의사 칼라 영상 처리에서는 시각화를 위한 칼라 처리에 대해서 알아보았습니다. 오늘은 각 칼라 요소가 8비트씩 표현되는 풀-칼라 영상에 적용할 수 있는 처리 기법들에 대해서 알아보도록 하겠습니다.
풀-칼라 영상에서의 처리는 크게 2가지로 분류할 수 있습니다. 첫번째 방법인 칼라 성분별 처리는 각 성분 영상을 개별적으로 처리하고 개별적으로 처리된 성분 영상을 합쳐서 칼라 영상을 보여주는 방식입니다. 예를 들어서 RGB 칼라 공간의 경우에는 R, G, B에 대해서 각각 서로 다른 처리를 하거나 특정 칼라 성분만 처리를 하여 다시 RGB로 합치는 것입니다. 두번째 방법인 벡터-기반 처리는 칼라 화소를 직접 활용하는 방법입니다. 예를 들어 첫번째 방법은 각 성분 영상이기 때문에 그레이 스케일에서의 처리입니다. 하지만, 두번째 방법은 RGB를 같이 활용하기 때문에 하나의 벡터 $<r, g, b>$를 함께 처리하는 것입니다.

위에서 왼쪽 그림과 같이 그레이 스케일에서 각각 처리하는 것이 첫번째 방법, 오른쪽 그림과 같이 RGB 칼라 공간을 직접적으로 처리하여 결국에는 벡터를 다루는 것이 두번째 방법입니다. 앞으로 저희는 이 벡터를 $\mathbf{c}$라고 하겠습니다.
$$\mathbf{c} = \begin{bmatrix} c_{R} \\ c_{G} \\ c_{B} \end{bmatrix} = \begin{bmatrix} R \\ G \\ B \end{bmatrix}$$
위 식은 임의의 RGB 칼라 공간에서 임의의 벡터를 의미하고 아래와 같이 표현할 수도 있습니다.
$$\mathbf{c} = \begin{bmatrix} c_{R}(x, y) \\ c_{G}(x, y) \\ c_{B}(x, y) \end{bmatrix} = \begin{bmatrix} R(x, y) \\ G(x, y) \\ B(x, y) \end{bmatrix}$$
영상의 크기가 $M \times N$이라면 $\mathbf{c}(x, y)$는 총 $MN$ 개의 벡터가 존재하고 $x = 0 \sim M -1$, $y = 0 \sim N - 1$입니다. 위에서 언급한 칼라 성분별 처리와 벡터-기반 처리는 항상 동일한 결과를 보여주지 않습니다. 두 처리 결과가 동일하기 위해서는 2개의 조건이 만족해야합니다.
- 두 처리가 벡터와 스칼라에 모두 적용 가능해야한다.
- 벡터의 각 요소에 대한 연산이 나머지 요소들과 독립적이여야한다.
이 부분은 다음 포스팅에서 같은 경우와 같이 않은 경우 모두 보여드리도록 하겠습니다.
'image processing' 카테고리의 다른 글
| 디지털 영상 처리 - 스무딩과 샤프닝 (0) | 2021.07.23 |
|---|---|
| 디지털 영상 처리 - 칼라 변환 (0) | 2021.07.19 |
| 디지털 영상 처리 - 의사 칼라 영상 처리 (0) | 2021.07.16 |
| 디지털 영상 처리 - 칼라 기초 (0) | 2021.07.12 |
| 디지털 영상 처리 - 투영에 의한 영상 재구성 2 (1) | 2021.07.11 |
