안녕하세요. 지난 포스팅의 디지털 영상 처리 - 노이즈만 있을 때의 복원(공간 필터링) : 평균 필터와 순서-통계 필터 구현에 대해서 알아보았습니다. 실제 MATLAB으로도 구현을 해보고 각 노이즈별로 어떤 공간 필터링이 효과가 있는 지 까지 분석을 진행하였습니다. 지금까지는 영상 공간에서 수행하는 필터링이였다면 이번에는 주파수 공간에서 수행하는 필터링에 대해서 알아보도록 하겠습니다. 기본적으로 저희가 이전에 알아보았던 공간 필터링과 큰 차이가 없기 때문에 혹시 아직 보시지 않았다면 제가 이전에 미리 정리해놓은 주파수 공간 필터링과 관련된 내용을 먼저 숙지하고 오신 뒤에 보시는 것을 추천드립니다.
1. 노치 필터(Notch Filter)
이 부분은 기본적으로 제가 미리 설명드린 아래의 링크를 보시면 쉽게 이해할 수 있습니다. 이 부분에 대한 수학적인 설명은 아래의 링크에 자세히 설명해놓았으니 꼭 참고해보시길 바랍니다.
디지털 영상 처리 - 선택적 필터링
안녕하세요. 지난 포스팅의 디지털 영상 처리 - 주파수 도메인을 이용한 영상 샤프닝에 이어서 오늘은 선택적 필터링(selective filtering)에 대해서 알아보겠습니다. 선택적 필터링은 크게 3가지로
everyday-image-processing.tistory.com
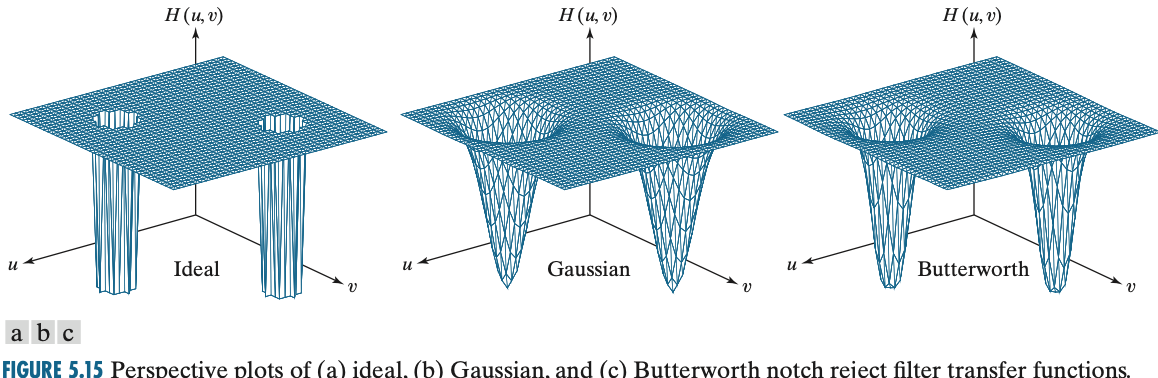
또한 저희가 주파수 도메인의 특성에 대해서 알아보았습니다. 그 결과 원점에 대한 대칭성이 존재한다는 것까지 알았죠. 따라서 저희는 필터링을 수행할 때 위의 그림과 같이 한 지점만 수행하는 것이 아니라 원점에 대칭인 지점까지 필터링을 해주면 됩니다. 간단한 예시 그림을 통해 알아보도록 하겠습니다.

위 그림은 우상향 대각선의 주기적 노이즈에 의해 오염된 영상을 보여주고 있습니다. 이 영상을 주파수 공간으로 변환하면 우측 상단 영상의 화살표가 가르키는 지점과 같이 어떤 부자연스러운 두 개의 점이 빛나고 있음을 볼 수 있습니다. 따라서 이러한 지점을 "경험적"으로 노이즈라고 판단하고 좌표를 얻은 후 해당 지점들을 차단하면 우측 하단 영상과 같이 아주 깔끔한 영상을 얻을 수 있습니다. 제가 여기서 한 가지 강조하고 싶은 것은 바로 "경험적"으로 차단했다는 것입니다. 과연 두 개의 점들이 정말로 노이즈를 의미할까요? 다른 영상에서는 어떨까요? 이러한 직관을 얻는 방법은 다양한 노이즈에 오염된 영상을 보고 판단할수 밖에 없습니다. 그리고 얼마나 차단할지도 결정해주어야하겠죠? 이 경우 역시 실험과 실패를 반복하며 그나마 좋은 결과를 보여주는 파라미터를 사용할 수 밖에 없습니다.

위 영상은 방금 차단한 필터를 역으로 통과시켜서 해당 노이즈만 추출한 결과입니다. 저희의 예상대로 아주 잘 추출이 된 것을 관찰할 수 있습니다.
2. 최적 노치 필터링(Optimum Notch Filtering)
여기서 최적이라는 의미는 노치 필터링을 통해 복원된 영상 $\hat{f}(x, y)$의 지역적 분산을 최소화시킨다는 의미입니다. 알고리즘 자체는 간단하기 때문에 쉽게 이해할 수 있습니다. 가장 먼저 해야할 것은 간섭 패턴의 주요 주파수 성분들을 빼는 것입니다. 즉, 저희가 미리 정의한 노치 통과 필터 $H_{\text{NP}}(\mu, \nu)$를 각 스파이크 성분에 위치 시켜서 간섭 패턴과 연관된 성분들만 통과시키도록 만들어주어야합니다. 노이즈로 오염된 영상의 푸리에 변환을 $G(\mu, \nu)$라고 했을 때 위의 과정을 아래와 같이 작성할 수 있습니다.
$$N(\mu, \nu) = H_{\text{NP}}(\mu, \nu)G(\mu, \nu)$$
하지만 여기서 노치 통과 필터 $H_{\text{NP}}(\mu, nu)$를 만들 때 주파수 공간에서 어떤 것이 간섭 스파이크인지 신중하게 판단해야합니다. 이 과정은 어쩔 수 없이 $G(\mu, \nu)$ 내에서 발생한 스파이크를 관찰 및 제거를 반복적으로 수행하여 이루어져야만 합니다. 이 과정을 통해 특정 스파이크를 빼는 노치 통과 필터 $H_{\text{NP}}(\mu, nu)$를 결정했다고 가정하면 노이즈는 영상 공간에서 아래와 같이 얻을 수 있습니다.
$$\eta(x, y) = \mathcal{F}^{-1}\{H_{\text{NP}}(\mu, \nu)G(\mu, \nu)\}$$
여기서 다시 문제는 2가지로 나뉩니다. 먼저, $\eta(x, y)$를 저희가 이미 알고 있다면 오염된 영상은 오염되지 않은 영상에 노이즈 $\eta(x, y)$ 사이의 합으로 얻어지기 때문에 $g(x, y) - \eta(x, y)$를 통해서 쉽게 영상을 복원할 수 있습니다. 하지만 저희는 일반적으로 $\eta(x, y)$에 대한 정보가 한정적이기 때문에 위와 같은 방법은 사용하지 못합니다. 따라서 저희는 $\eta(x, y)$를 실제 오염 노이즈 $\eta_{\text{true}}(x, y)$의 근사된 버전이라고 생각하도록 하겠습니다. 여기서 저희는 추정된 노이즈와 실제 노이즈 사이의 차이를 보정해주는 가중치 함수 $w(x, y)$를 도입하여 아래와 같이 모델링하도록 하겠습니다.
$$\hat{f}(x, y) = g(x, y) - w(x, y)\eta(x, y)$$
여기서 $w(x, y)$는 가중(weighting) 또는 변조(modulation) 함수라고 부릅니다. 여기서 성공적인 영상 복원을 위해서는 $w(x, y)$를 잘 선택하면 됩니다. 영상 내의 작은 지점에서의 분산이 크다는 것은 노이즈가 강하다는 것을 의미하기 때문에 이를 활용하여 $w(x, y)$를 적용했을 때 복원된 영상의 지역적 분산을 최소화시키는 방향으로 결정하면 됩니다. 이 부분까지 이해하시면 대부분 이해하신 겁니다. 나머지는 $w(x, y)$만 모델링하면 됩니다.
일단 복원된 영상 $\hat{f}(x, y)$ 내에서 $m \times n$ 크기의 중심이 $(x, y)$인 이웃 $S_{xy}$을 생각해보도록 하겠습니다. 해당 지역적 분산은 이웃 내의 샘플들을 이용하여 추정할 수 있습니다.
$$\sigma^{2}(x, y) = \frac{1}{mn}\sum_{(r, c) \in S_{xy}}\left[\hat{f}(r, c) - \bar{\hat{f}}\right]^{2}$$
그리고 $\bar{\hat{f}}$는 해당 이웃의 평균값을 의미합니다.
$$\bar{\hat{f}} = \frac{1}{mn}\sum_{(r, c) \in S_{xy}} \hat{f}(r, c)$$
이때, $\sigma^{2}(x, y)$에 $\hat{f}(x, y) = g(x, y) - w(x, y)\eta(x, y)$를 대입해보도록 하겠습니다.
$$\sigma^{2}(x, y) = \frac{1}{mn}\sum_{(r, c) \in S_{xy}}\{\left[g(r, c) - w(r, c)\eta(r, c)\right] - \left[\bar{g} - \bar{w\eta}\right]\}^{2}$$
여기서 $\bar{g}$와 $\bar{w\eta}$는 각각 이웃 $S_{xy}$ 내의 평균값을 의미합니다. 여기서 $w$가 $S_{xy}$에서는 일정한 값을 가진다고 가정하면 $w(r, c) = w(x, y)$라고 볼 수 있습니다. 여기서 $(x, y)$는 이웃 $S_{xy}$의 중심 픽셀을 의미하죠. 따라서 사실상 $w(x, y)$는 단순한 상수가 되기 때문에 $\bar{w\eta} = w(x, y)\bar{\eta}$로 바뀝니다. 이러한 가정을 가지고 다시 한번 $\sigma^{2}$을 정리하면 아래와 같이 쓸 수 있습니다.
$$\sigma^{2}(x, y) = \frac{1}{mn}\sum_{(r, c) \in S_{xy}}\{\left[g(r, c) - w(r, c)\eta(r, c)\right] - \left[\bar{g} - w(x, y)\bar{\eta}\right]\}^{2}$$
이때, 저희의 목표는 $\sigma^{2}$를 최소화하는 것이고 $\sigma^{2}(x, y)$는 $w(x, y)$에 영향을 받기 때문에 $\frac{\partial \sigma^{2}(x, y)}{\partial w(x, y)} = 0$을 만족하는 $w(x, y)$을 찾으면 바로 풀리게 됩니다. 최종적으로 $w(x, y)$는 아래의 식으로 얻어지게 됩니다.
$$w(x, y) = \frac{\bar{g\eta} - \bar{g}\bar{\eta}}{\bar{\eta^{2}} - \bar{\eta}^{2}}$$
'image processing' 카테고리의 다른 글
| 디지털 영상 처리 - 선형 및 위치 불변 열화 함수 (0) | 2021.05.30 |
|---|---|
| 디지털 영상 처리 - 노이즈만 있을 때 복원하기(공간 필터링) : 적응 필터 구현 (0) | 2021.05.29 |
| 디지털 영상 처리 - 노이즈만 있을 때 복원하기(공간 필터링) : 평균 필터와 순서-통계 필터 구현 (0) | 2021.05.22 |
| 디지털 영상 처리 - 노이즈만 있을 때 복원하기(공간 필터링) : 적응 필터 (0) | 2021.05.12 |
| 디지털 영상 처리 - 노이즈만 있을 때 복원하기(공간 필터링) : 평균 필터와 순서-통계 필터 (1) | 2021.05.10 |
